基于短时傅里叶变换和深度卷积神经网络的直升机齿轮箱故障诊断方法
2022-06-09朱沁玥何海昊李泽东李志农谷士鹏
朱沁玥, 何海昊, 李 锋, 李泽东, 李志农,*, 谷士鹏, 程 娟
(1.无损检测技术教育部重点实验室(南昌航空大学),南昌 330063;2.中国飞行试验研究院,西安 710089)
0 引言
齿轮箱作为直升机传动系统重要组成部分,其运行状态关乎整个系统的健康运行。其一旦发生故障,将会给直升机带来巨大的安全隐患,可能造成经济损失或人员伤亡。因此,有必要对直升机的齿轮箱进行运维保障,研究齿轮箱故障诊断技术具有重要的理论研究价值和实际意义。由于齿轮的振动信号易于采集,对振动信号的处理和分析在齿轮箱的故障检测中发挥了重要的作用。然而,齿轮箱内部结构复杂, 故障信号可能混合了多种不同的振动信号[1],导致齿轮箱的故障检测难度加大。
为了实现对齿轮健康状态的保障,许多学者对齿轮诊断方法进行了研究。祝晓燕等[2]针对齿轮箱振动信号的非平稳特性和在现实条件下难以获得大量故障样本的实际情况,提出一种经验模态分解(Empirical Mode Decomposition, EMD)和支持向量机相结合的故障诊断方法;杨欢等[3]依据齿轮箱油液光铁谱数据,提出了一种基于BP神经网络的重型卡车齿轮箱故障诊断方法;毕静伟等[4]尝试将频率切片小波变换的时频分析方法应用到其故障诊断中。然而,这些研究都是针对普通齿轮的故障诊断,对处于复杂环境下的直升机齿轮还有待进一步的研究。因此,本研究以直升机齿轮为研究对象,进行智能诊断方法的研究。
深度卷积神经网络(Deep Convolution Neural Network,DCNN)作为人工智能中最经典的算法,在智能识别领域已经被广泛应用。卷积神经网络(CNN)是一种包含前向传播和反向传播的多层神经网络模型,具有强大的隐式特征提取能力,其通过多个卷积核对输入层的原始数据进行逐层提取得到特征,这些特征处于高维空间更易于分类识别。因此,CNN在齿轮箱故障诊断中也开始有了广泛的应用。饶雷等[5]提出了一种基于CNN和支持向量机(SVM)相结合的齿轮箱故障诊断模型;薛璇怡等[6]提出基于一维深度卷积神经网络(1D-CNN)的故障诊断方法,将原始信号直接输入到网络中进行诊断;张荣涛等[7]将DCNN与XGBoost算法相结合,建立故障诊断模型。上述研究中直接将原始振动信号输入神经网络的方法可以完成对齿轮箱内部某结构的故障诊断,但直升机齿轮箱内部结构复杂多样,采集到的振动信号往往是由故障信号、转动信号等多种信号混合而成的信号,且振动信号具有非平稳和非线性特点。因此,直接使用采集到的振动信号作为输入,使得网络难以提取到有效的特征,导致故障诊断模型无法满足实际需求。而短时傅里叶变换(Short-Time Fourier Transform,STFT)可以很好地针对非线性信号进行时频特征的提取,有效地提高时间分辨率。
本研究以直升机齿轮箱作为研究对象,提出一种基于短时傅里叶变换和深度卷积神经网络的故障诊断方法。该方法以单一振动信号为监测信号。首先,使用STFT将故障信号转换成时频图,在直升机齿轮箱上采集多种类型的故障,以构造大量的和多样性的样本,提高网络的鲁棒性。然后,将预处理后的样本作为CNN的输入,有监督地调整网络参数,以实现准确的齿轮箱故障诊断,并在实验中验证该方法的可行性,从而完成齿轮箱故障的诊断和其状态的监测。
1 基于短时傅里叶变换和深度卷积神经网络的故障诊断模型
1.1 短时傅里叶变换(STFT)
连续信号f(t)在完备正交信号空间内可展开为式(1):

式(1)即为傅里叶变换 (Fourier Transform)的定义式[8],用于将信号从时域到频域转换。成立的充分条件为在无限区间内f(t)绝对可积,即:
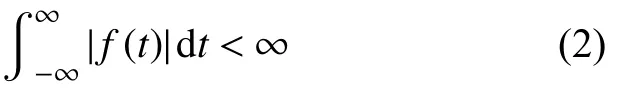
直升机齿轮箱内的振动信号并不平稳。非平稳信号由于波形特性没有规律,也没有频率的概念,需要对信号使用窗函数加窗截取限制变换的时间范围,让取样出来的信号在一个频率区间范围内,再对加窗后的信号分别进行傅里叶变换,最后对加窗变换完的信号进行叠加,即对信号进行STFT。STFT定义为:
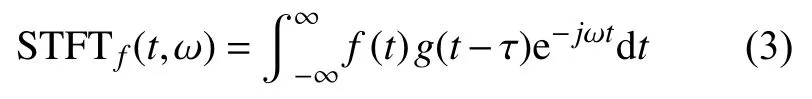
式中:f(t)为时域信号;g(t−τ)为窗函数;τ为窗函数的中心。经过STFT后得到的频率可看作该点的瞬时频率。
1.2 卷积神经网络(CNN)
CNN是一种模仿大脑视觉皮质、在图像处理与模式识别领域表现突出的神经网络。一个典型的CNN主要由输入层、卷积层、池化层、全连接层和输出层5部分组成(图1)[9]。

图1 卷积神经网络结构Fig.1 Structure of CNN
1)卷积层。卷积层 (Convolutional Layer)上进行的操作是卷积核与图像进行卷积。一个卷积层内可以有多个卷积核,每个卷积核负责从数据中提取一组指定的特征。特征提取完成后输出至下一层网络。卷积核w在范围为Mj的图像上卷积的数学表达式[10]为:
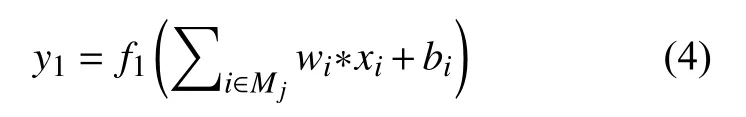
式中:y1表示第一层网络;xi表 示输入图像Mj中的第i个元素;∗表示卷积操作;bi为 偏移项;f1(·)为激活函数。
2)池化层。池化层 (Pool Layer)多接在卷积层之后,负责在减少数据数量同时保留有效的数据和提取到的特征,以减少参与运算数据的数量,便于建立更深层次的神经网络。最大池化层(Max Pooling)在每个n×n大小的区域内保留1个最大的数值而得到新的输出,最大池化的输出比输入在所有维度上均缩小为原来的
3)全连接层。全连接层 (Full Connect Layer)是完成特征分类的网络。全连接层将上层的网络提取到的所有特征进行分类汇总,再将分类的结果输出给下一层网络。其数学模型为[10]:
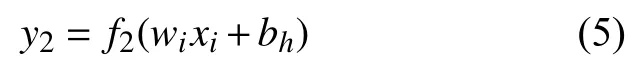
式中:f2为激活函数,常用SoftMax激活函数;bh为偏置;wi为权重。
CNN中多个卷积层和池化层构建多通道输入、多卷积核的网络,输入通过这些网络后得到多个输出矩阵,最后全部的输出矩阵在全连接层下在通道维度上合并。
1.3 批次归一化层
批次归一化 (Batch Normalization, BN)层可作为神经网络的一层,使用时多构成“卷积层−BN层−激活函数”的结构或构成“BN层−激活函数−卷积层”的结构。BN层进行的工作是对参数进行批量归一化,又称参数标准化,即将参数按照数据的均值和方差重映射到一定范围内。如将一组均值为µB,标准差为的数据 {x1,···,xm}映射到xi与之间的关系[10]为:
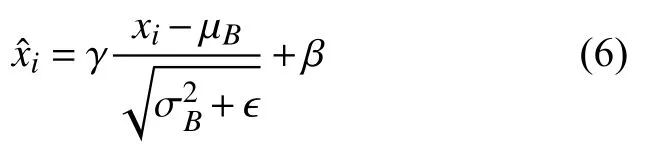
式中:ϵ是一个很小的数,为了防止分母为0;γ和β在反向传播中自动优化,即网络在正向传播时学习 γ和 β求出新的分布值;反向传播时链式求导求出γ和β。
BN层的作用是加快网络训练速度,避免导数过小导致梯度弥散对网络带来的网络训练速率减慢等不良影响,同时使训练前网络初始化时参数的选择更为自由。
2 基于STFT-DCNN的故障诊断流程
建立STFT-DCNN故障诊断模型的流程图如图2所示,具体步骤如下:

图2 本研究方法流程图Fig.2 Flowchart of the proposed method
1)获取原始振动信号。在齿轮箱上布置加速度传感器,采集振动信号。
2)预处理采集到的振动信号。为了更好地表达振动信号的特征,将振动信号通过STFT转化为时频图;裁剪时频图的非特征部分,即空白处和坐标等;由于生成的时频图大小不一,为了方便输入,将图片宽和高压缩成大小一样的形状,同时划分训练集和测试集。
3)构建DCNN网络。根据样本大小,初始化网络参数,确定网络超参数,如学习率、迭代次数、步长等。
4)训练DCNN网络。将步骤2中处理好的样本输入到网络中,通过前向传播求得网络输出与预期目标的误差,结合反向传播对网络的权重参数进行求导更新;判断网络的loss值是否收敛或者达到最大迭代次数,若收敛,则执行下一步,否则执行步骤3。
5)测试DCNN网络。利用测试样本对训练好的模型进行测试。根据准确度判断网络是否满足实际要求,满足需求则执行下一步,否则执行步骤2,重新修改样本划分比例和修改网络参数。
6)应用STFT-DCNN模型。训练好的网络模型可用于齿轮箱故障诊断。
3 实验与分析
3.1 样本集描述
研究所用行星齿轮箱(图3)包含3个行星齿轮,以太阳轮连接输入轴为结构输入件,行星齿轮为结构输出件。实验中对行星齿轮分别加工断齿和剥落两种故障类型,训练数据包含3种工况,无故障、断齿和剥落(图4)。使用传感器采集行星轮的振动信号,在采样频率为16.384 kHz、负载为0 MPa的条件下,对无故障、断齿和剥落3种齿轮状态下采样而得的振动信号生成时频图构建样本集。图5为行星齿轮箱上8个传感器测点的位置示意图。其中,测点1、5和2、6为正交位置,为了更好地监测齿轮同一时刻不同方向的信息;测点3、4为对立位置,为了获取更多信息;单测点7、8为简单的传感布置,以获取故障信息。

图3 齿轮箱实物Fig.3 Gearbox of helicopter

图4 齿轮不同故障Fig.4 Different fault types of gear
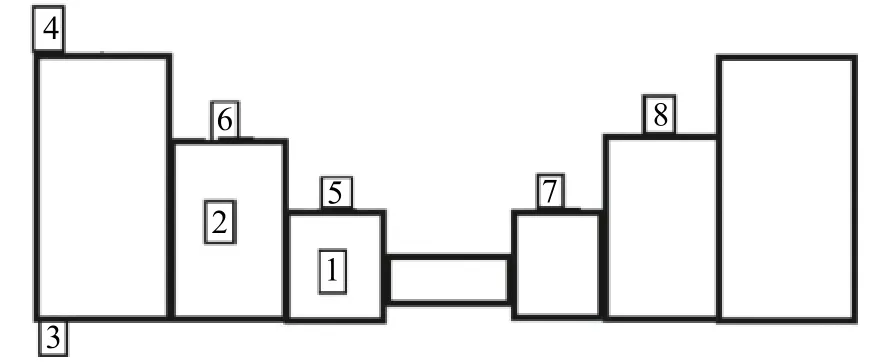
图5 传感器测点的位置Fig.5 Measuring points of sensor
每种故障信号样本数量为2976个,共计8928个样本。实验选取2048个样本点作为一组样本数据,按照实验步骤,利用STFT处理后得到时频图,将其裁剪、压缩变换成48×48的样本图,作为本文诊断模型的输入。故障所对应的编码、电机转速、控制器频率和样本数如表1所示。3种齿轮故障在同一种运行工况下的时频图(经STFT之后生成)如图6所示。
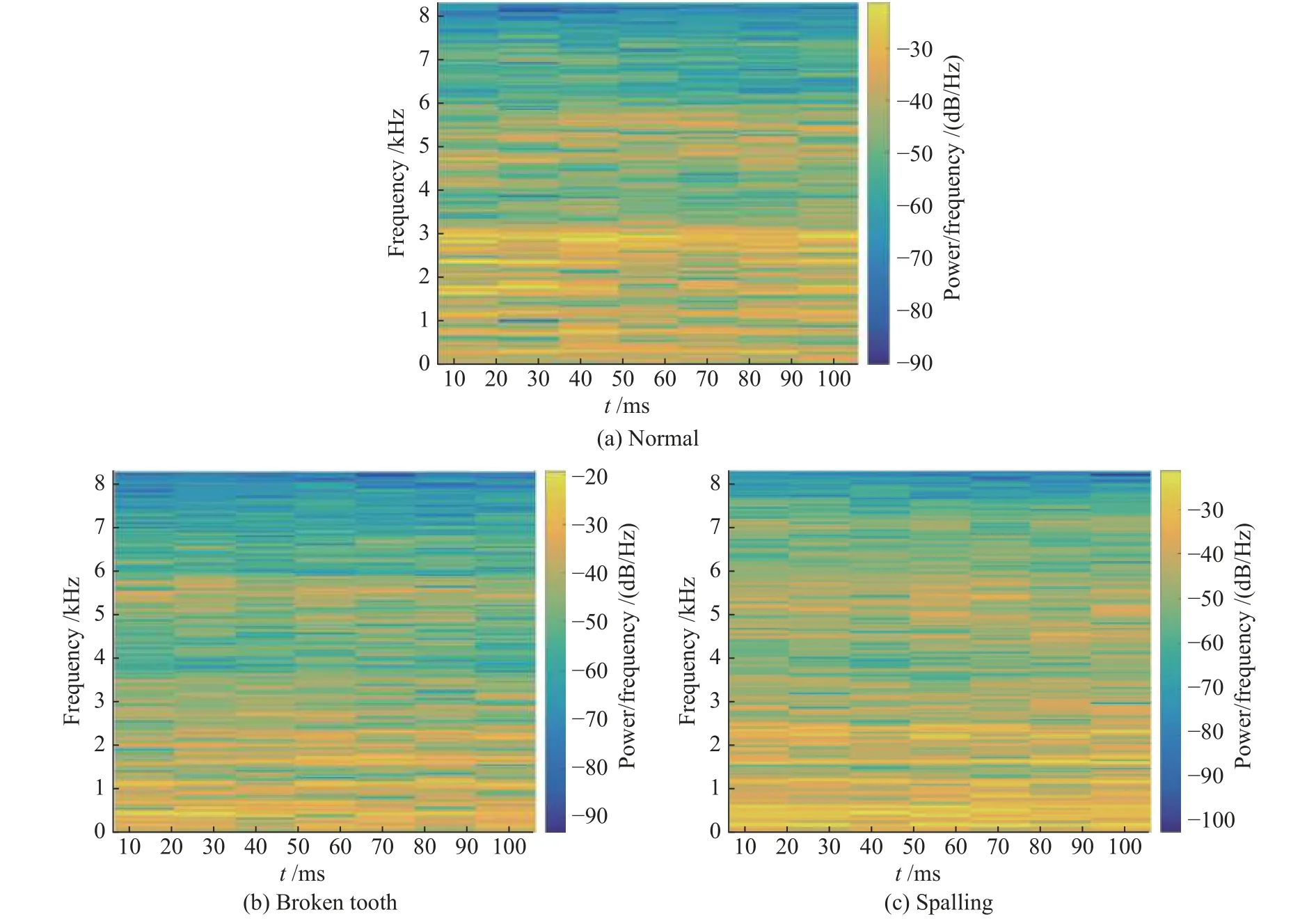
图6 不同类型故障的时频图Fig.6 Time-frequency diagram of different kinds of faults

表1 样本和齿轮箱信息Table 1 Information of specimen and gearbox
对于DCNN而言,训练集、测试集的比例划分不合理会导致模型准确率不佳,训练集数据过少会导致网络泛化能力差,测试集数量过少会导致测试结果不准确。为保证划分合理,对数据量在10 000以下的样本集,常见的做法是使用7:3划分训练数据和测试数据,或者6:2:2划分训练数据、验证数据和测试数据。在此实验中,样本按7:3的比例随机划分训练集和测试集,不设计验证集。表2为划分训练集与测试集大小后的相关信息。
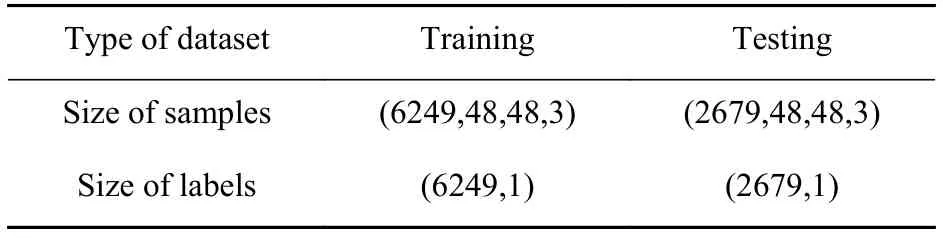
表2 训练集与测试集的数据大小Table 2 Size of training dataset and testing dataset
3.2 DCNN搭建
传统VGG13网络接受224×224的RGB图像输入,网络内部卷积层只使用步长为1的3×3卷积核,池化层使用步长为2的2×2窗口进行最大池化。本研究所使用的网络接受48×48的RGB图像输入,将传统VGG13模型内的“第一卷积层−第二卷积层−池化层”单元中加入BN层,改造成“第一卷积层−第二卷积层−BN层−池化层”单元加速网络收敛。输入先通过5个“第一卷积层−第二卷积层−BN层−池化层”单元,再通过3层全连接层输出3种分类结果。模型主要参数如表3所示。

表3 网络结构参数Table 3 Structure of network model
当设定好优化器后,网络在训练时将按照设定的梯度下降方案自动进行网络训练,更新权重和偏置,再自动完成前向传播的过程,自动将求得的误差反向传播,更改参数。损失函数是评价模型输出与目标一致的函数。本网络使用自适应矩估计优化器(Adam)调整参数,使用交叉熵损失(Categorical Cross Entropy) 函数作为损失函数进行反向传播。
3.3 参数设置
DCNN模型的超参数决定其网络性能,进而决定训练网络时花费的时间和网络预测时花费的时间。迭代回合(Epoch)过少,网络欠拟合;迭代回合过多,训练后期网络各指标变化不大,浪费时间和运算资源。学习率决定了网络反向传播过程中梯度下降算法更新参数的步长,学习率过低会导致网络收敛慢甚至陷入局部最优解,学习率过高会导致网络训练后期在最优点左右来回跳跃致使准确率波动幅度大。
最小训练量(Batch-size)是样本被分为的不同批次输入网络训练时每个批次的数量。最小训练量过小导致网络优化慢,最小训练量过大易导致网络仅能找到局部最优解而非全局最优。
实验超参数选取学习率为0.001,对连接层设置Dropout防止过拟合,其系数为0.4。模型每次最小训练量输入为128个样本,每迭代50次验证一次样本。网络超参数设置如表4所示。

表4 训练网络参数选择Table 4 Parameter selection of training network
3.4 结果分析
将划分好的训练集输送至网络中训练,完成一次前向传播和反向传播后计算损失函数;训练完成后使用测试集对网络进行测试,得出网络的实际准确率,模型的训练过程如图7所示。从图中可以看出,随着迭代次数的增加,模型的准确率不断提高,损失不断减小,但有个别回合的准确率突然变低,损失偏高。50次迭代结束后,网络模型最终测试集准确率达到了99.89%,测试集损失为0.037 7,这表明训练出的模型完全可用于判定直升机齿轮箱的故障,所建立的方法具有很高的准确率和稳定性。

图7 STFT-DCNN 的准确率曲线与损失函数曲线Fig.7 Accuracy curve and loss curve of the result of STFT-DCNN
3.5 模型对比
为了更好地验证短时傅里叶变换和深度卷积神经网络(STFT-DCNN)对齿轮箱故障诊断的分类效果,选用Hilbert-Huang变换和深度卷积神经网络(HHT-DCNN)、小波变换和深度卷积神经网络(WT-DCNN)两种不同的诊断分类方法来进行对比研究。
Hilbert-Huang变换是一种常用的信号时频分析技术。于德介等[11]将Hilbert-Huang变换引入齿轮故障诊断中,将局部Hilbert能量谱与支持向量机结合实现故障模式识别。对于Hilbert-Huang变换提取特征结合深度卷积神经网络这一诊断方法[12],其基本原理是对齿轮振动信号采用EMD方法有效地将各个频率族分离,而局部Hilbert能量谱可以反映齿轮振动信号的能量随时间和频率的分布情况,从而提取出齿轮振动信号的故障信息。但在本研究中,直接输入局部Hilbert能量谱时域图于深度卷积神经网络中训练网络得到的网络分类准确率只有54.55%,识别结果并不令人满意。图8分别为Hilbert-Huang变换提取特征和DCNN的准确率曲线和损失函数曲线。
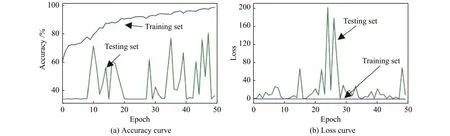
图8 HHT-DCNN 准确率曲线与损失函数曲线Fig.8 Accuracy curve and loss curve of the result of HHT-DCNN
小波变换(Wavelet Transform, WT)也是进行信号时频分析和处理的方法,它通过小波基的尺度变换,提供了一个动态变化的“时间−频率”窗口。孙俊伟[13]采用了小波包对齿轮箱故障进行故障诊断,从而认为用小波包分析对准确识别冲击信号十分有效。在此,应用小波变换和深度卷积神经网络(WT-DCNN)这一诊断方法[14-16],先将样本进行小波转化为时频图,再输入深度卷积神经网络中进行训练,得到的准确率曲线和损失函数曲线如图9所示。WT-DCNN的准确率达到88.29%,相比于STFT-DCNN还是有一定差距。
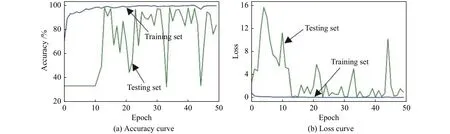
图9 WT-DCNN 的准确率曲线和损失函数曲线Fig.9 Accuracy curve and loss curve of the result of WT-DCNN
4 结论
1)将STFT-DCNN方法应用于直升机齿轮箱故障诊断,可以有效识别直升机齿轮箱的正常、断齿和剥落故障,准确率超过99%。该方法有效构建了故障特征与不同故障类别的关系,降低了信号处理后寻找故障特征频率的需求,提高了故障诊断的智能化。
2)STFT-DCNN方法与 HHT-DCNN和 WTDCNN采用不同的信号预处理方式,通过对比实验可知,经STFT对原始信号的时频变换后,故障诊断准确率更高。
