导波模态类型对锚固锚杆无损检测的影响
2021-09-14牛潘宇张昌锁赵金昌李鹏
牛潘宇, 张昌锁, 赵金昌, 李鹏
(太原理工大学 矿业工程学院,山西,太原 030024)
超声导波无损检测技术可以在不破坏锚固结构的条件下实现锚固质量的检测,是一种方便、快捷、高效的锚固质量检测方法. 应用这种技术进行检测时,只需要在锚固好的锚杆端头激发一定频率的超声导波,然后在同一个位置用信号接收器接收锚杆底端的反射信号,通过分析这些信号就可以得到所测锚固结构的质量情况[1-2]. 但是现有研究表明,在锚固结构中传播的超声导波由于存在严重的能量泄漏而无法得到锚杆底端的反射信号[3-4]. 因此,研究锚固结构中超声导波的传播规律,获得衰减小、适用于无损检测的超声导波是一项极其重要的工作.
超声导波存在纵向模态、扭转模态和弯曲模态3种形式[5]. 应用超声导波检测管道结构的缺陷时,不同模态类型的导波对缺陷的敏感程度不同. 纵向模态对周向缺陷更敏感,对轴向缺陷识别不准确,而扭转模态可以很好地识别这两种方向的缺陷[6]. 应用超声导波检测锚杆结构的锚固质量时,通常以纵向模态为研究对象[7],通过理论计算、数值模拟和实验测试的方式研究锚杆结构中的导波传播规律,从而获得衰减小并能用于现场检测的最优激发波[4, 8-9],或者在纵向模态导波的基础上寻找能够激发单一模态的导波[10]. 与纵向模态相比,锚固结构中扭转模态和弯曲模态导波传播特性的研究相对较少. 由于扭转模态对轴向缺陷的敏感性和可以有效识别浆体属性变化的特性[11-12]使得研究扭转模态的导波传播规律也很重要. 而对于弯曲模态,不仅理论研究很少,而且由于激发波的生成比较困难也很少进行相关的实验测试[13].
因此,本文以锚杆直接锚固于无限岩体的双层锚固结构为波导结构,通过理论计算和数值模拟两种方法研究纵向模态、扭转模态和弯曲模态超声导波的传播规律,从而指导无损检测中测试波的选择.
1 不同模态超声导波的频散规律
1.1 锚固锚杆结构理论模型的建立
工程中的锚固锚杆结构可以看作是由锚杆、锚固剂和无限岩体构成的三层圆柱体模型. 对于锚固剂为混凝土的砂浆锚杆,由于混凝土达到终凝条件后,它的材料参数与岩体的相似,在研究中可以将混凝土和岩体看作一种材料,共同作为锚固锚杆的锚固体. 因此对于砂浆锚杆,它的理论模型可以简化为锚杆直接锚固于无限岩体的双层圆柱体模型,如图1所示. 根据工程实际,进行理论计算的锚杆直径为20 mm,岩体在径向方向无限大,对应的材料参数如表1所示.

图1 砂浆锚杆的双层圆柱体模型Fig.1 Two-layer infinite rock mass model of grouting rock bolt
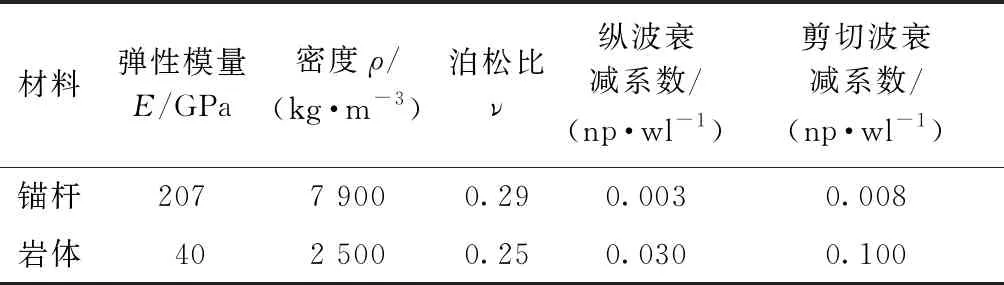
表1 砂浆锚杆的材料参数Tab.1 Material parameters of grouting rock bolts
1.2 频散方程的建立
本文应用全局矩阵法[14]建立超声导波在多层圆柱体波导结构中传播的频散方程. 根据砂浆锚杆理论模型的层数和边界条件,可以用式(1)表示频散方程的通用表达式,式中矩阵D是与模型材料参数,径向位置r,周向阶数n,以及贝赛尔函数相关的6×6维矩阵,Dij是矩阵D的一项,其具体计算公式参考文献[14].
根据式(1)可以推导得到纵向模态、扭转模态和弯曲模态超声导波在砂浆锚杆中的频散方程. 因为纵向模态和扭转模态都是轴对称模态,对应的周向阶数n为0,所以将n=0代入式(1),通过整理就可以得到纵向模态和扭转模态的频散方程,用式(2)和式(3)表示. 对于弯曲模态,其周向阶数n可以为任意正整数[5],而本文只研究1阶弯曲模态超声导波的频散规律,所以将n=1代入式(1)就得到了1阶弯曲模态的频散方程. 因此,砂浆锚杆结构中纵向模态超声导波对应的频散方程是用4×4维行列式表示的等式,扭转模态超声导波对应的频散方程是用2×2维行列式表示的等式,弯曲模态超声导波对应的频散方程是用6×6维行列式表示的等式.
(1)
(2)
(3)
1.3 频散曲线的求解与分析
本文根据LOWE[15]提出的高效求解频散方程的算法,应用Matlab软件编写了一套计算频散方程的程序,然后对不同模态的频散方程进行计算.
1.3.1纵向模态超声导波的频散规律
将模型的材料参数和模型尺寸代入式(2),计算得到纵向模态导波的衰减频散曲线如图2(a)所示,相应的相速度频散曲线如图2(b)所示. 图2(a)中,在频率小于2.5 MHz衰减小于250 dB/m的范围内,存在12条衰减频散曲线,按照曲线截止频率从小到大的顺序将它们分别编号为L(0,1)~L(0,12).
根据衰减曲线的变化形式,可以将图2(a)中的曲线分为三类:第一类是L(0,1)模态曲线,它的初始导波频率接近0,对应的衰减是有限值(200 dB/m),并且曲线存在一个极小值点;第二类是与L(0,7)变化形式相似的模态曲线,这些曲线的衰减随着频率的增加从无限大迅速减小,然后上下波动并逐渐趋于平缓,因此曲线上存在多个极小值点,并且衰减相对较小;第三类是剩余的模态曲线,这些曲线的变化形式与第一类的相似,但初始导波的衰减是无限大而不是有限数值.
同样这些模态对应的相速度频散曲线也可以分为三类,如图2(b):第一类的L(0,1)模态曲线的初始相速度是有限值,并且相速度随着频率的增加先增后减,最后趋于锚杆的剪切波速;第二类的L(0,7)模态曲线的初始相速度从无限大值迅速减小,然后缓慢变化并逐渐趋近于锚杆的纵向波速;第三类的其他模态曲线的初始相速度也是从无限大迅速减小,但随着频率的增加,相速度最终逐渐趋近于锚杆的剪切波速.
由图2(a)的衰减频散曲线可知,在小于0.5 MHz的低频范围内,L(0,1)~L(0,4)模态的所有导波衰减都大于100 dB/m;而高频范围内存在衰减较小的超声导波,其中L(0,7)模态曲线上所有极小值的导波衰减在20~44 dB/m范围内,并且这些导波的衰减值随着频率的增加在逐渐减小. 因此,只有高频范围内L(0,7)模态曲线的衰减极小值点才有可能作为无损检测中的最优测试波. 图2(a)中,点A是L(0,6)模态曲线的极小值点,点B~F分别为L(0,7)模态曲线上的极小值点,这些导波将作为数值模拟中的激发波.

图2 纵向模态导波的频散曲线Fig.2 Dispersion curves of longitudinal mode guided waves
1.3.2扭转模态超声导波的频散规律
计算式(3)得到扭转模态的衰减频散曲线如图3(a)所示,相应的相速度频散曲线如图3(b)所示. 在小于2.5 MHz的频率范围内,根据模态曲线的截止频率对曲线以T(0,m)(m=1,2,3……)的形式编号.
在扭转模态的衰减频散曲线图中,可以看到所有曲线的变化形式都相同:随着频率的增加,模态的衰减都是从无限大迅速减小到180 dB/m附近,然后上下缓慢波动变化. 对于扭转模态的相速度频散曲线,它的变化形式同样很简单:随着频率的增长,相速度都是从无限大快速减小并且逐渐趋近于导波在锚杆中的剪切波速.
与纵向模态的衰减频散曲线相比,扭转模态的衰减曲线虽然没有明显的极值点并且曲线更加平滑,但是所有导波的衰减都大于180 dB/m,由于实际测试中的信号放大器的最大增益只有80 dB左右,所以扭转模态的超声导波因衰减太大而无法得到锚杆底端的反射信号.
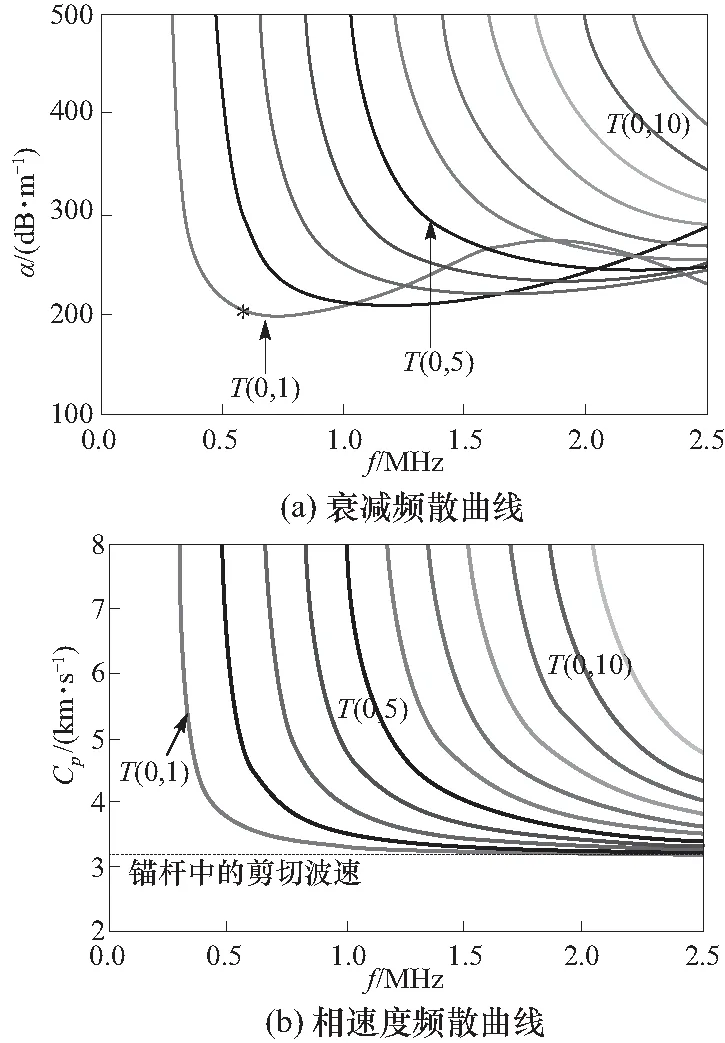
图3 扭转模态导波的频散曲线Fig.3 Dispersion curves of torsional mode guided waves
1.3.3弯曲模态超声导波的频散规律
将n=1代入式(1)得到1阶弯曲模态的频散方程,通过计算得到的频散曲线如图4所示. 由于弯曲模态的频散方程比纵向模态和扭转模态的频散方程都复杂,所以在相同的频率范围内,弯曲模态的频散曲线数目更多,曲线的变化形式也更加复杂. 在图4(a)的弯曲模态衰减频散曲线图中,一部分曲线的变化形式与纵向模态的相似:随着频率的增长曲线上的衰减都是大幅度波动,形成了明显的极值点,例如F(1,2)和F(1,4)等曲线;另一部分曲线与扭转模态的相似,随着频率的增加它们的衰减先迅速减小然后缓慢上下波动,例如F(1,1)和F(1,5)等曲线. 同样在图4(b)中,弯曲模态的相速度频散曲线也可以对应于纵向和扭转模态的相速度变化形式.
参考纵向模态超声导波的衰减规律,弯曲模态在高频范围内也存在衰减相对较小的超声导波,但是这些导波的衰减都大于50 dB/m,例如F(1,10)曲线的极小值点. 与另外两种模态的频散方程相比弯曲模态的维数更高,相应的波结构也会更复杂,从而使得弯曲模态超声导波的激发相对困难. 因此弯曲模态由于衰减大、不易激发等缺点而不作为锚固结构的测试波.

图4 弯曲模态导波的频散曲线Fig.4 Dispersion curves of flexural mode guided waves
2 数值模拟
应用ANSYS有限元软件建立砂浆锚杆结构的数值模型时,通常用小直径的实验试件模拟实际情况中具有无限外径的砂浆锚杆结构. 由于低频超声导波的波长与锚杆的直径相近,使得泄漏到锚固体中的低频导波在实验试件的侧面边界发生反射,最终影响有用信号的识别[16]. 而高频超声导波在泄漏到锚固体后会迅速衰减,因此受到实验试件侧面边界的影响相对较小[3].
进行数值模拟计算研究超声导波的传播规律时,首先改变数值模型外径的大小,研究低频纵向模态超声导波与实验模型侧面边界的作用关系;然后以文献[4]中外径为160 mm的实验试件为研究对象,研究导波模态类型对高频超声导波衰减的影响情况.
2.1 纵向模态超声导波的数值模拟
2.1.1纵向模态超声导波数值模型的建立
用于数值模拟的锚固锚杆结构中,锚杆的直径为20 mm,长度为800 mm,锚固方式为全锚锚固. 模拟纵向模态超声导波的传播时,可以将锚固锚杆结构简化为平面轴对称模型. 图5是包含锚杆激发端的锚固锚杆数值模型放大图. 模型中,锚杆和锚固体的单元类型都是PLANE162,单元尺寸满足一个波长内包含15~20个单元的条件. 计算中,激励信号用加汉宁窗的正弦函数表示,并以力荷载的形式沿轴向方向加载到锚杆端头的所有节点上. 图6是频率为0.90 MHz的激励信号.

图5 砂浆锚杆的平面数值模型图Fig.5 Schematic diagram of the plane numerical model of grouting rock bolt

图6 频率为0.90 MHz的激励信号Fig.6 Excitation signal with wave frequency of 0.90 MHz
2.1.2低频纵向模态超声导波的数值模拟
将图2(a)中L(0,1)模态衰减频散曲线的最小值点作为激发波进行数值模拟,分别计算低频超声导波在外径为1 ~4 m的锚固锚杆数值模型中的传播情况,从而探究低频超声导波受实验模型侧面边界的影响情况. 数值模拟中激发波的频率为70 kHz,对应的理论衰减为108 dB/m. 在不同模型锚杆激发端接收的时域波形图如图7(a)所示,在锚杆底端接收的时域波形图如图7(b)所示.
从图7的结果可以看到,无论是锚杆激发端还是锚杆底端的时域波形图,都存在一组波包,它们的接收时间与模型的外径为线性关系,所以这些信号都是经过模型侧面边界反射得到的. 由于所有模型的轴向长度都是800 mm,所以图7中波形和接收时间不随模型外径变化的波包就是沿锚杆轴向传播的有用信号,即图中虚线框内的波包.
将图7(a)中模型外径为1 m的波形图与其它模型的波形图比较可以发现,沿锚杆轴向传播的有用信号被模型侧面边界的反射信号覆盖,因而无法直接判断锚杆底端反射信号的位置和波形情况. 除此之外,在所有的波形图中,侧面反射信号的强度远远大于有用信号的强度. 因此,低频超声导波在外径只有160 mm左右的实验试件中传播时,确实会受到模型侧面边界的严重干扰,因而无法模拟导波的真实传播情况.
2.1.3高频纵向模态超声导波的数值模拟
选择图2(a)中高频范围的衰减极小值点作为激发波进行数值模拟,这些导波的编号、频率和理论衰减如表2所示.

图7 频率为70 kHz的纵向模态导波在不同径向尺寸锚固锚杆中的时域波形图Fig.7 Time-domain waveforms of longitudinal mode guided waves with a frequency of 70 kHz in grouting rock bolt of different radial sizes

表2 高频纵向模态超声导波的参数
将这些高频超声导波输入到外径为160 mm的砂浆锚杆数值模型中,然后在锚杆激发端接收信号. 为了使不同频率导波的时域波形图之间具有可比性,将激发波的相对幅值设置为1,然后再将所有信号放大1 000倍得到图8所示的结果. 从图中可以看到不同频率导波的首个锚杆底端反射信号波形非常清晰(图中虚线框内的波包);而在导波频率分别为0.90,1.09 和1.28 MHz的3个波形图中,锚杆底端的二次反射波幅值非常小,几乎无法识别,说明这些导波会在砂浆锚杆中快速衰减;但是在f≥1.47 MHz的其他波形图中,都存在2个以上锚杆底端反射信号,并且这些信号的波形都很清晰. 因此,根据图8可知,在0.90~1.85 MHz的频率范围内,更高频率的纵向模态超声导波由于衰减相对较小,可以在锚固结构中传播更远的距离,这也与对应的理论计算规律完全一致.
为了定性分析这些导波在实验模型中的衰减情况,以图8的首个锚杆底端反射信号和二次反射信号为计算波包,根据式(4)计算数值模拟中导波的衰减大小,并将结果列在表2中.
(4)
式中:a为数值模拟衰减;A1为首波波幅;A2为二次反射波波幅;L为模型的轴向长度.
将表2中纵向模态超声导波的理论衰减和数值模拟衰减分别与频率的关系绘制在图9中. 可以看到,随着频率的增长,纵向模态超声导波的这两种衰减都是以递减的趋势变化,说明了本文理论计算结果的正确性,同时也说明高频纵向模态超声导波由于衰减相对较小可以用于锚固锚杆的无损检测.

图8 高频纵向模态超声导波的数值模拟时域波形图Fig.8 Time-domain waveform diagram of numerical simulation of high-frequency longitudinal mode ultrasonic guided waves
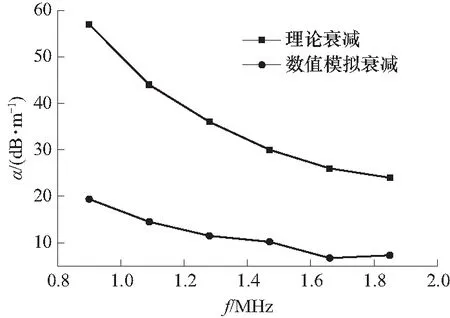
图9 纵向模态导波的频率-衰减关系图Fig.9 Relationship of frequency and attenuation of longitudinal guided waves
2.2 扭转模态超声导波的数值模拟
2.2.1扭转模态超声导波数值模型的建立
由于扭转模态超声导波的加载方向与导波的传播方向垂直,所以需要用三维圆柱体模型模拟锚固锚杆结构. 图10(a)是锚固锚杆端面的网格划分情况,采用过渡网格的方式对锚杆单元进行加密,既保证了结果的正确性,又减少了模型的总单元数.
数值模拟计算中,锚固结构的尺寸和材料参数均与纵向模态的相同. 扭转模态导波仍然用加汉宁窗的正弦函数表示,并以周向力荷载的方式加载到锚杆端头外围的所有节点上[11]. 图10(b)是周向力荷载和过渡网格.

图10 砂浆锚杆的空间数值模型图Fig.10 Schematic diagram of the space numerical model of grouting rock bolt
由于扭转模态和弯曲模态超声导波的理论衰减比纵向模态的大很多,只在锚杆端头接收波形信号无法真实反映导波的传播过程. 所以,对扭转模态和弯曲模态超声导波进行数值模拟时,在锚杆轴向方向等距选取5个节点接收的导波波形图进行分析,这些节点的位置如图11所示.

图11 数值模拟中信号接收点的位置Fig.11 Location of monitoring points in numerical simulation
2.2.2扭转模态超声导波的数值模拟与结果分析
图3(a)中扭转模态衰减频散曲线的所有极小值点的衰减都在180 dB/m左右,由于数值模型中单元数目随激发波频率的增加显著增多,所以根据图3(a)选择T(0,1)模态曲线上600 kHz对应的导波作为激发波进行扭转模态的数值模拟计算,相应的理论衰减为190 dB/m.
图12是M1~M5这5个节点接收的时域波形图. 观察这几个波形图可以发现,频率为600 kHz的扭转模态导波传播到锚杆总长的1/4时,导波的幅值衰减了33万倍,并且到达锚杆总长的1/2时,导波的波形已经无法识别. 这样的结果说明600 kHz的扭转模态导波在锚固锚杆结构中的衰减非常大,这与理论计算的衰减情况非常吻合.

图12 扭转模态导波的数值模拟结果(600 kHz)Fig.12 Numerical simulation results of torsional mode guided waves (600 kHz)
2.3 弯曲模态超声导波的数值模拟
2.3.1弯曲模态超声导波数值模型的建立
弯曲模态超声导波的数值模拟模型同样采用图10(a)所示的三维圆柱体模型. 计算中,弯曲导波以竖向力荷载的方式加载到锚杆激发端外围的所有节点上[17],如图13所示.
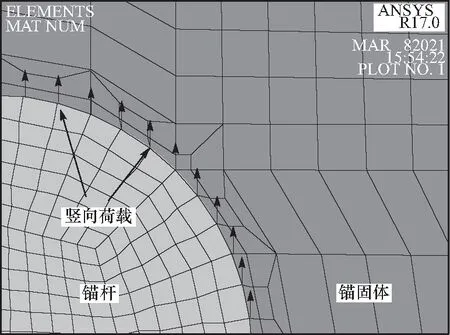
图13 弯曲模态导波的竖向荷载Fig.13 Vertical load for flexural mode guided waves
2.3.2弯曲模态超声导波的数值模拟与结果分析
根据图4(a)弯曲模态的衰减频散曲线,选择F(1,4)模态的衰减极小值点作为激发波进行数值模拟,其中导波的频率为800 kHz,对应的理论衰减为145 dB/m. 计算得到的波形图如图14所示.
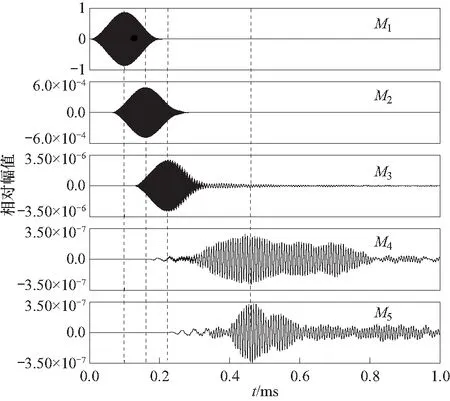
图14 弯曲模态导波的数值模拟结果(800 kHz)Fig.14 Numerical simulation results of flexural mode guided waves (800 kHz)
从图中的结果可以看到,频率为800 kHz的弯曲导波可以传播到锚杆底端,但是比较各个波包之间的幅值变化情况发现,弯曲导波在传播的初期迅速衰减,然后随着距离的增加,衰减幅度逐渐减缓. 根据M1和M5节点接收的波形图计算得到弯曲导波的平均衰减值为161 dB/m,表明了弯曲导波的衰减也很大,这与理论计算的衰减情况也吻合.
3 结 论
本文用锚杆直接锚固于无限岩体的双层圆柱体模型模拟现场中的砂浆锚杆. 通过理论计算和数值模拟的方式对纵向模态、扭转模态和弯曲模态超声导波在砂浆锚杆中传播的频域和时域规律进行计算与分析,得到了以下结论.
① 计算3种模态在0~2.5 MHz范围内的频散曲线:纵向模态的衰减频散曲线上存在明显的极小值点,其中频率小于0.5 MHz的低频导波衰减都大于100 dB/m,而高频范围内存在衰减为20~44 dB/m的超声导波. 对于扭转模态,虽然衰减频散曲线的变化形式简单并且曲线上没有明显的极值点,但是所有超声导波的衰减都大于180 dB/m. 对于弯曲模态,不仅所有导波衰减都大于50 dB/m,而且因为波结构复杂而不易激发. 因此,高频范围的纵向模态超声导波由于衰减小、易激发等优点可以作为砂浆锚杆无损检测的首选对象.
② 将纵向模态L(0,1)衰减频散曲线的极小值(70 kHz)作为激发波输入到不同外径大小的砂浆锚杆数值模型中,得到的时域波形结果表明低频超声导波确实会在实验模型的侧面边界发生反射并且严重干扰沿锚杆轴向传播的有用信号的识别.
③ 对0. 90~1. 85 MHz范围内的纵向模态导波进行数值模拟,得到的衰减规律与理论计算的衰减情况相同,都是随着频率的增加在逐渐减小.
④ 对扭转模态和弯曲模态超声导波在锚固锚杆中的传播也进行了数值模拟,得到的结果表明两种模态的导波衰减确实很大,与相应的理论计算结果吻合. 因此,扭转模态和弯曲模态超声导波无法用于锚固锚杆结构的无损检测.
