盾构隧道壁后注浆浆液时变性对围岩应力与变形的影响机理

周 中，胡江锋，刘撞撞，鲁四平

（中南大学 土木工程学院，湖南 长沙 410075）

近年来盾构机越来越广泛的运用到隧道施工，由于衬砌管片是在盾壳内部完成拼装，衬砌管片与盾尾分离后，围岩和衬砌之间会形成一定厚度的盾尾间隙，为了保证围岩和隧道衬砌的稳定性，需要及时的注浆填充此部分间隙，并施加一定大小的注浆压力，控制围岩的应力释放和变形以及隧道衬砌受力和轴线位置的合理性。其中壁后注浆浆液在围岩中的渗透扩散及渗透压力对围岩的影响性分析直接影响到壁后注浆的效果。

随着盾构技术的不断发展，国内外学者对盾构施工壁后注浆工艺进行了全方面的研究。Bezuijen等[1]、黄宏伟等[2]分别通过现场注浆压力测试试验和探地雷达探测试验探究盾构隧道壁后注浆效果；白云等[3]、袁小会等[4]分别借助牛顿流体、宾汉姆流体模型建立盾尾间隙内浆液压力的空间分布模型，得到仅考虑充填注浆情况下的浆液扩散规律；Yukinori等[5]基于物理模型试验的方法探究注浆压力、土的密实度对土体压力的影响；汪优等[6]基于流固耦合的渗流计算模型，研究注浆参数对渗流场的影响；张志强等[7]建立三维有限元模型模拟盾构掘进，提出控制同步注浆以降低隧道围岩及管片变形的措施；Ezzeldine[8]、Qiao 等[9]基于有限元程序，研究同步注浆对隧道衬砌、围岩变形及地面沉降的影响；叶飞等[10−12]引入等效孔隙率的概念，利用浆液柱形扩散模型计算注浆过程中浆液对管片产生的压力，并在之后的研究中考虑浆液的空间效应及浆液与土体的相互作用，建立了盾构隧道壁后注浆渗透扩散模型；梁禹等[13]考虑到因浆液黏度时变性而引起的地层渗透系数的改变，推导出适用性更强的浆体固结变形方程和浆液压力消散方程，分析了浆液沿管片外壁分布规律；张伟杰[14]、李志明等[15]研究了注浆对土体的加固机理，并通过试验得到注浆压力、浆液参数和注浆速率对土体加固范围的影响规律；苟长飞等[16]、王朝亮等[17]建立了柱形孔压滤扩散模型，通过对围岩孔隙水压力的分析，得到了浆液扩散规律和土体有效应力的关系；杨志全等[18]、刘健等[19]考虑浆液的黏度时变性，建立新的理论模型分析浆液黏度时变性和注浆压力大小对隧道衬砌结构受力的影响。曹胜语等[20]基于柱面扩散理论，推导考虑或不考虑黏度时变性情况下注浆扩散半径和注浆压力计算式，研究管片压力变化规律。然而目前国内外学者对盾构隧道壁后注浆的研究多停留在衬砌管片受力方面，对浆液向围岩中渗透扩散对围岩的影响方面研究不足。

本文围绕盾构壁后注浆浆液在围岩内的渗透扩散开展研究，建立考虑以及不考虑黏度时变性的浆液渗透扩散方程，推导出渗透压力对围岩内力与变形影响的计算表达式，并结合长沙地铁4号线盾构隧道施工实例分析盾构隧道壁后注浆对围岩稳定性的影响。

1 渗透扩散理论

盾构隧道壁后注浆一般根据注浆孔位置的不同分为2种：管片注浆和盾尾注浆。本文不考虑盾壳的影响，对管片注浆时的浆液扩散进行研究。当注浆压力较小时，壁后注浆主要以充填注浆为主，起填充盾尾空隙和传递荷载的作用，进而控制围岩的应力释放，控制地层变形；当注浆压力较大时，填充区的浆液压力和开挖洞室水压力会形成水头差迫使浆液向围岩中渗透扩散，在渗透压力的作用下，围岩产生径向压缩变形。

1.1 基本假设及适用范围

（1）本文理论是在壁后注浆为渗透注浆的基础上进行研究分析，隧道围岩条件符合注浆发生渗透扩散要求；

（2）假设围岩为均质各向同性，侧压力系数λ=1，在渗透压力作用下只发生弹性变形；

（3）设注浆浆液在围岩中扩散过程为均匀圆筒形扩散，且符合达西定律；

（4）设注浆压力和水压力沿隧道周围均匀分布。

本文提出的盾构隧道壁后注浆浆液在围岩中的扩散理论模型适用于土体自稳性较好、深埋盾构隧道的单液浆管片注浆。

1.2 渗透扩散方程

壁后注浆浆液在围岩内渗透扩散模型如图1所示。图中：x轴为沿隧道断面中心的水平方向，y轴为沿隧道断面中心的竖直方向；浆液在扩散区内圆半径（填充区外圆半径）r0处，浆液压力为P0；扩散区外圆半径r1处，浆液压力为Pw；在扩散区内部的任意扩散半径r处，浆液压力为Pr。

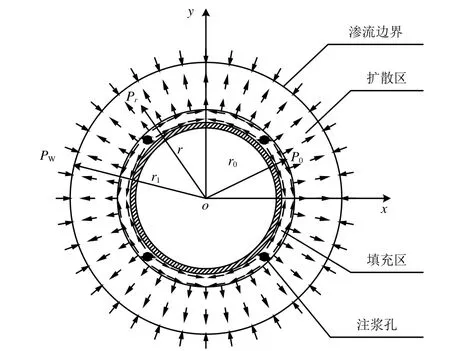
图1 浆液渗透扩散模型

由于填充区的浆液压力和开挖洞室水压力存在水头高度差dh，注浆浆液会向围岩中发生径向渗透扩散，扩散路径为dr，考虑到在渗透压力的作用下渗透半径增大，根据达西定律有

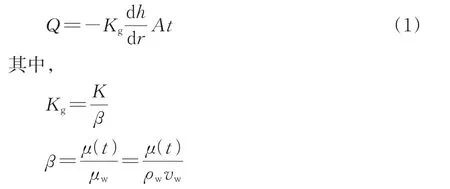
式中：Q为注浆浆液的扩散量；A为渗透扩散断面面积；t为注浆时间；Kg为注浆浆液在土层中的渗透系数；K为水在围岩土体中的渗透系数；β为浆液黏度与水的黏度比；μ（t）和μw分别为浆液、水的黏度；ρw为水的密度；vw为水的运动黏滞性系数。

2 围岩应力与变形计算方程

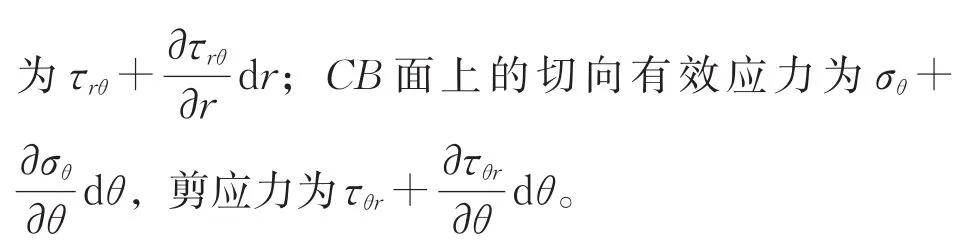
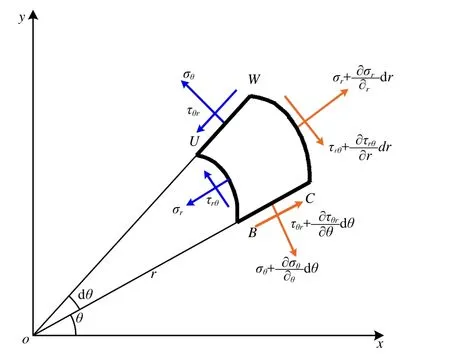
图2 壁后围岩微元体受力示意图

3 浆液时变性对围岩的影响

依托长沙地铁4号线盾构隧道施工实例，结合现场施工参数，利用Matlab软件对本文所建立的渗透扩散理论模型进行计算分析，讨论不同注浆参数对围岩的影响，提出壁后注浆对围岩的影响机理。注浆方式为四孔同步注浆，注浆压力300 kPa，浆液水灰比为0.8，属于宾汉姆流体，盾构隧道立面图如图3所示。

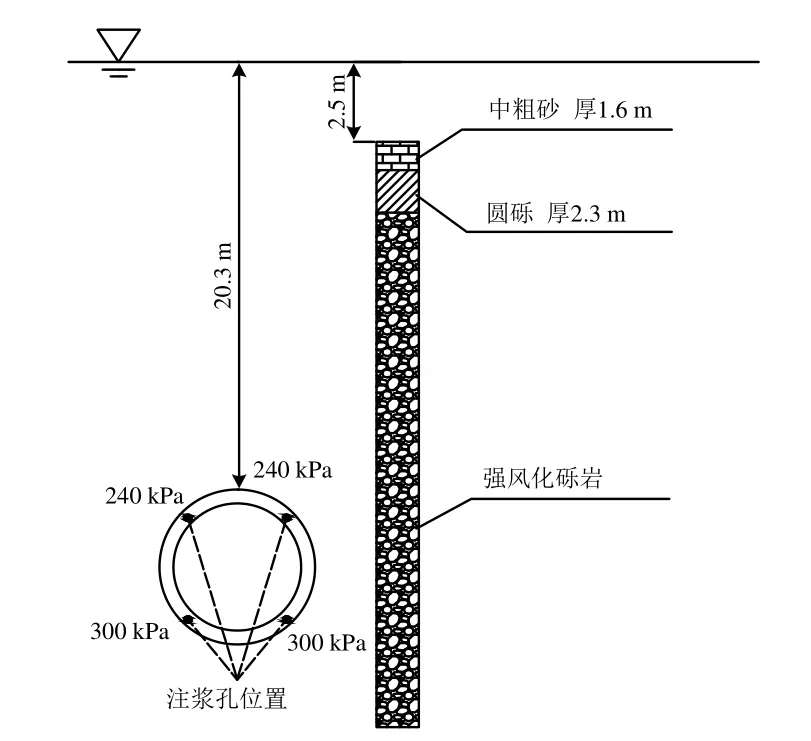
图3 长沙地铁4号线盾构隧道立面示意图

该监测断面处江水水深2.5 m，盾构隧道埋深17.8 m，隧道全处于强风化砾岩中。盾壳半径r'=3.14 m，管片外半径R=3.0 m，管片宽度B=1.5 m，推进距离dvt设为1个管片宽度，盾构机掘进速度v=2.6 m·h−1，注浆时间t=30 min。水头高度h0=20 m，原岩应力σ0=0.2 MPa。注浆浆液初始黏度值μ0=19.9 Pa·s，浆液黏度时变系数a=0.014 11 s−1。围岩的材料参数：弹性模量E=100 MPa，泊松比μ=0.25，孔隙率n=0.15，渗透系数K=5×10−6m·s−1，黏聚力c=50 kPa，内摩擦角φ=37°。

3.1 浆液扩散半径

长沙地铁4号线盾构隧道开挖半径为3.14 m，壁后注浆施工过程中，设注浆时间为30 min，分别取注浆压力为0.2～1.2 MPa，根据式（8）和式（9），代入现场施工参数，利用Matlab软件编程计算得到对应注浆压力作用下浆液的扩散半径，如图4所示。同样，设注浆压力为0.3 MPa，分别取注浆时间为0～40 min，得到对应注浆时间下浆液的扩散半径，如图5所示。

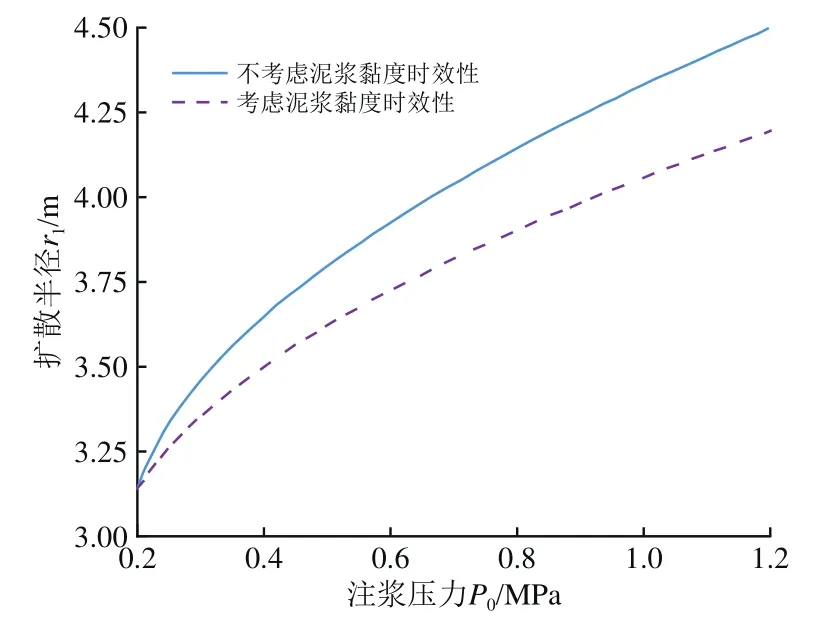
图4 浆液扩散半径随注浆压力变化曲线

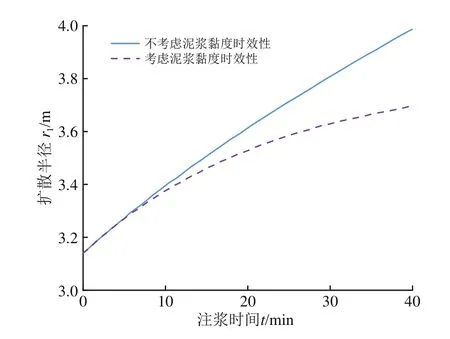
图5 浆液扩散半径随注浆时间变化曲线

由图4和图5可以看出：壁后注浆浆液扩散半径随注浆压力和注浆时间的增加而呈非线性增大状态，前期增长速率较快，随后增长速率减缓；结合本工程施工参数分析，注浆时间取30 min，注浆压力从0.2 MPa增加到1.2 MPa时，浆液扩散半径从3.14 m增加到4.5 m；注浆压力取0.3 MPa，注浆时间从10 min增大到40 min时，浆液扩散半径从3.35 m增加到4 m；浆液的黏度时变性对壁后注浆扩散半径的影响较大，考虑浆液的黏度时变性，浆液扩散半径会减小，而且随着注浆压力和注浆时间的增大，浆液渗透半径减小的程度越大，特别是长注浆时间（40 min）情况下，浆液的扩散半径相对于不考虑黏度时变性时缩小34.9%，对注浆压力对围岩的支护效果及衬砌所受注浆压力的影响较大。

3.2 围岩应力

壁后注浆通过增加开挖土体的有效应力支护围岩，控制围岩的应力释放，防止开挖洞室的坍塌。结合本工程实例，考虑浆液的黏度时变性，设注浆时间为40 min，设置注浆压力P0为0.26，0.30，0.35及0.42 MPa共4种注浆方案，分别代入式（8），可以得到不同注浆压力条件下的浆液扩散半径r1，然后再将上述参数分别代入式（26）和式（27），得扩散区围岩的径向有效应力和切向有效应力随围岩距隧道中心距离的变化曲线，分别如图6和图7所示。

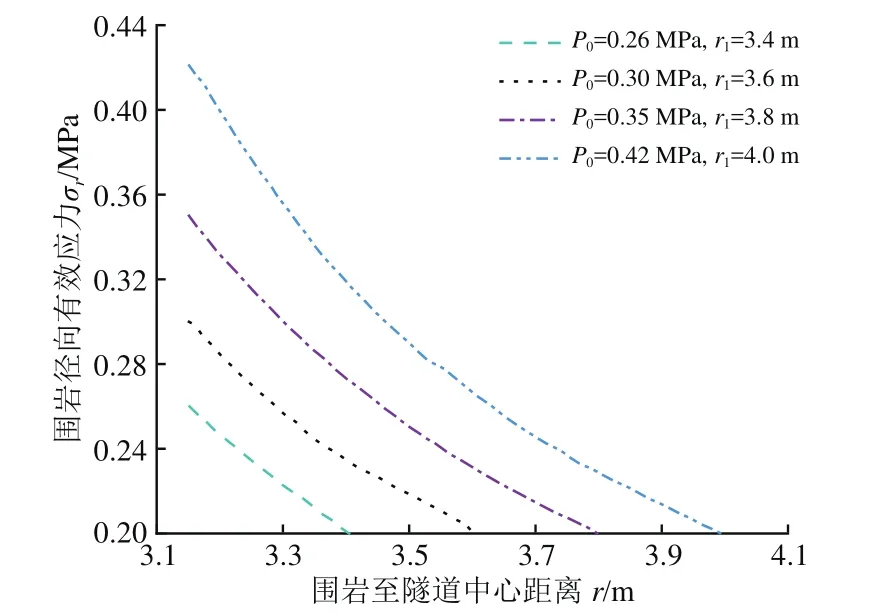
图6 围岩径向有效应力变化曲线

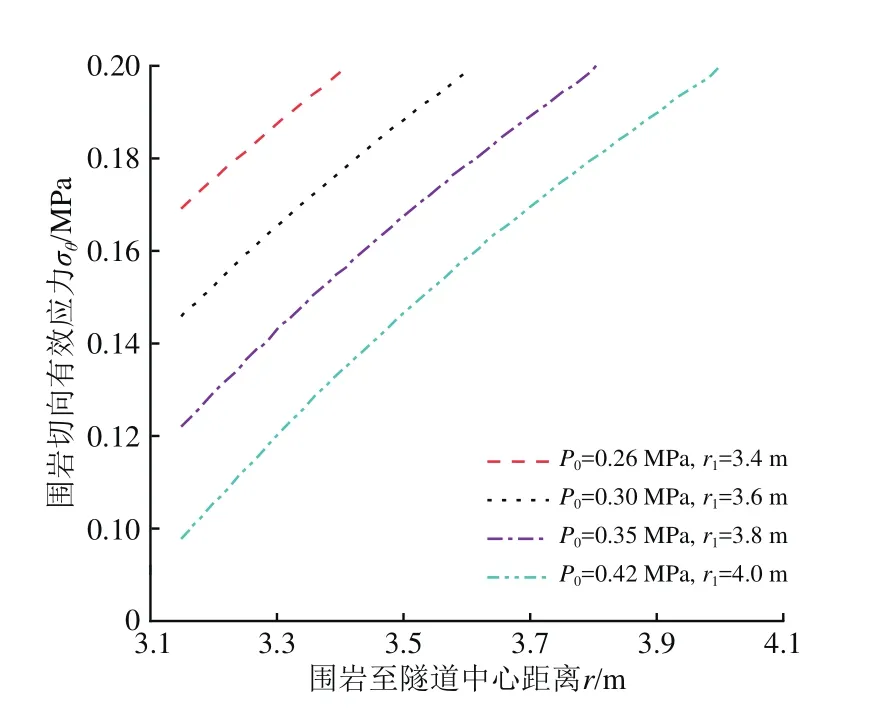
图7 围岩切向有效应力变化曲线

由图6和图7可以看出：4种注浆压力方案对应浆液扩散半径r1分别为3.4，3.6，3.8及4.0 m；壁后注浆可以增大扩散区内围岩的径向有效应力，减小切向有效应力，可以有效防止盾尾间隙处围岩临空面的坍塌，保证隧道的稳定性；扩散区围岩的径向有效应力随注浆压力的增大而增大，随着围岩距隧道中心距离的增大而减小，并且随着距离的增大其减小梯度逐渐减缓，在扩散边界处趋于原位围岩有效应力；扩散区围岩的切向有效应力随着壁后注浆压力的增大而减小，随着围岩距隧道中心距离的增大而增大，最终也趋于原位围岩有效应力。

3.3 围岩变形

结合本工程实例，考虑浆液的黏度时变性，采用与3.2节中同样的试验条件，根据式（28），代入具体施工参数可以得到围岩的径向位移随注浆压力和围岩距隧道中心距离的变化曲线，如图8所示。

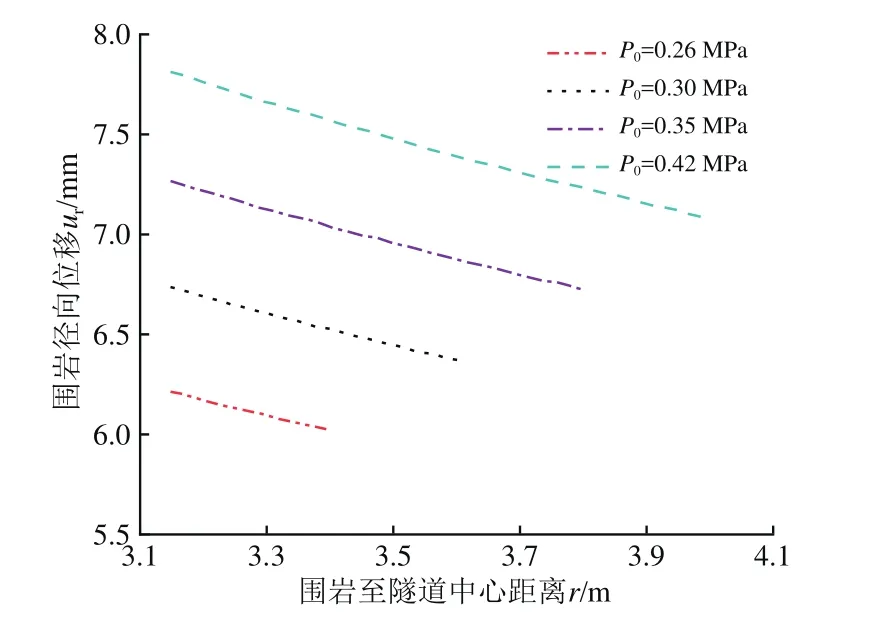
图8 围岩径向位移变化曲线

由图8可以看出：盾构隧道壁后注浆通过挤压围岩，控制围岩土体的变形；结合长沙地铁4号线施工参数，在高水压强风化砾岩中盾构隧道掘进，在注浆压力P0分别为0.26，0.30，0.35及0.42 MPa作用下，造成围岩开挖边界的位移ur分别为6.20，6.73，7.26及7.81 mm，增大了盾尾间隙的宽度，同时增加了保证注浆浆液填满盾尾间隙所需要的注浆量；扩散区围岩的径向位移随着注浆压力的增大而增大，随着围岩距隧道中心距离的增大而减小，基本呈线性变化。

综上，增大壁后注浆压力虽然可以一定程度上增大围岩的径向有效应力，防止围岩的坍塌，但过大的注浆压力势必会引起围岩产生较大的径向位移，增大盾尾间隙的宽度。实际施工要根据不同的地质条件选择合理的注浆压力，以保证隧道的安全。

4 结 论

（1）根据建立的渗透压力作用下围岩的径向有效应力、切向有效应力和径向位移的计算模型，结合实际工程实例分析可知，壁后注浆浆液扩散半径随注浆压力和注浆时间的增加而增加；当考虑浆液黏度时变性时，浆液扩散半径会减小，特别是长注浆时间（40 min）情况下，浆液的扩散半径相较于不考虑黏度时变性时缩小34.9%，施工时要充分考虑浆液黏度时变性对壁后注浆支护效果的影响。

（2）盾构壁后注浆浆液扩散时，扩散区围岩的径向有效应力随注浆压力的增大而增大，随围岩距隧道中心距离的增大而减小；切向有效应力的变化规律与径向有效应力的变化规律相反；二者在扩散边界处趋于原位围岩有效应力。

（3）盾构壁后注浆对围岩具有挤压作用，围岩的径向位移随着注浆压力的增大而增大，随着围岩距隧道中心距离的增大而减小。在注浆时间40 min、注浆压力0.42 MPa的工况下，围岩在开挖边界处的最大位移达7.81 mm。因此，实际施工中要根据不同的地质条件选择合理的注浆压力，以保证盾构隧道的安全。

（4）本文的研究成果是将城市地铁盾构隧道看作无限空间的平面轴对称问题推导得到的，而城市地铁盾构隧道埋深相对较浅，建议进一步研究时以半无限空间问题为理论基础进行分析探讨。