基于有限元法的铝合金门式抢修塔-线体系风振响应仿真研究

方子帆 孔 博 何孔德

(1.三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002;2.三峡大学 机械与动力学院，湖北 宜昌 443002)

架空输电线路易受到极端天气影响，从而造成断线、倒塔等灾害事件发生.基于南方气候条件和环境参数，且受传统拉线式门式抢修塔占地面积较大、场地环境受限等条件的影响，设计出一种能够在输电线路发生破坏，电力供给中断等情况下，继续满足电力需求的1C1W6-JZQL型门式抢修塔.该塔是根据广东省典型气象条件研发设计的单回路铝合金自立式抢修塔[1-5]，采用双地线，导线采用三角形排列方式及直线耐张通用设计的思路，其杆塔结构采用铝-钢组合设计，主柱模块化设计，施工简单，安装方便，安全性、可靠性、经济性好，对输电线路的抢修具有十分重大的意义.

依据《架空输电线路杆塔结构设计技术规定》、《架空输电线路设计》以及《铝合金结构设计规范》[6-8]设计出门式抢修塔的三维模型，利用ANSYS建立门式抢修塔、导线及“两塔一线”塔-线体系的有限元模型[9-10].通过Matlab软件模拟10级风场，运用AR自回归技术方法模拟脉动风荷载，分析门式抢修塔-线体系的力学性能、静力及风振响应特性，最后建立门式抢修塔-线体系失效判别公式，为铝合金门式抢修塔的设计奠定理论基础[6，11-15].

1 门式抢修塔-线系统有限元建模

1.1 使用环境

门式抢修塔的使用环境条件见表1.

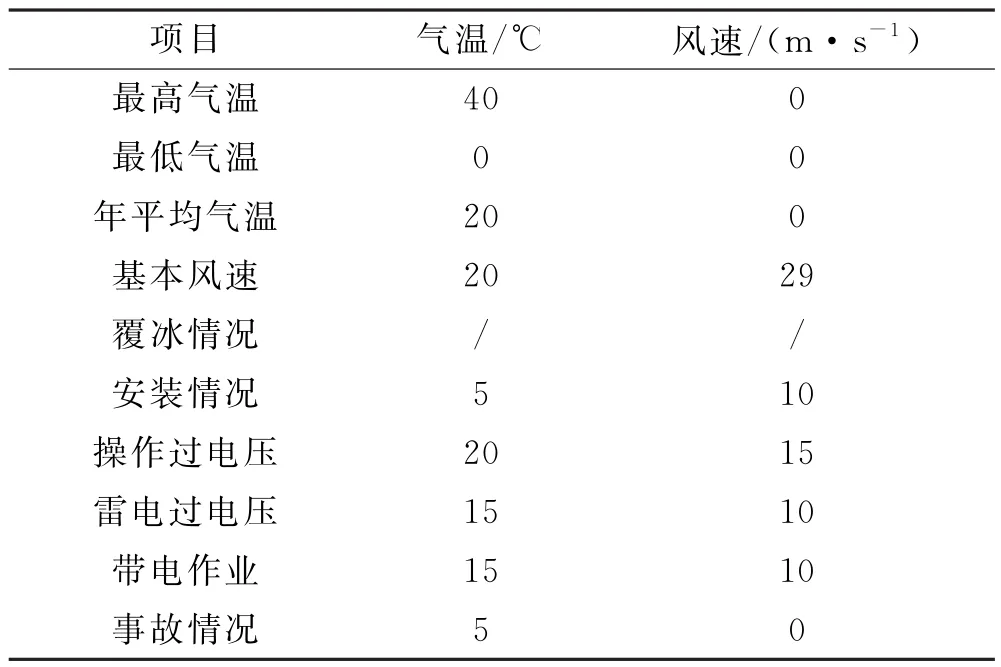
表1 环境条件

表中数据依据南方山地气象条件，参考《架空输电线路杆塔结构设计技术规定》及当地实际测量数据得出.

1.2 门式抢修塔结构及参数

抢修塔尺寸参数见表2.所用的铝合金牌号为2A12，其物理性能见表3.为了简化受力，对塔底部的16个节点施加固定约束，对两端导、地线与绝缘子连接处节点施加顺线路Z向位移约束，该模型符合门式抢修塔力学特性.

表2 门式抢修塔参数 (单位:m)

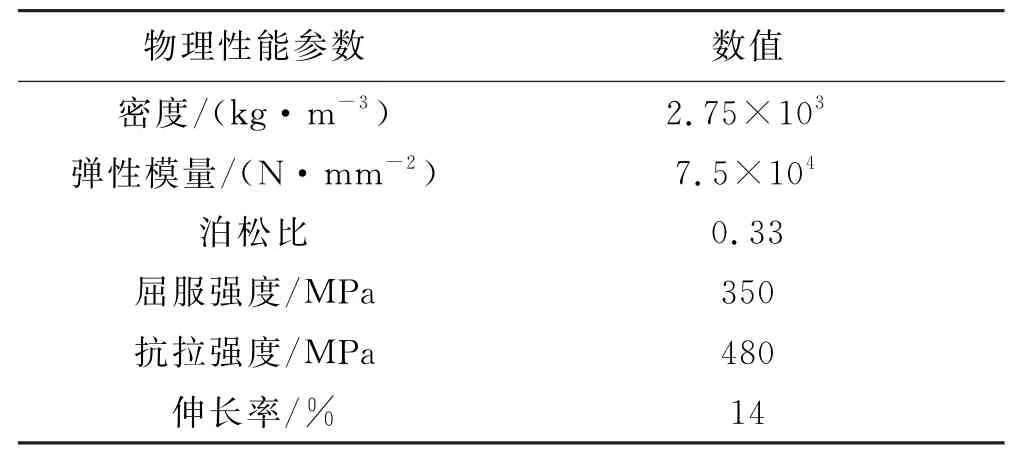
表3 2A12铝合金物理性能

为了便于运输组装且合理分类，抢修塔所使用的材料尽可能精简.将主要材料和辅助材料进行细化并分类，铝角钢构件型号见表4.

表4 门式抢修塔型材规格

1.3 有限元模型的建立

利用ANSYS建立抢修塔有限元模型.由于实际的抢修塔结构刚度很大，因此抢修塔整体结构采用梁单元模拟.梁单元各个端点包含X，Y，Z3个方向的位移和围绕三轴的扭转共6个自由度，并且门式抢修塔主材之间能传递竖向力、横向力以及弯矩，故选用BEAM 188单元来模拟其受力特性.门式抢修塔有限元模型如图1所示.

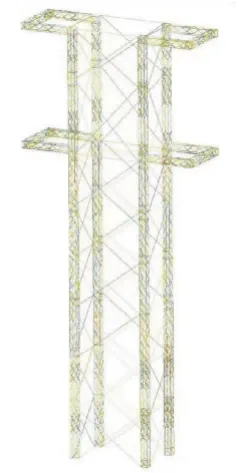
图1 门式抢修塔有限元模型

对导线建模时，首先要确定在重力作用下的初始位移.其次，为简化导线计算，将多根分裂导线等荷载转化为单根导线，等效后的力学性能与原多根分裂导线一致[5，12].本文选用悬垂线函数来确定导线几何形状，如图2所示，A、B两点为不等高的两悬挂点，AOB弧为架空导线形状，P为线上任意一点，O为导线的最低点，将A点定为坐标原点确立整体导线坐标系.

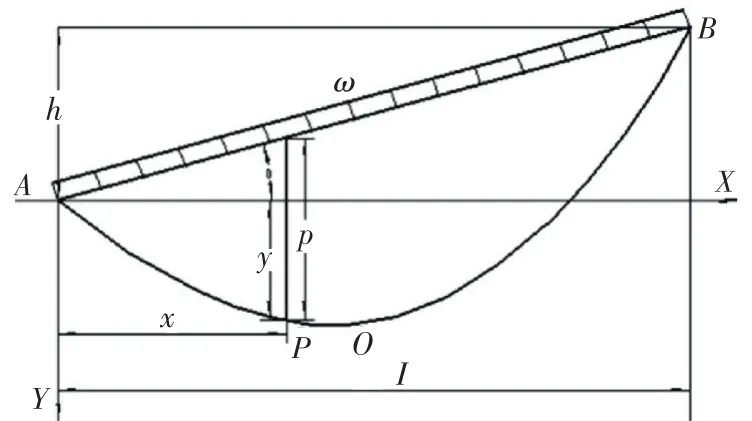
图2 悬链线几何形状示意图

假设导线自重力沿悬挂点A、B均匀分布，则悬垂函数式为:

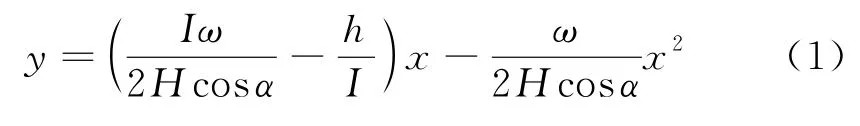
式中:x为低悬挂点的水平距离(m);y为低悬挂点的竖直高度(m);H为最低点的水平张力(N);α为导线两点连线与水平线的夹角.

门式抢修塔所受张力主要来自悬垂绝缘子串与导线、地线，大小与其选型及荷载计算参数相关.因此，根据不同导、地线的应用范围和强度条件，选择合适的导、地线，其基本参数见表5、6.

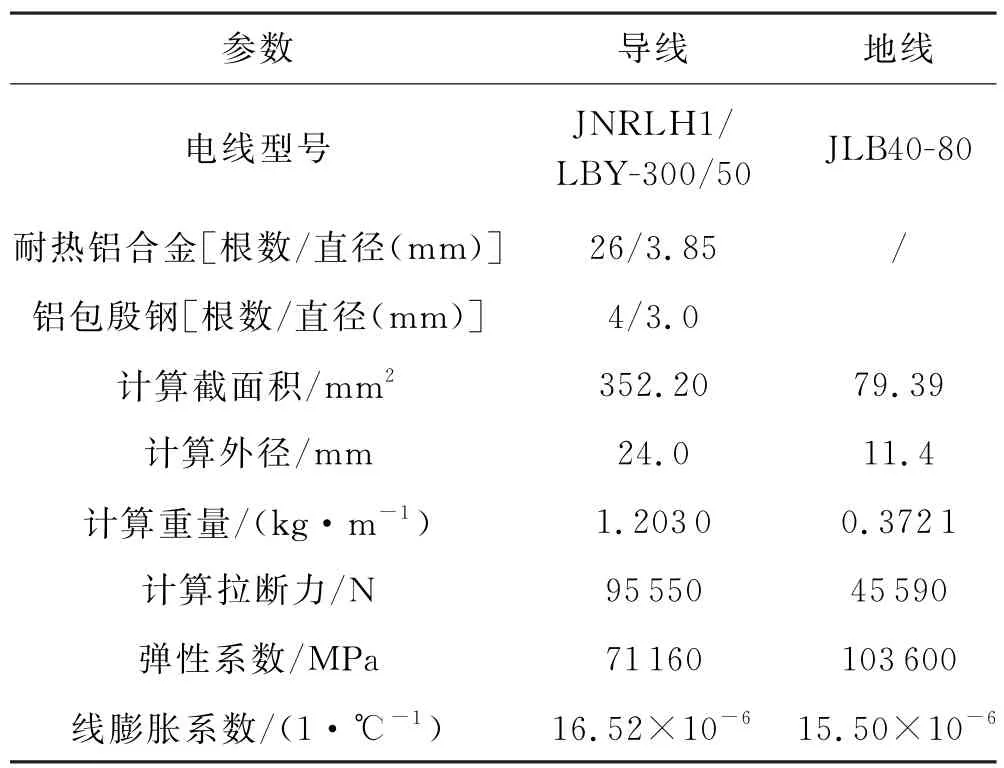
表5 导、地线型号参数

根据抢修塔单塔模型以及导线模型建立两塔一线有限元模型，如图3所示.

表6 绝缘子型号参数

图3 两塔一线模型

2 随机风场数值模拟

2.1 风载荷特性

对于一般高耸构筑物，平均风在一定的时间间隔内对构筑物作用力的大小、方向、作用点都不会发生改变.然而，脉动风是包含顺向、横向和垂向三维的湍流风，脉动风的周期比平均风短，一般在几秒左右.横向和垂向湍流风对高耸结构的影响并不明显，故本文仅考虑顺向脉动风场的影响.

自然风由平均风和脉动风两部分组成.空间中一点的风速表达式见式(2):

在分析结构风时，一般采用指数率平均风剖面，是Davenport通过大量实测数据提取风速的变化规律，并结合各类地形、地貌建立的风速沿着大气边界层内高度变化的计算公式.本文采用该指数率表达式表征各高度处的平均风速变化，表达式如下:

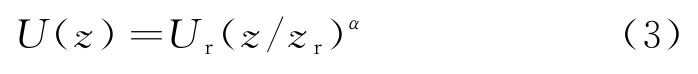
式中:U(z)取高度为10 m的基准风速;Ur为平均风速;z为任意一点;zr为平均风速处的高度;α表示地面粗糙度.

脉动风采用Davenport谱来模拟风速谱.Davenport提出了顺风向风速谱与离地高度无关，表达式见式(4):

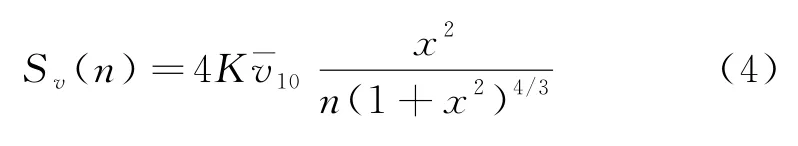
式中:K为表面阻力系数为考虑地面粗糙度后离地10 m高度处的平均风速;f为脉动风频率.

2.2 风场数值模拟

将门式抢修塔分为8段，模拟3个关键点处的风速谱.模拟点位置分别为塔底部跟开处、导线跨中最低点以及横担顶部.表7为风速模拟主要参数.

表7 脉动风速模拟主要参数

用Matlab仿真得到3个模拟点的脉动风速自功率谱和各模拟点的风速及风压谱密度.风速自功率谱如图4所示，水平顺风向风速时程如图5所示，水平顺风向风压时程如图6所示.

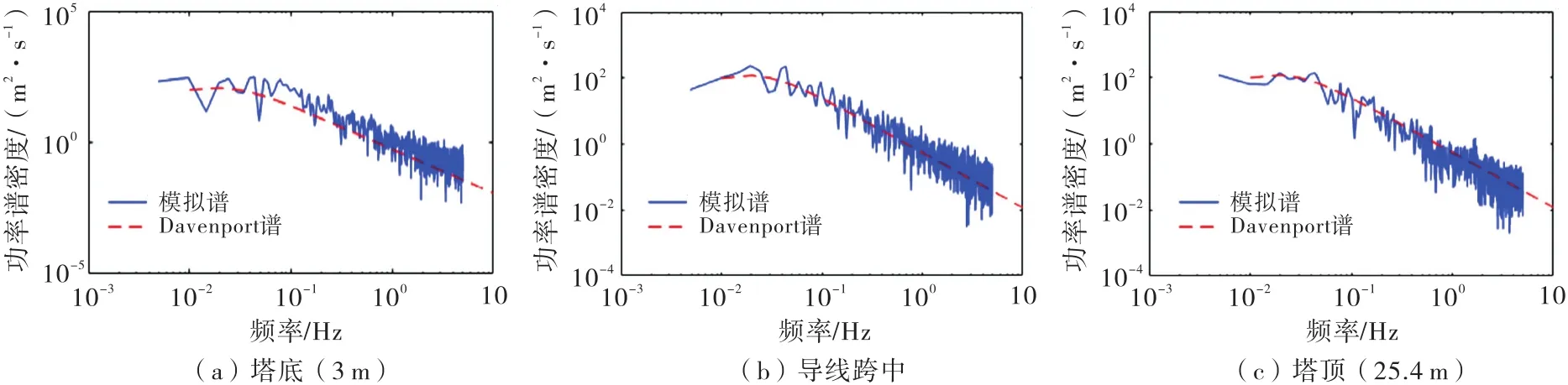
图4 塔-线体系自功率谱密度

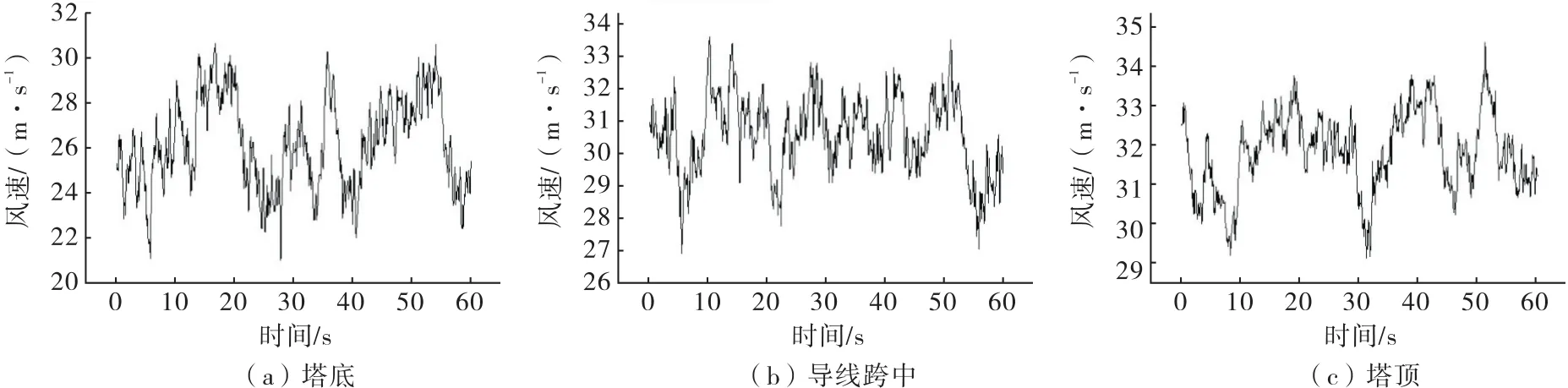
图5 塔-线体系脉动风速时程

图6 塔-线体系脉动风压时程

由图4可知，模拟谱与目标谱的总体均值接近且趋势一致，说明脉动风模拟的方法和效果有效可靠且精度较高，能用于塔-线体系的风振响应计算.

由图5可知，当基准风速为26 m/s时，塔底(3 m)处的脉动风速均值在26m/s波动;导线跨中处(18 m)的脉动风速均值在30 m/s波动;塔顶(25.5 m)处的脉动风速均值在32m/s波动.这是因为随着抢修塔纵向高程越高，风速大小逐渐增加.

由图6可知，塔底风压均值在0.85 kPa波动;导线跨中处风压均值在1.05 k Pa波动;塔顶风压均值在1.15 kPa波动.可见，风压也会随着高程升高而逐渐增加.

根据《110k V—750k V架空输电线路设计规范》可知，导线的水平风载荷计算公式为:

其中:Wx为垂直于导线及地线方向的水平风荷载标准值(k N);α为风压不均匀系数;W0为基准风压标准值(k N/m2);μz为风压高度变化系数;μsc为导、地线体型系数;βc为500 k V和750 k V线路导线和地线风荷载调整系数;d为导线或地线的外径;Lp为水平档距(m);B为覆冰时风荷载增大系数;θ为风向与导、地线之间的夹角;v为10 m处基准风速(m/s).

3 铝合金门式抢修塔-线体系风振时程响应

将模拟的脉动风压作用在塔-线体系中，得到动位移时程如图7所示.

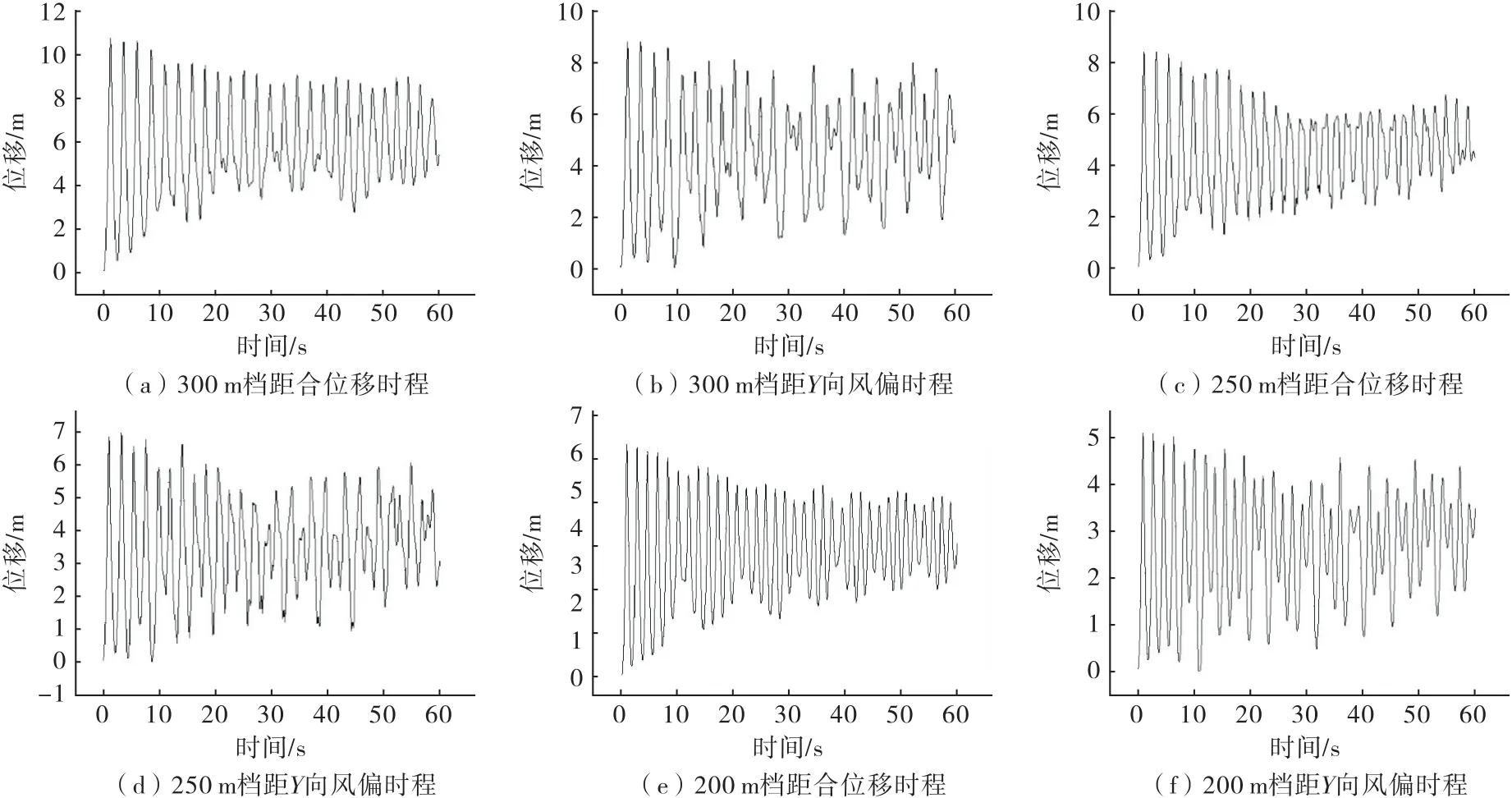
图7 塔-线体系动位移时程

由图7可以看出，仿真开始时在重力和风载作用下位移变化剧烈，在30 s后变形逐渐稳定.300 m档距导线合位移最大值为8741 mm，Y向风偏最大值为7630 mm;250 m档距合位移最大值为6725 mm，Y向风偏最大值为5 436 mm;200 m档距导线合位移最大值为5 027 mm，Y向风偏最大值为4 256 mm.由此可以看出，随着水平档距减小，导线合位移以及Y向风偏位移减小且振幅明显减小、振动频率降低.

塔-线体系动应力时程如图8所示.

图8 塔-线体系动应力时程

由图8可知，300 m档距塔-线体系动应力均值为140 MPa，250 m档距塔-线体系动应力均值为150 MPa，200 m档距塔-线体系动应力均值为140 MPa.因此，随着水平档距的增大，动应力均值变化不大，但幅值逐渐升高.

3种档距的导线张力时程如图9所示.

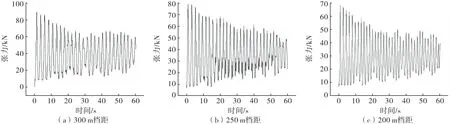
图9 塔-线体系动张力时程

由图9可以看出，300 m水平档距下的导线张力均值为67 808 N，250 m水平档距下的导线张力均值为61 872 N，200 m水平档距下的导线张力均值为50 450 N.

4 铝合金门式抢修塔-线结构准则评价

4.1 门式抢修塔构件的失效判别

分析大型复杂超静定结构体系时，当构件相继发生失效就会导致整体结构失效.当结构变形过大或者出现承载能力降低则认为结构体系失效.考虑抢修塔强度、刚度以及稳定性，根据失效准则判断抢修塔结构设计是否合理，采用以下4种失效判别准则:(1)结构多根杆件失效;(2)塔4根主材任意一根发生强度破坏;(3)塔结构中杆件失稳，整塔受力超过临界应力导致整个结构倒塌.

当达到3种状态中的任意一种即判定失效.在抢修结构体系中，拉杆为理想强度破坏，压杆多为稳定破坏.拉杆的承载能力计算表达式为:

式中:fy为材料的屈服强度;[σ]为许用应力;n为安全系数.门式抢修塔采用的2A12铝合金屈服强度可达350 MPa，根据《高耸结构设计规范》规定，安全系数取1.5～2.5之间，为计算简便取n为1.5.可计算门式抢修塔许用应力，见式(8):

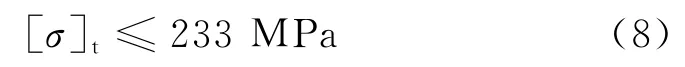
式中:[σ]t为拉杆许用内应力.

当拉杆内应力达到或超过许用应力时即认为拉杆失效.对于受压杆件，其破坏形式多为失稳破坏，在计算压杆抗压承载能力时，由许用应力乘以一个承载能力折减系数来计算得到.折减系数的取值主要与构件的长细比有关，可在0.3～0.5取值.为计算简便，将统一取为0.5，计算门式抢修塔许用压应力见式(9).类似地，当压杆内应力达到其抗压承载能力时即认为压杆失效.

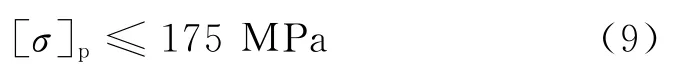
在风载和重力作用下，杆件所受应力主要为拉应力.根据风振响应仿真结果可知，3种档距下塔-线体系最大动应力为300 m档距下的240 MPa，已超过杆件抗拉承载能力限定值，需要在连接处设计加强结构或者更换强度更高的材料;250 m档距与200 m档距杆件所受内应力小于许用应力值.

根据材料的几何尺寸，同时参考杆件长度等，计算出构件长细比，见式(10):

式中:μ为长度因子;L为构件长度;i为构件截面对主轴回转半径.

根据所计算出来的长细比λ=49.5，结合材料的性能参数，计算出L型截面材料所能承受的临界应力，见式(11):

式中:σcr为临界应力;E为材料的弹性模量.计算得σcr=340 MPa，且抢修塔在风载作用下最大应力为240 MPa，因此门式抢修塔整体满足其保持原有平衡状态的能力，即不会发生失稳.

4.2 风载作用导线失效判定

导线最大的应力为导线的端部张力，由《架空输电线路杆塔结构设计技术规定》可知，在极端条件下，导线端部的最大张力不应超过综合拉断力的66%.表8为设计风速下的导线动张力与最大破断张力比较.

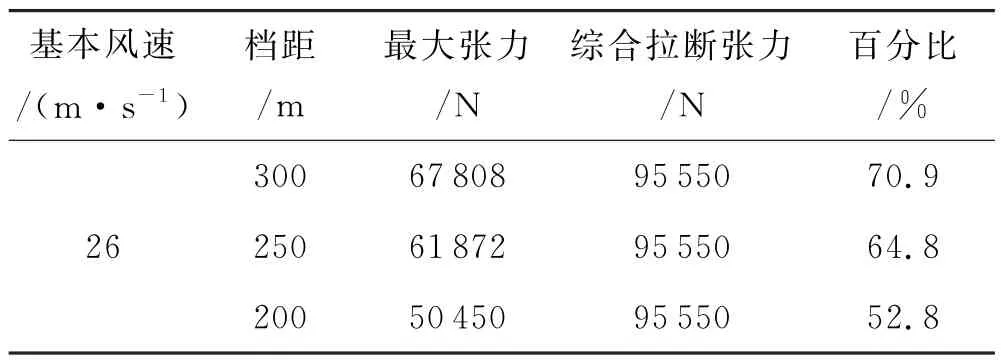
表8 导线动张力与最大破断张力

由表8可知，300 m档距最大张力占综合拉断张力的70.9%，大于技术规定中的66%;250 m和200 m档距下的最大张力占综合拉断张力分别为64.8%和52.8%，均在技术规定范围之内.因此，300 m档距不满足设计要求，250 m和200 m档距满足设计要求.

5 结 语

采用ANSYS有限元分析软件建立符合工程实际的“两塔一线”有限元模型(包括单塔模型、导线模型及塔-线体系模型)，对门式抢修塔单塔和塔-线体系两个模型进行了风振响应分析及抢修塔和导线的失效准则和破断依据判定.在风振响应分析中，研究了塔-线体系在3种不同档距下的风振响应特点，得到3种不同档距下的导线的动张力、塔-线体系的动位移及动应力，主要得到以下结论:

1)通过风振响应分析可知，由于导线长度增加导致整体的刚度变小，导线在迎风面上的位移显著增加，导线跨中最低点的位移从200 m档距的4 256 mm增长到300 m档距的7 630 mm.因此，在设计塔-线体系时，应适当降低两塔之间的水平档距来增大导线刚度，从而克服由于脉动风突变而发生倒塔的问题.

2)采用300 m档距需要在塔-线连接处设计增强结构或者更换强度更高的材料，若采用250 m或200 m档距设计门式抢修塔-线体系时，满足许用应力要求.

3)设计出一种输电线路发生破坏时的门式抢修塔-线体系，为后续研究提供了充足的理论依据.