基于模型的并网逆变器早期故障参数辨识

樊鹏帅 帕孜来·马合木提 魏胜风 刘 硕

(新疆大学 电气工程学院，乌鲁木齐 830046)

并网逆变器在实际运行中，由于受到外部工作环境及内部电热应力的影响，系统元器件的标称参数会发生退化现象.一般情况下，器件参数退化过程的特点是缓慢的、随机的，并伴有非线性和不确定性.当参数退化超出阈值即产生参数性故障.此类故障出现后通常不会使系统立即停机，但会使系统功能衰退陷入不确定状态，并诱发连锁效应:使系统输出特性逐渐改变，影响电能质量或逐步演变为严重的结构性故障，造成人员伤亡和财产损失.为了确保系统的安全平稳运行，需要在严重故障出现之前对故障源进行隔离.因此，针对系统开展早期故障诊断研究具有十分重要的现实意义.

近年来，非线性动态系统的故障诊断技术研究越来越受到重视.相关学者先后提出了大量的解决思路和方法[1].其中，基于模型的诊断方法(model based diagnosis，MBD)由于具有故障检测能力强和精度高等优点而受到广泛关注.具体实现机理在于需确定系统中各目标参数之间的映射关系，分析系统各故障模式所导致的工作参数变化，从而构建起系统模型.通过使用描述最贴近系统实际过程的数学模型，结合相关系统状态估计方法，把所研究对象的实际测量量与模型所表达的先验量加以对比而获得残差，通过对残差的分类处理进而实现故障源的诊断隔离.

牛刚等[2]对机车系统进行了BG建模，通过残差信号实现了对故障器件的诊断.彭小辉等[3]针对航天器推进系统的相关特性通过Z检验分析与GARRs相结合的方法，实现了对故障部件的诊断.文献[4]通过对NPC型逆变器进行BG建模并设计了自适应阈值，减少了误报警，完成早期故障源的定位.上述文献均是在建立诊断对象的BG模型后，推导出系统的GARRs，然后获得故障特征矩阵(fault signature matrix，FSM)，最后将系统的实际观测特征向量与FSM对比，得出诊断结论.然而上述方法只能检测到故障的发生，定位到退化故障部件，并不能对部件的退化程度做出判别.从故障诊断与隔离(fault diagnosis and isolation，FDI)的角度出发，当检测系统追踪到故障源时就需要获得元件的损伤度.所以一旦发现故障源，能估计故障器件的参数值就比较重要.

参数辨识是通过相关算法来估计所研究系统中的不确定性参数，应用于FDI时主要是分析系统的退化参数，评估当前系统的健康状态.从FDI角度出发，参数辨识研究从一定程度来讲既是对故障检测的验证也是对它的定量分析.因此，针对已发生退化行为的系统开展参数辨识研究对系统的早期故障诊断及寿命预测都具有重要意义.文献[5-6]通过混合逻辑动态建模，分别建立了电力电子电路开关器件导通与关断条件下的状态方程，并将不同模态下的电路方程整理得到电路混杂模型，实现了DC/DC电路的参数辨识.然而，对于具有多个开关管的复杂电路，系统有较多模态相互耦合，使得该建模方法变得十分繁琐且困难，难以实现系统内目标参数间作用机理的描述.

因此，本文以三电平T型逆变器主电路为研究对象，基于BG理论建立系统的HBG模型，通过观测信号和系统行为约束关系推导出了能够反映系统内部各系统参数之间相互作用关系的GARRs，并由GARRs构造出目标函数，进而将系统参数的辨识问题转化为对函数的优化问题，最后通过SSA算法对目标函数进行参数寻优，完成参数辨识.

1 相关背景

1.1 T型逆变器简介

T型逆变器目前已经广泛应用于光伏逆变等领域，主电路拓扑结构如图1所示，开关状态及输出电压见表1.

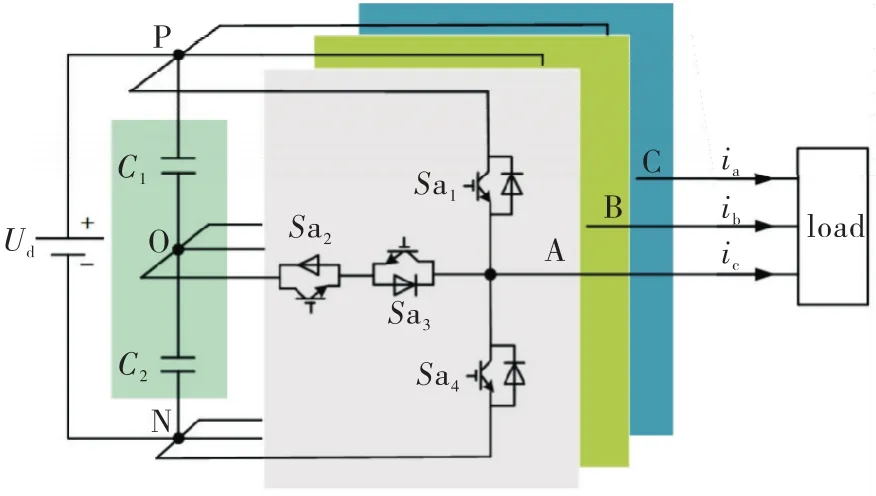
图1 T型逆变器拓扑结构图

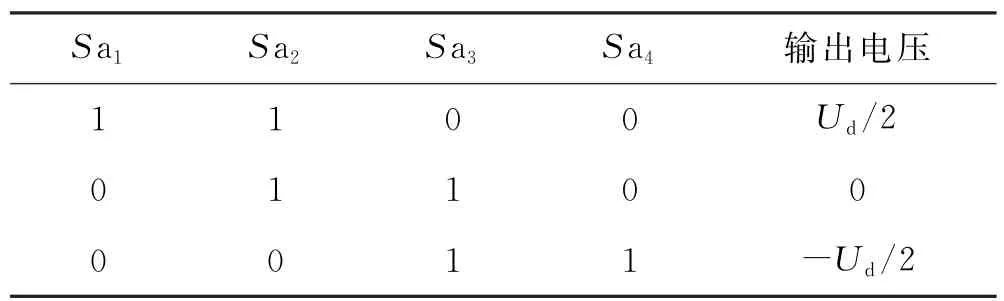
表1 开关状态及其输出电压表

1.2 键合图理论

键合图全称为功率键合图，是物理系统的图形化表示.BG理论按照一定规则采用键合图符号语言{Se，Sf，R，C，I，TF，GY，1-，0-，De，Df}等键合图元、键、通口来描述所研究对象.

在BG建模时，实际物理系统以功率键为能量媒介，由通口实现子系统间的能量传递.系统通过势源Se、流源Sf、耗能元件R、储能元件C(容性)和I(惯性)、变换器TF、回旋器GY、共流结1-结、共势结0-结等BG元件按相应规则构建成BG模型[7].应用于电气系统时，电变量与BG广义变量的对应关系见表2.

表2 电变量与BG广义变量对应关系

1.3 系统退化特征

相较于结构性故障，参数性故障发生后，系统输出在一段时间内并不产生较为明显的变化，然而系统本身却陷入退化状态.相关研究表明，功率开关是系统中最为脆弱的元件，引起功率器件IGBT性能退化失效的原因主要分为两大类:物理层失效和电气失效.浙江大学刘丹等[8]通过实验研究，提出将IGBT导通电阻Ron作为器件退化指标.文献[9-10]指出Ron是监测功率开关器件健康状态的预兆参数，并定义导通电阻值增加了初始值的25%作为其失效判定标准.文献[5]指出，同等的温度条件下，当电解电容的容值C减小20%或者等效串联电阻RC增加为初始值的2～3倍时，该电容可视为失效.

2 基于BG理论的数学模型建立

2.1 键合图模型搭建

由于功率开关器件IGBT的存在，逆变器系统正常工作情况下在各工作模态间相互切换，导致系统离散事件和连续事件相互耦合，呈现出强非线性特征，属于典型的混合系统.目前，逆变器的数学模型多基于基尔霍夫定律列写状态方程获得，状态变量选取与储能元件有关，且较少涉及包含主电路中非理想器件的系统运行机制的建模.以BG方式建模的优势在于能够从能量角度出发建立起系统的元件级模型，从而对逆变器这类混杂电路内部器件间的相互作用关系进行充分且完备的描述.本文考虑的非理想功率器件IGBT以导通电阻Ron为退化特征参数，建模过程中以键合图1通口阻性元件R表示.

根据键合图理论中的节点法[11]建模方法，所建立的三电平T型逆变器HBG模型如图2所示.为方便起见，每相输出负载以R-L代替，如果考虑滤波装置或者其他后延系统可继续在每相输出结点后进行BG建模.其中，直流侧以势源Se作为系统输入，Rc1、Rc2分别为钳位电容C1、C2的等效串联电阻，11～14为开关结点，α取值为布尔变量{0，1}，与控制信号SPWM有关.在键合图工具20-sim中将阻性元件Ron与可调制变换器MTF相连以接收控制信号[12].Ca1、Ca2、Cg1是为消除代数环而存在，取值为一个极小的常数，对系统并不构成影响.

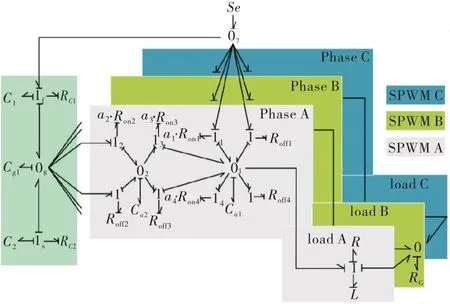
图2 T型逆变器HBG模型

2.2 系统解析冗余关系

由HBG模型推导的GARRs以一种紧凑有效的方式描述了混合系统所有运行模式下的行为特征，由遍历路径法推导并消去未知变量而获得的系统行为约束关系，包含了系统的控制信号、输入信号、外部检测量及系统本身结构参数等.在任何条件下，系统都满足该行为约束关系.GARRs可以由式(1)表示为:

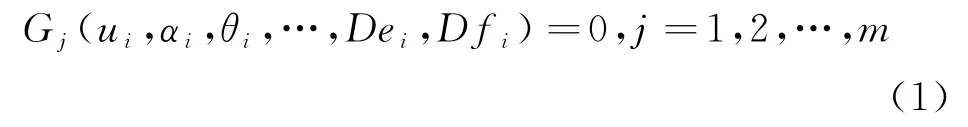
其中:ui为系统输入参数;αi为控制量参数;θi为系统参数;Dei为势传感器采集量;Dfi为流传感器采集量;i为参数个数;m为GARRs数量.

针对本文研究对象，均以A相为例进行说明.GARRs的推导过程可描述为:选定01、02、07、08、1f、1s这几个结点来推导GARRs，先对所有功率键和各个结点进行标号，在结点01、02、07、08处分别加入势传感器De1、De2、De7、De8，在结点1f、1s(普通1-型结点)分别加入流传感器Df1、Df2.T型逆变器A相的诊断键合图如图3所示.

图3 A相诊断键合图

以01结点为例，存在式(2)的解析冗余关系:

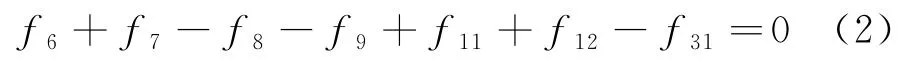
式中:

由式(2)和(3)得到01节点的GARRs为式(4):

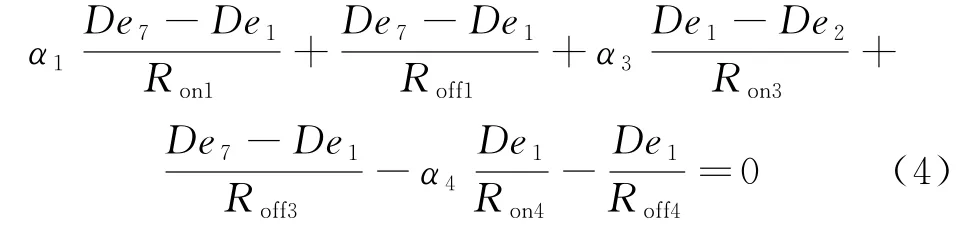
类似地，结点02、07、08、1f、1s的解析冗余关系式可以分别获得.同理，在B相、C相相同位置放置De可进一步得到整个系统的GARRs.T型三电平逆变器的BG模型参数表见表3.

表3 T-BG模型参数表

2.3 目标函数构造

函数构造的机理在于:以系统待辨识的参数作为目标参数，考虑到实际情况，如果目标参数是系统中的真值，则通式(1)的值应为0或在近乎为0的小范围内波动.则令Gj中θi={θia，θib}，并以θia作为目标参数，表示从故障参数隔离模块中选择的故障参数集合，而θib代表已知的元素且不包含于集合θia的系统参数集合.构造出目标函数作为适应度函数，见式(5).由此将故障参数辨识问题转化为对目标函数的优化问题.

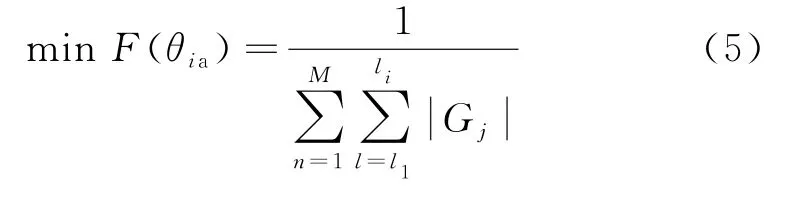
其中:M为监测信号有效采样点数;li表示系统行为约束方程个数.将待辨识参数及采样数据带入目标函数，以θia作为目标参数通过极小化目标函数来寻求最优解，从而获得故障参数θia.

采用GARRs估计目标参数时，只选择包含目标参数的GARRs.这里，利用GARRs的优点特性可以建立M个采样间隔的成本函数，这样就能使用M个数据的集合来实现故障参数的故障估计，即使该系统在M个采样间隔中历经了运行模式的变化[13].

3 基于SSA的故障参数辨识

3.1 辨识模型

由1.3节，并网逆变器经过长时间服役后，内部相应元器件的参数退化将加重，而关键器件IGBT表现为导通电阻的增大.因此，本文以元件IGBT退化故障为故障因子进行基于SSA和BG模型的参数估计.系统BG模型如图2所示，以A相为例，选择关键器件以{Ron1，Ron2，Ron3，Ron4}作为故障源.整个辨识流程如图4所示.

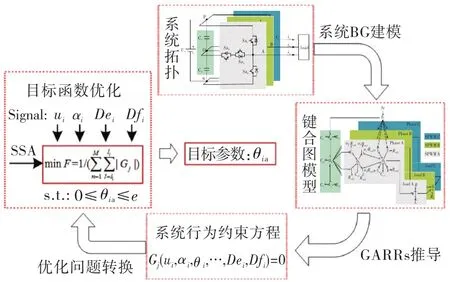
图4 辨识流程图

针对本文研究对象，可建立以下目标函数:

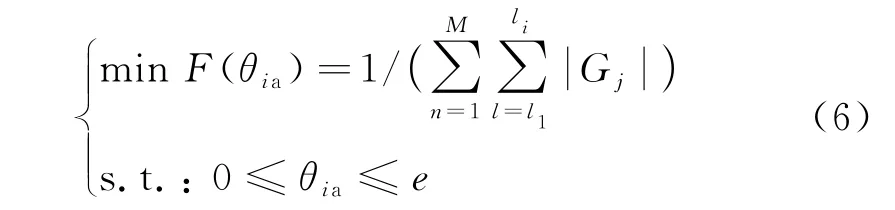
选择目标参数θia={Ron1，Ron2，Ron3，Ron4}，优化问题一般需要设置参数寻优范围和约束条件，而θia在退化过程中是增大的，则可设定搜索范围为:0≤θia≤e，其中e为元器件失效判定阈值.

3.2 麻雀搜索算法

SSA算法是在2020年由东华大学薛建凯提出的一种新型群智能优化算法[14].SSA模拟麻雀捕食过程进行迭代寻优，与其它智能算法相比，具有搜索能力强、稳定性好、收敛速度快、调节参数少等优点.由n只麻雀组成的解空间和适应度值空间可表示为式(7)形式.

式中:X代表种群集合;d代表优化问题变量维数;n为个体数量;F(x)为麻雀适应度值.

执行SSA时，发现者可视为种群的向导，其本身拥有较大的搜索空间，数量一般占据整个种群的10%～20%.而具有较好适应度值的向导可享有觅食空间内的优先权，并对整个种群包括加入者的觅食方向负责.

在每次迭代时，发现者位置按式(8)更新，加入者位置按式(9)更新，侦察者位置按式(10)更新.

式中:Xij表示第i只个体在第j维的位置，j取值范围为[1，d];t代表当前迭代数;s为(0，1]的随机数;rmax表示最大迭代次数;Q是服从正态分布的随机数;L表示一个内部元素都为1的1×d的矩阵;la表示警戒值，取值范围[0，1];Ts表示安全阈值，取值范围[0.5，1].当la＜Ts时，表示觅食环境安全，发现者可以执行搜索行为;当la≥Ts时，表示发现者种群发出报警，需要撤离.

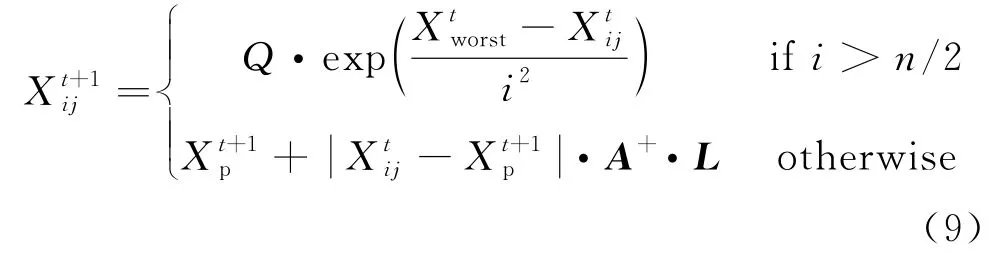
式中:n为种群规模;Xp是当前向导所占据的最优位置;Xworst是当前全局最差位置;A为内部元素随机赋值为1或-1的1×d矩阵，并且满足A+=AT·(AAT)-1.当i＞n/2时，适应度值较低的第i个加入者去别处觅食.

式中:Xbest为当前全局最优位置;步长控制参数β是服从均值为0、方差为1的正态分布的随机数;K表示麻雀个体移动方向和步长控制参数，是取值为[-1，1]中的随机数;fi为当前个体适应度值;fg、fw分别是当前全局最佳和最差适应度值;ε为最小常量，防止分母为零.

3.3 SSA辨识流程

基于麻雀搜索算法的早期故障参数辨识流程图如图5所示.

图5 SSA寻优流程图

SSA-BG模型参数辨识过程步骤如下:

1)设定参数维度、迭代次数、种群规模、发现者数量、安全阈值;

2)在搜索空间内随机初始化种群并计算适应度值，保留当前最优个体;

3)按照式(8)～(10)更新相应位置，比较适应度值并存储每一代最优值;

4)更新整个种群所经历的最优位置和适应度值.

4 实验分析验证

4.1 实验介绍

实验以20-sim和Matlab软件工具为实验平台，在20-sim平台搭建逆变器系统HBG模型，通过在图3的标定位置分别放置势传感器、流传感器，并将采集的开关信号导出数据至Matlab工作区，由SSA对目标函数进行寻优处理.

以T型逆变器A相为例进行说明，分别设定故障参数即为目标参数:θia={Ron1，Ron2，Ron3，Ron4}.实验将目标参数设定为1.00，开关频率为20 k Hz，采样频率为100 k Hz，麻雀种群规模为800，最大迭代次数为300，安全阈值为0.8，发现者比例为0.2.

只要辨识算法能够在终止条件之前使目标函数收敛并找到对应的目标参数θia，通过误差分析能满足可接受条件即为辨识成功.

4.2 辨识结果及分析

实验采集5 680组数据，共做10组实验，根据图5所示流程进行实验验证.由SSA优化目标函数所得适应度曲线结果如图6所示，终止代数为300.

图6 目标函数适应度曲线图

通过SSA对模型参数进行辨识后取均值以避免单次辨识结果出现较大误差的情况，得出系统退化参数辨识结果，见表4.

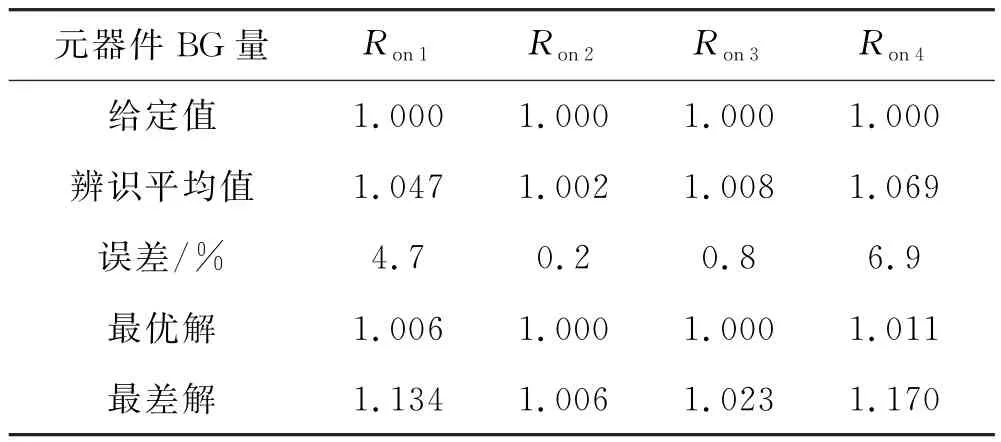
表4 目标参数辨识结果

由表4可见，辨识结果误差最大值不超过6.9%，最小误差为0.2%.表明了基于BG理论结合SSA辨识故障参数的有效性.

5 结 论

本文以电气系统中的混杂电路:三电平T型并网逆变器为研究对象，将系统IGBT参数退化视为故障因子，建立了系统HBG模型，推导出了系统的GARRs，并将系统故障参数的辨识问题转化为对目标函数的优化问题，采用SSA寻优算法完成了系统退化参数的辨识.通过联合仿真实验验证了该方法的有效性和可行性，为混杂电路的参数辨识提供了思路，即基于BG理论对系统进行HBG建模，推导GARRs并结合相关算法对故障参数进行辨识分析，以获取系统当前的退化状态，为系统的视情维护提供依据.