放坡开挖下深基坑开挖坡体稳定性研究

王 飞

（安徽省皖江城际六庆铁路股份有限公司，安徽 合肥 230000）

1 引言

边坡稳定性分析是边坡工程的核心问题，目前应用于边坡稳定分析的方法主要有基于极限平衡的传统方法和基于强度折减技术的有限元法[1～4]。极限平衡法通常根据岩土体潜在可能的破坏面上土体外力与内部抗力之间的平衡，来求解边坡的抗滑稳定安全系数，但该方法为了便于计算的进行作出许多假定[5～6]，也无法分析土体破坏的产生和发展过程。随着有限元计算的发展，20世纪70年代有限元法逐渐被引入到边坡稳定分析中[7],且得到较广泛的应用。该方法克服了极限平衡法的不足，不但满足力的平衡条件，而且充分考虑了材料的应力—应变关系及支挡结构与土体的相互作用，计算过程中也无需作任何假设，使得计算结果与实际更加吻合。基于有限元法的上述优点,近年来其在基坑、边坡等各种岩土工程稳定性分析中得以广泛应用。Griffiths等[8]论述了如何将理想弹塑性有限单元法与强度折减技术相结合分析二维边坡的稳定性；郑颖人等[9～10]在强度折减法基本理论和提高计算精度方面进行了系统性的研究；陈寅春等[11]采用有限元强度折减法研究了多级边坡的几何参数对边坡稳定性的影响，赵尚毅等[6]将有限元法运用到边坡稳定性计算中，通过对计算结果的分析表明有限元法的可靠性。

目前对于边坡稳定性的研究虽然已相对成熟，但对放坡开挖下深基坑开挖坡体稳定性研究缺乏系统性研究，作者结合工程实例采用有限元强度折减法分析坡脚处基坑开挖过程中多级边坡的级数、坡率、平台宽度及岩土体内摩擦角和黏结力对边坡稳定性的影响，希望对今后类似工程的分析具有一定的指导作用。

2 有限元强度折减法

2.1 基本原理

有限元强度折减法最初是由Zienkiewicz等人[7]提出。其原理就是假设土体的弹性模量E和泊松比v保持不变，将粘聚力c和内摩擦角φ同时除以一个折减系数F，得到一组新的c′和φ′，表达式为：

将得到的一组新的c′和φ′作为土体参数重新输入，进行有限元试算直到计算发散为止，此时的F即为土体稳定系数。

2.2 屈服准则的选取

假定σ和τ分别表示土体内某剪切面上一点的正应力和剪应力，该点在极限状态下，剪切破坏面上的σ和τ的关系可表示为：

主应力可表示为：

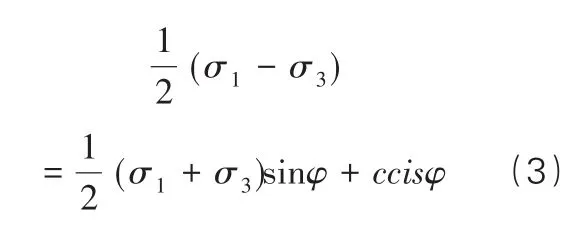
土体采用Mohr-Coulomb准则的弹塑性本构模型，其表达式可表示

其中I1为应力张量的第一不变量，J2为应力偏量的第二不变量，θ为应力罗德角。

3 边坡稳定因子敏感性分析

某隧道基坑长约132m，施工方法为明挖顺作法，基坑开挖采用大放坡加悬臂直立开挖的形式（图1）。为了全面分析多级边坡稳定性的影响因子对其稳定性的影响并优化设计，以该工程为背景设计不同比较算例，采用单因子变量法对比分析多级边坡的级数、坡率、平台宽度、岩土体内摩擦角和黏结力等对边坡稳定性的影响。岩土材料参数采用加权平均值:泊松比μ=0.3，内摩擦角φ=40°，弹性模量E=150MPa，重度γ=24kN/m3，黏聚力c=18KPa。在实际边坡有限元模型中，按照非常典型的边界约束类型施加边界约束。

图1 基坑几何模型（单位：m）

3.1 边坡级数对边坡安全系数的影响

本文设计了15组比较算例以研究放坡开挖下深基坑不同开挖深度时，边坡级数对边坡安全系数的影响。其中，基坑开挖深度由1m增加至5m，边坡级数分别取1、2、3级（图2）。采用有限元强度折减法进行计算，计算结果如图3所示。

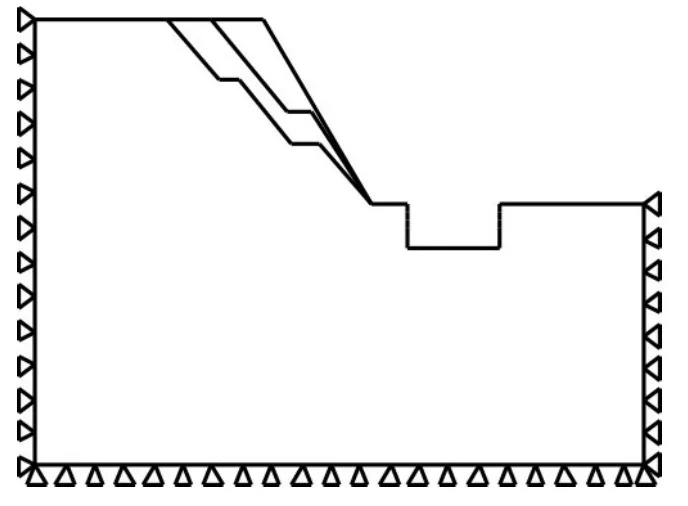
图2 计算模型

图3 稳定性系数与开挖深度的关系

由图3可见，随着开挖深度h的增大，边坡安全系数F缓慢减小，最后趋于一定值；且h相同时放坡级数越多，边坡安全系数F越大，其稳定性越好，这与陈寅春[11]的研究规律一致。提取h=5m情况下不同级数边坡临界失稳状态的最大剪应变云图（图4）。对比可知不同边坡级数下最大剪应变区域随着边坡级数的增多而不断增大。

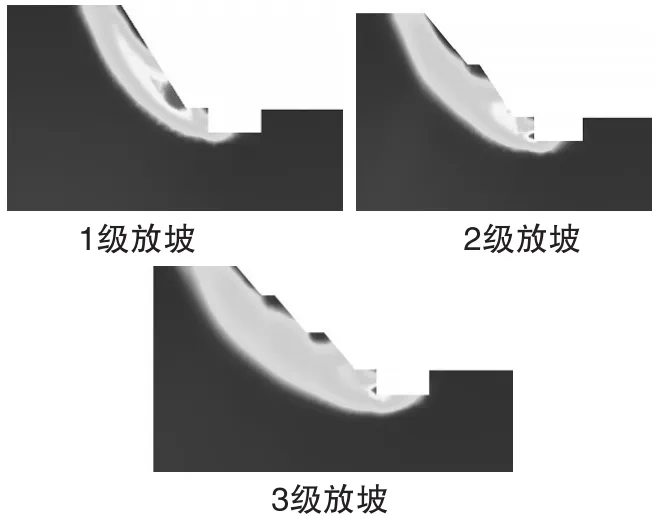
图4 最大剪应变云图

3.2 边坡坡率对边坡安全系数的影响

边坡坡率是边坡稳定性的重要影响因素之一，随着坡率的增加，边坡的稳定性将降低。对于3级边坡具有多种坡率（如图5，分别用a、b、c表示），每一级坡率的改变对边坡稳定性的影响均不相同。建立有限元模型，分别计算得到坡脚基坑不同开挖深度下多级边坡稳定性系数（图6）。

图5 计算模型

图6 稳定性系数与开挖深度的关系

由上述分析可知，放坡高度保持不变，边坡安全系数随着任意一级边坡坡率的增大而减小，且不同级的坡率的改变对于边坡安全系数的影响程度均不相同。由图6可见，随着放坡坡脚处深基坑开挖深度的不断增加，边坡安全系数不断减小，对于多级边坡来说，下部坡率变化对安全系数的影响比上部大。

图7为h=5m时不同坡率下放坡开挖坡体临界失稳状态的最大剪应变云图。由图可见随着坡率的增大边坡临界失稳时，最大剪应变区随之减小，且位于下部的坡率变化时对最大剪应变区影响更加明显。

图7 边坡最大剪应变云图

3.3 平台宽度对边坡安全系数的影响

在不改变多级边坡高度及坡率的情况下，建立不同的计算模型以探讨平台宽度的尺寸效应。如图8所示，对于多级边坡每级平台宽度用d、e表示，平台宽度对边坡安全系数的影响见图9。

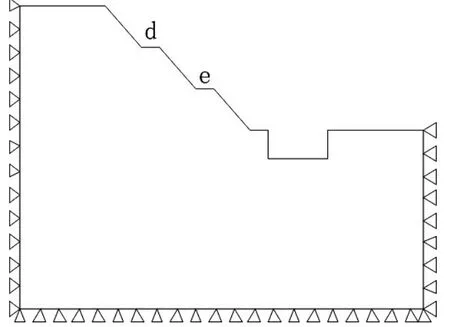
图8 计算模型

图9 稳定性系数与开挖深度的关系

分析可知：放坡高度一定时，平台宽度的减小导致边坡安全系数降低，且减小相同的边坡宽度，下部平台的变化对安全系数的影响比上部大。边坡稳定系数F随着开挖深度h的增大而明显减小，当d=e=4m时，安全系数由h=0m时的2.23减小至h=5m时的 1.75 减小幅度约27.4%。提取h=5m时多级边坡临界失稳状态的最大剪应变云图(图10)，由图可看出，随着平台宽度的减小，边坡临界失稳状态的最大剪应变区域不断减小。

图10 边坡最大剪应变云图

3.4 内摩擦角对边坡安全系数的影响

基坑开挖深度由1m增加至5m，摩擦角变化范围为30°～50°。算例中取坡率a=b=c=1:1,平台宽度d=e=4m，黏结力c=18kPa，计算得到摩擦角φ对于边坡稳定性的影响如图11所示。

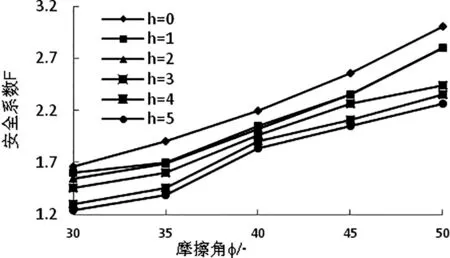
图11 内摩擦角对边坡安全系数的影响

由图11可知，随着内摩擦角的增加,安全系数明显增大,说明边坡稳定性对于内摩擦角的变化十分敏感。当坡脚基坑开挖深度h在2m～4m时，不同关系曲线相互之间已接近重合，说明此时基坑的开挖深度对于边坡稳定性影响较小，但当开挖深度h＞4m时，必须采取相应的加固措施，这对其他类似边坡的设计和施工提供良好的参考价值。提取h=5m时边坡临界失稳状态的最大剪应变云图（图12），由图12可看出，随内摩擦角的增加，剪应变变形带分布的形状基本不变均呈圆弧状，但土体剪应变区域由基坑底面逐渐转向基坑拐角处。

图12 边坡最大剪应变云图

3.5 黏聚力对边坡安全系数的影响

黏聚力作为土体重要的物理力学指标，探究其对边坡土体稳定性的影响很有必要。采用单因素变量法探讨不同开挖深度下粘聚力c(c变化范围为18kPa～40kPa)的改变对于边坡稳定性的影响。安全系数F与黏聚力c的关系曲线如图13所示。

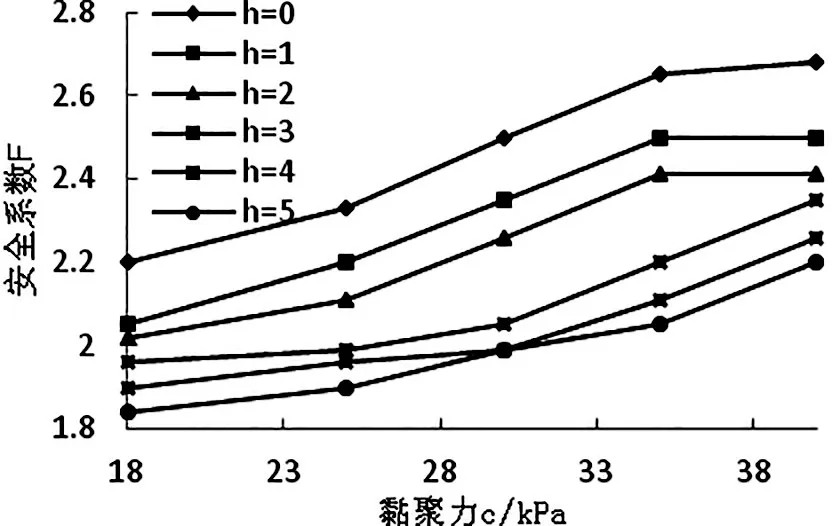
图13 黏聚力对边坡安全系数的影响

从图13可看出，随着粘聚力的增大，边坡安全系数逐渐增大,且不同曲线呈现的规律基本一致，说明粘聚力是影响边坡稳定性的重要因素之一。从图13中也可以看出,当黏聚力从18kPa增加到35kPa时，对于h=0m情况下，安全系数增加了约0.5，但对于h=5m其增加约0.2，说明开挖深度较浅时粘聚力对安全系数影响较大,但随着h的逐渐增大,其作用不断降低。由h=5m时边坡临界失稳状态的最大剪应变云图（图14）可看出，随着黏结力c的增大，土颗粒之间的吸引力不断增大，临界破坏状态下会有更多土体参与抵抗边坡滑动，抗滑力随之提高，边坡稳定系数不断增大。

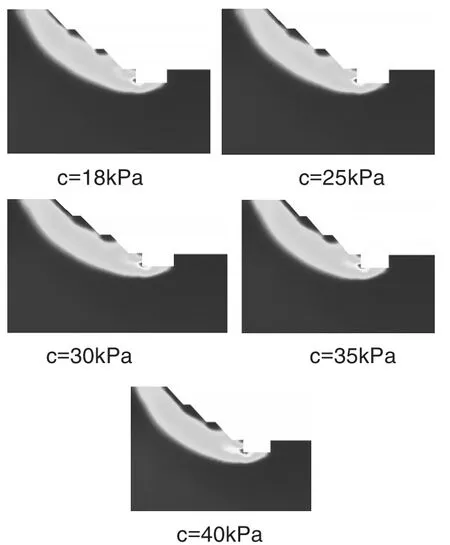
图14 边坡最大剪应变云图

4 结语

本文结合工程实例运用有限元强度折减法分析了边坡的级数、坡率、平台宽度、内摩擦角及黏结力对边坡安全系数的影响，通过计算分析优化了设计方案并获得如下结论：

①对于高度一定的多级边坡，坡脚处的基坑开挖会导致边坡稳定性降低，且随着开挖深度逐步加大，其稳定性逐步降低；

②在坡高一定的情况下，边坡级数越少、坡率越大、平台宽度越小，其临界失稳状态的最大剪应变区域不断减小，导致安全系数越低；

③内摩擦角和黏聚力对边坡稳定性的影响较为敏感，对于实际工程可考虑通过提高土体内摩擦角和黏聚力（如注浆加固）的措施来提高边坡稳定性。