追寻有效策略,让练习讲解充满灵动

裘兴亚

摘要：数学习题是数学课程的一个重要组成部分，在合理、灵活运用习题基础上，采用适当的讲解方法，能提高数学课堂效率，增强教学有效性。本文试从五个方面谈谈如何讲解习题，有效引导和促进学生自主学习，发展学生思维能力。

关键词：习题;讲解;有效;引导。

数学习题是数学课程的一个重要组成部分，教师通常要根据习题的具体情况和针对学生数学习题训练中反映出来的理解偏差、普遍的问题、典型错误等对习题进行讲解，以达到帮助学生理解题意，清理思路，解决问题的目的。一直以来，我认为讲解习题就是把自己知道的、最好的、最多的、最精彩的、最与众不同的、最有体会的东西，用直接、明了、简捷、完整的方式交给学生。然而，教学实践证明并非如此。

新课改已经明确指出：教学中学生是主体，教师是主导，教学应该重视学生的体验和困难，把课堂时间有针对性的放到解决学生困难，突破学生思维受阻点这个“刀刃”上。古人推崇教育“授之以鱼不如授之以渔”，在教学上，老师们也一直在努力达到“授之以渔”的目标。

小学高段年级学生已具备了一定的数学知识和学习能力的储备。教师完全的“授之以渔”，就会忽略了学生的亲身体验，忽视了学生的困难，还不如“佐之而渔”。把课堂还给学生，教师只在其中组织、引导、合作，让学生自己去发现、去探索、去解决，以最小的知识代价，引起学生最多的思考。下面就结合小学高段数学教学中一些实践经验，谈谈如何对小学数学习题进行有效讲解 ，让“习题讲解”成为一个不可多得的有效数学教学资源。

一、日常生活中，体验和理解数学

“数学的根源在于普通的常识”。儿童在日常的生活实践中也有许多有意识的经验活动，并通过这种活动形成了许多的日常“经验”或“概念”，在这些经验和概念里，不乏蕴含和数学相通的知识、朴素的数学思想方法和解题策略等。在指导学生解决数学问题时，教师如能唤起儿童的这些日常“经验”或“概念”，帮助学生搭建数学与生活的桥梁，必将有助于促进学生对数学的深刻理解，解题策略的有效生成和问题解决能力的提高。

【案例】一幢大楼有15层共42米，小平家住6楼，她家地板到地面有多高？

（人教版六年级上册《分数除法》练习九）

学生第一次碰到这个数学问题，大多是这样计算的：42÷15×6=16.8米。这说明学生不通过有意识的经验活动，也就不能形成具体的经验概念。针对具体的数学习题，有必要激发学生的生活经验，让学生在明白生活事理过程中，去经历、体验数学，主动地获取自己需要的数学知识。在反馈前，我先引同学们一起“站”在一楼楼梯口，“这地面是几楼？”。又补充了一个问题“她家天花板到地面有多高”，同学们恍然大悟。

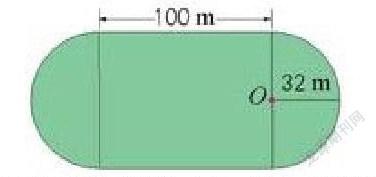
【案例】一个运动场如右图，两端是半圆形，中间是长方形。这个运动场的周长是多少米？（人教版六年级上册《圆》练习十六）

这个“操场模型”可以说是“圆”一章中比较典型的题目，学生往往连同左右两条直径也加上。有学生还理直气壮得提出：那两条直径不是实线表示的吗？应该加上去！我问学生，你们还记得今天早上晨跑了吗？那咱们是从哪出发，跑到哪算是一圈呢？你有把铅球场地边的那两条直径也跑上了吗？学生们摇摇头，一个学生似有深悟道：“老师问得对，再说了，“周长是多少米”，指的是操场一周的长度，不走回头路的。如果我们400米比赛，我们肯定跑这条路线，哪还会把那两条直径也搭上呀，那不是亏大了！”同学们听了呵呵笑了，相信这笑声的背后蕴藏着他们对这个题目的真正理解，老师的一问加上学生的再释，把全班学生又带回现实操场中去溜达了一圈，从而让学生感受到成为情境中的主人，去亲身体验也是解题的一个策略。

用生活的事理来引导学生理解数学，启发学生生成解决数学问题的策略，在数学教学中其实很多，借用“曹冲称象”的故事来教学转化的解题策略，用超市里购物发票来学习单价、数学量和总结的关系等等。

二、矛盾思辨中，完善认知结构

数学是研究数量关系和空间形式的科学，数学学习的本质是以数学知识为载体促进学生思维的发展。“学习”不是简单的信息积累，是新旧知识、经验的相互作用，及由此而引发的认知结构的重组，而这个重组，离不开“思辨”。矛盾后的思辨是学生认知发展的源泉，又是思维发展的基础。

皮亚杰认为，学习是一种通过反复思考招致错误的缘由、逐渐消除错误的过程。因此，学生解题中出错是学习活动的必然现象，对于解题中出现的错误与疏忽，我不仅要看到其消极的一面，而且更要看到这是提高学生解题能力、完善认知结构的一个极好机会。教师应该养成利用学生的错误提高数学教学的能力，加强数学教学效果的习惯，把学生的错误看作可以充分利用的有效课堂教学资源。

美国著名发展心理学家盖耶有句名言：“谁不考虑尝试错误，不允许学生犯错误，就将错过最富成效的学习时刻”。在上面的教学案例中，正是因为学生错误的出现，才给全班带来一次有意义的讨论，进一步完善了学生的认知结构。！

三、实践操作中，探索和创造数学

新的课程标准早已指出动手实践、自主探索是学生学习数学的一个重要方式。小学数学教材中的习题素材是紧密联系学生的生活实际来选取得。但学生在生活中如果没有留心的观察，有意注意，往往是“熟视无睹”，很少有学生会从数学的角度，带着数学问题去观察思考和研究的生活中的事物和现象的，因此经常是“素材很熟，却毫无感知”。

【案例】有一个花坛，高0.5米，地面是边长1.3米的正方形。四周用砖砌成，厚度是0.3米，中间填土。（1）花坛所占的空间有多大？（2）花坛里可以填多少立方米泥土？（人教版五年级下册《长方体和正方体》习题卷）

虽然学生每天经过学校大门口的花坛，体育课集会前在坛边玩玩坐坐，但很多学生就是想不出计算花坛容积的方法。于是我就把全班学生分成几个测量小组，每个小组优中差学生合理搭配，到旁边体育办公室借了测量工具，组织学生开展以“测量学校花坛所占空间和能填多少土”为主题的测量活动。在学生的动手操作中，探索出了“花坛所占空間”与“能填多少土”的计算方法，并感受了这两个问题的不同之处，获得了解决此类问题的经验。

可见，实践操作是学生获得感性知识发现数学关系的重要途径，只要我们在课堂上给学生创造合作探索的机会，放手让学生操作，真正把学习的主动权还给学生，相信学生的潜能能得到充分的发挥，个性得到发展。在这以上活动中，实践操作起了很大的作用。通过自己亲手实践得出的结论，记忆特别深刻，学生学习兴趣也就油然而生，创造能力得到发展，习题讲解更显有效，教学质量则更有提高。

四、拓展交流中，走向深刻思维

讲解作为教学的一种形式，也不能是教师一个人的独白，它也应是师生之间，生生之间的交往互动与共同发展的过程，它需要对话和交流。有效的习题拓展与交流可以促进学生间的众多信息相互碰撞交织，使学生的思维由表层走向深入，沟通数学知识之间的联系，促进学生数学思维的发展。

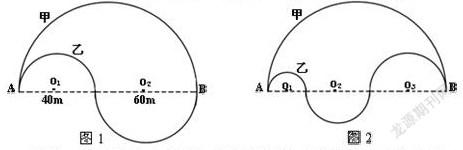
【案例】人民公园景点A与景点B之间有两条路线（如图1），小明想从景点A到景点B去，他选择哪条路线比较近？

“圆的周长”教学中经常采用的一道应用性问题。在实际教学中，学生大多能主动运用所学知识，分别计算两人从A点到B点的具体路程：S乙=3.14×（40+60）÷2=157米，S乙=3.14×40÷2+3.14×60÷2=157米;进而比较得出结论：两条路径长度相等。

显然，其结果的获得具有很强的条件（具体数值）依赖性，而且所得结论也从属于特定的具体情境。因此，我们教师应引导学生从所得的具体结果或结论出发，展开类比、猜想、验证等一系列思维活动，建构出具有相对独立性和普遍意义的数学模式，实现数学结论从特殊向一般的自然过渡与提升。上述问题结果或结论可以这样拓展：（1）类比猜测：（如图2）人民公园景点A与景点B之间有两条路线，小明想从景点A到景点B去，他选择哪条路线比较近？与原题相比，乙路线构成由两个半圆周长向三个半圆周长拓展，这种数量上的增加使问题具有一定程度的拓广性（在汉语语境中，“三”具有“多”的意涵）;而且，题中未给出半径的具体数值，迫使学生以一般化方式思考与处理问题，实现思维方式的转换。这个过程首先在四人小组讨论交流，说说自己有何建议。（2）检验论证：在学生根据前问题解决作出类比猜测“两条路径长度相等”后，教师引导学生寻求数学依据，验证猜测的可靠性：L甲 =πd/2 =π（d1+d2+d3 ）/2，L乙 =πd1/2+πd2/2+πd3/2 ，根据乘法分配率，π（d1+d2+d3 ）/2=πd1/2+πd2/2+πd3/2，即L甲 = L乙。

数学是关于模式的科学，它们所反映的已不是某一特定事物或现象的量性特征，而是一类事物或现象在量的方面的共同特征，因此数学模式相对于现实原型而言具有更为普遍的意义。因此，在实际问题解决教学活动中，我们不能就题论题，讲解完此题就以为万事大吉，我们不能满足和停留于问题具体结果或结论的获得，而应充分利用所得出的结果，努力去引出一般的结论，揭示其内在的依据，并作出可能的推广，让习题在拓展与交流中，实现“讲解”的真实本质，让学生的思维一步步走向深刻之处。

五、锦囊妙计中，感悟数学魅力

爱因斯坦说的好：想像力比知识更重要，因为知识是有限的，而想像力概括着世界上的一切，推动着进步，并且是知识进化的源泉。在解决实际问题的教学中，一般都十分注意运用分析法、综合法、分析—综合法等一般方法来帮助学生理解题意，整理解题思路，但一些特殊的问题，就需要有特殊的策略或方法，特殊的解题技巧，这样往往更容易促进学生对数学问题的理解，对问题的解决，同時可以让学生感受到数学的奇妙，数学思想方法的魅力，增强学生数学学习的情趣，提高他们解决数学问题的能力。

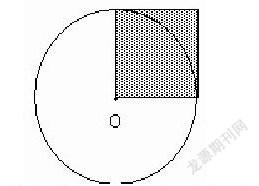
【案例】已知图中正方形阴影面积是10平方厘米，求这个圆的面积是多少平方厘米？

这道题中，学生能想到圆的半径长度和正方形的边长相等，若根据阴影10平方厘米求出正方形边长，圆面积便可求得。但是根据六年级所学知识还求不出正方形的边长具体是多少。但可指导学生运用“设而不求”的方法来解决，设正方形的边长是R，那么R×R=R=10平方厘米，由此可得S=3.14×10=31.4（平方厘米）。

数学的魅力就在于其思维的挑战性。在学生思考问题“百思而不得其解”时， 取出一些“锦囊妙计”，把难题变易，让学生有“柳暗花明”、“豁然开朗”的感觉，感受数学的神奇，获得积极的情感体验，往往就能把学生引进数学的殿堂，踏进数学探究的大门。

苏霍姆林斯基说过：在人的心灵深处，都有一种根深蒂固的需要，这就是希望感到自己是一个发现者、研究者、探索者，而在儿童的精神世界中，这种需要则更加强烈。作为一线数学教师，我们更应小心呵护和发展孩子的这种“需要”。特别是在习题的训练讲解中，激发学生用眼去观察、用手去创造、用脑去思考、用心去体会，“佐之而渔”，那时我们会惊奇地发现：孩子们笔端涓涓流出的不再是枯燥乏味的数字、符号，而是他们的智慧、个性和快乐的心境。

参考文献：

[1]吴正宪.《小学数学课堂教学策略——师生互动共同创建有效课堂》[M].北京师范大学出版集团.北京师范大学出版社.2010年6月.

[2]郑俊选.《小学数学教学改革实践与研究》[M].人们教育出版社.2003年8月.

[3]李烈.《我教小学数学》[M].人们教育出版社.2003年8月.

[4]《小学数学教师》.上海教育出版社.2009第11期.2010第7期.

[5]《教学月刊》.2010.7-8小学版.