“双减”背景下的初三数学复习“一题一课”
2022-06-09朱虹宇
朱虹宇

摘要:在初三复习阶段的后期,学生即将迎来人生第一次大考——中考,正是因为中考的重要性和紧迫性,在初三后期学生大部分的学习都会集中于对过去三年所学初中知识的综合复习,但是鉴于总体知识的庞杂系统性,尤其是数学课程复习的困难性,教师在教学的过程中,往往要应用更为科学的复习学习方法,以此提高学习效率减小复习压力,促进学生的数学复习知识掌握,结合当前双减背景之下对学生学习减负的要求,因此在教学的过程中,很多教师就应用了一题一课这一方法,这也是本文研究分析的主要目标所在。
关键词:双减;一题一课;数学复习
一题一课是指在教学的过程中,通过对一道典型例题或学习材料的深入研究实现有效教学的方法,这种教学方法不但能够实现对数学课程教学内容的完成,更容易实现教学过程中对学生数学学习能力、思维能力、学科素养等各方面的深入教学和培养,促进学生的进步发展。也正是因为一题一课在教学过程中的提纲挈领的带头性作用,以及学生学习过程中的梳理归纳价值,当下的一题一课教学在应用的过程中具备广泛的应用基础,不但在普通课程教学中可以应用,在复习课程的教学中也可以应用,而基于其教学方式对学生的有效进步发展作用,一题一课也符合双减政策和背景对学生的要求。
1.理性回归课本,梳理数学概念
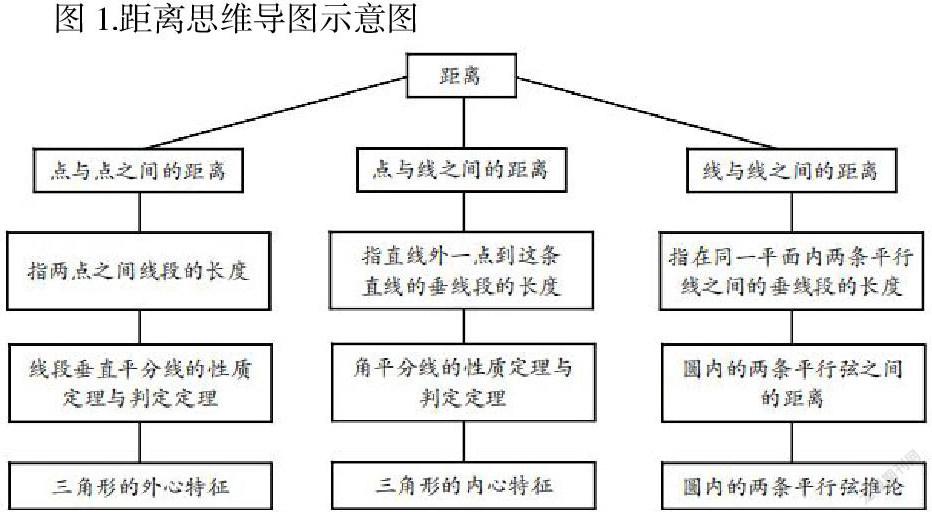
在双减背景下,初三数学复习一题一课的教学,首先应当注意对课本的回归,对于课本的回归主要是为了更好地进行数学学习中理论知识的梳理和掌握,因为一方面理论知识是一切数学实践的基础,学生只有掌握了书本上理论知识的基本内容,才可以实现有效的实践内容学习。另一方面则是在教学的过程中,学生更为稳固的掌握数学理论知识,可以减少在教学过程中对理论知识的学习,也就可以更好的推进其他数学课程学习内容的教学,由此一来学生可以从繁杂和往复的数学理论中抽身,减少自身学习压力,实现对双减政策的支持。而对于理论的学习,以距离这一重要教学内容为基础,教师在教学的过程中可以引导学生进行距离相关理论概念的寻找,包括“两点之间的距离”概念、“直线外一点到直线的距离”概念、“平行线间的距离”等,并且将这些概念理论串联在一起,在结合生活的情况下进行距离含义的理解和叙述,紧接着教师就可以引领学生联想与之相关的概念,包括垂直平分线的性质、角平分线的性质、三角形外心内心等,最终让学生通过思维导图的绘制和学习实现对理论知识的串联,思维导图具体如图1所示。
2.画图叙事,运用图形直观辨析数学概念
画图叙事就是在学习中,通过对图形的绘制进行事件的叙述和知识的理解,这种方法相对于其他学习方式更为直观,能够让学生学习过程中以更快的速度和效率理解,符合双减政策对学习学习的新要求,也比较契合一题一课复习教学对快速复习和知识重温的要求。例如,在进行距离相关知识的复习中,教师就可以通过引导学生画图进行距离的感知,包括两点之间线段长度、点到直线的距离是指点P到直线的垂线段的长度、平行线间的距离是指一条直线上的任意一点P到另一条直线的垂线段的长度等,如此可以让学生较快的复习线段与垂直线的含义功能,实现对相关概念和含义的明确。
紧接着,教师还可以引导学生对三角形外接圆、内切圆的绘制,感受外心、内心的形成过程以及不同特征,然后学生根据同一平面内两条平行线的距离解决圆中两条平行弦之间的距离问题,进而能得出圆中两条平行弦所夹的弧相等的推论。如此一来,通过画图和亲手绘制,学生对于概念的理解会形成一个过程性思维,不再是对概念知识的死记硬背。
3.叙事画图,在问题中加深对数学概念的理解
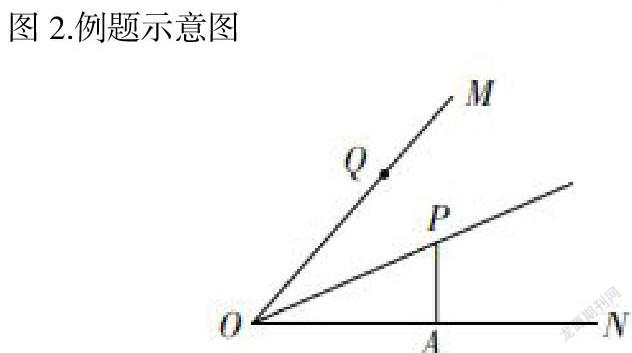
在双减背景下的初三数学复习一题一课中,教师要更多的注重对图形语言的应用,因为图形语言在数学教学中,相对于文字语言和符号语言具备更高的直观性,并且在特定内容的教学中,可以起到对教学内容的有效辅助。因此在遇到复习过程中的数学问题情况下,教师要正确引导学生进行图形的绘制,并且结合图形进行问题的分析解决。例如,如图2所示,∠M、∠O、∠N被点OP之间平分,并且PA⊥ON落于A点上,射线OM上存在一个为Q的动点,在假设PA=2的情况下,问如何求得PQ最小值。
对于这一问题教师在教学的过程中,应当注意首先引导学生做好对题目的分析,并且通过画图直观的发现,最小值只有在PQ为垂线的情况下才会出现,从而实现对问题的明确认识,以及用角平分线的性质定理求出PQ最小值,最終结果为2.
4.融合数学活动,增强数学概念的应用性
双减背景下初三数学复习教学中一题一课的教学应用,还需要注意在教学的过程中融合数学活动,注重对数学概念应用性的增强。因为在现阶段的初中数学教学和中考题目中,数学活动的占比越来越大,在中考教学中平移、翻折、旋转灯都是重点和热门的考试问题,因此教师对初三复习教学的引导,要注重注意对相关数学活动的引入应用,以此促进学生中考经验的积累。而这就要求教师在教学的过程中,注意引导学生学习应用数学概念进行问题的解决。例如,徐州中考数学就曾经考到这样一道题,如图3所示,将边长为6的正三角形纸片,按照图示的顺序进行两次折叠,展开后得到折痕得折痕AD、BE,点O为其交点。根据题目求如下问题,(1)对AO、OD的数量关系进行探求并对理由予以说明。(2)如下图4所示,当BE、BC上各存在P、N两个动点,那么当PN+PD的长度取得最小值时,求BP的长度。(3)如图5所示,如果BO线段上存在点Q则BQ=1,求QN、NP、PD相加的最小值。
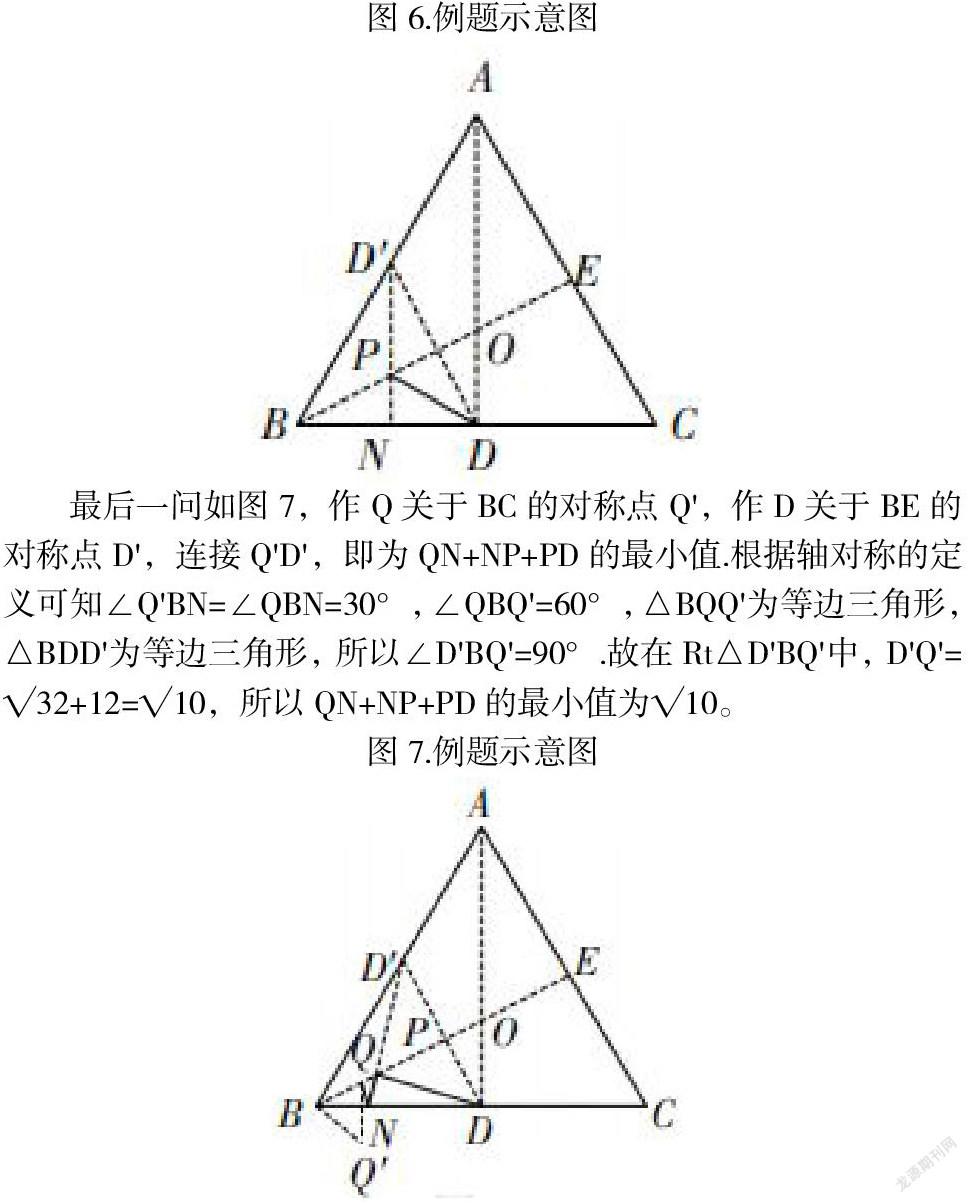
对于这一问题的解答,很多学生只能对(1)小题进行解答,但是对于后续问题却往往不知所措,这是主要是因为后续问题多了折叠活动和翻折变化,因此很多学生由于复习不到位或掌握不完善就导致难以求解,造成失分。而实际上对于这一问题,只要学生能够明白等边三角形的对称性,就可以实现对D点位置的确认。在接下来的过程中,教师就可以引导学生对动点P有限考量,作定点D关于动点P所在直线的对称点D',把PN+PD的长度最小值转化为PN+PD'的长度最小值,再转化为求D'N的最小值,如图6示,从而转化为点与直线的最短距离求得PB=√3.
最后一问如图7,作Q关于BC的对称点Q',作D关于BE的对称点D',连接Q'D',即为QN+NP+PD的最小值.根据轴对称的定义可知∠Q'BN=∠QBN=30°,∠QBQ'=60°,△BQQ'为等边三角形,△BDD'为等边三角形,所以∠D'BQ'=90°.故在Rt△D'BQ'中,D'Q'=√32+12=√10,所以QN+NP+PD的最小值为√10。
结语
综上所述,在双减背景下的初三数学复习一题一课中,教师的教学要注意借助一题一课的教学方式,进行相关教学内容的复习,在复习的过程中不但要注意对数学基础概念的教育,更需要注意教学过程中对画图教学的应用,因为图形语言相对于其他两种语言来说更为直观的反应几何中的位置关系与数量关系,除此之外,还有教师必不可少的板演展示,用于加强规范性培养,让初三学生避免“跳步骤”而出现逻辑漏洞的问题,这样子一题一课的推进教学模式来说能够更好地促进学生对知识的理解和概念的掌握、能力的螺旋式上升递进、学科素养的总体养成。总的来说是有利于教育教学工作稳步有序、递进式开展的。也有利于学生形成有条理、成系统的知识结构和严谨却又具有发散性的数学思维。
参考文献:
[1]程龙军,史承灼.基于“一题一课”的初中数学单元复习教学策略的研究[J].中学数学教学,2021(06):9-11.
[2]顾以成.探究学习模式下的“一题一课”[J].中学数学教学,2021(06):38-41.
[3]刘琴.探索“双减”背景下初中数学课堂的有效教学[J].新课程,2022(15):11-13.
[4]黄延久.中考视野下初中数学“一题一课”复习课教学策略[J].名师在线,2021(30):34-35.
