基于奇异摄动的柔性关节机械臂终端滑模控制*

付中乐，段洪君，骆 新，刘智康

(东北大学秦皇岛分校控制工程学院，秦皇岛 066004)

0 引言

机械臂在现代工业有着广泛的应用，其可以在不同的应用场景完成各种工作。在需要人与机械臂密切接触的场景中，轻量化的设计往往可以提升其安全性。然而随着重量的减轻，其控制问题却变得更加复杂，特别是关节中能量传递元件带来的关节柔性将显著影响控制效果[1]。因此在控制器设计的过程中应充分考虑关节柔性，不能将其忽略。SPONG[2]将柔性关节等效为线性弹簧，得到了柔性关节机械臂动力学模型，此后基于此模型的控制方法被广泛研究。现已提出的直接控制方法主要有反馈线性化[3]、滑模控制[4-5]、反步控制[6-7]等，这些控制方法均为基于四阶动力学模型直接设计，计算机仿真结果表明这些方法可以获得良好的性能。然而这些方法须将连杆角位移的三阶或四阶导数值准确反馈至输入端才能获得闭环稳定，实际工程中可通过对连杆角位移多次求导或通过模型转换为电机角位移及速度值获得，然而无论通过哪种方式都将受到建模误差和测量噪声的影响，产生较大偏差[8]。

为了避免求取连杆角位移高阶导数值，奇异摄动法提供了一种理想的解决途径，该方法可以将原四阶系统降阶为两个二阶子系统分别进行设计，仅需反馈连杆角位移和速度值就能获得闭环稳定，而且可以减少计算量，降低设计难度[9]。刘福才等[10]利用奇异摄动法对机械臂模型进行降阶处理并对二阶子系统即边界层系统设计了模糊PID控制律，虽取得了良好的效果却未考虑外部扰动和建模误差。夏杭等[11]在对柔性关节机械臂降阶系统进行设计的过程中虽考虑了外界扰动，并设计了滑模控制律以克服其影响，由于采用的是传统的线性滑模面，不能保证跟踪偏差在有限时间内收敛，其性能仍有提升的空间。

利用奇异摄动法设计的柔性关节机械臂控制系统性能提升的关键在于边界层系统控制律的设计。本文将非奇异终端滑模控制(NTSM)应用于边界层系统控制律的设计中，在传统NTSM的基础上[13]，设计了一种新型趋近律，有效提升了轨迹跟踪性能，同时通过设计自适应律解决了工程实际中扰动上界未知的问题。

1 数学模型和控制目标

1.1 数学模型

本文将一个由直流电机驱动且具有柔性关节的单连杆机械臂作为被控对象，柔性关节的动力学特性可利用具有弹性系数为K的线性扭转弹簧来近似表示，其结构如图1所示。

图1 柔性关节机械臂结构图

根据文献[5]的研究成果，同时考虑机械臂工作环境中存在的扰动，可以得到被控对象的数学模型为：

(1)

式中，q为连杆角位移；θ为电机角位移；I为连杆转动惯量；J为电机转动惯量；K为等效弹簧弹性系数；u为控制器输出即电机输入电压；d1和d2分别为作用连杆侧和电机侧的外部扰动；M为连杆的质量；L为连杆的重心与转子之间的距离。

1.2 控制目标

柔性关节机械臂的轨迹跟踪控制目标即为在任意初始状态下设计控制律使连杆的角位移q(t)与其参考值qd(t)的偏差快速收敛至0，实现轨迹跟踪。

2 模型降阶

首先利用奇异摄动法进行模型降阶，定义μ=K(θ-q)，K1=ε2K，其中，0<ε≪1，则式(1)可以写为奇异摄动形式：

(2)

(3)

(4)

(5)

设计边界层系统的控制律为：

(6)

得到边界层系统闭环运动方程为：

(7)

3 准稳态系统设计

3.1 扰动观测器设计

(8)

(9)

(10)

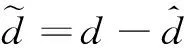
(11)

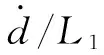
3.2 控制律设计

设计非奇异快速终端滑模面：

(12)

式中，e=x1-xd为轨迹跟踪偏差；λ1>0；λ2>0；1m/n。这种滑模面可以在避免奇异问题的前提下，使跟踪偏差在系统到达滑动模态s=0后由其初始值e(tr)≠0经有限时间收敛至e(ts)=0。

对式(12)求导得：

(13)

(14)

为了加快系统到达滑动模态s=0的速度，在文献[13]所做研究的基础上，设计一种新型趋近律为：

(15)

式中，k1>0；k2>0，σ(s)的表达式为：

(16)

式中，μ1>1；0<μ2<1，趋近律式(15)可重新写为分段形式：

(17)

为了实现式(15)的趋近律，设计降阶系统的控制律为：

(18)

式中，等效控制输入un为：

(19)

由于扰动观测偏差上界通常是未知的，设计自适应切换控制输入ur为：

(20)

(21)

3.3 稳定性证明

定义边界层系统的Lyapunov函数为：

(22)

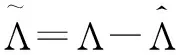
(23)

4 仿真分析

利用计算机搭建模型对控制系统进行数值仿真。参考文献[12]，被控对象的参数设置如表1所示。

表1 被控对象参数

为了验证本文所提方案对单连杆柔性关节机械臂的轨迹跟踪控制效果的优越性，分别设计PID控制律和基于奇异摄动的传统滑模控制律进行数值仿真与本文所提方案作对比，为了克服控制律鲁棒项中符号函数sign(s)不连续带来的抖阵问题，实际应用时采用连续函数θ(s)=s/(s)|+γ)替代之，其中γ为正常数。

所设计的PID控制律为：

(24)

(25)

三种控制器增益和参数如表2所示，这些数据均为经过多次试验获得最佳性能时所得到。

表2 控制器参数

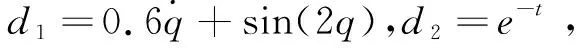
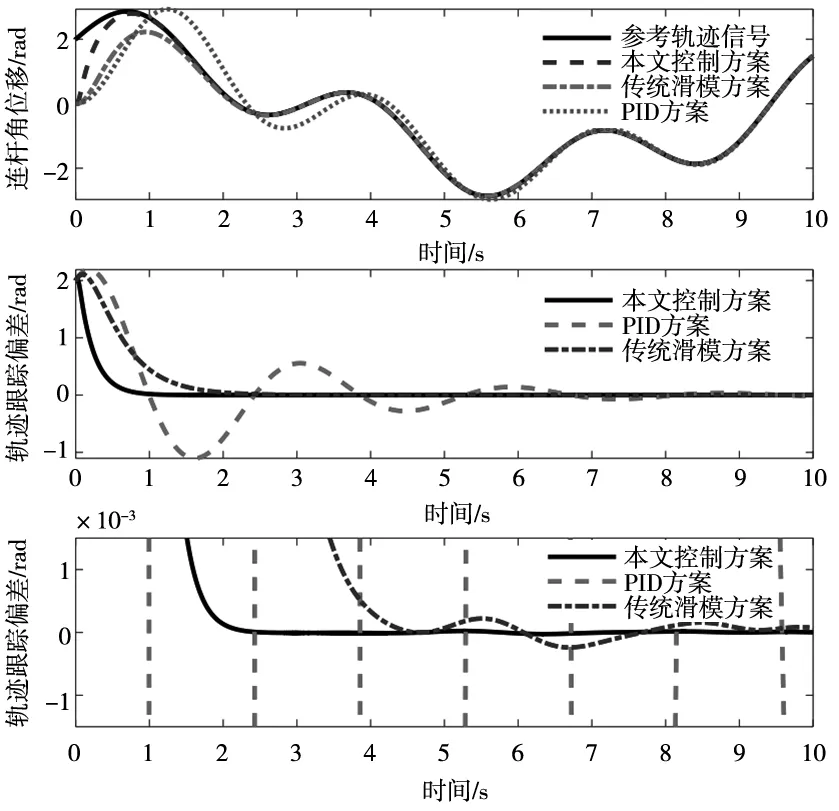
图2 轨迹跟踪效果及偏差图

如图2所示，相比PID方案和采用线性滑模面的奇异摄动方案，本文所提方案明显具有更良好的瞬态及稳态性能，能够以较快的速度实现轨迹跟踪且具有较小的稳定误差。定义平均跟踪偏差为：

(26)

式中，N为仿真时采样的次数；E的值越小，表明轨迹跟踪效果越好，三种控制方案的性能对比如表3所示。

表3 性能对比

本文所设计的扰动观测器估计出复合扰动，有效提升了整个系统的轨迹跟踪效果。实际扰动及其估计值如图3所示。

图3 扰动观测效果图

5 结论

本文建立了单连杆柔性关节机械臂的数学模型并利用奇异摄动法对其进行降阶得到二阶模型，降低了设计难度。对边界层系统复合扰动设计了扰动观测器，并将其应用至非奇异快速终端滑模控制律中。重新设计了一种新型趋近律有效改善了性能，针对扰动上界未知的问题，设计了自适应控制律将其有效解决。仿真分析也证明了本文所提方案的优越性。接下来的工作是将本文的控制算法进一步应用至实体机械臂上，验证其良好的轨迹跟踪性能。