LMD单道多层偏移堆积成形角度预测与控制*

鲁 俊，殷 鸣，谢罗峰，向 锦，李 伟

(四川大学机械工程学院，成都 610065)

0 引言

金属增材制造技术常被用来制造或修复一些薄壁零件，如发动机壳体、机闸、叶片等，这些构件往往不全是竖直薄壁形式，而常是倾斜的结构。要成形斜壁零件，可以预先或同时堆积出支撑结构以防止成形过程中发生坍塌，但是事后处理支撑结构却较复杂。因此对无支撑式成形的研究就显得极为必要。

目前，倾斜薄壁结构的研究已得到了国内外学者的广泛关注。运用金属增材制造技术制造倾斜薄壁件的无支撑成形方法整体分为三种[1]：打印头偏移堆积、打印头变姿态堆积、基板倾斜堆积。KAZANAS等[2]通过打印头变姿态法，使用经验过程控制模型通过CMT(cold metal transfer)工艺沉积了从垂直位置到水平位置的各种角度的墙壁。XIONG等[3]基于GMAW(gas metal arc welding)技术制造倾斜薄壁零件时，定义了成形层的倾角并通过调节送丝速度和行进速度来控制倾角大小。LAURA[4]在沉积具有较高斜率壁时，通过多种方法对比，发现打印头的方向平行于沉积壁的方向并垂直于基板表面的打印方式可以使零件几何变形最小。

面向燃烧室结构的圆形薄壁件，王续跃、江豪等[5-7]依据偏移不塌陷的临界条件和层高建立了成形倾斜角度数学模型，使用变Z轴提升量法对圆弧截面倾斜薄壁件进行熔覆成形。余超等[8]在给定工艺条件下，采用预设夹角的方式，最终成功获得了三元叶片样件。

现存的文献大多致力于极限倾斜角度的研究，而鲜有对于倾斜角度的成形精度控制的探索。本文基于实验，从数据层面研究了倾斜角度与重要工艺参数的对应规律，并设计了控制器加以控制，获得了较优的效果。

1 关键工艺参数对宏观倾角的影响探究及分析

1.1 实验材料和设备

本文采用打印头偏移堆积法，即保持打印头在竖直方向工作、层与层之间只进行水平方向上的微量偏移。采用的工艺是激光熔化沉积(laser melt deposition,LMD)，这是一种以激光为能量主要针对金属粉末材料进行成形的增材制造技术，成形过程中可以兼顾效率和性能，目前广泛应用于军工场合[9]。

实验中所用的材料为30CrNi2MoVA粉末，这是一种合金结构钢，所成形件具有高强度、冲击韧性良好等优点，常应用于军工装备制造中。选用的基板为Q235钢，尺寸为250 mm×350 mm×10 mm，实验前去除了基板表面的氧化膜，然后用乙醇擦拭并风干。本文涉及LMD装备主要由机器人、激光器、送粉器、集成打印头等几部分构成。

1.2 正交实验

LMD技术是以“离散-堆积”的形式层层堆积起来构件，所以构件整体的成形效果也是由微观上每层的成形效果叠加在一起构成的。根据已有的研究对倾角大小的定义，层高和偏移量对其有着最直接的影响，而层高又与能量输入密切相关，这里体现为激光功率、扫描速度等工艺参数[10-11]。因此对于激光功率、扫描速度和单层偏移量进行了初步研究，设计了三因素混合水平正交实验，每组组内实验参数不变，如表1所示。

表1 正交实验工艺参数水平表

实验得到了49组成形试件，沉积长度为80 mm，堆积层数为50层。成形件的侧壁整体趋向平行于一个平面，如图1a所示，根据打印头扫描方向将成形试件平均分成4段，以获得A、B和C三个截面，再通过金相显微镜对其进行角度测量，发现三个截面角度差距极小，最多不超过平均值的6%，所以取三个截面的平均值为整体宏观倾角。这里结合图1b 给出本文中宏观倾角的定义式如下：

(a) 恒定参数偏移堆积截面位置示意图

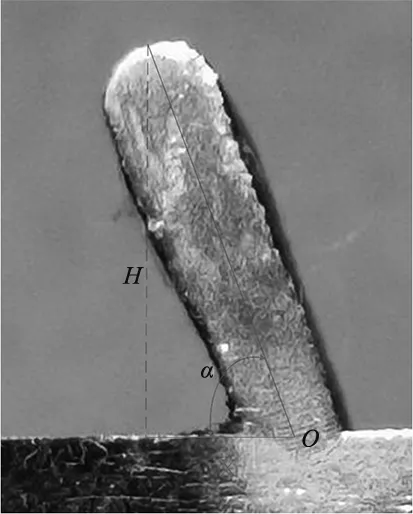
(b) 宏观倾角测量图1 恒定参数偏移堆积截面位置示意和宏观倾角测量示意图

(1)

式中，以试件与基板交线中点O为原点；α表示宏观倾角；H是试件最高点的高度；X是该点在水平方向上的投影长度。

1.3 线性回归建模及分析

根据测量结果，采用SPSS软件对激光功率、扫描速度与单层偏移量对宏观倾角进行回归分析，其结果显示这三个因素可以很好的预测成形件的宏观倾角，模型拟合度较好，模型的判定系数R为0.933，其线性回归模型为：

α=-0.002P+1.043V+182.973Δx-6.055

(2)

式中，P是激光功率；V是扫描速度；Δx是单层偏移量。

将原本的工艺参数代入回归模型中，可以得到该工艺参数下的预测值，并将预测值与实际值进行对比，发现两者有较好的一致性，如图2所示。

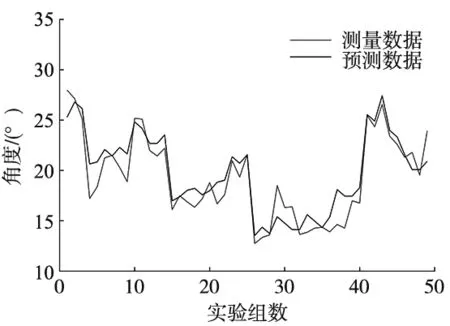
图2 线性回归模型效果比较

根据得到的线性回归模型，扫描速度和单层偏移量的回归系数都大于零，表示与宏观倾角呈正相关，激光功率的回归系数为负数，表示其与倾角呈负相关。这可以从能量输入的角度和倾角的几何定义角度方面说明。LMD偏移堆积过程粉末熔融的能量输入来自于激光所带来的高热量，其他因素不变情况下，激光功率越高则输入的能量就越高，熔融的粉末量就越多，成形层的高度也就越大，整体高度也就越高，根据倾角的几何定义式可知倾角会越小；扫描速度越快则单位时间内的能量输入越小，因此成形层的高度越小，同理分析得知倾角会越大；单层偏移量越大则试件总体在水平方向上的投影越长，倾角也会因此更大。

极差分析法是正交试验结果分析最为常用的方法，其原理是计算极差Rj来判断因素对试验结果的影响程度。其中，Rj反映第j列因素波动时的试验结果的变动幅度，Rj越大则表示该因素对试验结果的影响越大。计算公式如下：

(3)

通过计算，3个因素的极差R值如表2所示。可见对成形件宏观倾角影响最大的因素是单层偏移量，其次是扫描速度，最后才是激光功率。因此本文接下来针对单层偏移量进行了研究，并进行了层间的参数模型辨识以便控制成形件的倾角精度。

表2 不同影响因素的极差值

2 单层偏移量对层倾角的规律研究及其控制

对于单道多层偏移堆积过程成形的零件来说，倾角是一个重要的几何特征，其成形精度的保证十分必要。并且很多情况下宏观倾角还不是一个恒定值，而是随着层数在逐渐变化。所以为了使零件倾角达到目标值左右，需要对每层的倾角进行控制。所以本节辨识了层倾角动态特性模型以便设计合理的控制算法，保证控制系统的性能指标满足要求。

2.1 辨识信号设计

为确定输入信号—单层偏移量的变化范围，经过对恒定参数实验结果观察，选择基本工作点为激光功率1600 W，扫描速度8 mm/s，光斑直径3 mm，送粉器转速1.5 rpm，单层偏移量为0.14 mm。系统辨识对输入变量的最低要求是必须对系统过程的所有模态进行激励，同时又不可以使堆积过程发生“坍塌”，经过综合考虑选择单层偏移量的变化范围为0.05～0.3 mm，变化步长为0.05 mm。由于是层间控制，即每一层反馈一个角度值，由堆积长度80 mm得采样周期为10 s。生成了输入信号的随机时间序列信号，如图3所示。经过偏移堆积实验得到了有61层的试件，将其切开后研磨、抛光、腐蚀，利用显微镜测量其层高，再根据已有的对层倾角的定义[4]将其除以已知对应的单层偏移量再取反正切函数计算出倾角大小，显微测量图和测得的2-60层倾角数据组成的辨识信号分别如图4a和图4b所示。

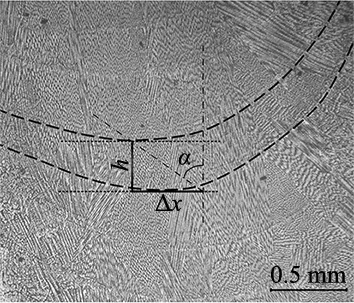
图3 层倾角示意

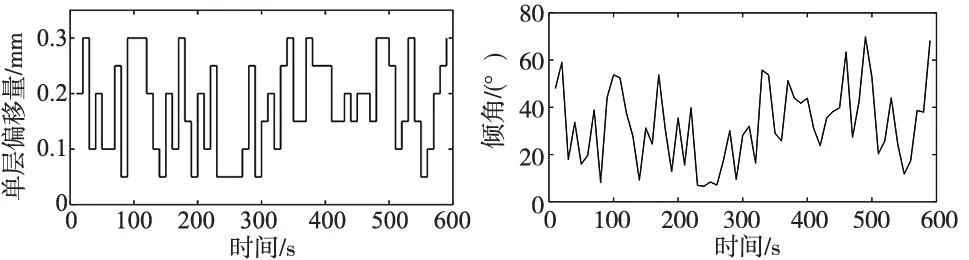
(a) 输入信号 (b) 输出信号图4 系统辨识的输入输出信号

2.2 动态系统辨识

单道多层LMD过程是一个非线性且存在时变和时滞的复杂过程，简单的线性模型难以精确描述，必须建立合适的非线性动态模型。同时，单道多层LMD堆积是一个复杂的热、力、流体等多场耦合的过程，前面若干层堆积层都会对后面的层产生对应程度的影响，即需要根据历史时刻和当前时刻的信息去预测将来时间点的状态。所以初步经过对模型类别影响拟合度的筛选，决定使用的模型为非线性自回归模型(NARX)。同时使用线性自回归模型(ARX)进行辨识作为对照组。

NARX模型使用非线性和线性块的并行组合来描述非线性结构。非线性函数和线性函数被称为回归量，并通过根据指定的模型顺序对测量的输入和输出信号执行转换来计算回归量。回归量可以是延迟输入和输出，也可以是输入和输出的非线性函数。对于本文的NARX模型，采用标准回归量，即过去的输入量和输出量。用于预测当前输出的过去输出项和过去输入量的数目分别采用3和2；从样本数来看输入到输出的延迟，在本文中经过寻优确定为0。

(4)

式中，x(t)表示回归量；F是一个非线性回归函数，它用非线性估计器逼近，在本文中对于输出使用wavenet，其单元数则由工具箱自寻。图5显示了模型的预测输出是如何由输入和输出构成的。

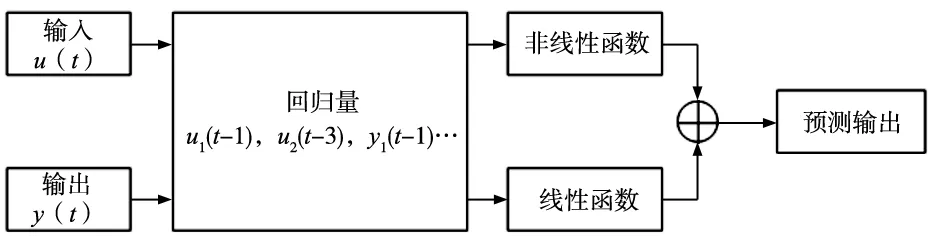
图5 非线性自回归模型结构示意

利用训练数据集和测试数据集验证了模型的有效性，最后模拟输出的拟合效果比较如图6所示。

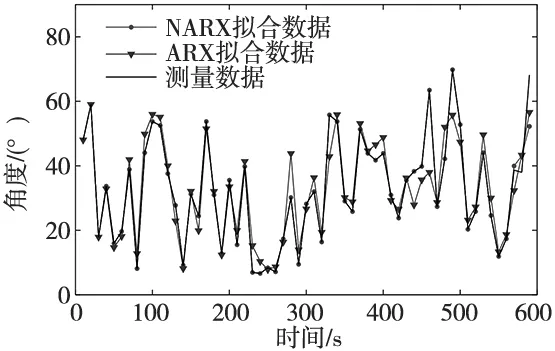
图6 系统辨识模型的拟合效果比较

辨识的拟合度结果相比较，NARX的是86.65%，ARX的是63.53%。可见用NARX拟合得更接近实验测量值，因此下文设计控制器的基础就是NARX模型。

2.3 控制器设计

单道多层LMD过程是一个非线性且存在时变和时滞的复杂过程，采用传统PID控制算法极可能满足不了其控制要求，往往需要动态调整PID的参数，而模糊控制正好能够满足这一需求。本文采用的模糊PID控制系统在Simulink软件里如图7所示。先预设一个角度值，通过反馈回来的实际值作差得出偏差以及微分计算得到偏差变化率，将其送入控制器中，控制器经过相应算法实时的给出需控制的单层偏移量，经由辨识出的LMD系统模型模拟仿真出一个仿真值作为实际值反馈到控制器前端形成一个闭环回路。

图7 模糊PID控制系统框图

本系统的模糊控制器采用Mamdani型，它将层倾角的偏差E和偏差变化率EC作为输入，通过模糊规则库对模糊化的输入量进行模糊推理，反模糊化后得到3个参数Kp、Ki、Kd送入PID控制器中，来实现对辨识出模型的闭环控制。

经过对系统的综合分析后，确定了5个量的论域、7个模糊子集和各变量的三角隶属函数。再由PID控制原理和参数整定经验，制定了Kp、Ki、Kd相应的模糊整定规则来使系统具有最佳响应性能。

在Simulink专业软件里搭建好各模块进行动态性能仿真，得到了较好的结果，同时补充了传统PID控制作为对照组。其中模糊PID控制器的3个参数Kp、Ki、Kd的变化如图8所示，基本都是在经过一阵大幅度震荡后在一个稳定值上下波动。预设目标值与最终控制值的比较如图9所示，先预设一个30°的角度值，在第300 s时突变为35°，模糊PID控制效果曲线能更好地追踪到目标值，通过对局部视图的观察，可见在第80 s即第9层左右达到了预设值，其稳态误差不超过0.3%。

图8 Kp、Ki、Kd的变化曲线 图9 层倾角控制曲线

3 结论

针对单道多层LMD偏移堆积工艺过程，本文进行研究并得到了以下结论：

(1)获得了成形件宏观倾角与3个工艺参数的对应规律，扫描速度和单层偏移量与宏观倾角呈正相关，激光功率与倾角呈负相关，其中最大影响因素为单层偏移量，扫描速度次之，激光功率影响最小。

(2)针对单层偏移量单因素影响，对层倾角变化规律进行了系统辨识，在两个模型中选择了更好的非线性自回归模型，其拟合度达到了86.65%。

(3)针对第(2)步中辨识出的模型设计了模糊PID控制器和传统PID控制器，结果显示模糊PID控

制跟踪效果更优良，在第9层跟踪上预设值，稳态误差不超0.3%。