管道超声导波检测缺陷周向定位数值模拟

李忠虎，李靖，王金明，李刚

（1. 内蒙古科技大学信息工程学院，内蒙古 包头 014010；2. 内蒙古自治区光热与风能发电重点实验室，内蒙古 包头 014010）

管道运输是现代工业极为重要的运输方式之一，广泛应用于石油、化工、冶金、电力及城市供水和供气等诸多行业，在国民经济中发挥着越来越重要的作用。随着管道的长时间运行，因材料腐蚀、介质磨损和外力作用等因素的影响，管道泄漏事故时有发生，故对管道缺陷检测技术进行研究具有重要意义[1-2]。管道缺陷检测方法有多种，相比其他检测技术，超声导波检测技术可以实现管道远距离的检测，适用范围更广，并且具有更高的检测效率，拥有其他管道检测方法不可比拟的检测优势，故得到了广泛应用，超声导波已成为目前管道缺陷检测领域的研究热点。

目前，对超声导波的理论和超声导波在管道中的传播特性的研究已比较成熟[3-6]，但是在管道缺陷的定位方面仍需进行深入研究，尤其是缺陷的周向定位。有限元法是求解复杂数学问题最有效的方法之一，是管道缺陷超声导波检测方法研究的重要工具，对管道缺陷的准确识别具有重要意义。WANG X.等[7]提出利用复合磁化的方法同时检测管道的周向以及轴向缺陷。YAN S.等[8]采用有限元软件对损伤管道结构进行数值模拟分析，利用基于PZT 的超声导波能量法对管道腐蚀缺陷进行研究，分析回波得出反射系数与缺陷径向深度的关系。蔡刚毅等[9]通过ANSYS 数值模拟对管道的周向缺陷进行定位，并利用最小二乘法拟合缺陷尺寸与导波反射系数之间的关系得出相应公式。CHEN B.等[10]利用压电陶瓷传感器对管道进行缺陷检测，提出了一种新方法（TOAIP）对管道缺陷进行二维定位。陈乐等[11]利用阵列式磁致伸缩导波检测管道缺陷，对多通道信号收集并进行逆向调制，实现缺陷的周向定位。

为了实现管道的健康监测和缺陷修复，管道缺陷的准确定位就显得十分重要。本文利用ABAQUS有限元软件对管道缺陷超声导波检测方法进行数值模拟，重点研究了管道缺陷的周向定位问题，介绍了能量幅值法和圆轨迹曲线法两种管道缺陷周向定位方法，并对实验结果进行了对比分析。

1 管道中的超声导波特性分析

管道中的超声导波具有多模态特性和频散特性，这是超声导波自身的独特性质。管道中的超声导波会在传播过程中产生多种导波模态[12]，不同的激励会产生不同的模态。而导波在管道中传播时，也会发生频散，这是导波传播过程中波速随频率变化而变化产生的一种现象。通常情况下，对管道缺陷进行检测过程中，需要根据导波的波动方程[13]计算导波在管道中的传播模态，然后根据Disperse 软件绘制的频散曲线选择相应的导波模态对其进行缺陷检测。根据导波遇到缺陷会产生反射、透射及模态转换等特性可以对管道缺陷进行定位。

由弹性动力学理论可以计算得到空心圆管中导波传播的频散方程，并且可以得到导波传播的频散曲线。如图1 所示是外直径为206 mm，壁厚为3 mm的钢管中的导波频散曲线。

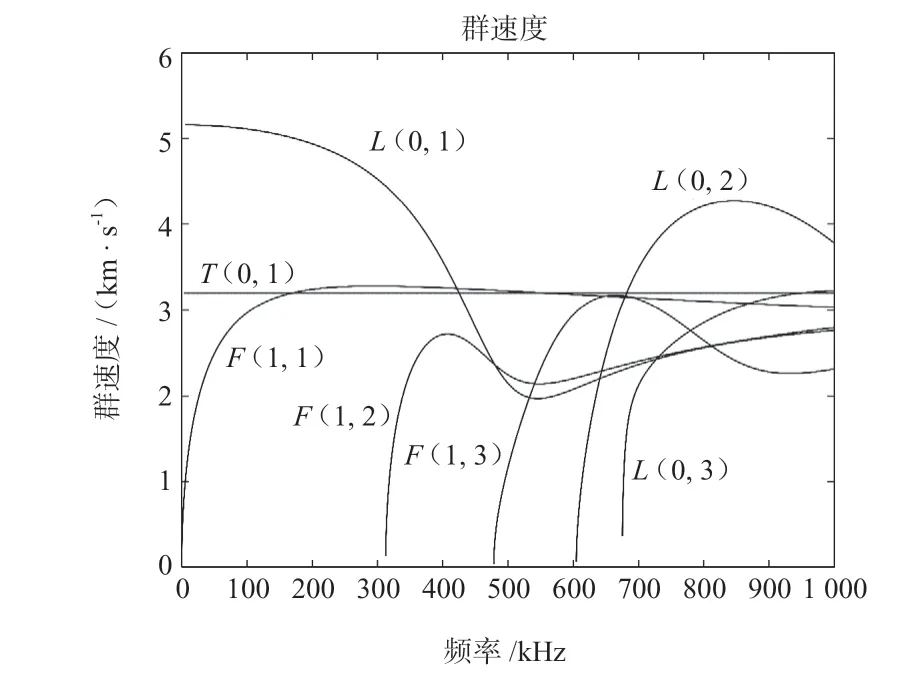
图1 钢管中导波的频散曲线Fig.1 Dispersion curve of guided wave in steel tube

从频散曲线可以看出，导波在管道中产生了三种不同的导播模态，分别是纵向模态、扭转模态和弯曲模态，在低频阶段有L（0，1）、T（0，2）、F（1，1）三种模态，群速度相对稳定的是纵向模态以及扭转模态，本文选用L（0，1）模态的导波进行数值模拟，具体选用35kHz 的导波频率，传播群速度为5 153.40m/s。

2 管道超声导波数值仿真参数设置

2.1 建立仿真模型

ABAQUS/standard 模块可以实现动力学显示分析，利用有限元软件ABAQUS 建立直管道模型进行有限元分析。如图2 所示，建立长度为2 m、壁厚为3 mm、直径为206 mm 的管道模型，管道材料选用Q235，属性为密度ρ= 7 850 kg·m-3，弹性模量E= 210 GPa，泊松比μ= 0.27。

图2 ABAQUS 直钢管模型Fig.2 ABAQUS straight steel pipe model

使用ABAQUS 中的part 功能模块设置缺陷，本文研究周向角度分别是30°、60°、90°、120°的缺陷的周向定位，缺陷的轴向宽度为2 mm，径向深度为1 mm，缺陷位置设置在距离激励端面1 m 处，30°缺陷的截面图如图3 所示。

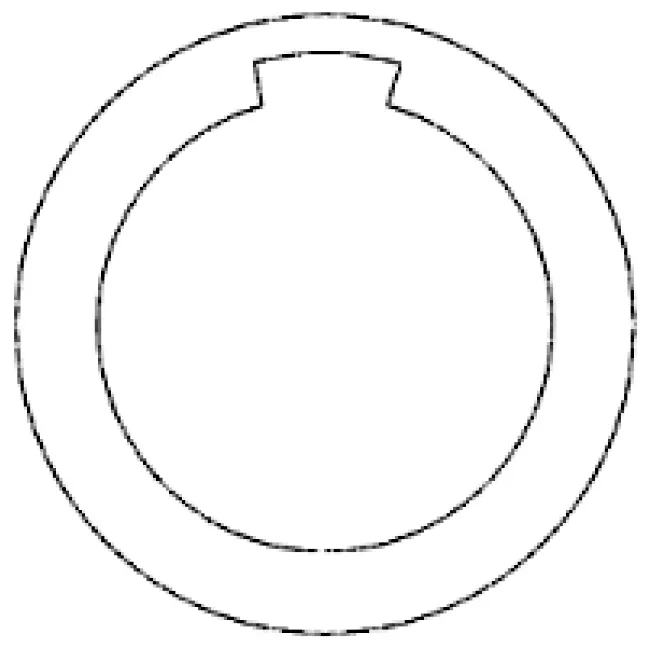
图3 30°缺陷的截面图Fig.3 Section of 30° defect

为了提高管道数值模拟的准确性，管端均匀加载8 个集中力激励载荷，载荷之间的夹角为45°，激励加载如图4 所示，8 个激励同时加载信号。

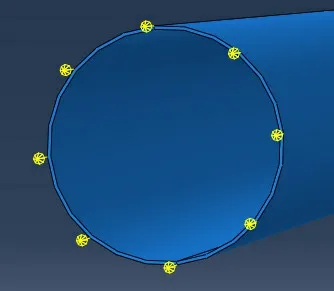
图4 模拟钢管缺陷截面Fig.4 Simulated steel pipe defect section

2.2 激励信号的参数设置

根据图1 可知，L（0， 1）在低频阶段频散较弱，可用于管道缺陷的检测。端部施加经过汉宁窗调制的激励信号：

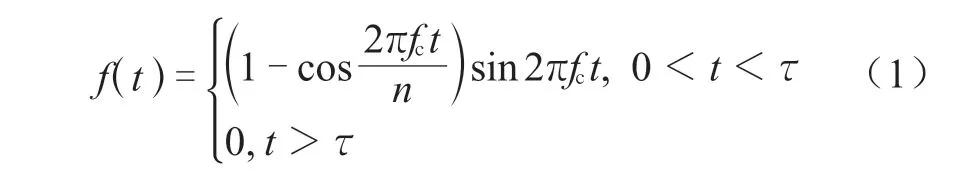
式中n——脉冲周期；

fc——中心频率；

τ——信号脉冲宽度，τ=n/fc。

本文选用中心频率为35 kHz 的10 个周期的汉宁窗调制信号，如图5 所示。

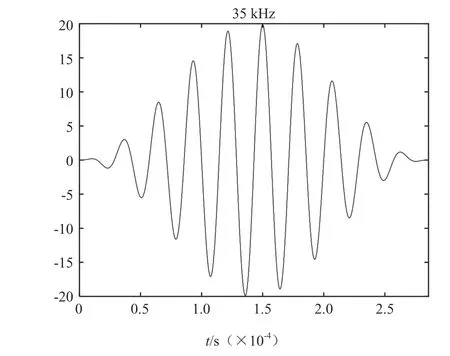
图5 汉宁窗调制信号Fig.5 Hanning window modulation

2.3 网格划分以及边界条件设置

采用ABAQUS 有限元分析软件实现管道数值模拟，为了使结果更加精确，网格划分以及边界条件的设置就显得尤为重要。根据波的传动效应，一个波长传播方向至少有10 个单元，网格单元长度l需要满足：）

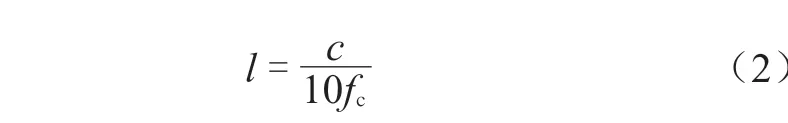
式中，c——导波速度；

fc——中心频率。

网格单元长度取1.5 mm；采样时间间隔为0.3 μs，无缺陷管道部分使用结构化网格划分，单元类型为六面体单元C3D8，缺陷部分使用自由网格划分，单元类型为四面体单元。管道截面网格划分分为两层，单元厚度为1.5 mm，如图6 所示。

图6 ABAQUS 钢管网格划分Fig.6 Mesh generation of ABAQUS steel pipe

管道边界条件的设置关系着计算结果的准确性，管道末端需设置成全固定方式，将管道的内壁和外壁固定5 个自由度，使得波在管道内部更好地传播。本模型是建立在基于管道外部理想的真空条件，便于后续导波对管道缺陷检测的周向定位研究。

3 管道缺陷损伤定位

利用超声导波对管道进行缺陷检测，要比钢板中的缺陷定位复杂得多，不仅要对管道缺陷进行轴向定位，同时还要确定缺陷的周向位置，从而确定管道的损伤部位。管道中超声导波传播的群速度较为恒定，计算公式为：

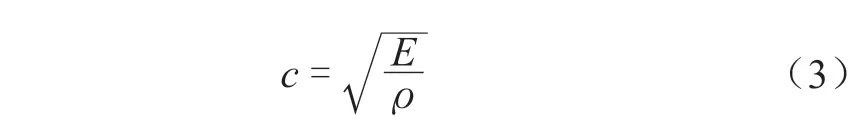
式中E——杨氏模量；

ρ——钢管密度。

本文的管道数值模拟是在管道一侧激发激励信号，并且在激励信号一端设置信号接收点，模拟信号的自发自收方式。

3.1 管道缺陷轴向定位

管道缺陷的轴向定位是通过对接收信号进行相应计算得到的。如图7 所示，能清晰看到激励波、缺陷回波和端面回波，可以通过三种波的接收时间计算其在管道中的传播速度，进而确定缺陷的轴向位置。取激励波的波峰时间t1为177.9 μs，缺陷回波的波峰时间t2为588.3 μs，端面回波的波峰时间t3为962.7 μs。

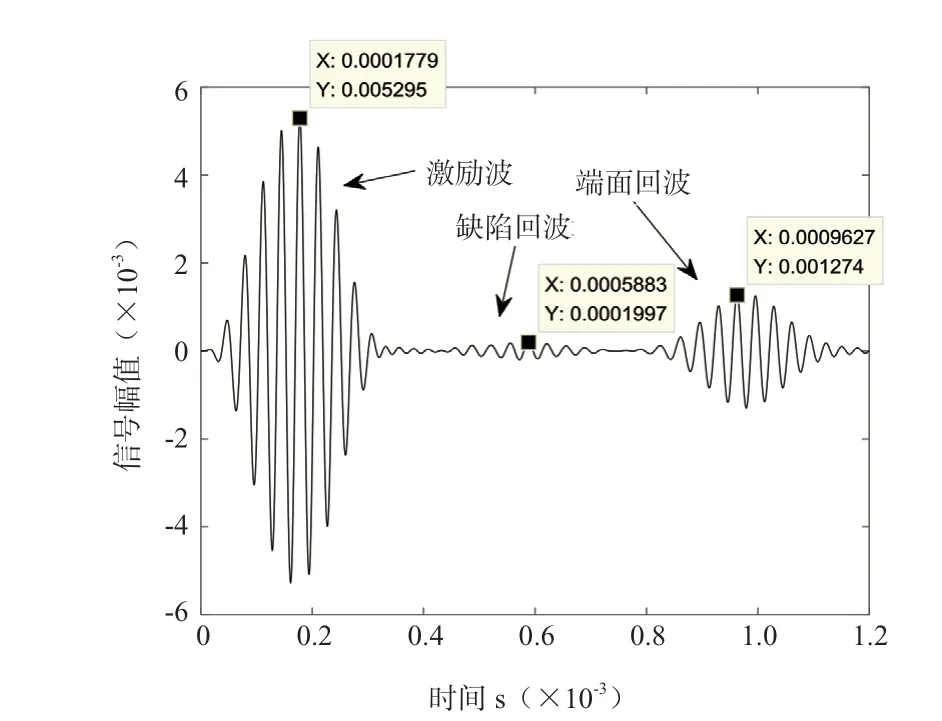
图7 钢管中缺陷回波信号时域图Fig.7 Time domain diagram of defect echo signal in steel pipe

信号传递时间t=t3-t1= 784.8 μs。导播传播速度v=s/t= 5 096.84 m/s。缺陷距离接收点的距离s= （t2-t1） ×s/t= 1 045.87 mm。

缺陷轴向位置在1 045.87 mm 处，与实际的1 000 mm 偏差45.87 mm，相对误差为4.59%，比较准确的定位缺陷的轴向位置。

3.2 管道缺陷损伤系数周向定位

损伤差异系数（损伤指数）可以用来判别管道采集信息的损伤程度以及包含的缺陷损伤程度。损伤差异系数的公式表示为：

式中D——损伤指数；

I（t）——管道无缺陷采集的信号；

V（t）——设置管道缺陷采集的信号；

t0——采集信号开始的时间；

t1——采集信号结束的时间。

利用损伤差异指数对管道缺陷进行周向定位，需要在圆周向位置添加多个传感器用以接收回波信号，利用各传感器接收到的缺陷回波幅值计算损伤差异系数确定缺陷的周向位置。

使用ABAQUS 建立的仿真模型，在一端设置8个信号激发点，并且在激发端一侧均匀设置25 个接收点模拟传感器接收回波信号，可以获得25 组回波信号数据，对25 组数据利用MATLAB 绘制在三维坐标图中，如图8 所示。可以看到图中包含了激发波、端面回波以及缺陷回波，明显看出不同周向的缺陷回波幅值有所差异，利用MATLAB 对25 组数据提取各自的缺陷幅值，并绘制周向极坐标图，可以确定缺陷的圆周向位置。

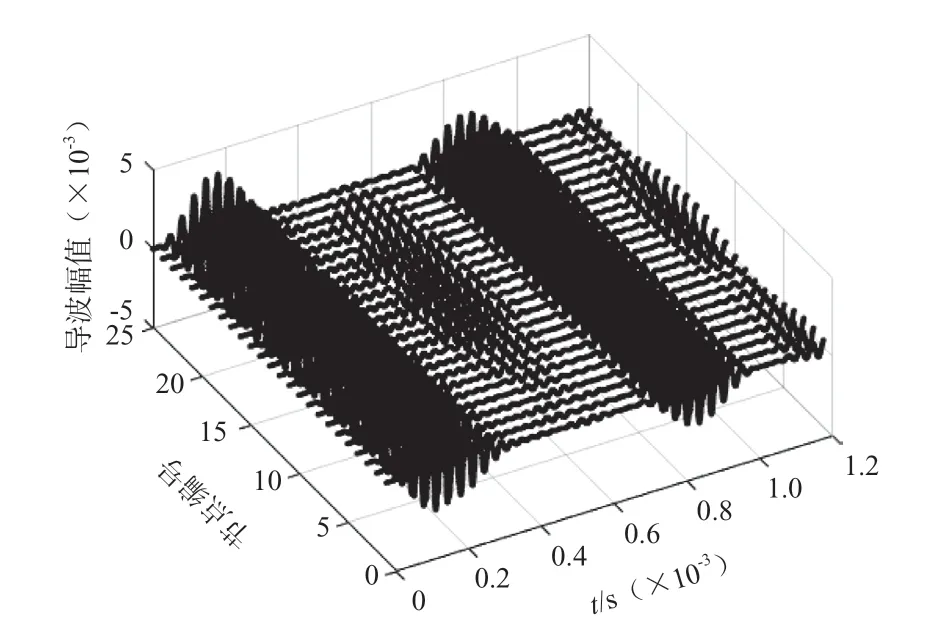
图8 缺陷信号三维展开图Fig.8 Three dimensional expansion of defect signal

利用计算缺陷损伤系数方法分别模拟了周向角度分别是30°、60°、90°、120°的缺陷，绘制周向极坐标图，分析此方法的周向定位可行性。四种周向缺陷的极坐标图如图9 所示。

由图9 可知，采用缺陷回波计算损伤系数绘制的极坐标图可以大致看到缺陷的周向位置，由于采集数据以及节点选取误差等原因，精确定位缺陷的周向位置还存在一定误差。

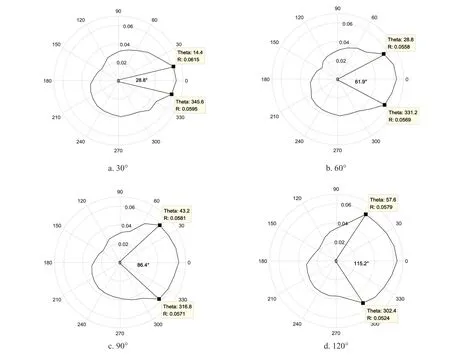
图9 不同周向角度缺陷的极坐标图Fig.9 Polar coordinates of defects with different circumferential angles

3.3 管道缺陷圆轨迹曲线法周向定位

管道中的导波向前传播都是沿着直线进行传播的，所以每个激发点激发的波都能到达缺陷并发生发射和透射，反射波继续沿着直线传播，可以到达接收点。管道中的8 个激发点相当于激励波有8 条导波沿着管壁传播，所以导波传播路径是8 条沿着管壁的曲线，将管壁展开成为平面，可以将导波传播路径的曲面问题转为平面问题，每个激发点的波到达缺陷并返回的路径长度有所差距，利用各导波轨迹相交的特点可以对缺陷进行周向定位。

管道的激发点和接收点位于同一端，位置固定，缺陷位置与激发点和接收点的相对距离固定，那么导播传播路径可以视为缺陷到各接收点的相对距离，可以以接收点为圆心，相对距离为半径，绘制8 条不同半径的圆轨迹曲线，8 条曲线必然会在一定区域内相交，交点为缺陷所在位置。将管壁展开绘制曲线以及接收点示意图如图10 所示，其中A1 ～ A8 为8 个接收点，绘制8 条圆轨迹曲线，交于两点确定缺陷位置。

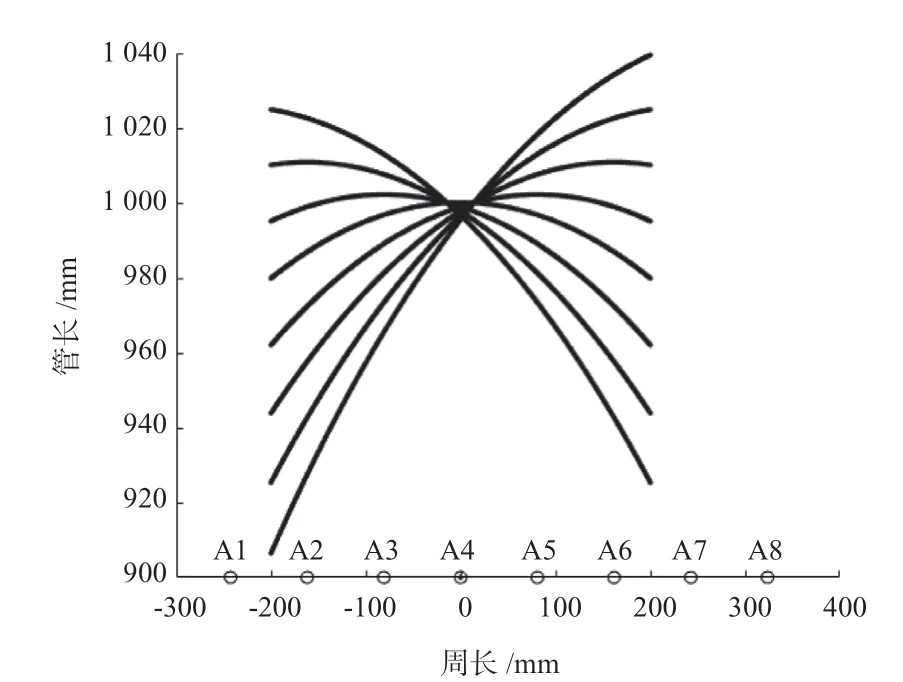
图10 圆轨迹曲线缺陷定位平面示意图Fig.10 Circular track curve defect location plan

在三维圆柱坐标系中，接收点位于Z= 0 mm 的平面上，接收点的坐标为（x0，y0，0），缺陷反射点未知，定义反射点坐标为（x1，y1，z1），信号接收点的角坐标为θ0，未知反射点角坐标为θ1，坐标变换公式为：

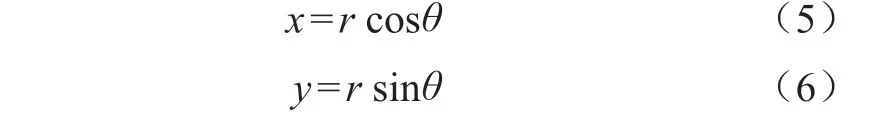
式中r——三维圆柱底面半径，r= 103 mm。

接收点与缺陷的相对距离s 的计算公式为：

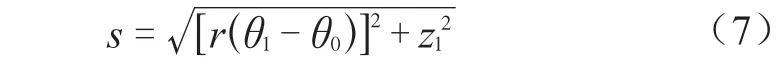
接收点的角坐标θ0= [0，0.25 π，0.5 π，0.75 π， π，1.25 π，1.5 π，1.75 π]，接收点分布如图11 所示。相对距离s由表1 计算可得，根据绘制圆轨迹曲线的理论，由计算得到的数据以及公式，便可绘制8 条圆轨迹曲线。

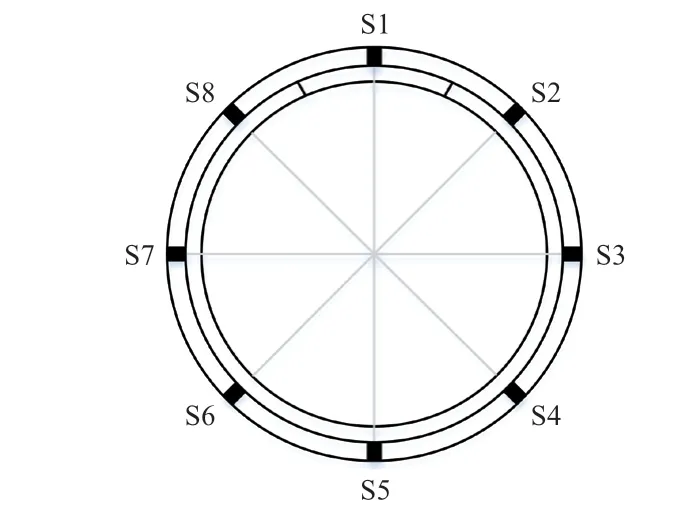
图11 传感器分布Fig.11 Sensor distribution

利用MATLAB 将8 条圆轨迹曲线进行坐标变化，绘制在三维圆柱表面，可以在圆柱表面看到拟合的管道缺陷，分别对圆周角为30°、60°、90°、120°的缺陷进行圆柱表面的圆轨迹曲线拟合。

有限元分析软件ABAQUS 建立圆周角30°的缺陷管道模型，经过有限元分析计算，采集接收点数据，经过计算各数据如表1 所示，圆轨迹曲线拟合缺陷如图12 所示。

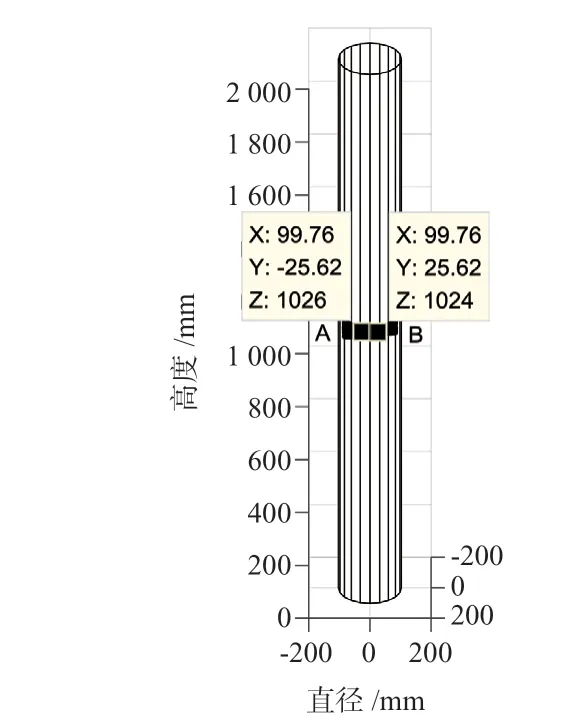
图12 30°缺陷的周向定位Fig.12 Circumferential location of 30° defects

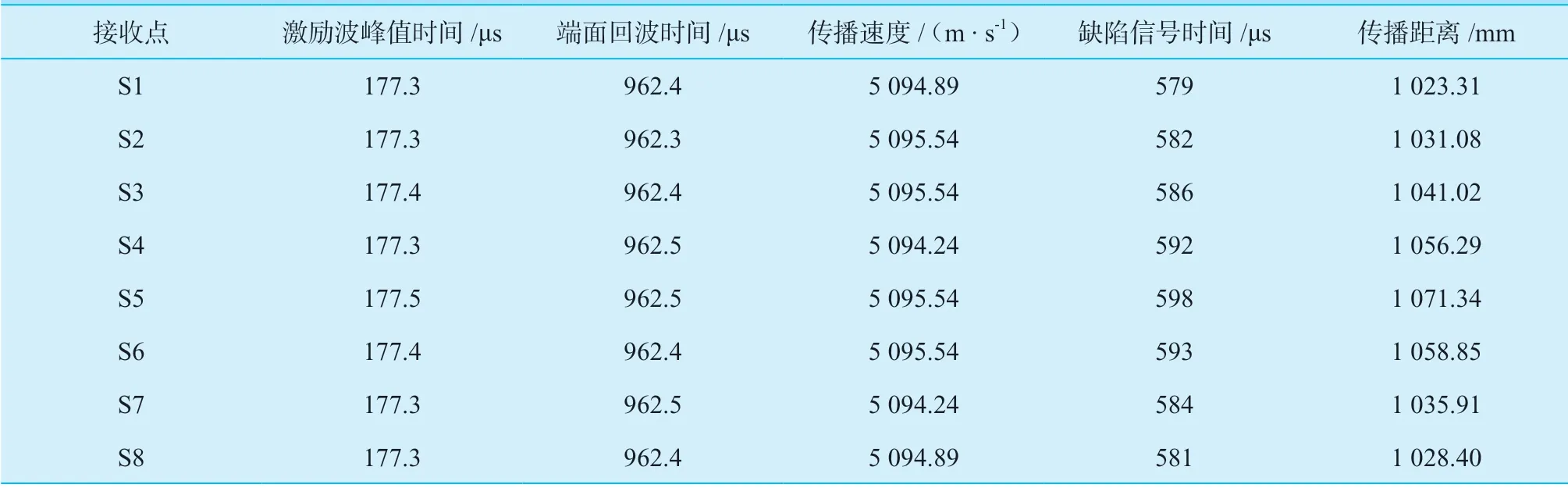
表1 导波信号传播速度与传播距离Table 1 Propagation velocity and distance of guided wave signal

经过MATLAB 绘制圆轨迹缺陷图像，缺陷两端的交点分别为A（99.76，-25.62，1024），B（99.76，25.62，1 024），经过坐标变换后分别为：A（103，-14.40°，1 024），B（103，14.40°，1 024），两 点 角度相差28.8°，与实际的30°缺陷相差不大，误差为4%，缺陷位置位于-14.40° ～ 14.40°之间，可以对圆周向位置进行定位。

为了验证此方法对圆周向定位的可行性，又分别对其他圆周角缺陷模型进行仿真分析，各缺陷周向定位的角度误差如表2 所示。

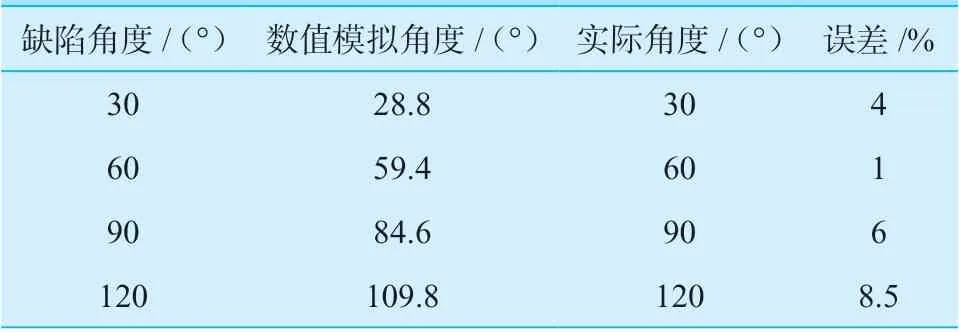
表2 缺陷圆周角误差分析Table 2 Error analysis of defect circumferential angle

通过利用圆轨迹曲线法对四种角度缺陷进行周向定位，发现缺陷角度的大小会影响周向定位精度，缺陷角度为60°时定位精度最高，随着缺陷角度的增大则定位精度降低，缺陷角度为120°时定位精度最低，为8.5%。

4 结论

本文针对管道超声导波检测中的缺陷周向定位问题，采用ABAQUS 有限元软件对四种不同角度的周向缺陷进行了数值模拟，然后利用损伤系数法和圆轨迹曲线法对管道缺陷进行周向定位，并对两种方法进行了分析和比较。研究结果表明，采用管道缺陷损伤系数法只能大致确定缺陷的周向位置，定位精确度不高；而采用圆轨迹曲线法则可以较好地对管道缺陷进行周向定位，并且角度较小的缺陷精度较高，总体缺陷定位精度在8.5%以内。