中心开孔法兰盖结构参数优化分析

郝明涛， 江保全，李宗伟，张杰，吴强

（1. 西南化工研究设计院有限公司，四川 成都 610225；2. 合肥通用机械研究院特种设备检验站有限公司，安徽 合肥 230031）

中心开孔法兰盖是压力容器中的一种典型零件，广泛应用于变压吸附领域的吸附塔、脱硫塔、脱氧器、脱萘塔等填料塔。这类设备的上封头中心位置通常需要设置人孔，并通过中心开孔法兰盖过渡到工艺管 口。

对于高温、高压、疲劳，介质易燃易爆或毒性程度较高的工况，开孔法兰盖补强通常采用带锥颈部结构，如图1 所示。开孔法兰盖尺寸确定时一般采用等面积补强法进行设计，等面积补强法应用简单，但应用于疲劳工况的开孔法兰设计时有明显不 足。

等面积补强确定的结构尺寸，对法兰盖开孔边缘的二次应力的安定性问题是通过限制开孔几何尺寸间接加以考虑的，而未对开孔边缘的峰值应力问题加以考虑。因此，等面积补强无法计算出开孔法兰盖应力强度最大值，从而确定的结构尺寸不能直接用于疲劳工况，此其缺点一。

图1 模型开孔率≤0.5，采用等面积补强法时，开孔附近兼做法兰的整体锻件未对开孔区域的补强作用加以考虑。模型简化为平盖进行分析，补强具体方式为：增加接管厚度、整体增加平盖厚度或两种方式组合[1]。这种粗放式的调节方式，尤其是整体调整法兰厚度补偿开孔面积，往往使得法兰盖重量显著增加，经济性欠佳，此其缺点二。

综上所述，对于高周疲劳工况，无论从安全性，还是从经济性角度，都有必要对中心开孔法兰盖结构优化设计进行深入探讨。

1 模型分析

以某项目变压吸附制氢工段吸附塔顶部中心开孔法兰盖为研究对象，如图1 所示。开孔法兰盖与NB/T 47023—2012 FM PN4.0 DN 500 标准法兰配对使用，中心开孔经锥颈过渡后与φ168.3 mm×11 mm的管道相连。模型中有5 个待定参数，分别为：δ、N、θ、r、R。下面就来探讨这5 个结构参数对中心开孔法兰盖的影响。

主要设计参数见表1。

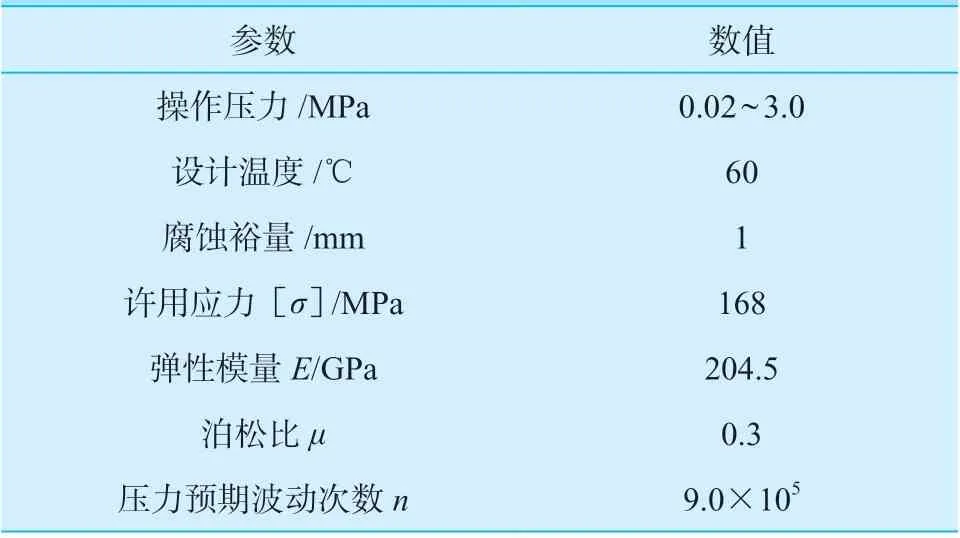
表1 设计参数Table 1 Design parameters

忽略螺栓孔对法兰盖刚度的削弱，不考虑法兰盖接管端弯矩、扭矩等外载荷，即仅考虑内压、垫片反作用力以及管口轴向拉力对模型的影响。简化后的模型载荷和几何结构上具有轴对称特性。为加快迭代速度，采用2D 模型中Plane183 单元对模型进行网格划分[2]，对锥颈区域通过“element size=3 mm”进行加密处理，2D 模型边界条件如图2 所示。

图2 模型边界条件Fig.2 Model boundary conditions

2 变量与优化目标

为保证中心开孔法兰盖的经济性与安全性，优化目标分别为：模型横截面积S（对于轴对称模型，用横截面面积表征质量）；应力强度最大值σmax；法兰盖密封面最大形变量Δy。结构优化设计的数学模型如下[3]：

式中 [σ]—— 疲劳工况对应的许用应力强度值最大值，MPa；

[Δy]—— 保证开孔法兰盖密封特性的允许最大位移，见图3，mm；

A——法兰盖模型中待定结构参数定义域。5 个待定结构参数为设计变量，其数据见表2。

表2 变量数据Table 2 Data of variable parameters

图3 为简化后密封面与法兰盖几何尺寸关系图，由图可得式 （1）。

图3 许用位移计算模型Fig.3 Calculation model of allowable displacement

法兰密变形为微小变形，即α→0，故而式（1）简化为式（2）

按照保证密封面转角≤0.3°[1]，中心开孔法兰盖密封面许用位移[Δy]为：

[Δy] = （D/2 -d/2）（0.3×π /180） ≈ 1.3

根据表1 设计参数，查标准中疲劳曲线[4]，限定最大应力强度值[σ]≤170 MPa。

3 中心组合试验

采用ANSYS Workbench 中的“Response Surface”模块，对优化目标参数进行中心组合设计实验，试验样本点包括一个中心点，输入变量轴的端点，以及水平因子点[4]。对于中心法兰盖优化模型，5 个变量对应27 个样本点，实验数据见表3。

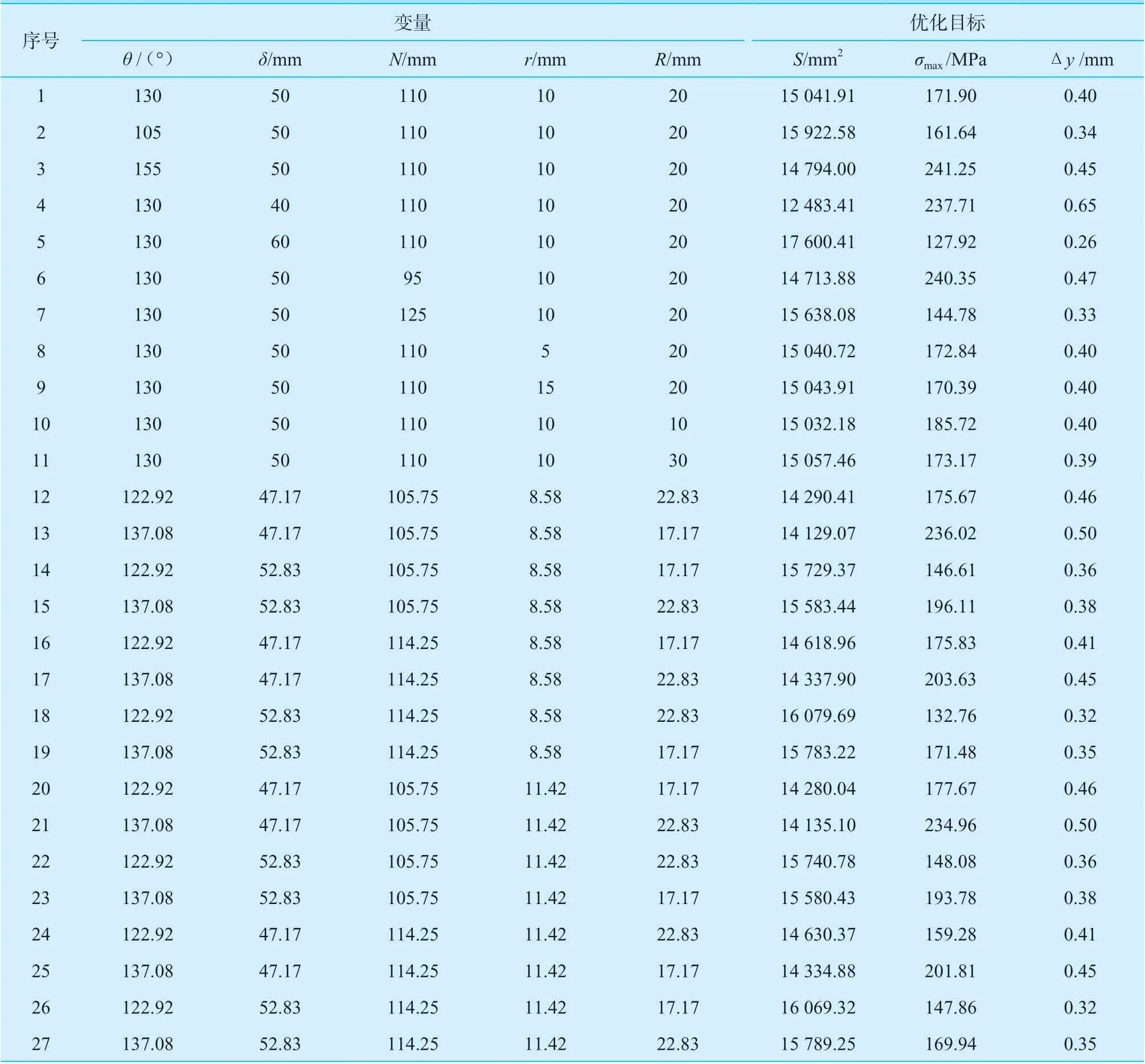
表3 中心组合设计实验数据Table 3 Data of central composite design

4 参数敏感度及响应曲线

4.1 参数敏感度

对于法兰盖模型中心组合实验数据进行分析和处理，得到变量敏感分析图，如图4 所示。由图可知：

图4 变量对目标参数敏感度Fig.4 Sensitivity of variables to target parameters

（1）5 个设计变量中，相对于法兰盖厚度δ、锥颈大端半径N、锥颈角θ，锥颈大端圆角R和锥颈小端圆角r对优化目标参数S、σmax、Δy的影响可以忽略，即主要影响变量为δ、N、θ。

（2）3 个主要影响变量中，法兰盖厚度δ对优化目标参数S、σmax、Δy的影响最大。而且，目标参数S、Δy对变量法兰盖厚度δ变化的敏感度远远超过锥颈大端半径N和锥颈角θ，但δ、N、θ对于目标参数σmax的影响力相当。

（3）应力强度最大值σmax和密封面最大形变量Δy与3 个主要影响变量中的法兰盖厚度δ和锥颈大端半径N负相关，与锥颈角θ正相关，即增大δ、N或减小θ，σmax、Δy数值减小，反之亦然。

（4）法兰盖横截面积S与3 个主要影响变量中的法兰盖厚度δ和锥颈大端半径N正相关，与锥颈角度θ负相关，即增大δ、N或减小θ，S数值增大，反之亦然。

4.2 优化目标响应曲线

模型中设计变量δ、N、θ、r、R对应力强度最大值σmax、最大位移Δy、法兰盖横截面积S三个优化目标参数的响应曲线如图5 ～ 7。

图5 应力强度最大值对变量的响应曲线Fig.5 Response curve of maximum stress intensity to variable parameters

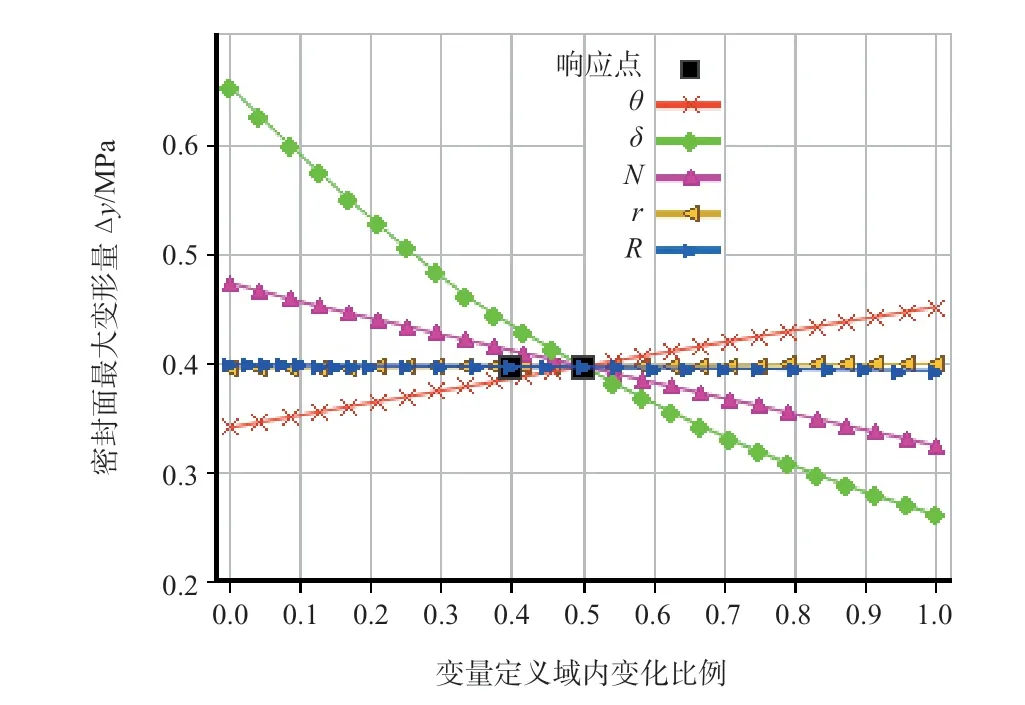
图6 最大变形量对变量的响应曲线Fig.6 Response curve of maximum deformation to variable parameters

图7 模型横截面积对变量的响应曲线Fig.7 Response curve of model cross sectional area to variable parameters

变量定义域内，曲线斜率越大表明对应变量对目标参数的影响越显著。曲线斜率为正，表明对应变量与优化目标数值正相关，反之亦然。

5 设计点选取

结合变量对优化目标的影响规律，以及中心组合试验数据表选取设计参考点。设计点选取的时候，考察的顺序依次为：刚度→疲劳→重量，即对应优化目标的顺序依次为：最大变形量Δy→应力强度极大值σmax→模型截面积S。

筛选条件1，根据法兰盖密封刚度要求，Δy≤1.3 mm，即表3 中的27 组尺寸组合均满足刚度要求。

筛选条件2，结合表1 疲劳工况要求，法兰盖的应力强度极大值σmax≤170 MPa。对表3 中有9 组数据满足要求，应力强度数值从大到小的试验序号依次为：27、2、24、22、26、14、7、18、5。

筛选条件3，横截面积最小即重量最轻。条件2筛选出来的9 组数据中，序号24 所对应的截面积最小，且影响权重最大的指标法兰盖厚度也是9 组参数中最小。因此，序号24 对应尺寸组合，为优化设计参考点，其参数如下：

X= （122.92，47.17，114.25，11.42，22.83）

结合敏感度及响应曲线对优化目标的影响趋势对数据进行微调，得到一组优化设计点X*，其参数如下：

X*= （120，48，115，10，20）

该设计点下应力云图和变形云图通过对称显示，如图8、图9 所示。

图8 最佳设计点应力云图Fig.8 Stress contour of optimum design point

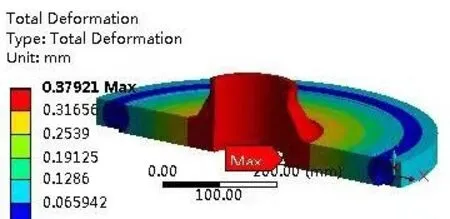
图9 最佳设计点变形云图Fig.8 Total deformation contour of optimum design point

对X*设计点对应模型网格进行再加密处理，设定锥颈区域 “element size = 2 mm”，在同样的边界条件下，模型应力强度最大值为162.7 MPa，最大变形量为0.379 2 mm。由此可见，优化计算时模型网格尺寸选择合理。

由图8 可知，高周疲劳工况下的开孔法兰盖，其最大应力值小于材料的许用应力强度，即法兰盖所有点均处于弹性变形状态，可以不再采用线性化方法对危险路径应力进行分类评定。

6 结束语

尽管厚度对法兰盖的刚度、强度、应力强度极大值的影响最大，但锥颈大端半径和锥颈角对法兰盖性能的影响不能忽略，而且往往能够通过这两个局部尺寸的调整，在保证法兰盖刚度和疲劳特性的同时，实现轻量化设计。

带锥颈的法兰盖宜采用锻造至法兰外形的毛坯制作，不仅可以提高锻件材料利用率，减少加工量，还最大程度保留了金属流线组织的连续性，能更好地保证法兰盖良好的力学性能[5]。此外，数值分析结果表明锥颈大端内外易成为中心开孔法兰盖高应力区，制造过程宜提高表面粗糙度要求，并加强质量检测。对于关键设备，建议零件图上对高应力区进行标识，精加工尺寸到位后，对高应力区进行100% UT + 100%MT，降低高应力水平区域萌生疲劳裂纹的风险。