积灰对光伏组件发电量影响及清灰周期规划*

张文帅 ，王 帅 ，邬 凯

（陕西工业职业技术学院，陕西 咸阳 712000）

我国西北地区具有丰富的太阳能资源，该地区太阳能辐射值高，全年晴天较多，为光伏发电产业的发展提供了有利条件[1]；但该地区荒漠化较为严重，也是我国沙尘暴高发区，该地区的气候特点使光伏组件积灰严重，使到达光伏组件表面的太阳光减少，造成光伏组件接收到的太阳辐射能减少，进而影响光伏组件发电量[2]。同时，使得光伏企业运行成本增加。

近年来，针对积灰对光伏组件发电量的影响国内外学者进行了大量研究。Jiang等[3]运用仿真法以不同闭合材料研究其性能的影响，推出随着积灰密度变化，其输出减少率同时变化。Hegazy[4]通过对室外以软件拟合推出积灰和透光率的关系。陈东兵等[5]进行立杆阴影室外实验，推出表面积尘与光伏组件的变化关系。Hassan等[6]对未清扫的太阳能输出板进行记录，得到相应时间效率变化关系。Darwish等[7]推出不同种类污染物及相关电能物理量的变化关系。李练兵等[8]运用软件建立数学模型，拟合出积灰密度与功率成反比关系。Sulaiman等[9]、Qasem等[10]、Pravan等[11]以及Mohamed等[12]结合理实一体化实验证明发电率与灰垢成反比关系。

沙尘呈非规律性遍布电池板表面，观测时间不同[13]，温度不同，观测结果同样受到很大影响。因此运用软件以灰尘沉积量和太阳能透光率的拟合关系对实际应用有着至关重要的作用。

本文在上述研究基础上，结合软件仿真模型，计算输出功率与光伏组件变化关系结构[14]，研究在两者之间的关系证实积灰密度的增大，功率呈一定范围降低，得到观测时间内的清灰周期。

1 光伏电池组件模型

光伏电池是指运用特殊材料遇光产生相应效应的器件，光伏电池的等效电路如图1所示。

图1中，Iph为光生电流；Id为二极管结电流；Rsh为并联电阻（阻值较大，数量级为103 Ω）；Rs为串联电阻（阻值较小，小于1 Ω）。

图1 光伏电池等效电路图

光伏电池是利用半导体材料的光电效应或者光化学效应，将光能转化成电能的装置。根据光伏电池等效电路原理[15]和Shockloy的扩散理论可得光伏电池的I-V方程：

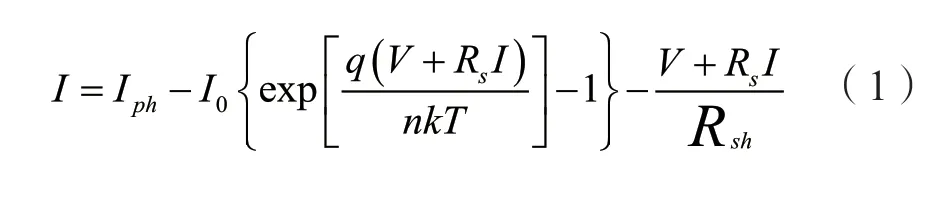
式中，I0为反向饱和电流（数量级为0.1 A）；q为电子电荷（1.6×10-19C）；n为二极管因子（取值范围1～5）；k为波尔兹曼常数（1.38×10-23J/K）；T为绝对温度。

实验中采用英利（YingLi Solar）能源有限公司的型号为YL260P-29b的光伏电池组件，主要参数如表1所示。

表1 YL260P-29b型光伏电池组件的主要参数

2 积灰对光伏组件发电量影响仿真分析

根据Adel A Hegazy[4]得到的灰尘沉积和透光率降低的拟合公式：

式中，τ为积灰光伏组件的透光率；τclean为干净光伏组件的透光率；erf(x)为高斯误差函数。

根据公式（2）可知，随着光伏组件表面积灰增加，光伏组件透光率降低，对光伏组件的发电量产生较大影响。仿真积灰密度从0逐步增加到5 g/m2，光伏组件输出功率仿真分析如图2所示。根据图2可知，随着光伏组件表面的积灰增加，光伏组件输出最大功率点数呈现明显的下降，与理论一致，下降幅度分别为3.43%、7.45%、11.77%、16.56%、21.17%。

图2 不同积灰密度下光伏组件P-V图

3 实验方案

首先，积灰密度需要在设备运转正常的条件下测出总的积灰量；其次，光线遇到积灰组件其作用降低，因此准确的透光率对于结果有重要影响；最后，得出总发电量。因为不同环境条件下灰尘的分布情况不同，所以选择的测量时间需要一定的普适性。

实验时间选取冬季（2018年12月）、春季（2019年3月）、夏季（2019年6月）、秋季（2019年9月）4个季节进行。如图3所示，实验在甘肃省某分布式光伏电站进行，该电站装机容量38 kW，光伏组件安装倾角为37°，采用两台逆变器将系统分为两个独立的分系统，经变压器升压后并入交流电网。

图3 分布式光伏电站现场图

如图4所示，为了方便测量积灰密度，选用和光伏组件表面玻璃材质相同的超白绒面钢化玻璃，编号为1#、2#、3#，将其放置在光伏组件表面，收集自然状态下积灰，每天测量2次（12点和16点）积灰量、光伏组件透光率并统计光伏电站当天发电量。积灰后光伏组件透光率ri的计算公式[14]为：

图4 积灰量测量样本布置图

式中，Eai是光伏组件玻璃表面照度，Ebi是清洁光伏组件玻璃背面照度；Eci是积灰光伏组件玻璃背面照度。

4 实验结果与分析

4.1 光伏组件积灰密度变化分析

实验中积灰质量由电子分析天平测量，积灰质量与积灰面积之比即为积灰密度。积灰密度随时间变化曲线如图5所示。

由图5可知，冬季（2018年12月）第2、5、21、27天为降雪天气，光伏组件表面积灰密度减小；春季（2019年3月）未出现雨雪天气，光伏组件表面积灰密度呈线性增加；夏季（2019年6月）降雨天气较多，其中第19—23天出现连续降雨天气，光伏组件表面积灰密度很小，约为0.001 g/m2；秋季（2019年9月）第8、9、11、12、16、18天出现降雨，积灰密度呈现减小的趋势，其中第8、9两天为连续降雨，积灰密度约为0.072 g/m2。分析实验结果可知，测试期间（自然积灰条件下），冬季积灰密度约为2.523 g/m2，平均每天增加0.081 g/m2；春季积灰密度约为5.309 g/m2，平均每天增加0.171 g/m2；夏季积灰密度约为0.264 g/m2，平均每天增加0.081 g/m2；秋季积灰密度约为1.886 g/m2，平均每天增加0.01 g/m2。

图5 积灰密度随时间变化曲线

4.2 光伏组件透光率变化分析

光伏组件透光率损失值变化曲线如图6所示。测试期间，冬季（2018年12月）透光率平均每天下降1.17%；春季（2019年3月）透光率平均每天下降1.49%；夏季（2019年6月）透光率平均每天下降0.14%；秋季（2019年9月）透光率平均每天下降0.74%。透光率变化趋势和积灰密度变化趋势基本相同。

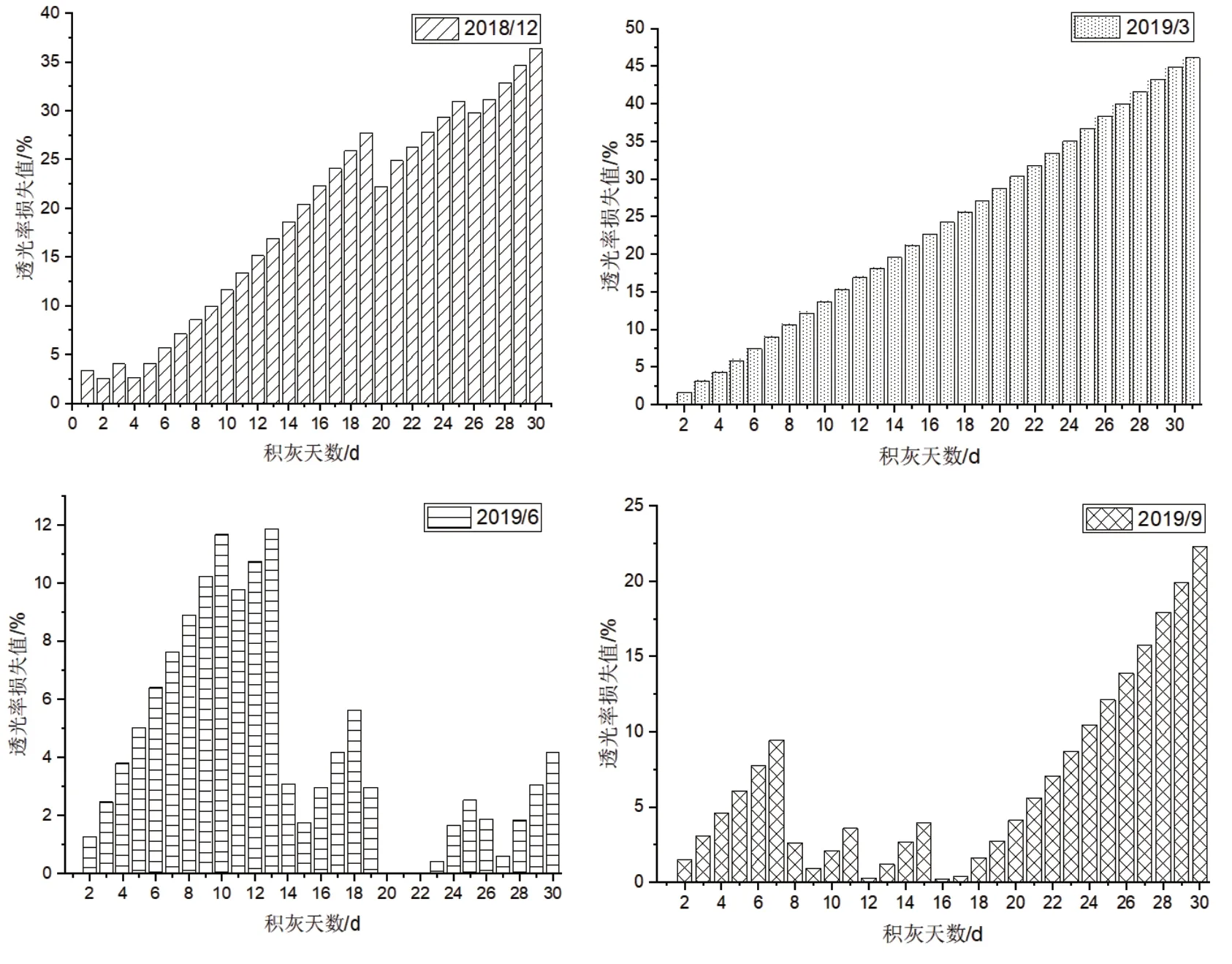
图6 光伏组件透光率损失值变化曲线

4.3 光伏组件发电量与积灰密度变化分析

光伏组件发电量与积灰密度变化如图7所示。由拟合曲线可以看出，在自然积灰条件下，由于降雨（雪）的影响只有少量点近似位于拟合曲线上，结合曲线变化规律和灰尘沉积理论，可将影响光伏组件输出电流的因素归结为积灰量和降水量。不同区域、不同季节，积灰量和降雨量存在较大差别，因此实验条件下运用拟合结果可以预测发电量变化情况，制定清理计划，提高经济效益。

图7 光伏组件发电量与积灰密度变化曲线

自然积灰条件下发电量与积灰时间近似呈二次函数的关系，其中2018年12月拟合公式为： y=131.25661 + 59.2867 x-23.9082 4x2，决 定 系数R2为0.03203。2019年3月拟合公式为：y=201.82535 + 14.66966x - 4.1050 3x2，决 定 系数R2为0.06672。2019年6月拟合公式为：y=194.54356 + 31.32289x - 96.1081 3x2，决 定 系数R2为0.02506。2019年9月拟合公式为：y=155.0036 2 - 164.7437 3x + 69.9675 2x2，决定系数R2为0.2313。

4.4 光伏电站清灰效益分析

实验所选用的光伏电站位于村道旁，故需定期对光伏组件表面进行清洗，以使经济效益最大化。光伏组件清洗采用最普遍的微水清洁方式，即通过高压水枪将光伏组件表面的积灰冲走。清洗周期随季节变化而不同，冬春季扬沙、浮尘天气较多，为了提高发电量，则需要适当增加清洗频率；夏秋季降雨天气较多（相对来说），可适当延长清洗周期。清洗前后光伏电站发电量测试曲线如图8所示。

由图8可知，在整个3月份内，观测1#与2#采集器，2#在前半月比1#低。在16号对其进行计划清理，2#超过1#的发电量。因此，由图8可知，在未清理条件下，1#比2#高，清理后两者结果相反，据此测算，清洗后光伏组件效率提高8.6%，平均每天可多发电7.98 kW·h。

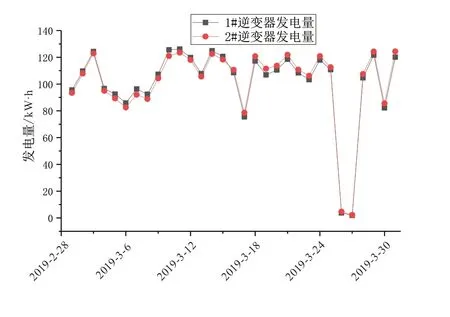
图8 某分布式光伏电站清洗前后发电量对比

结合仿真分析结果，在不考虑其他设备功率损失的情况下，当光伏组件积灰密度达到2 g/m2时，单体光伏组件的输出功率损失就高达7.45%，而实测数据显示在春季积灰15天的情况下，光伏电站发电量损失为8.6%，反推求得此时对应的光伏组件积灰密度为2.22 g/m2。计算积灰密度与实测积灰密度近似相等，故可推定该地春季最佳清灰周期为15天。同理可得，当地各个季节最佳清灰周期。

5 结论

本文以透光率和实验电流为研究对象，观测灰尘对发电量效率的影响。

1）在实验条件及环境相同时，观测时间越长，积灰密度越大。冬春季由于天气干燥，降水量较少，光伏组件表面积灰较严重，其中，春季平均积灰密度可达5.309 g/m2，透光率线性减少。随着自然环境变化如雨水冲刷，透光率会呈现波谷式变化。

2）制定清理计划，有益于电站的使用寿命。计算可得清洗后光伏组件效率提高8.6%，平均每天可多发电7.98 kW·h。

3）根据研究结果，结合西北地区降雨情况，初步确定某地光伏电站春季清灰周期为15天，夏、秋季可适当延长为1月1次。