基于组合赋权-VIKOR法的农机企业车间布局研究*
2022-06-08赵永满鲁浩男
闵 玉 ,赵永满 ,鲁浩男 ,周 雪
(石河子大学机械电气工程学院,新疆 石河子 832003)
农业生产季节性强,农机企业加工农业机械也随之具有季节性,企业加工机械的种类也随着季节的变化而不同,从而导致工厂车间布局不合理、堆放杂乱、生产效率低,企业也未能意识到车间设施布局的重要性。随着自动化、智能化和信息化的发展,农机企业开始逐步追求精益生产,而调研农机企业对车间设施布局的设计仅依赖于经验,缺乏科学的理论指导。合理的车间设施布局不仅可以减少物流成本,提升生产能力,还可以让企业形成质量意识,从追求规模扩张转变为追求结构改进。近年来,设施布局对企业的影响越来越大,许多学者都已投入有关理论与实践方面的研究,综合国内外大量研究发现设施布置的研究已经持续很长一段时间。1961年,Muther 提出系统规划布置设计(Systematic Layout Planning, SLP),作为车间设施布局规划的方法,其因条理清楚而得到较为广泛的应用[1]。在国内,石鑫提出将加权因素法与SLP相结合应用,对企业的生产设施进行规划,利用加权因素方法对布置方案评估打分,最后得出最终改善方案[2]。张惠、李成松、李玉林等提出了将SLP与系统仿真软件Flexsim相结合,更系统、更全面地解决微小型企业车间物流搬运的交叉迂回问题[3]。张梅等提出将熵权优化模型运用到评价方案的比选[4]。虽然大多数学者采用了较为复杂的评价模型,但是依旧采取专家打分法给指标赋权,无论是主观赋权还是客观赋权,都会影响最终各指标权重的计算结果。因此,课题组通过构建组合赋权模型,减少主观赋权的不确定性,利用VIKOR评价法对穴播器装配车间的布局方案进行评价,最终得到最优的装配车间布局方案。运用主客观相结合的组合赋权模型,优化传统的SLP,使SLP在方案比选中更科学合理,为后期车间设施布局方案比选提供理论指导。
1 农机企业车间布局规划方案评价指标体系
完善的车间设施布局规划方案评价指标体系,是得到最优车间布局的基础,是评估准确性和可靠性的重要保障。参考以往影响评估车间设施布局规划方案的因素[5-6],构建农机企业的车间布局规划方案评价指标体系,如图1所示。
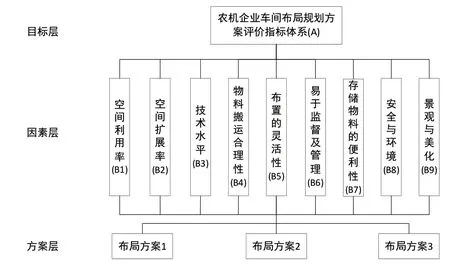
图1 农机企业车间布局规划方案评价指标体系
1)空间利用率(B1)。主要用来表示规划后的车间设施布局对于总装配车间的利用程度,常作为选择最优布局方案的主要因素之一。装配车间布置设计的空间利用率可用式(1)来衡量:

式中,U1表示车间的空间利用率;R表示车间的总面积;R1表示作业区的实际占地面积之和。
2)空间扩展率(B2)。用来表示车间设施规划设计的柔性程度,计算公式:

式中,U2表示车间的空间扩展率;Ti表示第i个作业区的实际占地面积;Si表示第i个作业区布置设计所占用的最小面积;其他含义同上。
3)技术水平(B3)。主要反映车间所用设备的先进性,通常用式(3)来表示:

式中,U3表示技术水平;C表示项目预期总收益;C1表示车间在机械化、自动化等方面的总投资。
4)物料搬运合理性(B4)。合理的物料搬运能够降低物料的搬运费用,减少加工时长,提高车间部件的运转效率。
5)布置的灵活性(B5)。灵活的设施布置不仅可以增加车间布局的柔性,提高装配速率,还可以降低企业对车间设备的投资成本。
6)易于监督及管理(B6)。合理的车间布局方案会更易于对设备及人员的监督与管理,提高产品的装配速率。
7)存储物料的便利性(B7)。若物料更好储存,可以降低物料的搬运距离,提高人员的工作效率。
8)安全与环境(B8)和景观与美化(B9)。车间的安全与周围的景观环境,不但影响企业的形象与发展,还对员工工作的态度有一定的影响。
2 组合赋权-VIKOR评价方法
2.1 层次分析法确定主观权重
层次分析法(AHP)主要是将人们的主观思维判断数学化,可以有效避免主观判断的随意性和偏好性。因此本文应用AHP来进行主观赋权。具体方法步骤[7]如下:
1)构建判断矩阵。根据评价指标体系,咨询相关有经验的专家,对于各指标的重要性进行判断,构造判断矩阵A。
2)层级中指标权重的计算。运用Matlab编写程序,计算出矩阵A的特征根与特征向量。
3)进行一致性检验。当CR<0.1时,认为矩阵 A 具有一致性。经过一致性检验后得到第i项指标的综合权重。
2.2 熵权法确定客观权重
熵权法是一种客观计算权重的方法,其本质就是利用计算得到的各指标信息熵的大小,判断各个指标的离散程度,即离散程度越大,该指标的影响越小;反之越大。具体方法步骤[8]如下。
对m个布局方案、n个评价指标的初始数据矩阵X = ( xij)n×m, i = 1,2,...,n; j = 1,2,...,m ,进行标准化处理,得到标准化后的矩阵 Y =( yij)n×m, i =1,2,...,n; j = 1,2,...,m 。
对于越大越优型指标:
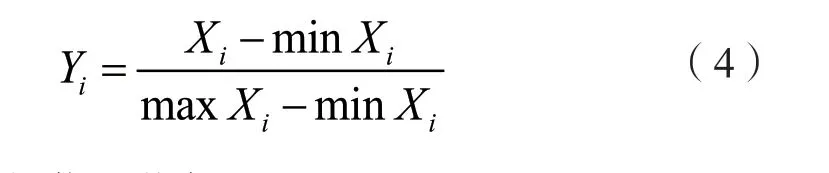
对于越小越优型指标:

其中,maxXi表示第j个布局方案中对应指标的最大值,minXi表示第j个布局方案中对应指标的最小值。
计算第j个评价对象下第i个指标的特征比重:

计算第i项指标的熵值:
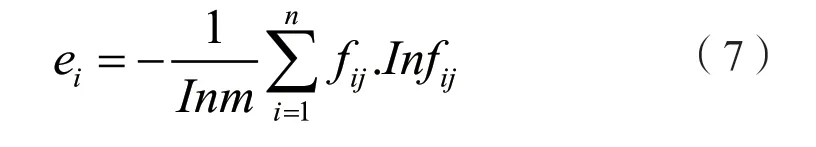
计算第i项指标的差异系数:

计算第i项指标的权重:

2.3 基于主客观赋权的综合赋权值
层次分析法受主观影响大,而熵权法需要有大量的样本数据支持,为了避免这两种计算权重的方法相互矛盾,采用乘法合成法计算组合权重,计算公式为:
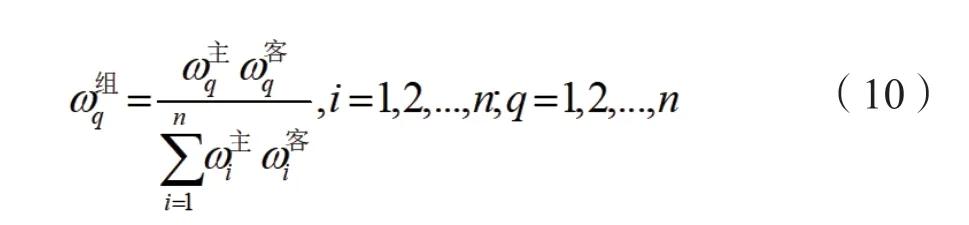
2.4 基于组合赋权的 VIKOR法车间布局方案评价模型
VIKOR法即折衷排序法,是一种逼近理想解的排序方法[9],其核心思想是在“群效用最大化”和“个体遗憾最小化”之间进行相互折衷,确定可折衷的最佳方案,远离最劣方案。与TOPSIS相比[10],VIKOR法可以得到折衷方案,具体方法步骤如下。
对初始数据矩阵 X = ( xij)n×m, i = 1,2,...,n; j = 1,2,...,m ,进行规范化处理,得到矩阵
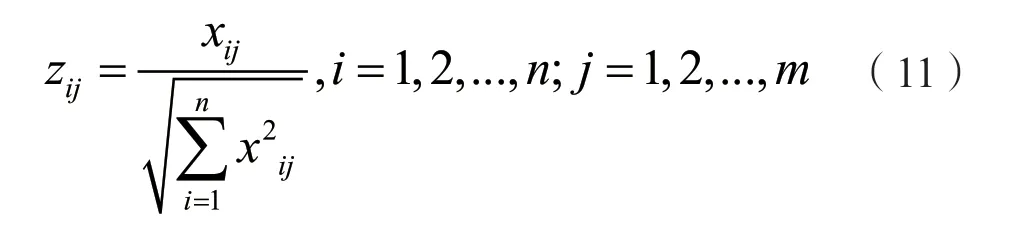
构成加权的规范化决策矩阵K,其中的元素:

分别计算正、负理想解D+、D-:
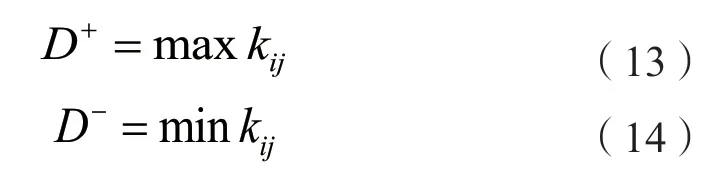
计算各方案的群体效益值Hj、个体遗憾值Pj和综合评价值Qj:

其中H+=maxHj,H-=minHj,P+=maxPj,P-=minPj,γ表示决策机制系数,一般地,取γ=0.5。根据Hj、Pj和Qj的值对被评价对象进行排序,满足的条件见文献[ 11],由此得出的Qj值越小,方案越优秀。
作出评价结果,按越小越优原则,将Hj、Pj和Qj值升序排列,评判方案优劣。若Qj值最小方案为 Y(1),n为方案数目。
条件1:优势可接受。
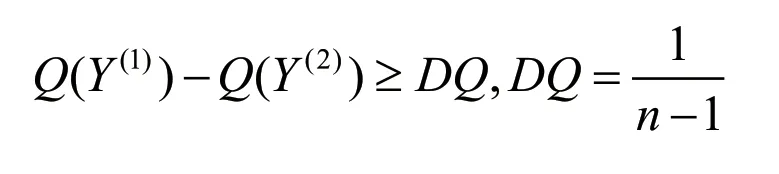
条件2:方案稳定性可接受。满足Qj值最小的方案,其Hj值和Pj值也应最小。如果上述两个条件均相符,则为最佳方案;若其中任何一个条件不满足,则需提出一个折衷方案集。
1)若条件1不符合,折衷方案集为Y(1),Y(2),…,Y(t),其中t的最大值由 Q(Y(1)) - Q(Y(2))≥ DQ 确定。
2)当只有条件2不符合时,则最优方案为排序第一和第二的方案,即折衷方案集包含Y(1)和Y(2)。
3 案例分析
3.1 某农机企业的穴播器装配车间原始资料收集
某农机企业是一家集研发、制造、销售为一体的农机化企业,生产播种机、秸秆粉碎机、残膜回收机等产品,该企业主要有3个车间,其中穴播器装配车间占地面积1900 m2,根据企业穴播器的装配生产过程,装配车间目前有11个作业单位,各作业单位详细如表1所示,其布局现状如图2所示。通过实地调研发现该车间在布局设计、工艺流程和车间内物流方面存在一些问题:1)装配车间空间利用不合理,配件存放区与腰带存放区在同一作业单位上,分为上下两层,增加员工劳动成本;2)装配车间布局较为杂乱,存在很多路线的交叉,增加搬运费用;3)钻床加工区和装配流水线离员工休息区较近,产生的噪声、振动等影响员工的休息,降低员工工作效率,且存在一定安全隐患。
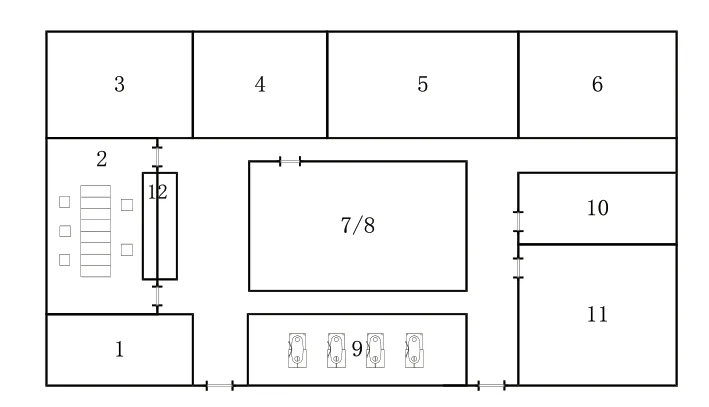
图2 某农机厂装配车间布局现状图
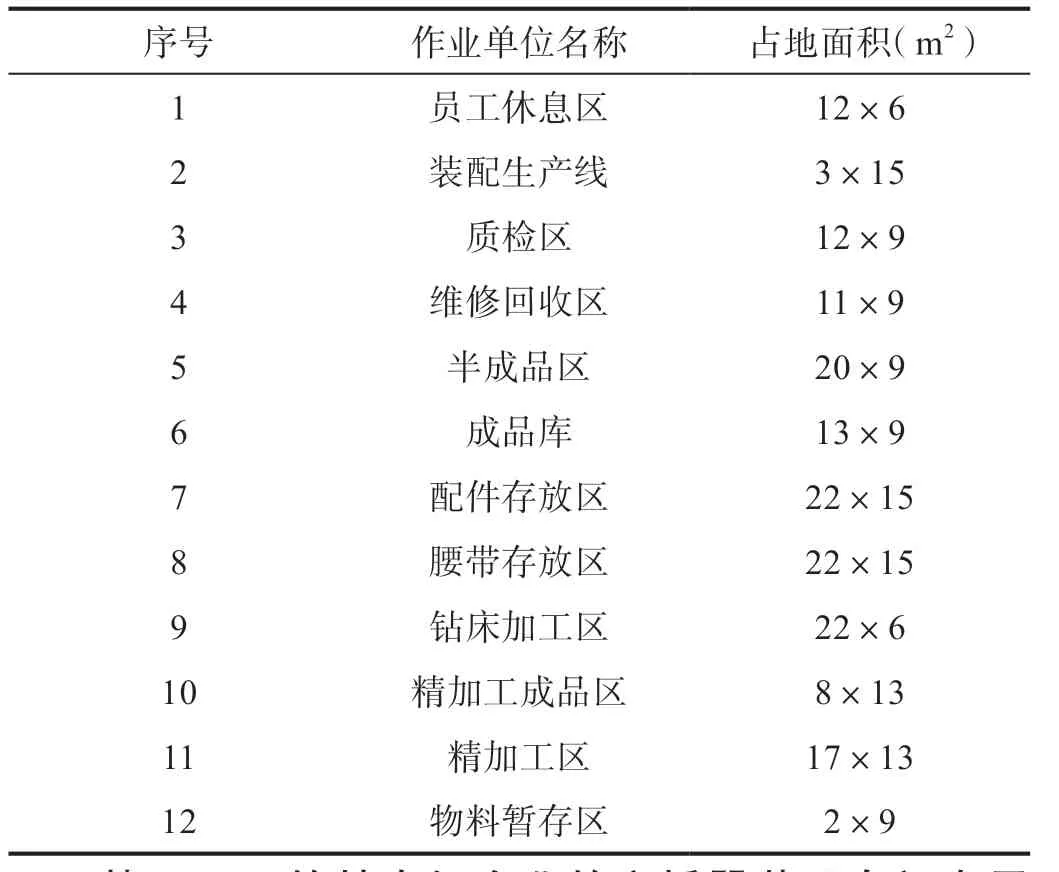
表1 作业单位汇总表
3.2 基于SLP的某农机企业的穴播器装配车间布局规划
经实地调研,某农机企业平均全年生产穴播器10000个左右,结合穴播器的装配流程图,得到各作业单位的物流强度汇总表如表2所示。根据“基准相互关系”[12-13],得到作业单位非物流关系表,由于作业单位5与12之间的物流关系等级与非物流等级关系矛盾,且计算结果与非物流关系也矛盾,因此表中最后调整为U级[14-15]。通过计算得到各作业单位综合接近程度排序表,根据作业单位的位置相关图,在已有各作业单位面积的基础上,考虑实际条件的限制,确定以下3个可行的布置方案供选择,如图3所示。
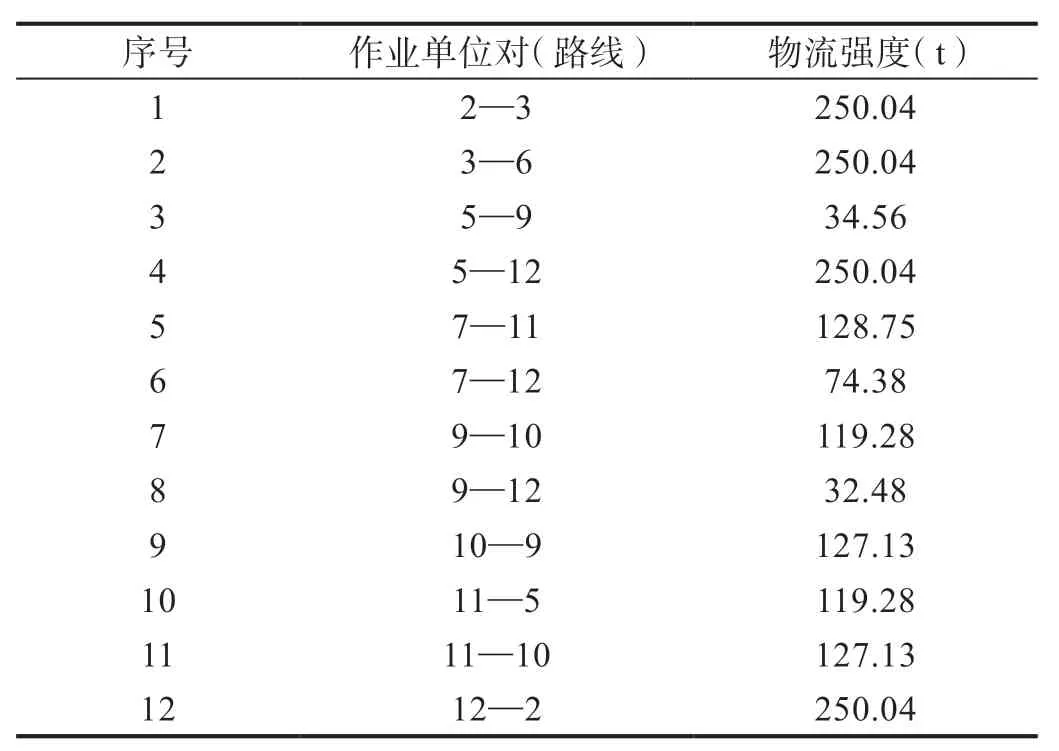
表2 物流强度汇总表
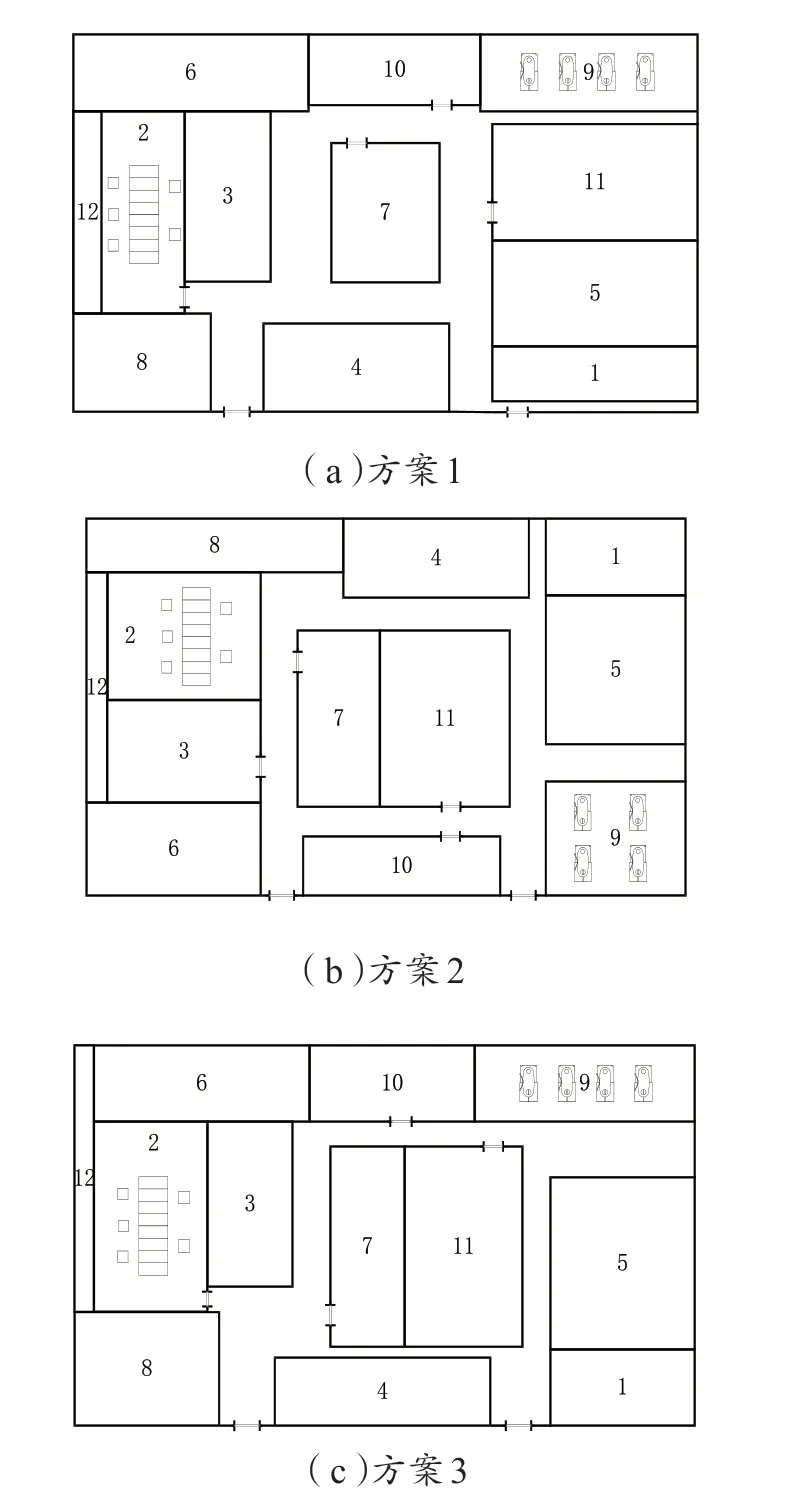
图3 某农机企业的穴播器装配车间布局优化方案
3.3 某农机企业的穴播器装配车间布局方案评价
采用式(4)和式(5)进行标准化处理,得到表3,层次分析法和熵权法分别计算各权重,并由式(10)计算综合权重,结果如表4所示。
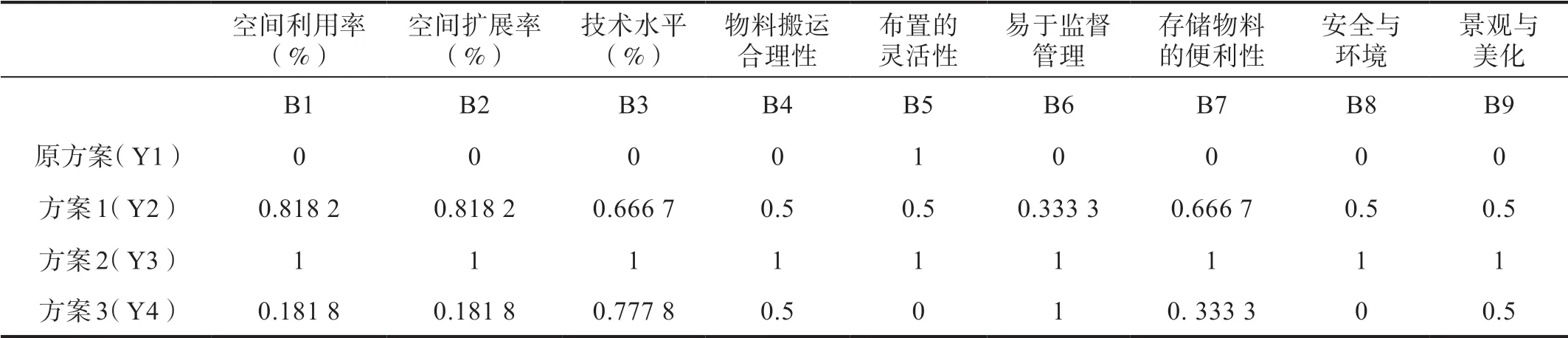
表3 指标数据标准化

表4 评价指标主客观赋权的综合权重
按照式(11)、式(12)得到加权的规范化决策矩阵,如表5所示。
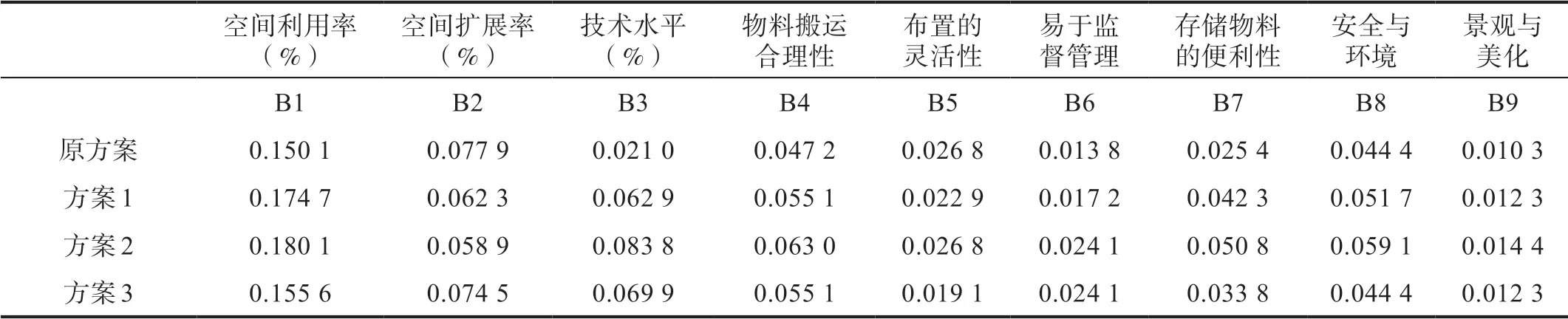
表5 加权后的规范化决策矩阵
根据式(13)、式(14)得到正、负理想解:D+=(0.1801,0.0779,0.0838,0.063,0.0268,0.0241,0.0508,0.0591,0.0144),D-=(0.1501,0.0589,0.021,0.0472,0.0191,0.0138,0.0254,0.0444,0.0103)。根据式(15)~(17)计算各方案的群体效益值Hj、个体遗憾值Pj和综合评价值Qj,如表6所示。

表6 各方案的Hj、Pj和Qj
由上表各评价对象的综合评价值Qj排序可以得到:方案2<方案1<方案3<原方案,由于VIKOR基本原理,评价结果需要满足上述条件1和条件2,经计算:DQ=1/(4-1)=1/3=0.3333,Q(Y2)-Q(Y3)=0.2019-0.0575=0.1444<0.3333,所以上述排序结果不能满足条件1,因此最终顺序方案为妥协折衷方案。
因为Q(Y1)-Q(Y3)=1-0.0575=0.9425>0.3333,Q(Y4)-Q(Y3)=0.6986-0.0575=0.6411>0.3333,且Y3(方案2)满足条件(2)中的Hj值和Pj值,且为四个方案里的最小值,因此可以得到第一名和第二名的排序结果是正确的,妥协集为(Y2,Y3)。根据上述计算结果,提议如下:1)将Y3设为最佳方案;2)如果条件允许,思量Y2为剩余方案;3)Y1为最差解。
4 结论
1)构建农机企业的车间设施布局规划方案评价指标体系,根据某农机企业的实际情况,添加有数据支撑的评价指标,减少主观赋权的随意性。
2)引入VIKOR法建立新的车间布局方案的评价模型。将层次分析法与熵权法计算的权重通过乘法合成法融合,形成主客观相结合的组合赋权模型,加入VIKOR评价方法,形成多指标决策的评价模型,为后期车间设施布局方案比选提供一定的参考。
3)优化传统的SLP,在方案评价步骤引入赋权评价模型,提高方案比选的科学合理性,减少农机企业车间在布局方案比选上的盲目性。
