基于小波神经网络-自适应反步控制的永磁同步电机无模型速度跟踪控制

郝 娜，詹志坤

(1.石家庄职业技术学院 电气与电子工程系，河北 石家庄 050081；2.燕山大学 工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有结构简单、功率因数高、转矩惯量比大和效率高等优点，已被广泛应用于机械制造、电动汽车等驱动领域。在实际应用中，一般采用双闭环比例积分控制作为其控制算法。只是PMSM驱动系统具有参数不确定性和逆变器非线性，可能给传统以固定增益的比例积分控制带来电流畸变、转矩脉动、稳态和动态性能下降等问题，甚至可能导致PMSM驱动系统的不稳定运行，因此传统比例积分控制不易在不确定性情形下保持良好的鲁棒性[1]。

随着现代控制理论的发展，各类先进的控制方法被逐渐应用于PMSM驱动系统。文献[2]在传统比例积分控制的基础上提出了模糊控制规则，提高了PMSM控制系统的速度跟踪控制性能和转矩输出的准确性。文献[3]提出了一种具有离散占空比优化的新型模型预测转矩控制方法,可有效减小转矩脉动、降低谐波电流。文献[4-5]基于模型预测控制技术，改进了PMSM电流和位置控制策略，提高了PMSM系统的鲁棒性。

Fliess于2014年提出了一种针对单输入单输出系统的无模型控制(Model-free Control，MFC)技术[6]，该技术使用超局部模型来近似表示整个非线性动态系统，并利用历史输入输出数据对未知非线性项进行估计。MFC技术控制参数少且与受控系统数学模型无关，对系统存在的内部外部扰动、测量噪声及未建模动态具有较强的鲁棒性[7-8]。从应用现状看，直流电机伺服系统[9-10]、机器人控制[11]、磁轴承[12]、气动系统[13]、无人驾驶[14]和医疗设备[15]等领域均有MFC技术成功应用的先例。

反步法是另一种应用较为广泛和有效的非线性控制设计算法，它将Lyapunov函数的选取与控制器的设计相结合，消除了经典无源性设计中相对阶为l的限制[16]，实现了系统稳定运行。但在PMSM机械角速度阶跃变化时初始速度跟踪误差较大，易造成转速超调量过大[17-18]。

针对上述问题，本文结合MFC和反步控制，提出一种基于小波神经网络-自适应反步无模型控制(Wavelet Neural Network based Model-free Adaptive Backstepping Control，WNN-MFABC)的PMSM速度控制方法。首先，建立d-q旋转坐标系下PMSM的一般数学模型，进一步构建针对表贴式PMSM(Surfaced-mounted PMSM,SMPMSM)的新型超局部模型，实现对系统中未知干扰和不确定性因素的实时模拟；其次，基于新型局部模型，采用反步法提出实现系统速度全局跟踪的控制算法，并结合小波神经网络和自适应技术设计新型局部模型非线性项的自适应参数估计律；最后，仿真验证了本文算法的有效性，仿真结果表明，本文算法改善了传统反推控制的稳态和动态性能，具有更强的鲁棒性。

1 永磁同步电机非参数模型

1.1 SMPMSM在参数摄动情况下的数学模型

在d-q旋转坐标系下，PMSM一般数学模型可表示为[19]

(1)

式中:Ld、Lq分别为定子绕组电感在d、q轴上的等效分量；id、iq分别为定子电流在d、q轴上的等效电流；Rs为定子绕组等效电阻；np为极对数；ud、uq分别为d、q轴上的定子电压；J为转动惯量；ω为转子角速度；B为粘滞摩擦系数；φf为转子永磁体产生的磁链；τL为负载转矩。

实际运行工况下，计及PMSM逆变器的非线性和外部扰动，同时考虑Ld=Lq=Ls，对于式(1)，可得d-q坐标系下SMPMSM的数学模型为

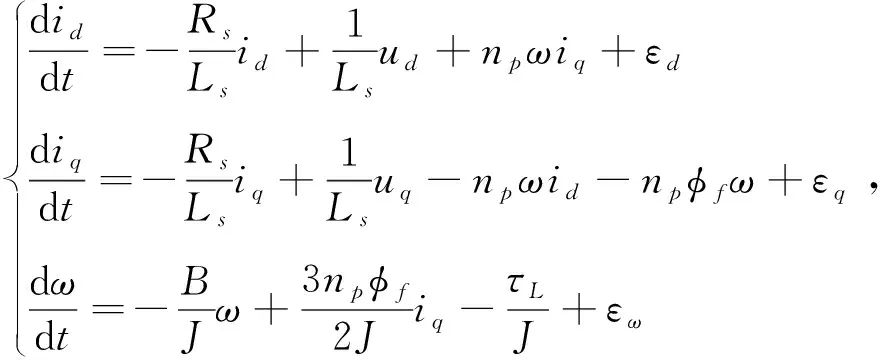
(2)

其中，

(3)

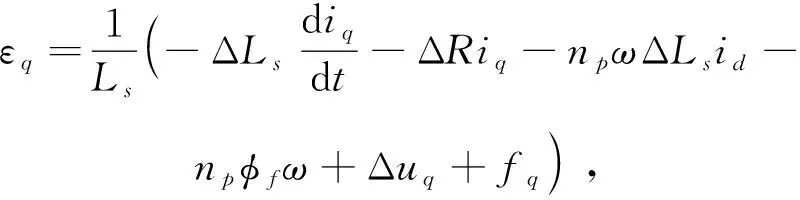
(4)

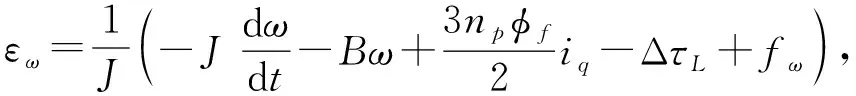
(5)

式中:εd、εq分别为定子在dq轴上电气参数不确定性扰动；εω为机械参数不确定性扰动；fd、fq、fω描述了实际运行工况中负载扰动的影响。

1.2 SMPMSM新型超局部模型

对于单输入单输出非线性系统，史涔溦等人利用非线性系统的输入和输出信号构建了超局部模型[20]，为了降低电流环对SMPMSM模型精度的依赖，提高控制器容错率，建立新型超局部模型：

(6)

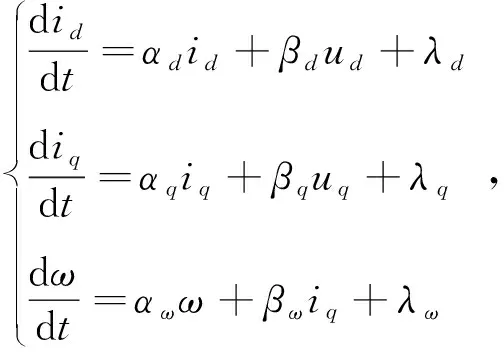
(7)

式中，λd、λq和λω为闭环干扰估计，由超局部模型不断更新。

对比SMPMSM数学模型式(2)和新型超局部模型式(7)，可以得到

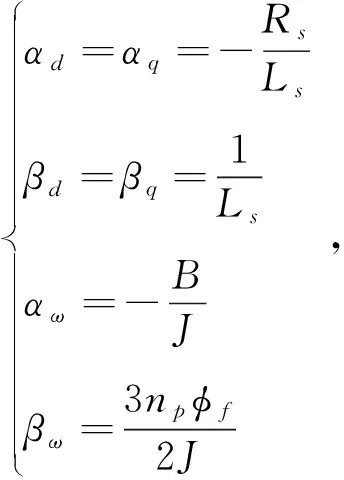
(8)

式中，αd、αq、αω、βd、βq和βω为预设常数，由于PMSM模型参数的不确定性，它们的实际值往往可能偏离预设值，但可通过调整λd、λq和λω来弥补其准确度，使得系统仍然保持良好的控制性能，因此无需知晓SMPMSM在实际中的准确参数，这就是新型超局部模型的优势所在。

2 小波神经网络-自适应反步无模型控制器设计

2.1 虚拟控制器设计

SMPMSM驱动系统的控制目标是为实现速度跟踪控制，将速度跟踪误差表示为[21]

e1=ω*-ω，

(9)

式中，ω*为转子参考机械角速度。

假定转子参考机械角速度ω*二次可微，将e1作为子系统的虚拟状态变量，对e1求导，同时结合式(7)，可得

(10)

为保证系统的稳定性，需让速度跟踪误差收敛于零。假定iq为虚拟控制量，子系统Lyapunov函数可以表示为[22]

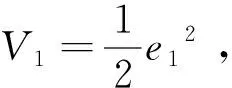
(11)

对式(11)求导得

(12)

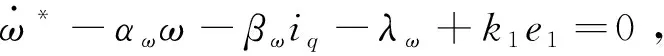
(13)

式中，k1为大于零的控制增益。

由式(13)，可求得虚拟控制量为

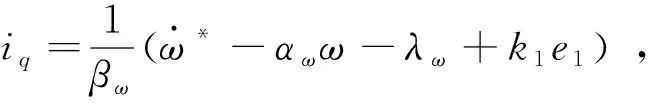
(14)

将式(14)带入式(12)，可得

(15)

因此满足Lyapunov函数的导数为半负定，可实现速度全局渐进跟踪控制，则取参考电流为

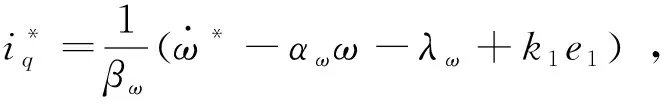
(16)

为了实现最大转矩，可令d轴定子参考电流为零，即

(17)

参考电流与dq轴定子电流状态值之间的误差为

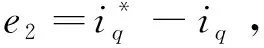
(18)

(19)

对式(18)求导，并结合式(16)，可得

(20)

对式(19)求导，并结合式(17)，可得

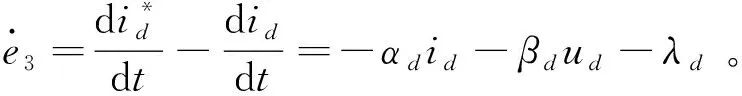
(21)

2.2 实际控制器设计和自适应参数估计

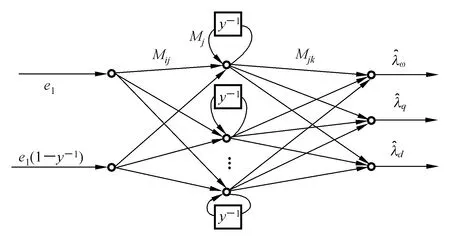
图1 小波神经网络结构Fig.1 Structure of wavelet neural network

选取e1、e2和e3构建第二个子系统，并选取Lyapunov函数

(22)

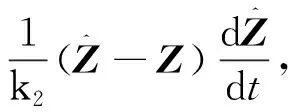
(23)

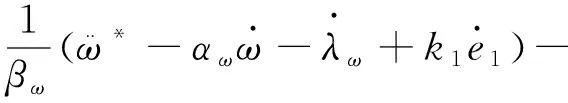
(24)

-αdid-βdud-λd=-k4e3，

(25)

式中，k3、k4为大于零的控制增益。

由式(24)和式(25)可得实际控制量

(26)

(27)

将式(26)、式(27)代入式(23)，可得

(28)

将自适应律设计为

(29)

基于WNN-MFABC的SMPMSM无模型速度跟踪控制驱动系统结构框图如图2所示。

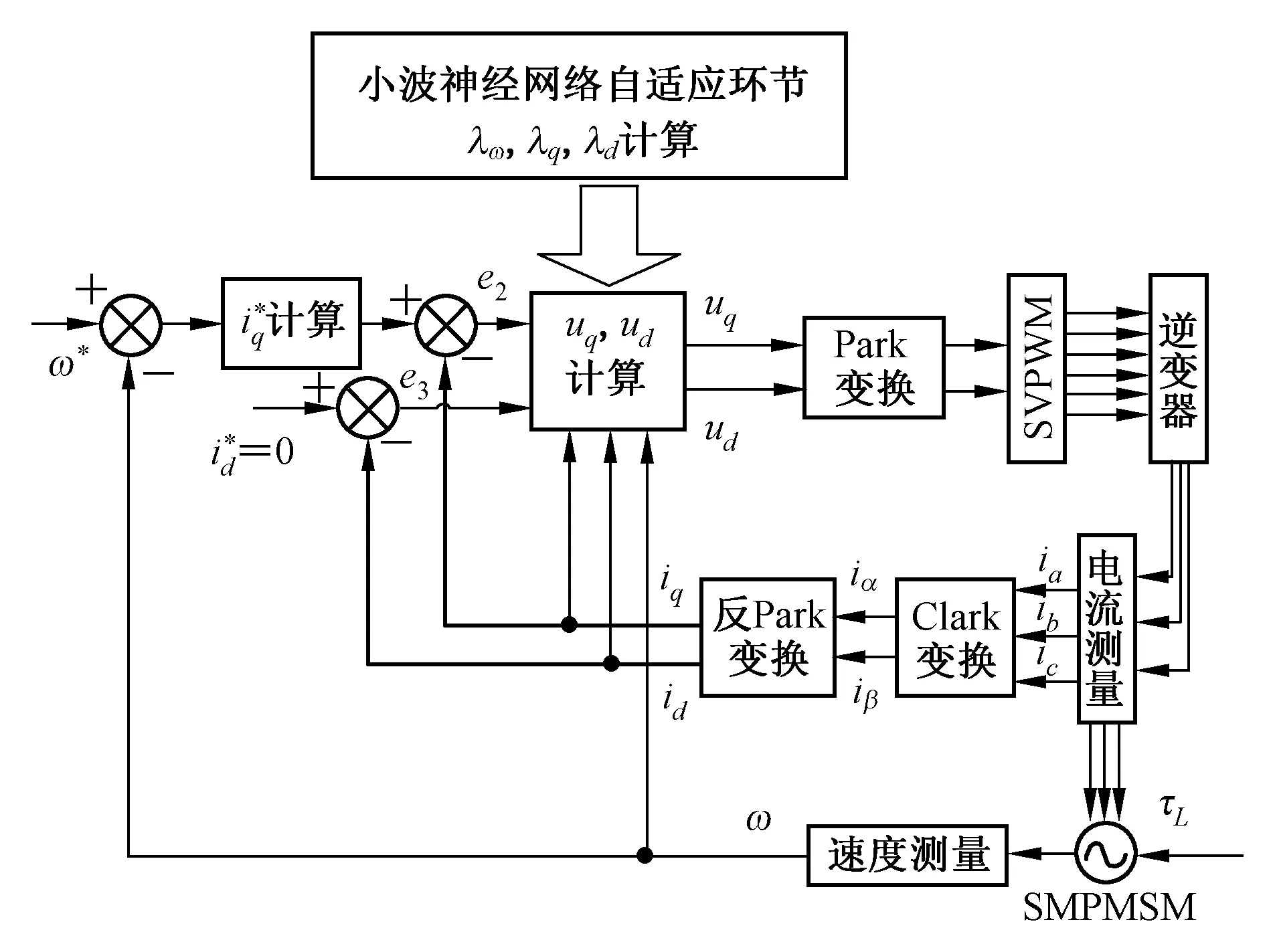
图2 驱动系统结构图Fig.2 Structure of driving system

3 稳定性分析

(30)

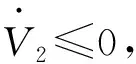
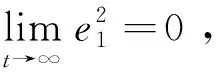
(31)

4 仿真分析

为了验证基于WNN-MFABC的SMPMSM无模型速度跟踪控制的性能，在MATLAB/Simulink环境下进行系统建模和仿真。SMPMSM的标称参数见表1。

表1 表贴式永磁同步电机的标称参数Tab.1 Nominal parameters of SMPMSM

采取试凑法选取控制参数为：k1=1.5、k2=100、k3=18.2和k4=7.3，小波神经网络隐含层神经元个数为6。设定负载转矩起始估计值为0.1 N·m，并设转子转速为50 rad/s，投入负载转矩观测器。在时间为0

图3(a)的速度跟踪控制结果表明，在负载扰动情况下，与传统反推控制相比，采用WNN-MFABC的无模型速度控制鲁棒性更强，负载扰动时转速变化相对较小，且能够迅速恢复至预设转速，具有较强的速度跟踪能力。图3(b)和图3(c)分别为SMPMSM的q轴和d轴电流控制效果，在负载扰动时，采用WNN-MFABC与传统反推控制相比稳态性能更优，电流波动更小，更能快恢复稳定。

5 结论

本文基于SMPMSM驱动系统的输入和输出数据，首先建立了考虑参数不确定性和未知扰动的转子角速度、d轴和q轴定子电流的新型超局部模型；然后，采用反步法设计系统实现系统速度全局跟踪控制，并利用三层递归小波神经网络对新型超局部模型非线性项进行逼近。仿真结果表明，与传统的反推控制相比，所提出的无模型小波神经网络-自适应反步控制可以估计并消除包括系统未建模部分和未知干扰在内的各种不确定性，且较传统反推控制相比提高了近一倍的响应速度和稳态恢复速度，表现出更快速的动态响应和更强的鲁棒性。