基于天气信息修正的短期冷热电负荷联合预测方法
2022-06-08曹晓波杨少华师锛博卢志刚
曹晓波,李 津,杨 鑫,杨少华,师锛博,卢志刚,*
(1.国网雄安新区供电公司,河北 雄安新区 071700;2.燕山大学 河北省电力电子节能与传动控制重点实验室,河北 秦皇岛 066004)
0 引言
能源互联网以大电网为基础平台,同时接入多种能源网络,这些网络互相联合和互相补充,由此达到满足用户冷热电负荷需求的目的,而冷热电负荷预测对能源互联网的稳定运行,对冷热电负荷的供求平衡都具有重要意义[1-4]。同时,冷热电负荷预测在冷热电联供系统的优化设计、运行调度和能量管理方面发挥着巨大的作用[5-6]。因此,提高冷热电负荷预测的准确性至关重要。
负荷预测是指根据已知的社会发展状况和系统需求状况,并且考虑自然条件、经济等相关因素,在满足一定精度要求的条件下,对未来负荷数据做出的估计和预测[7]。负荷预测主要是以电力负荷、冷需求负荷和热需求负荷为研究对象,其中电力负荷预测就是根据电力系统实时信息数据和历史数据,使用传统或者现代预测方法模型对未来电力系统负荷进行的预测。目前电力负荷预测的研究比较深入,已有大量研究成果。文献[8]提出了基于注意力机制的卷积神经网络(Convolutional Neural Network,CNN)和门控循环单元(Gated Recurrent Unit,GRU)神经网络的短期电力负荷预测方法,克服了深度学习中以循环神经网络(Recurrent Neural Network,RNN)为主体构建的预测模型难以有效提取历史序列中潜在高维特征且当时序过长时重要信息易丢失的缺点,提高了预测精度及稳定性。文献[9]在长短期记忆(Long Short-Term Memory,LSTM)网络模型和宽度&深度(Wide&Deep)模型的基础上提出基于Wide&Deep-LSTM的深度学习短期负荷预测模型,该模型不仅具有深度神经网络的学习能力,而且发挥了LSTM模块的时间序列信息表达特性,从而解决了台区电力负荷预测的多特征维度及时序性特征问题,进一步提高了预测精度。文献[10]提出一种基于差分分解(Differential Decomposition,DD)和误差补偿(Error Compensation,EC)的GRU神经网络短期电力负荷预测方法(DD-EC-GRU),解决了基于序列分解方法出现的误差积累的问题,并克服了现有方法忽略历史预测误差与当前预测结果存在相关关系的缺点,提高了预测精度。冷负荷预测和热负荷预测是综合能源系统运行的重要一环,它们会受到季节变化和气象变化的影响,更与用户用能数据密切相关。文献[11]构建了一种基于粒子群优化算法(Particle Swarm Optimization,PSO)的反向传播(Back Propagation,BP)神经网络模型(PSO-BP)并进行室内冷负荷短期预测,该方法结合了PSO具有较强的全局搜索能力和快速的收敛速度的特点,使得整个模型的预测精度和收敛速度都得到较大的提高。文献[12]建立了小波-BP网络预测模型,并将其应用到冰蓄冷空调负荷预测中,该方法通过结合小波多分辨分析与神经网络自学习自适应能力强的优点,使得预测精度具有良好的效果。文献[13]提出了一种基于遗传算法优化BP神经网络的短期热负荷预测方法,该方法结合了遗传算法(Genetic Algorithm,GA)与BP神经网络,利用遗传算法的全局搜索能力,补足了BP神经网络的缺点,提高了热负荷预测精度。文献[14]结合PSO和最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM) 提出了基于交叉验证意义下的 PSO-LSSVM 热负荷预测模型,实现了对换热站负荷的高精度预测。
在上述研究中,大部分都是只对单一的负荷进行预测,没有考虑不同种类负荷之间内部的关联性以及各种负荷的规律性、季节性,从而导致不同种类负荷单独预测的精度不高,而冷热电负荷联合预测是使用一个预测模型同时对冷热电三种负荷进行预测。同时,随着深度学习的发展,现有的负荷预测中使用的预测模型大部分为深度学习模型,由于其层数、超参数较多,导致模型使用较为复杂[15-16]。针对上述问题,本文提出了一种基于天气信息修正的短期冷热电负荷预测框架以及基于增量学习的宽度学习(Incremental Learning Broad Learning System,ILBLS)预测模型。首先使用基于增量学习的宽度学习对气象局提供的天气信息进行修正,以此来降低其对冷热电负荷预测的影响。其次,使用X-12-ARMIA对冷热电三种负荷进行季节性分解。最后,使用基于增量学习的宽度学习预测模型对分解后的分量进行预测,从而得到最终的预测结果。
1 预测模型
宽度学习系统 (Broad Learning System,BLS)[17-19]是一种基于随机向量函数链接神经网络和单层前馈神经网络的单层增量式神经网络,其基本原理是:首先通过一系列随机映射将原始输入数据变为特征节点矩阵;然后再经过一系列的随机增强变换,在上一步特征节点矩阵的基础上,形成增强节点矩阵;最后将所有的特征节点矩阵和增强节点矩阵送入输出端,并借助伪逆求出隐层与输出层之间的连接权重。
相比于传统的深层网络模型,这个模型在保证一定精度的同时,具有快速、简洁的特点[20],这是因为在特征节点矩阵和增强节点矩阵的生成过程中,BLS所有的隐层连接权没有变化并且都是随机产生,故而只需要求出隐层与输出层之间的连接权。另外,当BLS直接训练后可能无法达到理想的性能时,BLS可使用自己的增量学习范式达到快速实现模型重建的目的。
1.1 宽度学习
BLS的基本结构示意图如图1所示,其隐藏层包括两部分,分别为特征节点和增强节点。Z1,Z2,…,Zn为特征节点矩阵,H1,H2,…,Hm为增强节点矩阵,Wm为隐层和输出层之间的连接权矩阵。
首先,输入矩阵X经过n组特征映射形成特征节点矩阵Z1,Z2,…,Zn:
Zi=φi(XWei+βei),
(1)
其中,i=1,2,…,n,φi为线性或非线性激活函数,通常默认为一个线性变换,Wei和βei分别为随机权重矩阵和随机偏置矩阵。Wei和βei经常通过稀疏自编码器进行微调,这是为了得到输入特征的稀疏表示。将n组特征节点矩阵拼接成一个整体,得到总的特征节点矩阵:
Zn=[Z1,Z2,…,Zn],
(2)
然后经过m组增强变换,形成增强节点矩阵H1,H2,…,Hm:
Hj=ξj(ZnWhj+βhj),
(3)
其中,j=1,2,…,m,ξj为一个非线性激活函数,一般可将其设置为双曲正切函数:
ξj(x)=tanh(x),
(4)
Whj和βhj也为随机权重矩阵和随机偏置矩阵。将m组增强节点拼接为
Hm=[H1,H2,…,Hm]。
(5)

图1 BLS的结构示意图Fig.1 Schematic diagram of BLS structure
为了方便起见,这里引入新的变量,记为
A=[Zn|Hm],
(6)
则系统的输出为

(7)


(8)

Wm=(ATA+λI)-1ATY,
(9)
其中,AT为A的转置矩阵,I为单位矩阵。当λ→0时,设:

(10)
则可得
Wm=A+Y,
(11)
其中,A+表示为A的伪逆。
1.2 基于增量学习的宽度学习
目前,大多研究使用基础的BLS。文献[21]结合自组织映射和BLS对光伏发电功率进行超短期预测,其在使用自组织映射对各时刻的光伏数据进行精细化聚类的基础上,通过BLS训练神经网络,提高了计算效率。文献[22]针对BLS参数选择的问题,将网格搜索法与BLS进行结合,提出一种BLS 的特征自适应提取方法。但是,对于一些情况,BLS直接训练后可能无法达到理想的性能[23],为此提出了基于增量学习的宽度学习。增量学习的核心思想就是,在已经得出的计算结果和新数据的基础之上进行更新,从而只需少量计算就能得到更新的权重。相比深度学习在反复训练过程中时常陷入局部最优无法自拔,增量学习的优势非常明显。
若模型结构需要收集到新的训练数据或扩展宽度,BLS不需要模型的重新训练过程,只需要一些高效的增量计算来动态更新系统,比如BLS增强节点增量学习[24]。在某些特殊状况下,插入额外的增强节点会让系统拥有更好更优秀的性能。如图2所示,在保持特征节点不变的情况下新增增强节点,则系统的隐藏层变为:
Am+1=[A|ξ(ZnWm+1+βm+1)],
(12)
其中,ξ为激活函数,Wm+1和βm+1为新的随机权重矩阵和随机偏置矩阵,则可得到
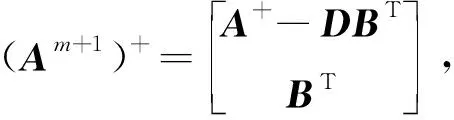
(13)
其中,D=A+ξ(ZnWm+1+βm+1)。

(14)
其中,C=ξ(ZnWm+1+βm+1)-AD,C+为C的伪逆。新的权重则为

(15)
通过以上计算过程可以得出,添加新的增强节点后,我们只需要对一个较小的矩阵计算伪逆,从而极大地降低了计算量。
1.3 预测结果评价指标
本文采用均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)以及平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)作为预测评价指标。
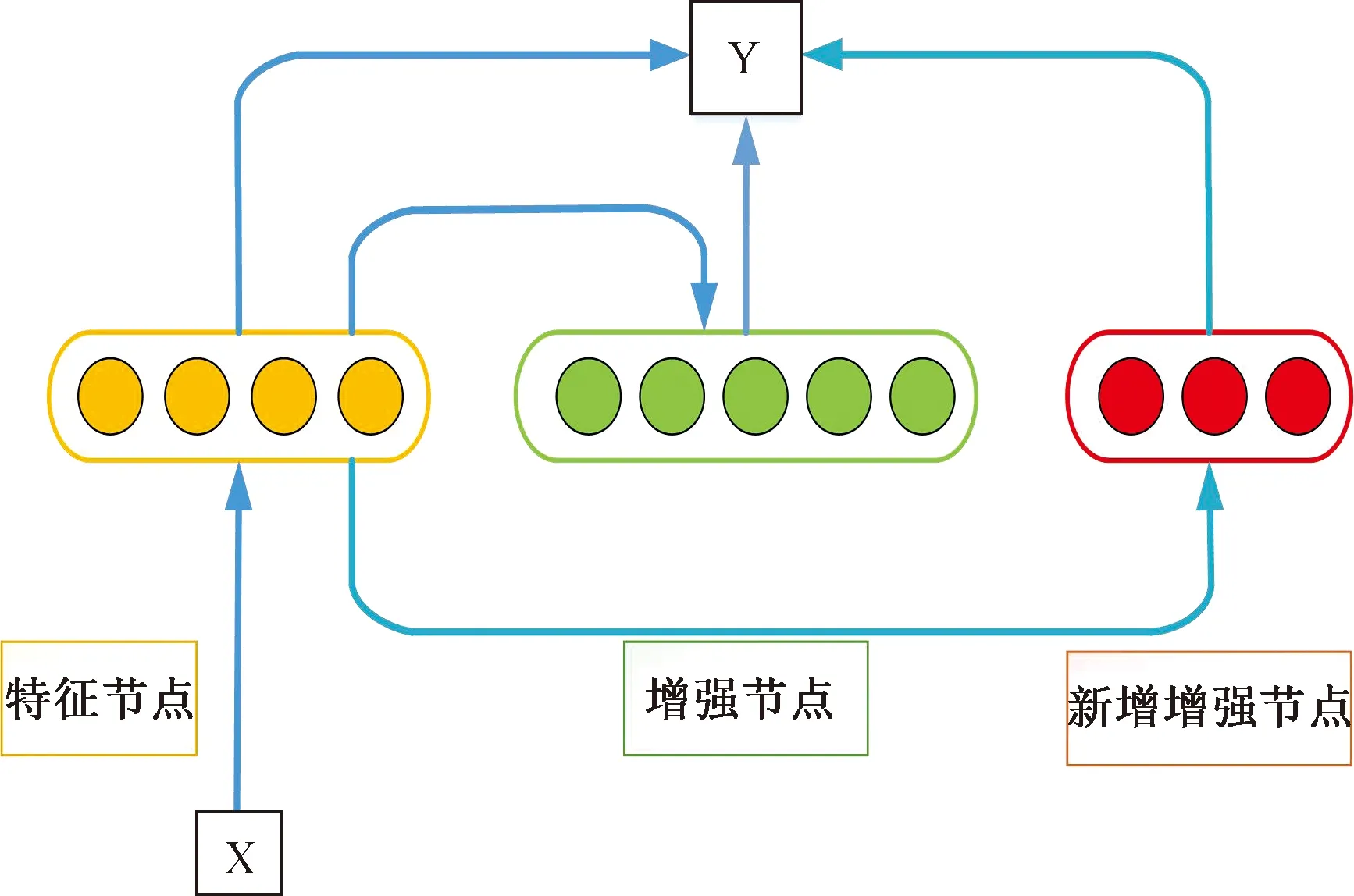
图2 BLS增强节点增量学习示意图Fig.2 Schematic diagram of BLS enhanced node incremental learning
假设数据真实值为
y={y1,y2,…,yn},
(16)
数据预测值为
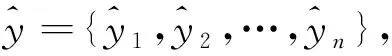
(17)
对于均方根误差,其计算公式为

(18)
其计算结果的范围为[0,+∞)。RMSE在数量级上比较直观,当RMSE=0时,预测值与真实值完美重合,这时模型预测的效果最好,即为完美模型;当RMSE≠0时,比如RMSE=10,这时可以认为回归效果比真实值平均相差10。总之RMSE的值越小,预测的误差就越小,模型也越优秀,模型精确度也越高。
对于平均绝对误差,其计算方法如下:

(19)
平均绝对误差可以排除误差相互抵消的问题,能够准确地反映预测误差的大小,MAE计算结果的范围也是[0,+∞),其值为0时模型的预测效果最好。
对于平均绝对百分比误差,它是一个百分比值,故其比其他统计量更容易理解,也更加直观,其计算公式如下:

(20)
平均绝对百分比误差的范围是[0,+∞),当模型为完美模型时,MAPE=0%;当MAPE>100%时,模型预测效果很差,认为模型为劣质模型。
2 预测框架
冷热电负荷一般与天气信息具有一定的相关性并且具有明显的周期性。相关性主要表现在冷热负荷受温度影响比较大,温度较高时冷负荷用能较高,而温度较低时热负荷用能较大;冷热电三种负荷都具有明显的周期性,电负荷中占比较高的一般为工业负荷,部分工业负荷主要集中在白天进行工业生产,还有一部分能耗较大的工业负荷选择在夜间电价较低时进行工业生产;冷负荷在白天能耗较高,在中午或者下午由于温度的上升从而达到顶峰;热负荷一般在晚上由于温度的降低达到最高,在中午或者下午由于温度的升高而降低。因此,天气信息预测的准确性将直接影响冷热电负荷预测的准确性。
2.1 天气信息修正
现有的天气信息的获取来源主要是中国气象局对气象信息的预测,然而气象部门提供的天气信息数据存在较为明显的误差,直接将其输入预测模型会使预测结果存在明显的误差。
基于上述问题,本文提出一种基于天气信息修正的短期冷热电负荷预测模型。首先对气象历史数据进行采集,采集的历史数据包括真实的天气数据Tt,气象局预测的天气数据Tp。将过去的历史真实数据、历史预测数据以及未来的预测数据结合起来,得到误差较小的天气预测数据,从而提高预测精度。天气信息修正流程图如图3所示。

图3 天气信息修正流程图Fig.3 Flow chart of weather information correction
使用历史预测天气数据Tp作为模型的输入,历史真实天气数据Tt作为模型的输出,对基于增量学习的宽度学习进行训练,训练目标如下:
Tt=f(Tp),
(21)
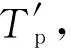
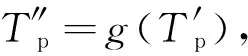
(22)
其中,g(t)为经过训练的模型。
2.2 冷热电负荷预测框架
针对冷热电负荷明显的季节性以及周期性,本文利用X-12-自回归积分滑动平均(X-12-ARIMA)季节分解[25],提出了一种基于X-12-ARIMA和ILBLS的预测模型:X-12-ARIMA-ILBLS模型。首先,将冷热电负荷冷热电三种负荷分解成趋势及循环分量、季节分量、不规则分量三部分。然后使用ILBLS预测模型对三种分量进行预测,进而得到最终的预测结果,预测流程图如图4所示。
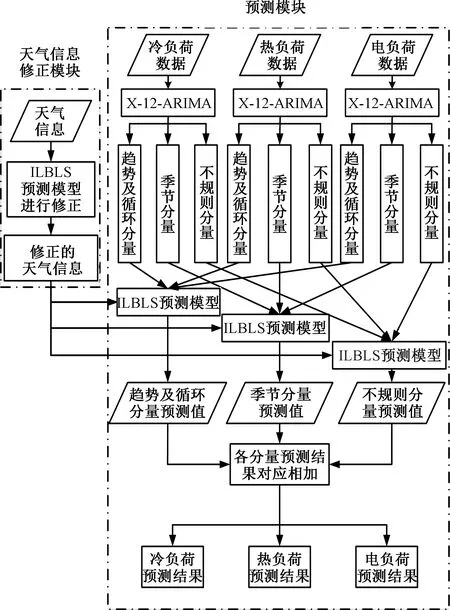
图4 预测流程图Fig.4 Forecast flow chart
3 算例分析
为了验证本文提出的天气信息修正方法以及预测模型的准确性,本文选取了中国北部地区某城市2017年7月18日-2017年7月31日共14天的冷热电的负荷数据、地区真实气象数据以及气象局天气信息预测数据,数据集采集的频率为每小时采集一次,共采集336组数据,选取前312组数据作为训练集,对最后24时刻的冷热电负荷以及气象数据进行预测。本文模型构建及训练在基于Python 3.6以及tensorflow 2.4架构的Pycharm3.3公开版上进行,硬件平台采用Intel Core i7 CPU以及NVIDIA GTX 1650 GPU。
本文的仿真算例分为四个部分。第一,使用本文所使用的ILBLS模型对待预测日气象局天气预测信息进行修正,减小气象局天气信息预测误差,使之更加接近真实天气数据;第二,使用X-12-ARIMA分别对冷热电三种负荷进行分解;第三,使用气象局提供的气象信息进行冷热电负荷预测;第四,使用修正后的天气预测信息作为模型的输入对冷热电负荷进行预测。具体分析如下:
1) 天气预测信息修正
本部分使用2017年7月8日-2017年7月31日气象局天气信息预测数据以及历史真实天气信息数据,采集频率为每小时一次。以温度为例,使用ILBLS对气象局气象预测温度进行修正,修正结果如图5所示,结果误差分析如表1所示。

图5 天气信息修正结果Fig.5 Weather information correction result
如表1所示,相比于气象局气象预测温度与真实温度之间的误差,修正温度与真实温度之间的误差明显减少,以MAPE为例,修正之后比修正之前减小了2.05%,修正之后的温度数据更加接近真实温度数据。

表1 天气信息修正前后误差对比Tab.1 Error comparison before and after weather information correction
2) 季节分解
对冷热电负荷数据进行季节分解,分别得到每种负荷的3个分量:长期趋势及循环分量,季节分量以及不规则分量。以电负荷序列为例,季节分解结果如图6所示。

图6 季节分解结果Fig.6 Seasonal decomposition results
3) 使用气象局天气预测信息的预测结果
本部分预测使用气象局天气信息预测数据作为输入,分别使用BP神经网络、LSTM、 BLS、ILBLS以及X-12-ARIMA-ILBLS五种模型对所选择地区2017年7月31日24时刻的冷热电负荷数据进行预测。预测结果如图7~9所示,结果误差分析如表2~4所示。为了区分不同种类负荷之间的预测结果,本文所有的冷、热、电负荷预测结果均分开显示。
通过对预测结果进行分析并计算误差,以热负荷的MAPE为例,本文所提X-12-ARIMA-ILBLS预测模型为3.30%,比BP神经网络减少5.82%,比LSTM减少4.37%,比BLS减少2.1%,比ILBLS减少1.31%。冷负荷与电负荷预测结果误差与热负荷几乎相同。通过不同模型之间预测结果对比,本文所提X-12-ARIMA-ILBLS预测模型的预测精度最优,误差最小。

图7 电负荷预测结果对比Fig.7 Comparison of power load forecast results

图8 冷负荷预测结果对比Fig.8 Comparison of cooling load forecast results

图9 热负荷预测结果对比Fig.9 Comparison of heating load forecast results
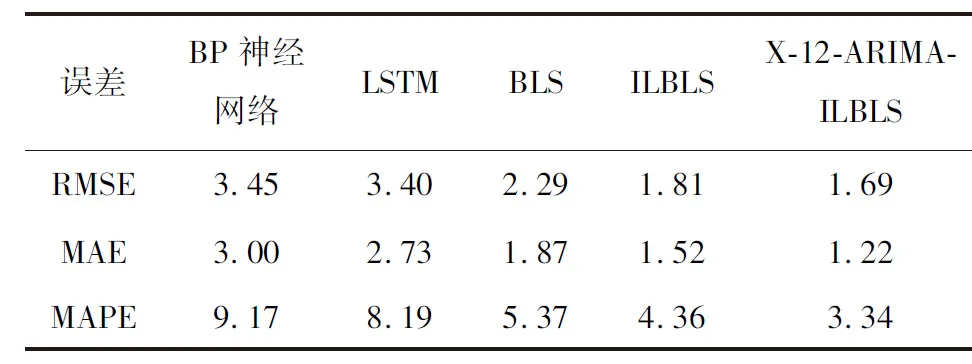
表2 电负荷预测误差对比Tab.2 Error comparison of power load forecast

表3 冷负荷预测误差对比Tab.3 Error comparison of cooling load forecast

表4 热负荷预测误差对比Tab.4 Error comparison of heating load forecast
4)使用不同温度数据及最优模型的预测结果
本部分预测使用X-12-ARIMA-ILBLS预测模型,并将修正的天气信息数据作为模型的输入,以此来对所选择地区2017年7月31日24时刻的冷热电负荷进行预测。本部分预测所使用的数据集以及数据集的划分均与3)部分相同,预测结果如图10~12所示,预测误差分析如表5~7所示。

表5 天气信息修正前后的电负荷预测误差分析Tab.5 Error analysis of electric load forecast before and after weather Information correction
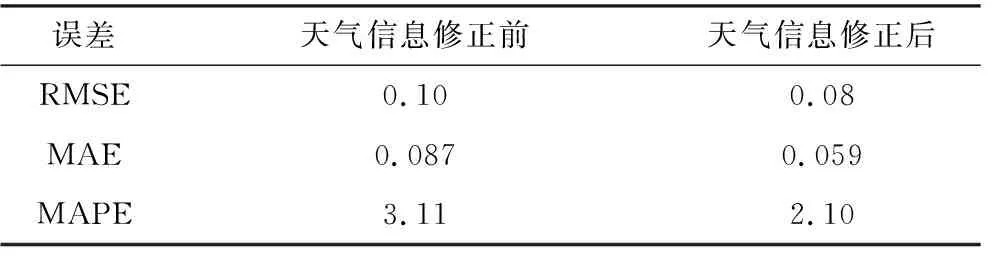
表6 天气信息修正前后的冷负荷预测误差分析Tab.6 Error analysis of cooling load forecast before and after weather Information correction

表7 天气信息修正前后的热负荷预测误差分析Tab.7 Error analysis of heat load forecast before and after weather information correction

图10 天气信息修正前后的电负荷预测结果对比Fig.10 Comparison of power load forecast results before and after weather information correction
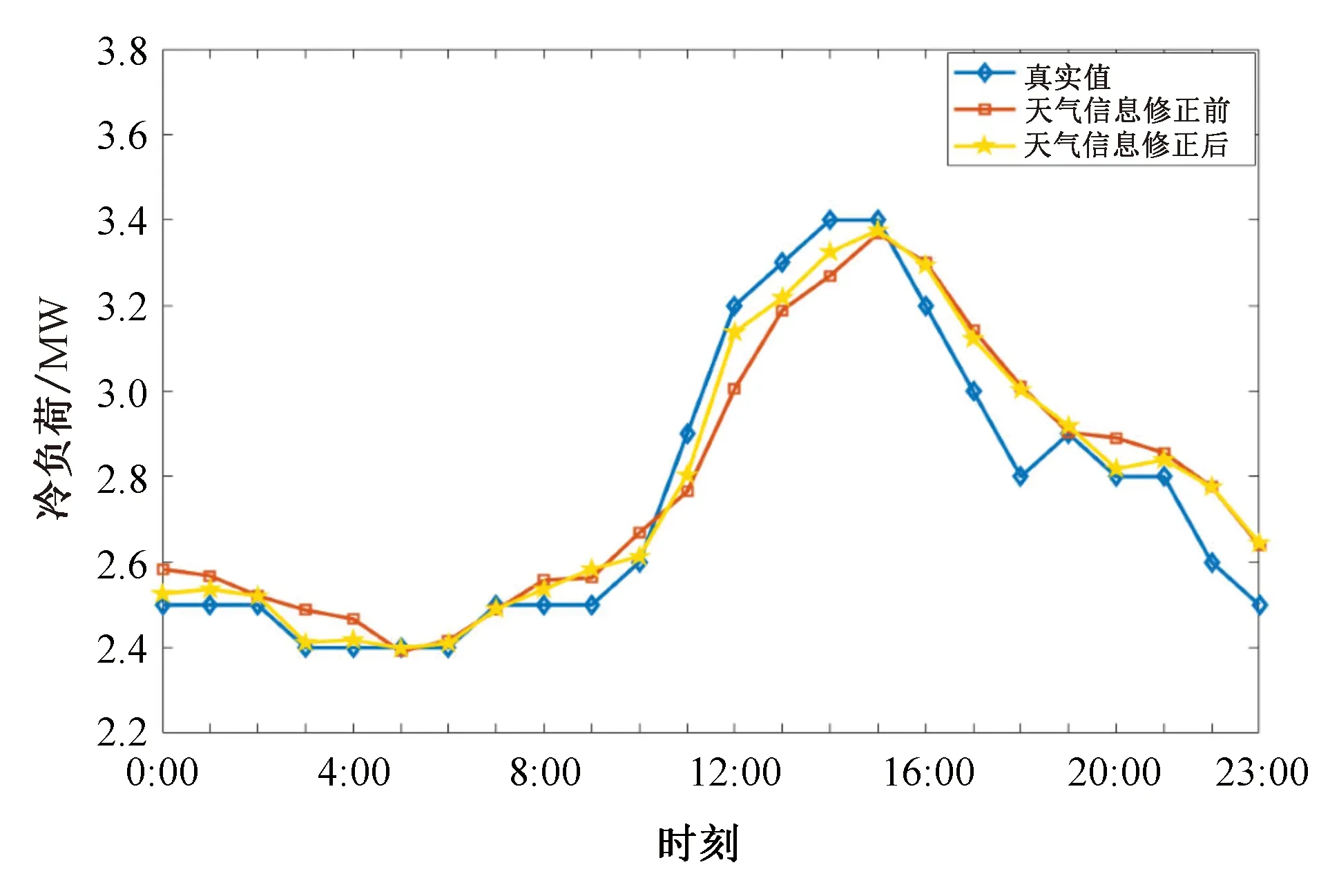
图11 天气信息修正前后的冷负荷预测结果对比Fig.11 Comparison of cooling load forecast results before and after weather information correction

图12 天气信息修正前后的热负荷预测结果对比Fig.12 Comparison of heating load forecast results before and after weather information correction
根据预测结果,使用天气修正方法后,预测精度更高,预测效果更优,以电负荷的MAPE为例,预测误差比使用修正方法之前减少1.14%。冷热电负荷的预测误差均有明显减少,证明了天气信息修正方法可以有效提高预测的精度。
4 结论
本文考虑气象局天气信息数据对冷热电负荷预测造成误差,并结合X-12-ARIMA和ILBLS,提出了一种基于天气信息修正的短期冷热电负荷预测框架,从而提高了冷热电联合预测的精度。最后使用中国北方某城市的冷热电负荷数据作为算例进行验证,最终得到如下结论:
1) 本文使用的基于增量学习的宽度学习预测模型相较于基础的宽度学习模型、长短期记忆神经网络以及BP神经网络能够有效提高预测精度。
2) 相较于使用未修正天气预测信息的预测模型,本文提出的基于天气信息修正的预测框架能够提高模型的预测精度。
3) 冷热电负荷存在明显的季节性以及周期性,对其进行季节性分解可以有效提高预测精度。
