基于GA-FELM算法的冷轧轧制力预测模型
2022-06-08陈树宗白芸松侯佳琦华长春
陈树宗,白芸松,侯佳琦,华长春
(燕山大学 电气工程学院,河北 秦皇岛 066004)
0 引言
在冷轧生产过程中,轧制力模型在模型系统中处于核心地位,它是辊缝设定值计算、轧制负荷分配、AGC增益系数计算及板形控制设定的基础。冷轧轧制过程具有多工况、深度非线性、强耦合性和不确定性等特点,存在润滑状态、带钢头尾力学性能、设备工况等多种难以表征的变化。例如,在轧机加减速过程中,轧制速度可从过焊缝时的100~250 m/min升速至稳速轧制时的1 000 m/min以上,轧制润滑状态在边界润滑、混合润滑和液体润滑之间切换,润滑状态随着轧制液黏度、轧制速度和轧制力载荷变化;轧制润滑状态的变化导致油膜厚度随之改变,从而造成各个机架的轧辊与带材之间的摩擦状态也不断地发生着变化。因此,传统的轧制力模型并不能对轧制过程进行完全精确的描述,同时模型在推导过程中作了大量假设,设定值和实际值之间往往存在差异,所以一些学者尝试从理论模型进行改进,从而提高轧制力模型在特定生产环境下的预测精度。如,徐利璞等[1]通过对某1880精轧机组F3机架的轧制过程的模拟和分析,应用ANSYS/LS-DYNA软件建立了PC轧机轧制力有限元模型;刘宝龙等[2]运用平面应变主应力法的同时采用了引入修正系数且考虑剪切力的屈服方程,建立了板材异步轧制轧制力解析模型,获得了异步轧制条件下的轧制力和轧制力矩计算模型。
然而,由于现有冷轧数学模型再从机理上进行精度提升非常困难,为准确描述轧制过程中未知因素的影响,国内外学者将人工智能技术应用到工艺模型中。郭慧娟[3]在全梯度下降树上做了改进,基于深度LightBGM的模型实现了轧制力的预测;丛日霞[4]用蚁群-BP神经网络,实现了轧制力的预测;杨景明等[5]采用神经网络对冷连轧机轧制力进行快速预报;洪悦等[6]提出了一种基于数据驱动的轧制力设定方法;Gudur等人[7]根据现场数据和有限元模拟数据采用径向基函数神经网络模型对冷轧轧制力和力矩进行预测,并根据预测结果对神经网络模型的结构和算法进行优化;Heydari Vini[8]根据Mobarakeh钢铁公司的两机架可逆冷轧机的实际生产数据,采用BP神经网络模型预测轧制力和带刚出口厚度;魏立新等[9]针对冷连轧生产中难以建立准确的轧制力数学模型的问题,提出了基于半监督深度网络的轧制力预报模型,实现了轧制力的高精度预测。极限学习机(Extreme Learning Machine,ELM)相较于其他机器学习方法具有结构简单、计算速度快等优势,在轧制领域已有广泛应用。刘悦等[10]提出了一种具有拓扑结构自组织的极限学习机算法,实现了ELM结构和参数的自组织;曹卫华等[11]提出了一种基于灰色关联分析的ELM轧制力预报模型,通过对输入变量进行灰色关联分析,获得输入变量之间的相关性;石振桔等[12]提出了基于混合蛙跳算法优化反馈极限学习机参数的模型,实现了带钢厚度的预测。
1 轧制力模型
典型的轧制力模型有斯通模型、采利柯夫模型、柯洛辽夫模型、布兰特-福特(Bland-Ford)模型等[13]。其中,Bland-Ford模型在实际生产中得到了广泛应用,其一般形式为
P=BlcQpKTK,
式中:B为带钢宽度;lc为压扁后变形区接触弧长,与带钢入口厚度、出口厚度、轧辊直径等因素相关;QP为压扁后的外摩擦应力状态系数,与轧辊轧制长度、轧制速度等因素相关;KT为张力影响系数,与入口张力、出口张力相关;K为变形抗力,取决于钢种。
轧制力理论模型中的摩擦状态系数、带钢变形抗力等工艺参数无法准确在线实时测量且难以用理论模型精准描述,因此现有轧制力模型单纯从机理上提高精度异常困难。为此,本文提出的GA-FELM轧制力预测模型是基于冷轧生产线大量的实际生产数据拟合出来的,通过引入智能算法来改进传统模型泛化性能差的缺陷,从而提高轧制力的在线预测精度。
冷连轧机组轧制生产线结构如图1所示,其中轧制力预测系统主要选取带钢宽度、入口厚度、出口厚度、入口张力、出口张力、轧辊直径、轧辊的轧制长度、轧制速度这几个量作为输入,将轧制力作为系统的输出,即预测的目标。
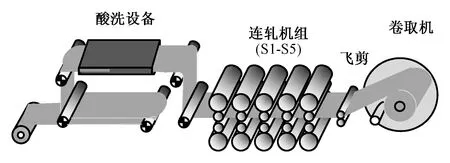
图1 冷连轧轧制生产线结构Fig.1 Structure of cold rolling production line
2 GA-FELM 预测模型
2.1 反馈极限学习机
反馈极限学习机(Feedback Extreme Learning Machine,FELM)在原有ELM的基础之上增加了一条反馈回路,将预测值和实际值的误差输入到网络之中,通过循环迭代来获得最优网络模型,反馈极限学习机算法应用在轧制力预测上的网络结构如图2所示。

图2 反馈极限学习机应用在轧制力预测上的网络结构Fig.2 Network structure of feedback extreme learning machine applied to rolling force prediction
图中,wij为输入层第i个神经元与隐含层第j个神经元Pj之间的连接权值,βj为隐含层神经元Pj与输出层神经元之间的连接权值,每个训练样本的输入向量为
xi=[xi1xi2…xi(n+1)]T,
设每个训练样本输出为yi,则输出矩阵Y为
Yi=[y1y2…ys],
设每个训练样本输出为ti,则预测输出T为
T=[t1t2…ts],
反馈回路输入的是FELM网络模型预测值和实际值的误差,误差向量e为
e=Y-T,
设隐含层的输出矩阵为H,则由图2可得
T=βH,
根据Huang G B等[14]提出的关于单隐层前馈神经网络相关理论可得,如果隐含层神经元个数和训练集样本个数相同,则对于任意的权值矩阵W和阈值矩阵b,单隐层前馈神经网络都可以零误差逼近训练样本的真实值,但是一般的训练集样本数目s比较大,为了减少计算量,单隐层前馈神经网络的训练误差可以逼近一个大于0的任意的值ε,即
‖T-Y‖≤ε,
因此,隐含层与输出层的连接权值矩阵β可以通过求解以下方程组的最小二乘解获得:
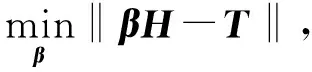
可以由上式求得矩阵β的解为
其中,H+为矩阵H的Moore-Penrose广义逆。
2.2 FELM轧制力预测流程
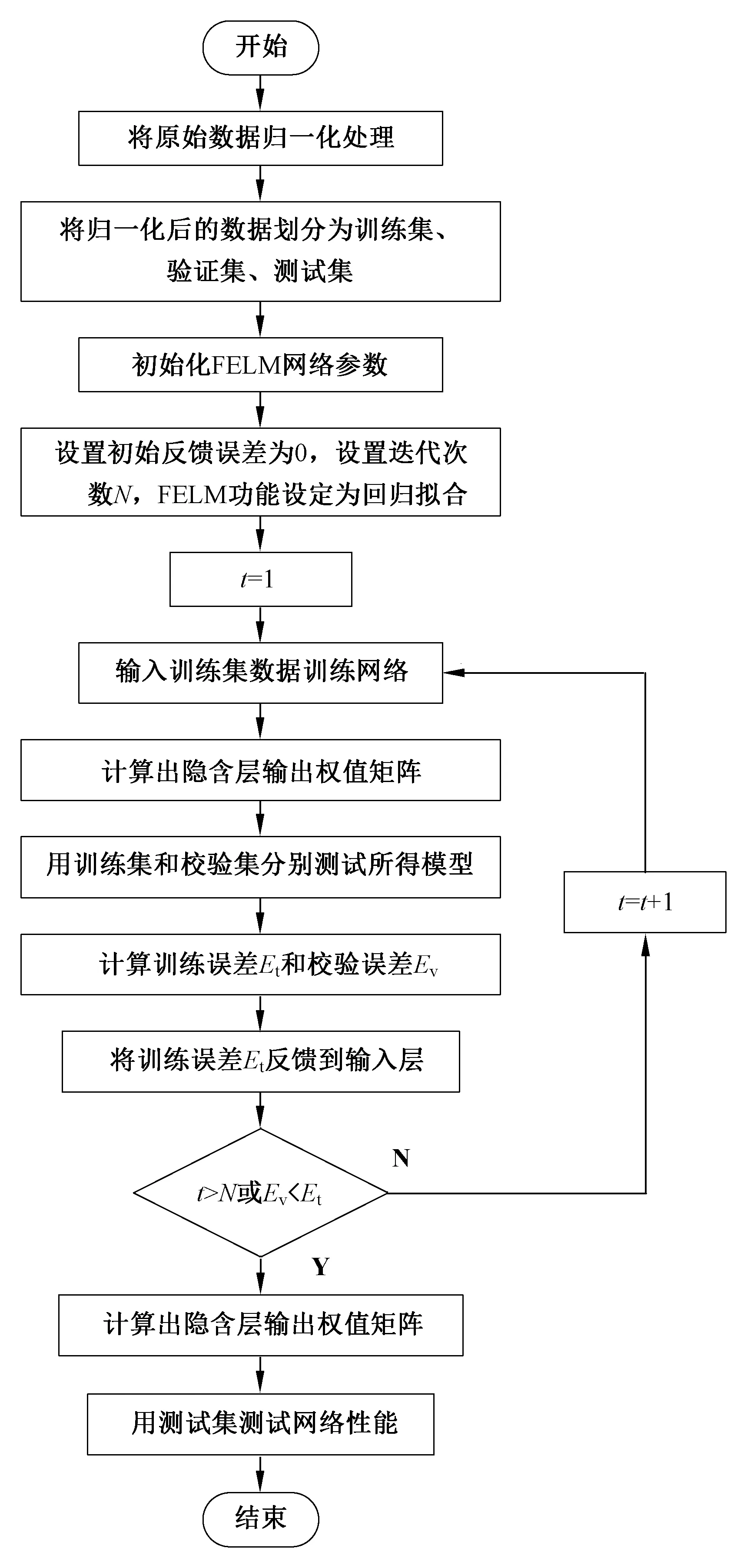
虽然在网络结构上FELM和普通ELM相比只是多增加了一条回路,但是在网络实际运行流程中FELM和ELM却有不同之处,FELM网络在轧制力预测的流程如图3所示。
FELM网络在在轧制力预测过程中的步骤如下:
步骤1:将轧制原始生产数据归一化处理,并将归一化后的数据样本分为训练集,验证集,测试集。
步骤2:初始化FELM网络参数,将初始误差全部设置为0,设置FELM网络迭代次数N,并将FELM网络功能设置为回归拟合。
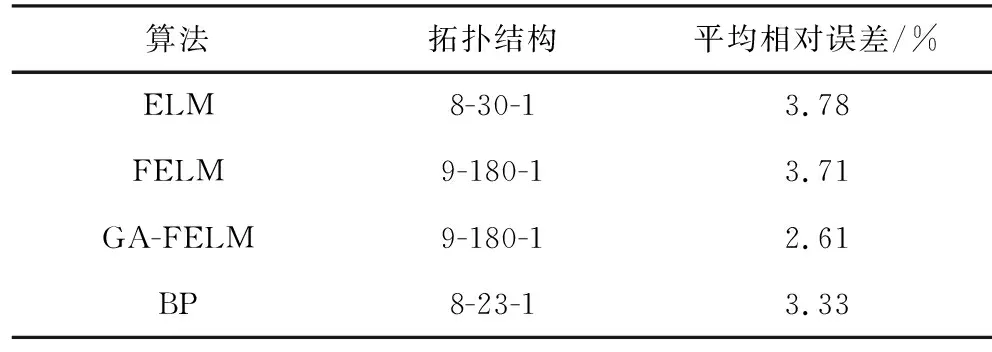
步骤3:用训练集和验证集训练网络模型,设训练误差为Et,校验误差为Ev,如果校验误差小于训练误差,即Ev 步骤4:用测试集样本测试训练好的FELM网络模型,并分析预测结果。 由于FELM和普通ELM在输入层与隐含层神经元的连接权值矩阵W和隐含层神经元阈值矩阵b的选取上没有区别,若随机选取FELM网络的初始权值矩阵W和阈值矩阵b会对模型的预测精度造成很大影响,所以需要通过智能算法对FELM网络的初始权值阈值进行优化来保证模型的预测精度,而遗传算法(Genetic Algorithm,GA)的本质是将问题参数编码成染色体后再进行优化,而不针对参数本身,从而摆脱了函数约束条件的限制;并且最优解的搜索过程是从一个集合而不是一个个体展开,大大降低了陷入局部最优的可能性,非常适用于大规模非线性问题中的参数优化,所以在初步建立的FELM模型基础之上,用GA对网络初始权值阈值进行优化,来提高网络精度,构建GA-FELM模型。 图3 FELM网络轧制力预测流程Fig.3 Process of rolling force prediction based on FELM network GA-FELM模型的运算过程如图4所示,基本步骤如下: 步骤1:确定FELM网络的拓扑结构, 并对FELM网络的W和b编码,得到初始种群。 步骤2:解码得到W和b,并将得到的W和b带入FELM网络对模型进行训练,并用测试集测试网络,得到FELM网络的预测误差。 步骤3:根据FELM网络的预测误差计算个体的适应度值,并选择适应度高的染色体进行复制。 步骤4:对选中的个体进行交叉、变异操作后产生新的种群。 步骤5:判断当前种群是否满足遗传算法终止条件,若不满足,则继续步骤2~4直到当前种群满足遗传算法终止条件;若当前种群满足终止条件则在对解码之后得到FELM最优W和b。 图4 GA-FELM模型的运算过程Fig.4 Operation process of GA-FELM model 本文以某厂冷轧现场采集的888组实际生产数据为例,把其中的700组作为训练集,94组作为验证集,剩余的94组作为测试集。其中GA-FELM中FELM部分的隐含层激活函数设置为Sigmoid函数,迭代次数N为10次,隐含层神经元个数m为180个,总体拓扑结构为8-180-1,初始权值、阈值均为随机值;GA部分的种群大小为40,种群最大遗传代数为50,交叉概率为0.8,变异概率为0.01。每个现场数据样本共采集了8个与轧制力相关的参数作为输入,分别为:带钢宽度W、入口厚度h0、出口厚度h1、入口张力T0、出口张力T1、轧辊直径Φ、轧辊的轧制长度l、轧制速度V,将测得的原始轧制力P作为模型输出的参考,并用于计算误差。用于模型训练和测试的在现场采集的部分轧制力生产数据样本如表1所示。 表1 冷轧轧制力数据Tab.1 Data of cold rolling force 为了证明GA-FELM轧制力预测模型满足实际轧制过程中对轧制力预测精度的需求,并且体现出GA-FELM模型在单隐层网络轧制力预测模型中的优势,选取全部测试集共94组数据,将GA-FELM模型分别和由传统BP神经网络以及原ELM网络建立的轧制力预测模型进行对比。通过分析各个模型的轧制力预测结果可知,GA-FELM模型具有更高的精度。表2给出了各个算法在对应拓扑结构下测试集样本数据预测值与实际值的平均相对误差,根据轧制力预测的平均相对误差表明,通过GA-FELM算法所构建的轧制力预测模型的精度明显高于BP神经网络和原ELM网络,进一步说明了GA-FELM模型在轧制力预测方面的有效性。 表2 不同算法的拓扑结构及轧制力预测平均相对误差对比Tab.2 Comparison of topological structure and mean relative error of rolling force prediction based on different algorithms GA-FELM模型与ELM模型和BP模型的轧制力预测结果对比如图5、图6所示。 图5 GA-FELM模型和ELM模型预测结果对比Fig. 5 Comparison of prediction results between GA-FELM model and ELM model 图6 GA-FELM模型与BP模型预测结果对比Fig.6 Comparison of prediction results between GA-FELM model and BP model 针对传统轧制力预测模型存在的参数强耦合、非线性等缺点,提出了一种基于GA-FELM算法的冷轧轧制力预测模型,模型中在原ELM网络中增加了一条反馈回路,构成FELM网络,并设计了GA部分以优化FELM网络的初始权值和阈值,提高模型预测精度。由实际生产数据对模型进行仿真实验,可以看出其预测精度达到了生产的基本要求,通过对样本数据的筛选和归一化处理,确定网络的最优拓扑结构以及对GA优化参数的调整,使得85%以上的样本点的相对误差控制在±5%误差带之内,预测绝对误差位于±30 t以内,性能均优于原ELM模型和传统BP神经网络模型,该方法可运用于冷轧生产现场的轧制力预报。2.3 GA-FELM结构设计

3 模型仿真与预测
3.1 模型仿真研究


4 结论
