无人驾驶方程式赛车线控制动控制策略研究
2022-06-08金鸿耀任建平
金鸿耀,李 刚,任建平
(辽宁工业大学 汽车与交通工程学院,辽宁 锦州 121001)
0 引言
随着电动汽车逐渐向智能化领域发展,汽车的智能化已成为必然的发展趋势。目前,智能驾驶车辆线控制动系统的仿真模型、控制系统、仿真实验、实车测试等方面的相关内容[1],国内外研究人员已经做了大量的研究。传统制动无法实现主动制动和制动压力精确、快速控制,所以制动系统需要线控化[2]。线控化底盘是实现无人驾驶的基本条件,线控制动系统是研究线控化底盘重要组成部分[3]。其主要包含两个方向:电子液压制动(Electronic Hydraulic Brake,EHB)与电子机械制动(Electromechanical Brake,EMB)[4]。
对于线控制动系统来说,控制算法是线控制动系统实际应用的关键所在。文献[5]以一种液压调控的线控制动系统进行建模,提出一种双层结构的控制器,上层基于深度学习获取不同路面最佳滑移率,下层采用滑模控制对最佳滑移率进行跟踪控制,实验表明相较于传统控制器,制动效果更好。文献[6]对于线控制动机电执行器系统存在非线性死区效应以及输入饱和问题,基于死区和抗饱和补偿PID控制器控制线控制动系统,仿真结果表明该控制算法使执行器系统延迟相应减少约50%,无过冲,效果明显提高。文献[7]提出了一种模糊控制与逻辑门控制结合的线控制动控制策略,仿真结果表明所提出的策略具有良好的制动控制效果,且响应快。文献[8]基于装有电子稳定程序(Electronic Stability Program,ESP)液压控制单元的乘用车,采用前馈加PID控制器对上层期望制动油压压力进行跟踪,控制主回路常闭开关阀的通断和电机的启停,实现液压跟踪控制。台架与实车测试结果表明能够较好的跟踪上层期望液压值。文献[9]应用模糊PID算法作为车辆的线控制动系统控制策略,仿真表明该算法在不同附着系数的路面上,能够保证滑移率最优,缩短了线控制动时间与制动距离。文献[10]基于装有EMB的乘用车,设计了分层式控制器,顶层控制器使用滑模加模糊控制,对期望制动力及横摆力矩求解,底层控制器以车轮为控制目标,达到协调控制的目的。仿真表明该控制策略既保证了线控制动的稳定性,又满足了车辆对横摆的要求。
上述研究大多都是基于EHB、EMB或ESP液压泵开发线控制动系统控制策略,对基于制动踏板改装的线控制动系统而开发的控制策略研究较少,难以应用于无人驾驶方程式比赛中。因此,本文以无人驾驶方程式赛车为平台,设计适用于无人驾驶方程式赛车的线控制动系统控制策略。应用增量式PID控制算法控制制动油压输出大小,并对线控制动执行机构进行控制。应用CarSim搭建车辆动力学模型,应用MATLAB/Simulink搭建线控制动控制策略,并应用CarSim/Simulink联合仿真,对线控制动控制策略进行仿真验证。
1 线控制动系统
方程式赛车的制动系统是由制动踏板、主缸、轮缸等部件组成的,相较于乘用车来说,无液压助力系统,由纯机械结构组成。中国大学生无人驾驶方程式大赛规则中规定,赛车必须保留有人驾驶模式,因此线控制动系统的设计需保留赛车原有的机械液压制动系统,对原机械制动进行线控化处理。考虑到机械制动机构的特点,设计一种适用于无人驾驶赛车特性的线控制动系统如下:在赛车的制动系统基础上加装工业舵机作为线控执行机构。将舵机安装在舵机固定吊耳上,固定在赛车驾驶舱内;舵机与制动踏板之间设计摇臂与连杆连接舵机与制动踏板,通过摇臂与连杆传递舵机转矩,带动制动踏板旋转;为了保证驾驶员制动时舵机不产生额外阻力,设计空行程结构如图1所示,在驾驶员踩制动踏板时舵机摇臂转动但不带动电机转动;舵机与摇臂之间通过法兰传递电机转矩,舵机摇臂与连杆之间使用螺栓链接;当电机旋转时,舵机摇臂拉动连杆,带动制动踏板旋转。制动完成后,舵机恢复到初始转角,制动踏板在制动主缸压力作用下复位。线控制动系统装配图如图2所示。

图1 空行程结构Fig.1 Empty stroke structure

1—制动舵机;2—舵机摇臂;3—连杆;4—紧急制动储能装置;5—制动踏板;6—制动主缸;7—制动气缸
由图2可知,无人驾驶方程式赛车的线控制动系统执行机构主要由制动舵机、舵机摇臂、连杆构成,舵机通过机械机构与原车制动踏板相连,通过控制舵机的旋转角度来控制赛车的减速强度。
2 线控制动控制器设计
2.1 线控制动控制逻辑
赛车的实际纵向速度是通过车辆上安装的4个轮速传感器采集的信号进行处理后获得。将期望纵向速度与实际纵向速度做差可得到某一时刻的速度差值及差值变化率,对差值进行判定,若值为负则需要减速。将计算得出的减速度值及当前时刻的减速度值作为增量PID控制器的输入,经控制器处理后输出制动减速度变化值,结合上一时刻减速度大小可得出当前时刻的期望制动减速度大小,通过理论公式计算可得制动油压大小,并控制制动电机旋转至一定的角度,输出制动油压。根据电机旋转角度与制动油压关系曲线设计电机控制模块,控制制动电机旋转,实现赛车减速控制。线控制动系统控制逻辑如图3所示。

图3 线控制动控制逻辑Fig.3 Brake-by-wire control logic diagram
2.2 增量式PID控制算法
PID控制算法以简单、实用、稳定而著称,是可以根据被控对象输出的反馈值来进行校正的闭环控制,其主要特点是可以不考虑被控对象的数学模型,根据积累的经验对PID的3个参数在线的调试,可得到理想的结果。PID控制系统如图4所示。

图4 PID控制系统原理图Fig.4 PID control system schematic diagram
其中,r(t)为输入信号,c(t)为输出信号,u(t)为PID控制器输出信号,e(t)为输入信号与输出信号的偏差值。PID控制器的控制率微分方程为
(1)
式中,e(t)=r(t)-c(t),kp是比例增益系数,ki是积分增益系数,kd是微分增益系数。
增量式PID控制是一种递推式的控制算法,通过当前时刻被控对象的值和前一时刻被控对象的值做差,将差值作为新的控制量对系统进行控制[11]。与PID控制不同,增量PID控制输出仅与当前时刻误差和前一个时刻误差有关,相较于PID控制累计误差相对较小,控制灵敏。增量PID算法原理为
ΔU(k)=U(k)-U(k-1),
(2)

(3)
式中,e(k)表示期望速度与实际速度的差值,kp、ki、kd分别代表各自变化量的比例系数,U(k)为控制器输出的控制量,ΔU(k)为控制器输出变化值,T为采样周期,Ti、Td分别为积分时间与微分时间。将期望纵向速度与实际纵向速度的差值变化率输入到增量PID中,输出的ΔU(k)与上一时刻的制动减速度值累加,最终输出制动减速度大小。将制动减速度换算成制动力大小,依据主缸与轮缸的特性转换为制动油压大小,制动力与制动减速度关系式为
Fb=maxb=Fzsz,
(4)
(5)
式中,Fb为制动力大小,m为整车质量,axb为制动减速度,Fzs为车辆静载,z为制动强度。
2.3 制动电机控制
线控制动控制器的输出为期望制动油压,由制动电机旋转一定的角度来实现制动油压的输出。依据线控制动系统执行机构的特性,可得出制动踏板最大工作角度,依据连杆机构的传递比可以得出制动电机的工作角度范围。通过对线控制动系统标定可得电机旋转角度对应制动油压大小,如图5所示。

图5 制动压力大小随电机角度变化曲线Fig. 5 Variation curve of brake oil pressure with motor angle change
所选电机的控制方式为PWM控制,通过控制频率的变化实现对电机角度的控制。当控制器输出期望油压时,电机旋转至相应的转角,带动主缸输出制动油压。电机角度控制如图6所示。
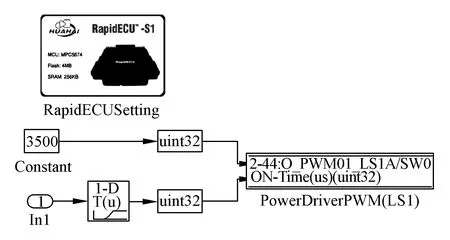
图6 制动电机控制模块Fig.6 Brake motor control model
3 联合仿真模型
3.1 联合仿真模型框架
车辆的车体模型、动力传动模型、制动系统模型、轮胎模型等模型使用CarSim软件搭建。由于整车的动力为双电机独立驱动,而CarSim中的动力单元模型为内燃机模型,故将CarSim整车模型动力来源设置为外部输入,使用Simulink搭建电机模型作为赛车动力输入给CarSim模型中。忽略空气阻力等因素,主要考虑车辆纵向速度控制。无人驾驶方程式赛车仿真模型总体框架如图7所示。
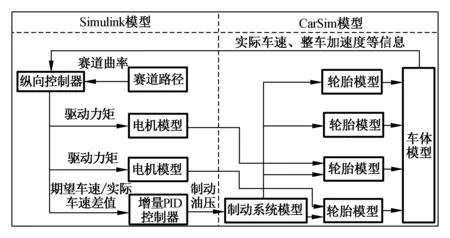
图7 仿真模型总体框架Fig.7 Overall framework of simulation model
根据无人驾驶方程式赛车的实际参数,搭建整车仿真模型,仿真模型的部分参数如表1所示。
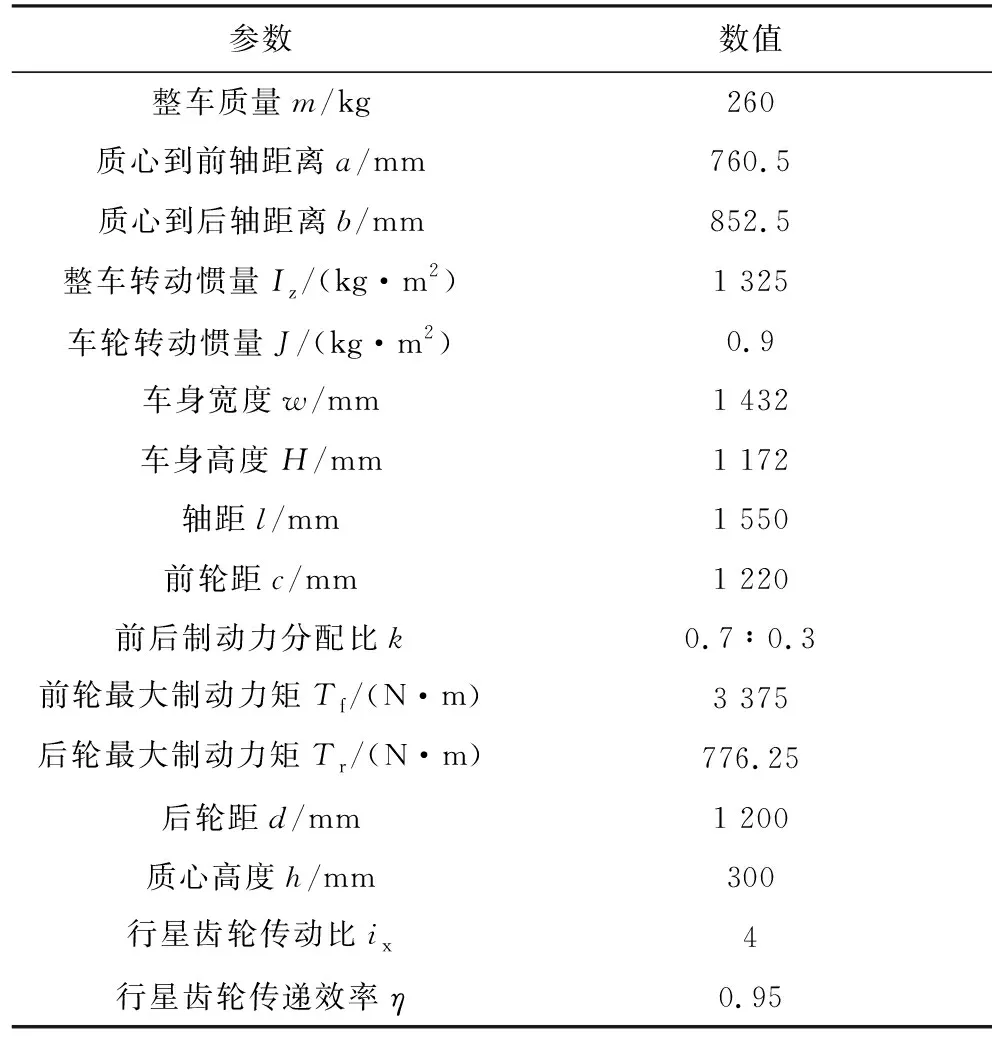
表1 整车参数Tab.1 Vehicle parameters
无人驾驶方程式赛车的驱动形式为双电机后轮独立驱动,对电机标定可得出电机的外特性曲线,进而搭建加速控制器模型。由于本文主要研究线控制动系统的控制策略及其准确性,故加速控制器不做过多赘述。
3.2 CarSim/Simulink联合仿真模型
使用Simulink搭建无人驾驶方程式赛车线控制动控制器,将线控制动控制器输出的制动油压作为CarSim模型与制动电机控制模块的输入,CarSim模型输出实际纵向速度和实际整车加速度形成闭环控制。CarSim/Simulink联合仿真模型如图8所示。

图8 联合仿真模型Fig.8 Co-simulation model
纵向速度控制器输出的期望纵向速度与CarSim反馈的模型实际纵向速度做差值得到速度差值,对差值进行判定:若为正值则证明此时赛车需要进行加速处理,经过加速控制器处理后输出电机扭矩来使赛车加速;若值为负值则证明此时赛车需要进行减速,将得到的差值变化率作为增量PID的输入,根据上述所提到的线控制动控制策略,使用Simulink搭建线控制动控制器。控制器如图9所示。

图9 线控制动控制器Fig.9 Brake-by-wire controller
4 仿真与实车实验
为验证所设计的控制策略的有效性与实用性,将所提出的控制策略使用CarSim与Simulink进行联合仿真验证,对比了本文提出的控制策略与PID控制策略的差异,并进行了实车测试。仿真工况选择CarSim内置的Autocross测试工况,工况路径如图10所示。

图10 仿真工况Fig.10 Simulation conditions
实车测试搭建与仿真工况相同的赛道,使用实验室研发的无人驾驶方程式赛车为测试平台,如图11所示。在原测试车的基础上安装线控制动执行单元,如图12所示。整车控制器使用华海科技快速原型控制器Rapid-S1,采集并保存车辆运行时实际纵向车速、制动油压值、电机旋转角度等信息。

图11 测试车辆Fig.11 Test vehicle

图12 线控制动执行单元Fig.12 Brake-by-wire execution unit
测试工况的弯道半径已知,根据转弯半径可计算出赛车转弯时最大理论速度,即
(6)
其中:vmax为理论上允许的最大纵向速度;g为重力加速度;μ为路面附着系数;ρ为路径曲率。曲率为转弯半径的倒数。根据已知的测试工况转弯半径,可得测试道路曲率如图13所示。

图13 道路曲率曲线Fig.13 Curvature curve of the road
图13为道路曲率曲线图,由实验数据可得测试工况最大曲率为0.25,仿真实验工况与实车测试工况均为单一附着路面,附着系数为0.85,路面平坦无起伏,根据测试工况道路曲率,通过式(3)计算可得赛车在不同曲率下的最大纵向速度,由于规则对电机功率的限制以及赛车实际性能,最大纵向速度限制在50 km/h,以此得出赛车的期望纵向速度。赛车的横向控制由横向控制算法控制,纵向速度控制由加速控制模块与文章中提到的线控制动模块控制,仿真时只考虑纵向速度的控制,不考虑横向控制等因素的影响。仿真与实车测试结果如图14所示。

由图14(a)的实验数据可以得出,减速过程分别为3.5~4.3 s、9~9.5 s、16.3~17.6 s、23.1~24.3 s、30.5~31.7 s、34.2~35 s、43.8~44.1 s、48.3~48.5 s、69.1~71.1 s。在赛车减速过程中,增量PID控制策略较比PID控制策略的仿真车速曲线更加贴合期望车速曲线,响应延迟时间不超过200 ms,反应灵敏。由于执行器存在延时,实车测试结果比仿真延迟不超过300 ms。由图14(b)的实验数据可得,本文提出的控制策略跟踪误差最大值为6 km/h,跟踪误差在6 km/h以内变化,而PID控制策略最大跟踪误差为11 km/h,跟踪误差在11 km/h以内变化,由于赛车横向控制及其他因素的影响,实车测试赛车减速时纵向速度跟踪误差在9 km/h以内变化。在实车测试中45 s和50 s附近的两次减速,由于场地和车辆自身横向控制算法等因素的影响,导致纵向速度跟踪误差偏大。总体可得本文提出的控制策略控制精度高于PID控制策略,且实车测试跟踪效果良好。由图14(c)可知,当线控制动控制器输出油压控制信息后,制动电机旋转相应的角度,使主缸输出制动压力。响应速度较快,在1.5 s以内能够完成0°至130°的角度变化,且电机的控制平稳不抖动。图14(d)为实车测试线控制动控制器控制下制动油压实际大小,最大制动油压约为5.4 MPa。控制器根据解算出的实际需求输出相应的制动压力,并将信号输出给制动电机控制模块,由制动电机执行带动原车制动踏板,输出制动油压。制动油压控制平稳,线控制动执行单元发出指令到油压产生延迟不超过300 ms。
5 结论
本文基于无人驾驶方程式赛车线控制动系统,设计了一种以增量PID为主要控制算法的线控制动系统控制策略,控制制动油压的输出。应用CarSim与Simulink联合仿真并进行实车测试,验证所设计的控制策略的有效性与实用性。仿真结果与实车测试结果表明:该控制策略在赛车减速时能够较好地跟踪纵向期望速度,跟踪误差不超过6 km/h,响应延迟不超过200 ms,实车测试减速时纵向速度跟踪误差不超过9 km/h,响应延迟不超过500 ms,响应快,控制精度高;制动电机控制可以在1.5 s以内完成0°~130°的角度变化,且电机的控制平稳不抖动。该线控制动控制策略提高了无人驾驶方程式赛车减速时纵向速度跟踪精度,实车测试表明减速时跟踪效果良好,具有一定的实际应用价值。
