堆取料机防碰检测系统多毫米波雷达标定方法研究
2022-06-08王立成孔德明
王立成,孔德明,*,沈 阅,曹 帅,张 钰
(1.燕山大学 电气工程学院,河北 秦皇岛 066004;2.河北燕大燕软信息系统有限公司,河北 秦皇岛 066000)
0 引言
近年来,随着毫米波技术的不断发展,毫米波雷达的检测精度不断提高,由于其对雨、雪、雾、尘等恶劣环境具有很高的适应性,因此可以应用在大型散料堆场堆取料机的防碰检测和成像中。在实际应用中,需要利用多个毫米波雷达多角度扫描弥补单个毫米波雷达的视野盲区,这不可避免涉及到多个毫米波雷达之间的联合标定。
毫米波雷达应用在工业中的时间较短,虽然国内外对毫米波雷达联合标定方法的研究还比较少,但是对于双目摄像机和激光雷达等传统传感器的标定技术已经相当成熟,许多在不同场景下的标定方法对毫米波雷达的联合标定具有借鉴意义。这些标定方法根据标志物的特征类型主要可以分为两类:1)基于特征点的标定方法;2)基于特征直线的标定方法。
基于特征点的标定方法通过不同传感器捕捉相同标志物的特征点进行匹配从而获取彼此的相对位姿参数。李为民等人提出了一种基于一维标定点标定双目相机的算法[1],通过拍摄靶子在空间中多个位姿的图片结合靶子上两个编码点间的距离约束完成双目相机的标定,具有可现场标定、多相机同时标定的优点。郭清达等人[2]的标定方法中以棋盘为标志物,对棋盘标靶提取特征点,根据张氏标定获取双目视觉相机的内外参数,再通过迭代最近点算法对特征点进行匹配得出补偿矩阵,提高了双目视觉标定的精度。虽然文献[1-2]方法中的标志物简易,特征明显方便现场标定,提高了标定精度,但是基于特征点的标定需要传感器对标志物特征点检测有较高稳定性和准确性,根据毫米波雷达对障碍物的检测特性,在大场景下面积较小的障碍物其雷达散射截面积较小难以检测,容易淹没在噪点中,无法区分出来;对于面积较大的标志物,由于毫米波雷达数据点集具有稀疏、散乱的特点,无法确定标志物在不同毫米波雷达中的反射点是否应该重合,因此利用特征点对毫米波雷达进行标定容易造成较大误差。
相比特征点,直线特征包含更丰富的信息,因此除了基于特征点的标定方法外,很多学者针对基于特征直线的标定方法展开了研究。俞奇奇等人[3]采用了一个可以精确控制的伺服旋转平台,通过设计激光雷达的固定位置减少标定参数,并以墙面作为标定物实现激光雷达坐标系的标定。韦邦国等人[4]以直角墙面作为标志物,利用最小二乘法拟合出墙面的直线特征并根据重合准则计算出两二维激光雷达间的相对横摆角和横纵方向偏移量,最后通过遗传算法获得全局优化的标定参数完成标定。由于直线特征比点特征更容易区分,且在直线拟合过程中降低了传感器分辨率对标定的影响,因此基于直线特征的标定方法一定程度上提高了标定精度,非常适合用于处理稀疏、散乱以及分辨率相对较低的毫米波雷达数据。但传统的最小二乘法拟合效果受噪点影响较大,当存在偏差较大的噪点时,拟合直线容易偏离最佳拟合位置,显然无法应对工业现场数据,因此需要一个对噪点有较强抗性、能够精确提取直线特征的直线检测方法。
直线检测在计算机视觉与图像分析领域一直是热门的研究问题[5],目前存在的直线检测方法可以分为两类[6]:1)感知分组;2)霍夫变换(Hough transform,HT)。其中感知分组更多运用在图像研究领域,该方法将直线描述为存在足够相似和共线分量的连通区域。BURN等[7]首先提出了基于梯度方向的直线检测方法。在他们的方法中,直线被检测为一个直线图像区域,其中内部像素(组件)共享大致相同的方向(相似性)。然而,毫米波雷达数据分布稀疏、散乱,并不适合准确计算梯度方向,因此直线检测效果欠佳。AKINLAR等[8]提出的直线检测方法中,虽然能够直接从边缘像素检测直线,检测速度明显提高,但是忽略了直线周围点对其精确定位的作用,在噪声较大的情况下精度较差。
相比感知分组,HT则是从不同的角度解析直线特征。HT将点集映射到参数平面进行投票,多个共线点的投票对象中包含同一个参数单元,这使该参数单元所获票数呈现局部极大值的特征,通过搜索峰值得到直线参数从而反解出直线方程。标准的HT在检测速度和精度上有缺点,但前人们经过多年的研究提出了许多优秀的改进算法。XU等人[9]提出随机霍夫变换(Randomized Hough Transform,RHT),从待检测点集中随机选取两点进行映射投票,将HT中的映射方式由一对多转化成了多对一,避免了大量无用计算从而提高计算效率,被广泛运用在车道线检测等领域[10-13];在精度方面,郭斯羽等人[14]提出HT与双点移除p-最小二乘法(p-Least Squarest with Dual Removal,pLS-DR)结合,通过较粗分辨率下的HT检测出直线的大致位置并获取直线附近的点作为待拟合点集,然后利用pLS-DR对待拟合点集进行拟合和迭代,每次拟合后同时去除正、负两个方向上一对误差最大的数据点,直到点集的当前点数与初始点数之比低于比例阈值时输出直线方程。该方法结合了HT在无启示信息的前提下对直线粗检测的鲁棒性以及最小二乘法对点集更精确拟合的优点,同时pLS-DR有效减少了噪点对拟合的影响。
基于以上分析,根据现场条件及毫米波雷达成像特点,本文提出一种优化的基于坝基直线特征的毫米波雷达现场联合标定方法。以堆取料机走行坝基为标志物,根据坝基的直线特征实现多个毫米波雷达的联合标定;为了提高对坝基边缘直线特征的检测精度,本文提出使用RHT与改进的pLS-DR相结合的直线检测方法对坝基的直线特征进行提取;最后通过遗传算法进行全局优化。实验结果表明改进的直线检测方法在本文场景中相对于传统算法检测精度明显提高,标定方法标定精度较高。
1 标定准备工作
1.1 堆取料机防碰检测系统
本文的标定方法是针对大型散料堆场中堆取料机防碰检测系统中多个毫米波雷达现场标定的方法。系统硬件包括堆取料机、毫米波雷达、坝基(含轨道),其中堆取料机的主要部件又包括斗轮、臂架、回转中心和走行装置。在堆取料机作业过程中斗轮负责取料,臂架通过回转中心和走行装置进行回转、行走等作业动作。堆取料机防碰检测系统的主要传感器是毫米波雷达,6个毫米波雷达分布在堆取料机臂架多个方位,对臂架回转平面进行多角度扫描,安装位置为:左侧安装3个雷达,其中雷达1安装在臂架前部负责扫描左侧前部范围,雷达2和雷达3安装在臂架中部分别负责扫描臂架左侧的中部范围和后部范围;右侧3个雷达与左侧相似,均是一个安装在前部两个安装在中部,并分别扫描臂架右侧前、中、后部范围。以雷达1和雷达2为例描述标定方法,引入3个坐标系:臂架坐标系O0-X0Y0,雷达1坐标系O1-X1Y1,雷达2坐标系O2-X2Y2。系统硬件平台如图1所示,图中扇形为雷达的扫描范围。
1.2 标定数学模型
一般情况下标定参数主要包括横摆角、水平角、俯仰角以及三维空间平移量。在堆取料机防碰系统中,毫米波雷达的俯仰角和水平角可用水平尺和重锤测量并调整至一致[15],因此可认为各个雷达拥有相同的俯仰角和水平角;由于毫米波雷达安装位置的高程值相差较小(<1 m),远远小于成像范围([0,250 m)),且成像为二维点集即只反映X、Y分量而不反映高程值,因此可忽略安装位置高程值的影响认为雷达均被安装在同一个平面上。所以标定需要确定的位姿参数为横纵方向平移量Δx、Δy和相对横摆角Δβ,则标定数学模型如图2所示,其中β1和β2分别是O1-X1Y1和O2-X2Y2相对O0-X0Y0的横摆角;Δx、Δy分别是在O0-X0Y0中O2-X2Y2相对O1-X1Y1的横纵方向平移量。
空间某点M在O0-X0Y0,O1-X1Y1和O2-X2Y2中的坐标分别为M0(a0,b0),M1(a1,b1)和M2(a2,b2)。M0、M1和M2的关系为
其中:R10、R20分别为M1到M0和M2到M0的旋转矩阵;T10和T20分别是对应的平移矩阵。但R10、R20和T10、T20是通过堆取料机回转编码器以及通过工具测量得到的,由于编码器以及测量误差的影响,容易造成严重的成像重影。为解决此问题,直接从成像着手,通过标定得到雷达间相对位姿参数,进一步得到对应的相对旋转矩阵R21和相对平移矩阵T21,则有
变换后可得
M0=R10R21M2+R10T21+T10,
(1)
通过式(1)即可将多个雷达根据雷达间的相对位姿参数转换到臂架坐标系中,降低成像重影。
1.3 标定原理
分别在臂架旋转过程中采集到t1和t2时刻坝基的扫描数据,根据运动的相对性可知,当视角与臂架保持相对静止时,旋转运动表现为坝基绕回转中心旋转,记坝基(t1)和坝基(t2)分别为t1、t2时刻坝基的位置,L(t1)和L(t2)为两时刻坝基的边缘直线,L(t1)、L(t2)、交于Q点。堆取料机和坝基的位置关系如图3所示。

图3 不同时刻下堆取料机与坝基的相对位置图Fig.3 The relative position between the stacking and retrieving machine and the dam foundation at different time
进一步将t1、t2时刻雷达1检测到的坝基边缘直线分别记为L1(t1)、L1(t2),雷达2检测到的坝基边缘直线分别记为L2(t1)、L2(t2),它们在O0-X0Y0中的位置如图4(a)所示。由于雷达1与雷达2之间存在相对横摆角Δβ,因此在同一时刻下两雷达检测到的直线存在夹角,该夹角即为相对横摆角Δβ。分别设
L1(t1):y=k11x+d11,
L2(t1):y=k21x+d21,
L1(t2):y=k12x+d12,
L2(t2):y=k22x+d22,
根据正切差角公式有
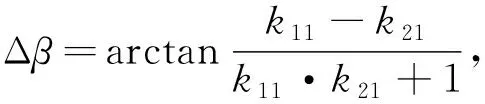
(2)

(3)
其中,R21为O2-X2Y2到O1-X1Y1的旋转矩阵。



(4)
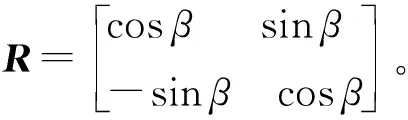

d′=Z(β,k)·d,
(5)
其中,
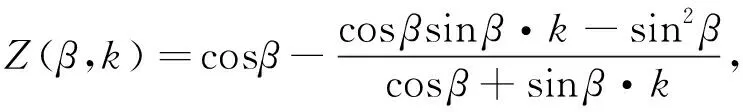
(6)
式(5)、(6)描述了直线方程截距在坐标系旋转前后的关系。根据这一关系,将雷达2坐标系旋转Δβ角度后,坝基边缘直线L2(t1)、L2(t2)的方程变为
其中:

(7)

(8)
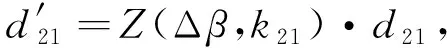
(9)

(10)
(Δx,Δy)=Q′(L1)-Q′(L2),
(11)
根据式(7)~(10)所述的关系,上式可表示为

(12)

(13)
最终根据式(2)、(3)和式(12)、(13)得到两雷达间的相对位姿参数[Δβ,Δx,Δy],旋转矩阵R21和平移矩阵T21。
1.4 标定数据采集
根据标定原理,数据采集实验为:采集在多个扫描角度下坝基的数据,以雷达1和雷达2为例,为使坝基在两雷达成像中的直线特征更加明显,控制堆取料机保持走行位置不变,俯仰角为0°,回转角从20°回转到60°,连续采集两个雷达在回转过程中的数据。其中,毫米波雷达近距离的检测分辨率为0.39 m(0~70 m),远距离检测分辨率为1.79 m(>70 m)。
2 坝基边缘直线检测
毫米波雷达数据是稀疏、散乱的二维点集,采集的数据中坝基的边缘点并非严格共线,且受雷达远距和近距的检测视角、检测分辨率不同的影响,雷达数据伴随较多噪点,因此准确提取坝基边缘直线特征是提高标定精度的关键。
2.1 RHT直线检测
RHT是在HT的基础上提出的改进算法,其检测思想与HT相同,均是根据笛卡尔坐标系中的直线与参数平面中的参数点一一映射的关系,在参数平面对参数点进行累加统计,将图像域的全局模式检测问题转化为参数空间[1 6]的高效峰值检测问题。不同的是HT的映射直线来源于穷尽经过每一点的每一直线,属于一对多,而RHT的映射直线来源于随机选取两点所确定的直线,属于多对一,大大降低了计算量。直线在参数平面的映射如图5所示。

图5 映射关系图Fig.5 Mapping diagram
其中,l:y=k·x+d为笛卡尔坐标系下的直线,C(θ1,r1)为直线映射到参数空间中的点,k、d分别为直线l的斜率和截距,θ1为直线l的法线的方向,r1为坐标原点到直线l的距离。映射过程中,将参数平面的横纵坐标按照一定的间隔量(Δθ,Δr)化成二维网格,(Δθ,Δr)称为分辨率,每个网格作为参数单元统计落入其中的参数点,这一过程也称为投票,最终通过搜索票数峰值所对应的参数单元完成直线检测。
RHT步骤可以描述为:1)不断从待检测点集中随机选取两点,将两点所确定的直线映射到参数平面,映射所对应的参数点(θ,r)的计算如式(14)~(15)所示,其中,随机选取两点坐标(x1,y1)和(x2,y2)确定的直线方程为y=k·x+d,(xo,yo)为原点到直线的垂足(以下简称垂点)。2)当存在参数单元所获票数达到一定阈值时认为该参数单元存在直线,检测的直线计数加一,同时将该直线上的点删除,减少后续计算量,直到检测的直线数量达到设定值或者点集清零时停止检测。
r=x1sinθk-y1cosθk,
(14)

(15)
2.2 RHT结合改进的pLS-DR
RHT提高了检测速度,但并没有提高准确度,其检测精度仍然受限于分辨率(Δθ,Δr),尽管提高分辨率可以提高直线检测的精度,然而当Δθ和Δr过分细化时不严格共线的“共线点”的投票可能分散到其他参数单元,从而无法积累足够的票数造成直线检测失败。
为提高直线检测精度,将RHT与pLS-DR结合,通过RHT提高直线检测速度,结合pLS-DR提高检测精度。使用较粗分辨率下的RHT检测出直线的大致位置并获取距离该直线ε范围以内的点作为待拟合点集,然后利用pLS-DR对待拟合点集进行拟合迭代,每次拟合后同时去除正、负两个方向上一对误差最大的数据点,直到点集点数与初始点数比值小于比例阈值时结束。
但是传统的pLS-DR对本文场景中坝基边缘直线的拟合存在一些缺陷:获取直线附近的点集进行拟合时,拟合效果对ε的取值比较敏感,ε较大时虽然减少了遗漏共线点的可能,但是大量增加了噪点的引入,在比例阈值p不变的情况下,最终保留的点集包含的噪点数量会增加从而导致拟合直线位置出现偏差;若ε较小,则可能遗漏共线点,同样导致拟合结果无法回归到准确的直线位置。
根据实验分析,造成以上问题的原因如下:
1)RHT检测的直线由于分辨率的限制往往不能反映准确的直线位置并且与最佳拟合位置之间具有一定的夹角,在这一夹角的影响下距离直线垂点较远的共线点偏离检测直线的距离更大,需要更大的ε值才能将其引入待拟合点集。
2)毫米波雷达在近距离扫描范围内的反射点更加密集,噪点也更多,而远处的反射点则相对稀疏,共线点也更少。因此当ε较大时,更多地引入了近处的噪点,远近点数的不均衡导致在拟合时拟合直线可能偏向近处噪点、远离远处的共线点,导致远处的共线点由于相对拟合直线的误差更大而被去除,增加了噪点的比例使拟合效果更不理想。
为解决以上缺陷,对pLS-DR提出以下两点改进:
1)设置夹角阈值ΔθLS。使用较小的ε值减少引入近距离范围噪点,同时设置夹角阈值ΔθLS进行筛选:当某一点与检测直线垂点的连线相对于检测直线的夹角小于夹角阈值ΔθLS时,将其引入待拟合点集。由于直线的偏移主要来自于RHT的分辨率,所以可取ΔθLS≈Δθ。
2)使用两次pLS-DR。根据第一次pLS-DR回归的直线方程再进行一次拟合迭代,确保直线回归到更准确的位置。
根据以上两点,RHT结合改进的pLS-DR直线检测主要步骤如下:
1)使用RHT对待检测点集进行直线检测,得到检测直线的方程y=kj·x+dj,j=0,1,…,j表示第j次迭代,将RHT检测得到的直线视为第0次迭代所得直线。

3)给定保留数据点数比例阈值p,计算最终保留的点数Nf=pN0,N0为初始点数。
4)使用最小二乘法根据点集Pj拟合得到新的回归直线y=kj+1·x+dj+1,最小二乘法回归公式为
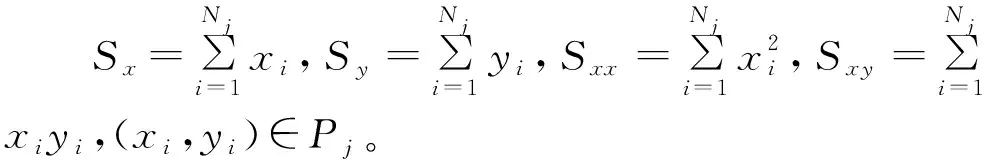
5)求取Pj中每个数据点与回归直线之间的带符号误差ei,将最大正、负误差的一对数据点移除,剩下的点集记为Pj+1={(xi,yi)|1≤i≤Nj+1},Nj+1=Nj-2。误差ei表达式为
6)如果Nj+1≤Nf,则返回直线方程作为回归结果;否则至步骤2)。
7)将6)返回的直线方程作为初始直线位置,再使用一次pLS-DR进行迭代拟合,即以6)返回的直线方程作为1)中的直线y=kj·x+dj再重复步骤2)到6),将这次回归的直线方程作为最终的直线方程输出。
改进后的方法在收集待拟合点时,既能减少遗漏远距离共线点的可能,也减少了近距离噪点的引入,使直线检测更加准确。
3 标定参数的计算及优化
3.1 标定参数计算
以雷达1和雷达2的标定为例,将采集的数据按一定时间间隔选出32帧数据,使用上一章的直线检测方法对这些数据进行检测,得到32组数据,每组数据包含了同一时刻下两组分别在雷达1和雷达2坐标系中的坝基边缘直线方程。根据这32组数据按式(3)计算得到的雷达相对横摆角Δβ,将32组数据按照不同的选择两两搭配形成177对组合,每对组合可按照式(10)计算出1组(Δx,Δy),结果如图6所示。计算结果显示,不同方程组解算出来的相对横摆角之间有一定的差异,不同的组合计算的(Δx,Δy)之间也存在一定的差异。

图6 多组数据计算结果图Fig.6 Calculated results of multiple groups of data
产生差异的主要原因是检测的坝基边缘直线方程受毫米波雷达检测分辨率相对较低、反射点散乱性以及噪点的影响从而与真实位置存在一定偏差,进而使计算得到的相对位姿参数产生误差。为了尽可能降低成像重影,采用遗传算法对标定参数进行优化,使标定结果趋向于全局最优。
3.2 基于遗传算法的参数优化
遗传算法是采用生物选择和遗传学机制的全局自适应概率的搜索算法[17]。无需指定搜索规则,能够提供通用的优化框架达到全局最优,避免落入局部最优的陷阱。
使用遗传算法首先需要确定目标函数。同一时刻下,根据雷达1检测到的坝基边缘直线转换到臂架坐标系后,所得直线方程为l1:y=k1·x+d1,根据雷达2检测到的坝基边缘直线转换到臂架坐标系后,所得直线方程为l2:y=k2·x+d2,如图7所示。
臂架坐标系原点到两直线的垂足分别为A(xoA,yoA)、B(xoB,yoB)两点,其坐标的表达式为
理论上来说,A和B应该完全重合,但是由于误差存在,A、B没有重合。A和B的长度DAB可作为衡量两个坐标系位姿关系准确性的指标。DAB的表达式为
以3.1节得到的32组数据作为样本,得到最终优化的目标方程:


图7 DAB示意图Fig.7 DAB diagram
根据确定好的目标函数,定义U=[Δβ,Δx,Δy],则优化问题转化为求解F(U)的最小值对应的U值。遗传优化算法步骤如下:
1)初始化。设定初始种群Uini、上边界Uub,下边界Ulb。上边界取多个位置中的最大值,Uub=[-0.012 1,0.99,11.69],下边界取最小值,Ulb=[-0.014 3,0.001,9.7],在上边界与下边界之间以一定间隔设置多个初始种群。其他参数设定如下:交叉概率为0.8,种群大小设置为50,最大遗传代数为200。
2)计算F(U)的值并更新F(U)。
3)重复步骤2)直到满足循环条件,循环条件设置为λ>φ,λ为迭代次数。
4 实验结果及分析
4.1 直线检测算法实验分析
直线检测实验分析以雷达1和雷达2对坝基的扫描数据为例。同一帧数据的不同处理结果如图8所示。其中,图8(a)、(b)使用pLS-DR进行拟合,距离阈值ε分别设定为2 m和4 m,比例阈值均为p=0.6。在使用pLS-DR进行拟合时,在ε=2下收集的是RHT检测直线附近2 m内的点作为待拟合点集进行拟合迭代,但是在相同的偏移角度下,远距离点比近距离点相对RHT检测直线的距离更大(可能大于2 m),因此收集的远距离共线点数较少,如图8(a)所示,最终的拟合位置虽然比RHT检测直线的位置更贴近共线点但是仍然存在较大误差;若设置ε=4扩大搜索范围,可收集更多远距离点共线点,但是由于近距离点更密集,收集的近距离点数远大于收集的远距离点数,其中也包含较多噪点,因此在拟合迭代过程中受噪点的影响,拟合直线可能更偏向于噪点,远离远距离共线点,导致远距离共线点不断被作为最大误差值点去除,最终的拟合位置也不理想,如图8(b)所示。
改进的pLS-DR由于引进了夹角阈值ΔθLS,在相同的比例阈值p下,远距离点即使距离直线更远也能通过夹角阈值ΔθLS判定为待拟合点,因此在ε=2下仍然可以收集到更多远距离点。更多的远距离共线点使最终的拟合效果更接近理想位置。此外,进行两次拟合迭代保证了RHT检测直线偏移较大时也能回归到更准确的位置。改进的pLS-DR最终保留的拟合点中共线点明显更多,拟合效果也更贴近共线点,如图8(c)所示。

4.2 标定参数优化结果分析
为防止遗传算法陷入局部最优,在上边界Uub,下边界Ulb之间以相同的间隔量u=[0.002 7,1.065 6,1.863 6]设置了4个初始种群Uini,不同的Uini代入遗传算法后计算的结果如表1所示。

表1 遗传算法计算结果Tab.1 Results of genetic algorithm
不同的初始种群Uini的计算结果大致相同,选择目标函数最小值对应的参数作为标定结果,即U=[-0.013,0.458,10.931]。比较标定算法计算结果与实际测量值,结果如表2所示。表中测量值为多次测量的平均值,J12表示雷达1和雷达2的欧氏距离。根据数据分析结果,Δx的误差为0.228 m,Δy的误差为0.16 m,两雷达之间的欧式距离误差为0.152 8 m,小于毫米波雷达的检测分辨率(0.39 m),满足工业需求。
结合相对位姿参数与式(1)、(3)、(13)可将雷达1、雷达2的数据转换到臂架坐标系中。标定后不同回转角度下的成像效果如图9所示。在不同角度下两雷达检测到的坝基边缘重合度较高,其中一些局部细节也能相契合。
最后,将标定方法推广到其他4个雷达上,即可实现多个雷达的联合标定。
5 结论
本文提出了一种针对堆场堆取料机防碰检测系统中多个毫米波雷达的现场联合标定方法:利用直线检测算法提取多个角度下坝基的直线特征,根据多组直线特征形成的几何约束计算出雷达相对位姿参数,并通过遗传算法对相对位姿参数进行全局优化。该标定方法解决了毫米波雷达在散料堆场现场标定中一般标志物难以识别的问题,标定精度较高。其中,提出了一种改进的直线检测算法,该算法在收集拟合点时增加了角度阈值进行判断,从而能够收集到更多远处的共线点,提高了直线检测精度,更适合处理稀疏、散乱的毫米波雷达数据。实验结果表明,根据标定方法计算得到的参数与实际测量值的误差控制在0.23 m以内,小于毫米波雷达检测分辨率(0.39 m),精度较高,标定后成像重合度较高,满足工业需求。
