非线性磁悬浮转子系统的不平衡响应分析
2022-06-08刘明政葛萍萍张雁翔姚俊夫王念先
刘明政,葛萍萍, 张雁翔, 姚俊夫,王念先
(1.武汉科技大学 机械自动化学院,武汉 430081;2.冶金装备及其控制教育部重点实验室,武汉 430081;3.韶关液压件厂有限公司,广东 韶关 512000)
主动磁悬浮轴承是一种通过可控电磁力使转子稳定悬浮的轴承,具有无接触、无润滑、无磨损、转速高和动态特性可调等优点,应用越来越广泛[1]。在高转速下转子不平衡会对系统产生较大破坏,是系统故障的主要因素。当磁悬浮转子系统在复杂工况下工作时,磁性材料相对磁导率变化明显,磁悬浮轴承非线性支承特性显著增加,转子不平衡对系统的影响更复杂,需要进行研究。
磁悬浮轴承非线性支承特性主要由系统漏磁、磁饱和等因素造成[2]。在漏磁方面:文献[3]考虑气隙漏磁,提出了一种新型永磁偏置轴向混合磁悬浮轴承,使其具有较低的功率损耗与良好的控制性能;文献[4]针对新型径向混合磁悬浮轴承,利用等效磁路法建立数学模型计算漏磁系数,并通过试验和有限元法验证了模型的正确性;文献[5]基于ANSYS和试验建立混合磁悬浮轴承非线性支承力模型,提高了大气隙混合磁悬浮轴承承载力计算精度。在磁饱和方面:文献[6]建立考虑磁饱和影响的磁悬浮轴承非线性支承力模型,试验证明该模型更精确;文献[7]考虑磁饱和影响,基于磁路法建立考虑漏磁及磁饱和等因素的磁悬浮轴承非线性支承力模型,该模型在不同的气隙长度与偏心距下计算精度均较高。
在磁悬浮转子系统不平衡响应方面:文献[8]建立刚性磁悬浮转子动力学模型,分析了控制参数对转子模态的影响,得到转子涡动摆振频率随控制参数的变化规律;文献[9]对磁悬浮转子系统稳态不平衡响应进行分析,不同转速区域采用不同的磁悬浮轴承控制参数,可改善系统动态特性;文献[10]建立主动磁悬浮电主轴系统动力学模型,分析结构参数、控制参数对系统动态特性的影响,系统响应非线性特征显著,且控制参数对系统响应影响更大。
上述磁悬浮轴承支承模型大多基于常规支承力模型,缺乏基于磁悬浮轴承非线性支承特性(考虑漏磁、磁饱和等非线性因素)的磁悬浮转子系统不平衡响应分析。 鉴于此,建立非线性支承磁悬浮转子系统模型,基于有限元法建立系统动力学模型,分析运行参数和控制参数对系统不平衡响应的影响。
1 非线性支承磁悬浮转子系统模型
1.1 磁悬浮转子系统结构
磁悬浮转子系统结构如图1所示,转子主要结构参数为:长度580 mm,外径25 mm,内径15 mm,圆盘主要结构参数为:厚度27.3 mm,外径250.0 mm,内径25.0 mm,径向主动磁悬浮轴承主要参数见表1,圆盘连接在空心转轴上,转轴由两端磁悬浮轴承支承。基于有限单元法可将该系统离散成5个节点,为方便分析,做如下假设:1)仅考虑径向振动的影响;2)圆盘为刚性圆盘,可用集中质量块单元表示;3)忽略转子重力对系统的影响。

图1 磁悬浮转子系统结构简图Fig.1 Structure diagram of magnetic levitation rotor system
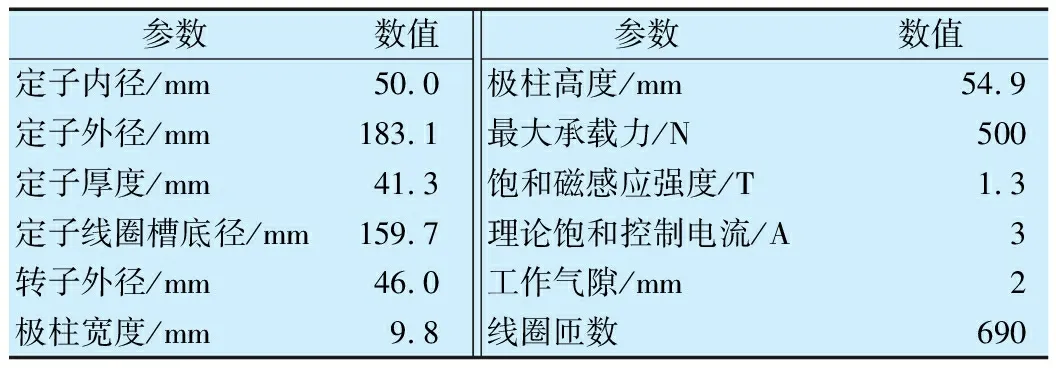
表1 径向主动磁悬浮轴承主要参数Tab.1 Main parameters of radial active magnetic bearing
1.2 磁悬浮轴承支承力模型
采用差动控制的八磁极径向磁悬浮轴承的结构及控制原理如图2所示,图中:F1,F2为线圈磁动势,Ib为偏置电流,Ix为控制电流;g0为气隙长度。
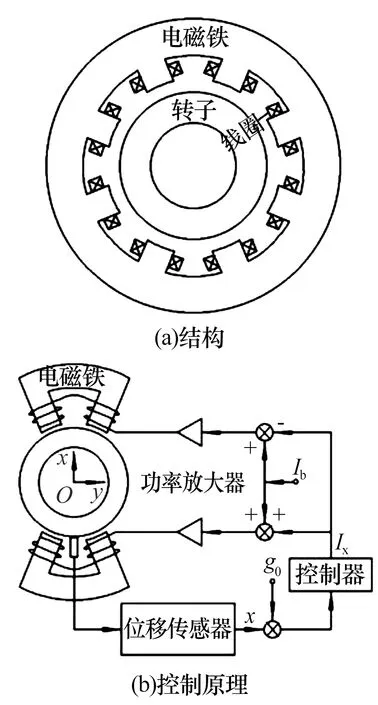
图2 八磁极径向磁悬浮轴承结构及控制原理图Fig.2 Structure and control principle diagram ofeight pole radial magnetic bearing
忽略铁磁材料的磁场耦合、涡流和磁滞的影响,为考虑漏磁及磁饱和等非线性因素的影响,可将磁场分布等效为磁路,采用场路结合法[8]划分气隙磁场、漏磁磁场,建立各磁路模型并得到总磁导或磁阻。通过幂函数拟合软磁材料磁感强度-磁场强度(B-H)曲线,确定磁饱和影响下的磁极、磁轭和转子磁阻值。气隙磁通、漏磁模型如图3所示,软磁材料B-H曲线如图4所示[8]。径向磁悬浮轴承单个磁极的等效磁路图(Equivalent magnetic circuit,EMC)如图5所示,图中:Ry,Rp,Rr分别为定子磁轭、磁极和转子磁阻,Rk为漏磁磁阻,Rg1,Rg2为磁极处气隙磁阻。
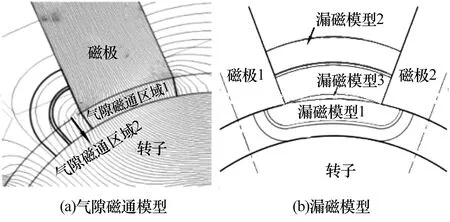
图3 磁路模型Fig.3 Magnetic circuit model
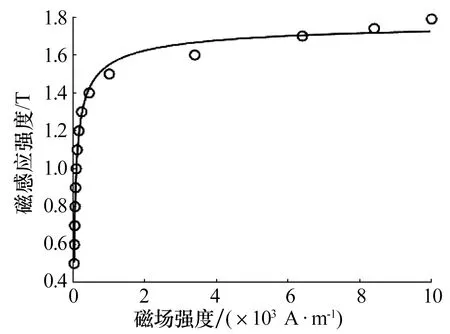
图4 软磁材料B-H曲线Fig.4 B-H curve of soft magnetic material

图5 单个磁极的等效电路图Fig.5 Equivalent circuit diagram of single magnetic pole
x方向两磁极对作用下的非线性支承力为
(1)
Φ1=
Φ3=
式中:α为磁极对夹角的一半;μ0为真空磁导率;Ap为磁极面积;Ф1,Ф3分别为两侧通过磁路气隙中的磁通;N为线圈匝数;Rg3,Rg4为磁极处气隙磁阻。
采用有限元软件验证支承力模型[5],当转子偏离平衡位置(偏移距离与气隙长度的比值为0.2),气隙长度g0=2.0 mm时,转子承载力如图6所示,负载较大时,常规支承力模型误差较大,而非线性支承力模型具有较高精度。

图6 不同负载下转子承载力曲线Fig.6 Load capacity curve of rotor under different loads
1.3 磁悬浮转子系统动力学模型
采用Euler-Bernoulli 梁单元模拟转轴,将转子离散为4个轴段单元和 5个节点,如图7所示。为考虑非线性因素对支承特性的影响,引入非线性支承力,而若将主动磁悬浮轴承单元非线性支承力作为阻尼、刚度元素处理,求解困难,在此将轴承非线性支承力当作转子所受外激励力,并施加在1#,5#节点上。

图7 磁悬浮转子系统有限元模型Fig.7 Finite element model of magnetic levitationrotor system
各刚性圆盘单元、弹性轴段单元的运动方程参考文献[11],转子的广义位移矢量为
(2)
式中:xk,yk(k=1,2,…,5)分别为节点k在x,y方向的位移;θkx,θky分别为节点k绕x,y轴的角位移。
结合转子各轴端与圆盘的运动方程,可得转子在xOz,yOz平面的运动方程为
(3)
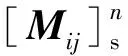
F1=(F1ax,0,0,0,udω2sin(ωt)+FL,0,0,0,F2ax,0)T,
F2=(F1ay,0,0,0,udω2cos(ωt),0,0,0,F2ay,0)T。
磁悬浮转子系统动力学方程为
(4)
在此基础上,采用Newmark-β法可得磁悬浮转子系统的不平衡响应。
2 运行参数对系统不平衡响应的影响
选取控制参数:比例系数kP=40,积分系数kI=100,微分系数kD=0.05。
2.1 负载对系统不平衡响应的影响
转子角速度ω为300 rad/s时,不同负载下磁悬浮转子系统圆盘在y方向上的不平衡响应如图8所示:1)常规磁悬浮单转子系统圆盘处的响应瀑布图仅存在转子的基频fi;2)在非线性磁悬浮转子系统中,随负载增大,系统在圆盘处的不平衡响应瀑布图中除了转子的基频之外,基频的倍频(2fi与3fi)也被激发出来,系统非线性支承特性明显。说明磁悬浮轴承非线性支承特性对磁悬浮转子系统的不平衡响应有明显影响,负载较大时,系统不平衡响应更复杂。
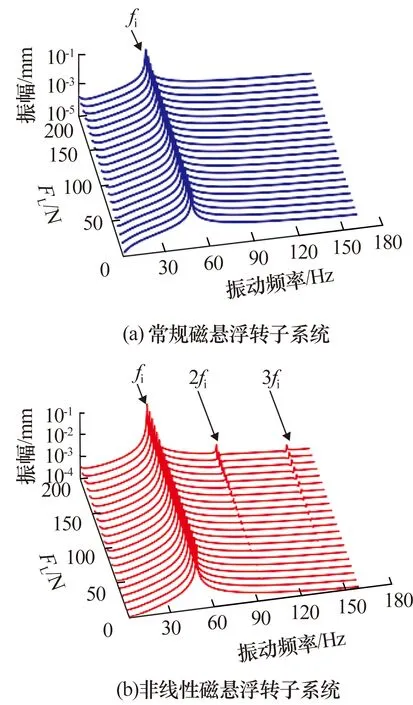
图8 不同负载下磁悬浮转子系统圆盘处的不平衡响应瀑布图Fig.8 Waterfall diagram of unbalance response at disk ofmagnetic levitation rotor system under different loads
2.2 转子角速度对系统不平衡响应的影响
负载FL为200 N时,不同转子角速度下磁悬
浮转子系统圆盘在y方向上的不平衡响应如图9所示:常规与非线性磁悬浮转子系统的不平衡响应基频与倍频规律同图8,非线性磁悬浮转子系统中倍频信号仅在某个范围内被激发,此时系统振幅增大,非线性支承特性加剧。说明转子角速度也对非线性磁悬浮转子系统的不平衡响应有影响。
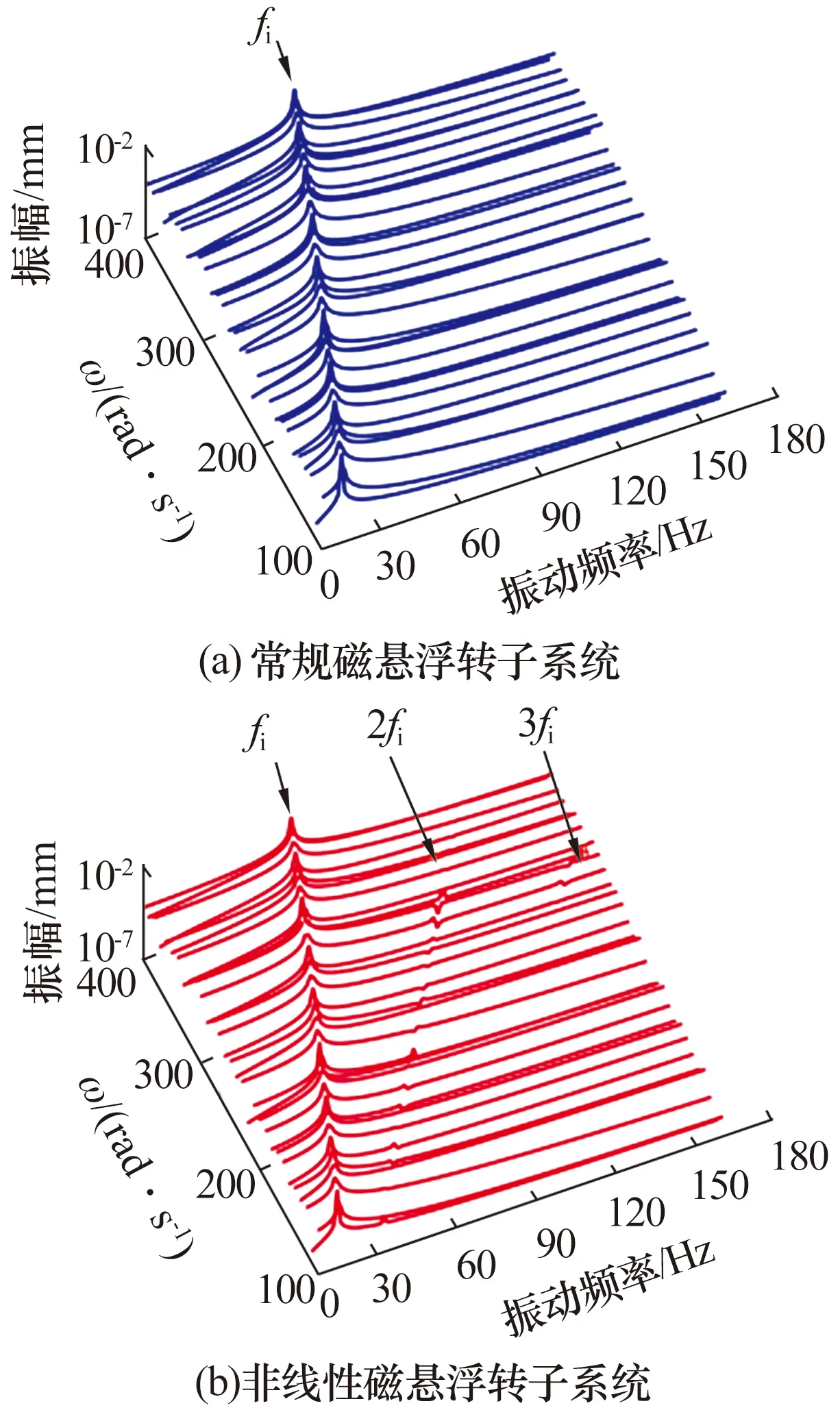
图9 不同转子角速度下磁悬浮转子系统圆盘处的不平衡响应Fig.9 Unbalance response at disk of magnetic levitationrotor system under different rotor angular velocities
不同转子角速度下磁悬浮转子系统稳定运行区域(系统所能承受最大负载区域的面积)如图10所示:1)常规和非线性磁悬浮转子系统的最大承载力随转子角速度变化而变化,说明两系统的稳定运行区域与转子角速度有关;2)在相同转子角速度范围内,非线性磁悬浮转子系统稳定运行区域明显小于常规磁悬浮转子系统,说明非线性磁悬浮转子系统稳定性较差。

图10 不同转子角速度下磁悬浮转子系统稳定运行区域Fig.10 Stable operation region of magnetic levitationrotor system under different rotor angular speeds
2.3 小结
在实际运行过程中,应尽量避免系统在较大的负载下工作,且应合理选择系统转速,以减小磁悬浮轴承非线性支承特性对系统的影响。
3 控制参数对系统不平衡响应的影响
选取运行参数FL=200 N,ω=300 rad/s。积分系数对系统响应的影响主要体现在低频段,对高频段的动态响应影响较小,此处不做分析。
3.1 比例系数对系统不平衡响应的影响
当kI为100,kD为0.05时,不同比例系数下磁悬浮转子系统圆盘在y方向上的不平衡响应如图11所示:1)常规磁悬浮转子系统只存在转子的基频fi;2)非线性磁悬浮转子系统响应中出现了转子倍频(2fi与3fi),且系统振幅随比例系数增大而增大,当kP大于40时,转子3倍频(3fi)被显著激发, 说明比例系数对非线性磁悬浮转子系统影响显著。应合理选择比例系数,避免系统产生较大的振幅,从而减小磁悬浮轴承非线性支承特性对系统不平衡响应的影响。

图11 不同比例系数下磁悬浮转子系统圆盘处的不平衡响应Fig.11 Unbalance response at disk of magnetic levitationrotor system under different proportional coefficients
不同比例系数下磁悬浮转子系统稳定运行区域如图12所示,非线性磁悬浮转子系统稳定性较差。
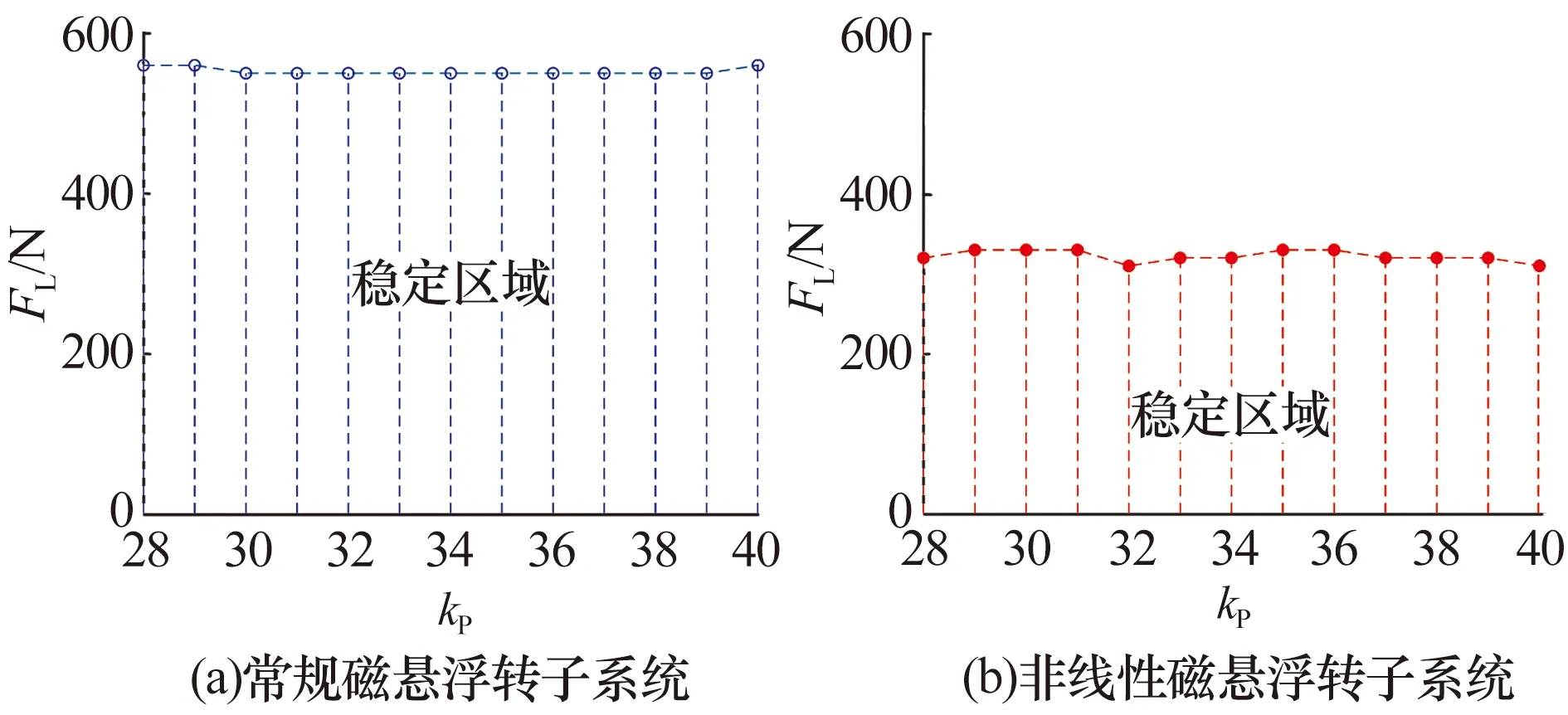
图12 不同比例系数下磁悬浮转子系统稳定运行区域Fig.12 Stable operation region of magnetic levitation rotorsystem under different proportional coefficients
3.2 微分系数对系统不平衡响应的影响
当kI为100,kP为40时,不同微分系数下磁悬浮转子系统圆盘在y方向上的不平衡响应如图13所示:1)常规磁悬浮转子系统仅存在转子的基频fi;2)当微分系数较小时,非线性磁悬浮转子系统抑制振动的能力有限,系统非线性特性明显,在系统的响应瀑布图中出现了转子倍频(2fi与3fi),随微分系数增大,系统抑制振动的能力增强,系统非线性特性减弱,响应中2fi与3fi幅值逐渐减小,当微分系数大于0.5时,3fi接近消失。说明微分系数对非线性磁悬浮转子系统的不平衡响应有明显影响,较大的微分系数能有效减小磁悬浮轴承非线性支承特性对系统不平衡响应的影响。
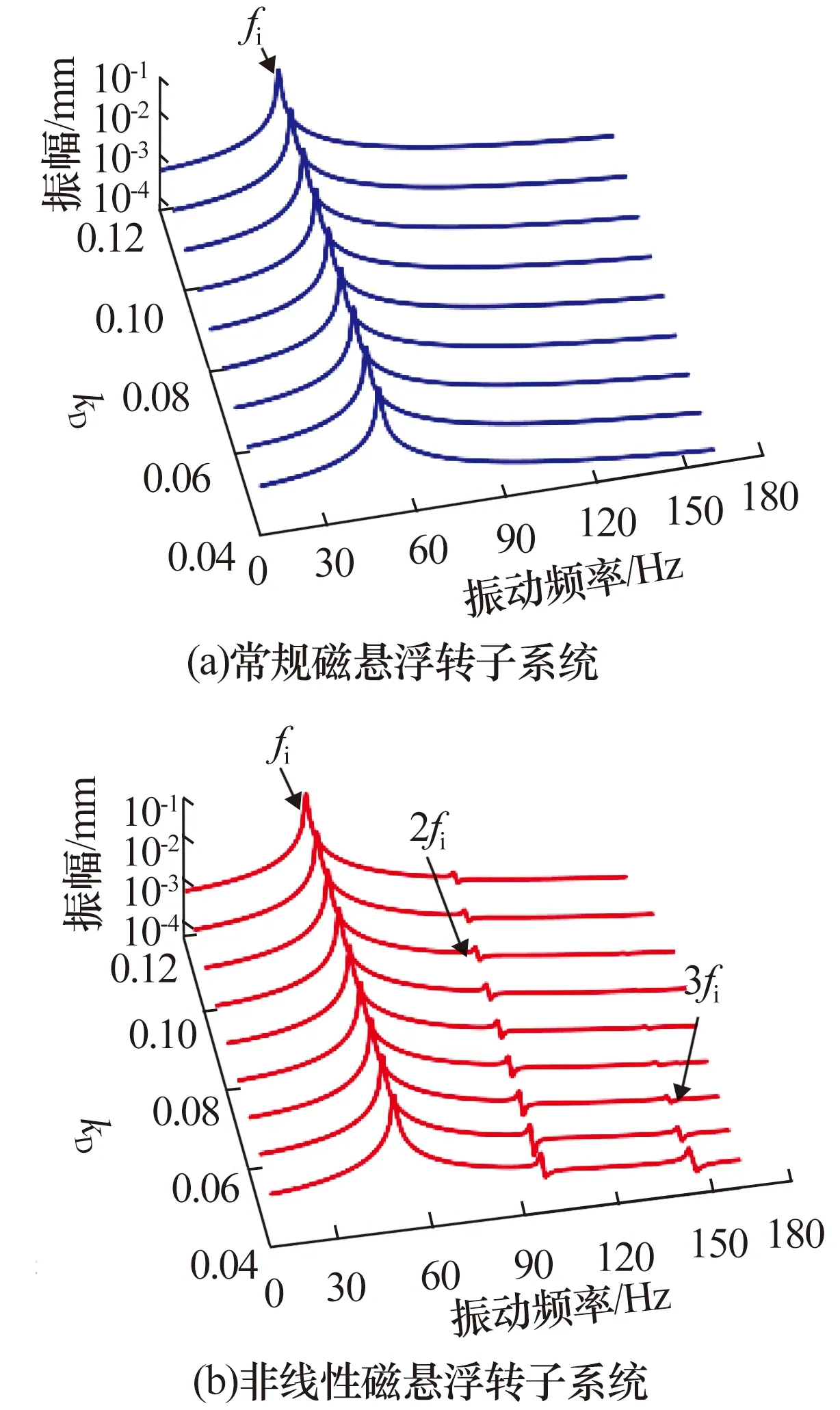
图13 不同微分系数下磁悬浮转子系统圆盘处的不平衡响应Fig.13 Unbalance response at disk of magnetic levitationrotor system under different differential coefficients
不同微分系数下磁悬浮转子系统稳定运行区域如图14所示,非线性磁悬浮转子系统稳定性较差。
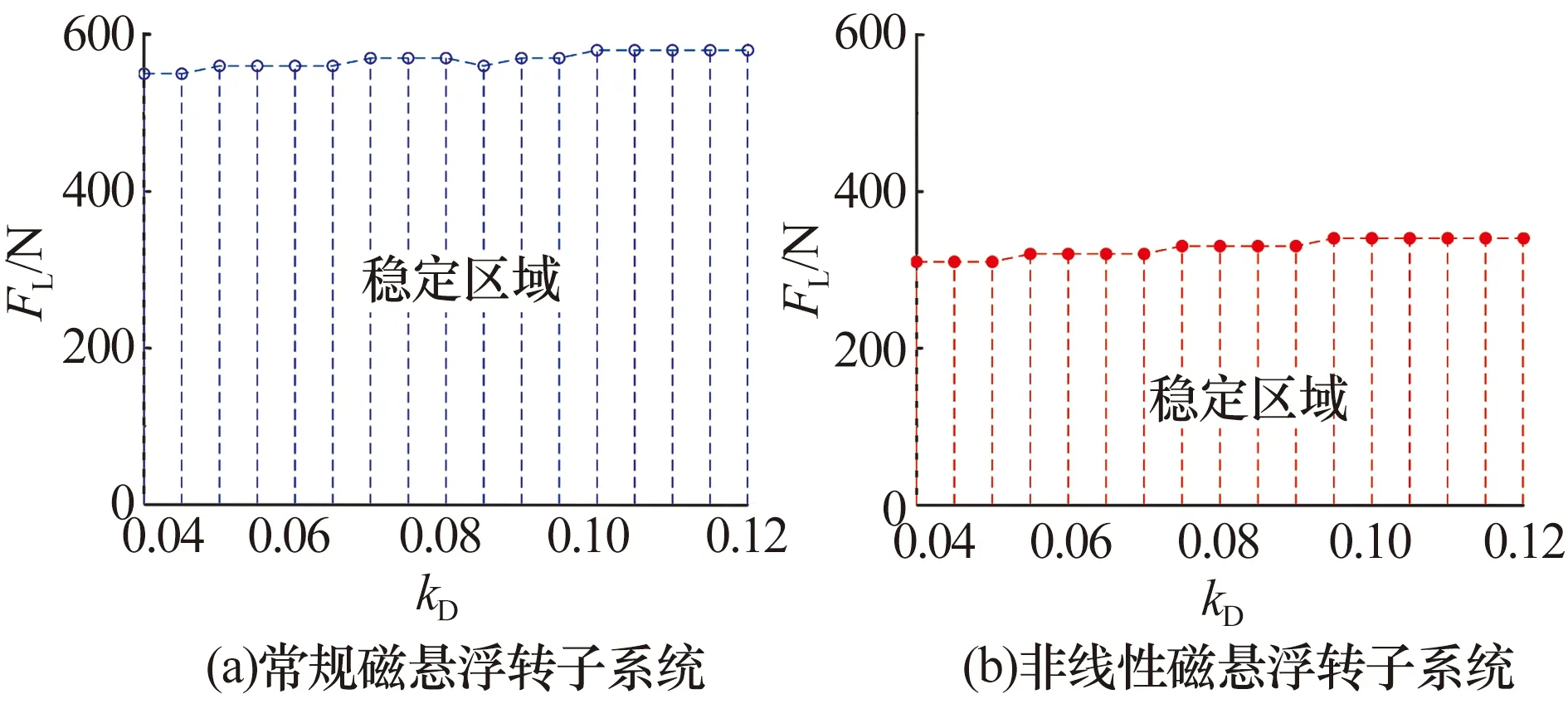
图14 不同微分系数下磁悬浮转子系统稳定运行区域Fig.14 Stable operation region of magnetic levitation rotorsystem under different differential coefficients
4 结论
建立非线性磁悬浮转子系统动力学模型,分析了运行参数和控制参数对系统不平衡响应的影响,得出以下结论:
1)考虑非线性支承特性时,较大的负载会使系统的不平衡响应中出现转子基频的倍频,响应复杂。
2)与常规系统相比,相同转速范围内考虑非线性支承特性时系统更易失稳。
3)考虑非线性支承特性时,比例系数较大和微分系数较小会使系统振幅增大,激发的转子倍频显著。选取合适的比例系数与微分系数可有效减小磁悬浮轴承非线性支承特性对系统不平衡响应的影响。
