磁悬浮无模型自适应控制参数方法的研究

蔡忠侯，钟志贤，李先瑄，祁雁英，段一戬

(桂林理工大学 机械与控制工程学院，广西 桂林 541006)

0 引言

随着工业技术的提升，很多工业实际系统变得越来越复杂，难以建立精确的数据模型，使基于模型的现代控制理论方法陷入瓶颈。针对该问题，仅依赖受控系统的输入、输出数据，而不依赖受控过程中模型信息的数据驱动控制方法开始逐渐被关注[1-3]。其中，无模型自适应控制 (Model-Free Adaptive Control,MFAC)算法因具有适用性强，结构简单，计算负担小，易于实现和鲁棒性较强等特点，在众多的数据驱动控制方法中脱颖而出。MFAC算法主要通过引入一个伪梯度的概念，建立与受控系统等价的动态线性化数据模型进行控制器的设计和稳定性分析[4]，可以有效避免系统因未建模而产生的误差；但MFAC算法需要凭借经验人工设置合适的参数初始值[1,5-7]才能获得较好的控制性能，应用有一定的局限性。

为克服传统MFAC算法的劣势，许多学者提出了有关MFAC算法参数的整定方法：文献[8]利用MFAC算法边建模边控制的特点，提出了一种二阶泛模型，并利用基于下降梯度法的参数整定优化算法对不同性能的控制器进行参数整定，结果显示与传统MFAC算法相比，改进后算法的控制效果良好；针对单输入、单输出的离散非线性系统，文献[9]提出了一种基于虚拟参考反馈整定的改进MFAC算法，仿真结果验证了改进后MFAC算法的有效性；文献[10]利用粒子群优化算法寻找MFAC算法的最优参数解，实现了倾转翼飞机在过渡段的平稳飞行；文献[11]设计了一种基于单纯形法的方式实现了参数寻优并发现了设定参数初始值的基本规律；文献[12]通过遗传算法将紧格式无模型自适应控制的η，μ，ρ，λ参数问题转化为单个参数ρ的问题，并对步长因子ρ进行动态化取值，降低了系统稳定时出现超调的可能性；针对复杂的多输入、多输出系统，文献[13]提出了一种基于拟牛顿算法的参数整定方法，通过拟牛顿算法对前3个时刻的u(0)，u(1)，u(2)，y(0)，y(1)，y(2)值进行数据拟合，选择最优参数，并在炼油厂气体分馏装置中取得了较好的控制效果；文献[14]利用磷虾算法的全局勘探能力和粒子群算法的局部搜索能力，设计了一种混合磷虾群智能算法的MFAC算法，可以快速找出最优参数来提高系统的动态性能，通过在变风量系统的试验表明了该算法可以使受控系统平稳、高效运行。

针对以上研究成果，本文通过对比增量式PD算法与全格式无模型自适应控制 (Full-Format Dynamic Linearization Model-Free Adaptive Control, FFDL-MFAC) 算法的相似性，推导出PD算法参数与FFDL-MFAC算法参数之间的关系，确定了控制单自由度磁悬浮系统的全格式无模型自适应控制器参数，并通过仿真和试验进行了验证。

1 MFAC算法

对于一般的单输入、单输出离散非线性系统

y(k+1)=f[y(k),…，y(k-ny),u(k),…，u(k-nu)],

(1)

式中：u(k)为k时刻系统的输入；y(k)为k时刻系统的输出；ny，nu为系统伪阶数；f(…):Rny+nu+2|→R为未知的非线性函数[15]。

定义HLy,Lu(k)∈RLy,Lu为在区间[k-Lu+1,k]内的所有控制输入信号以及在区间[k-Ly+1,k]内所有输出信号组成的向量，即

HLy,Lu(k)=[y(k),…,y(k-Ly+1),u(k),…,u(k-Lu+1)],

(2)

当满足k≤0时，HLy,Lu(k)=0Ly,Lu，Ly，Lu称为系统的伪阶数，0≤Ly≤ny,0≤Lu≤nu。

记

ΔHLy,Lu(k)=HLy,Lu(k)-HLy,Lu(k-1)。

(3)

针对(1)式所示的非线性系统提出2个假设: 1)除有限的时刻点外，f(…)关于各个变量的偏导数是连续的；2)除有限的时刻点外， (1)式满足广义利普希茨条件，即任意的k1≠k2,k1,k2≥0，且HLy,Lu(k1)≠HLy,Lu(k2)，有

|y(k1+1)-y(k2+1)|≤b‖HLy,Lu(k1)-HLy,Lu(k2)‖,

(4)

y(kj+1)=f[y(kj),…,y(kj-ny),u(kj),…,u(kj-nu)];j=1,2,

式中：b是一个大于0的常数。

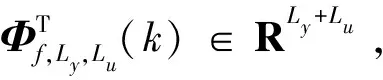
(5)

伪梯度向量为

Φf,Ly,Lu(k)=[Φ1(k),…,ΦLy(k),ΦLy+1(k),…,ΦLy+Lu(k)]T,

(6)

其是未知但有界的。

根据拉格朗日乘数法，采用以下函数作为控制输入准则函数，即

J(u(k))=|y*(k+1)-y(k+1)|2+

λ|u(k)-u(k-1)|2,

(7)

式中：λ为权重因子，用来控制输入量变化，λ>0；y*(k+1)为期望的输出信号，y*(k+1)-y(k+1)确保系统的输出与期望输出一致。

将(5)式代入(7)式中对u(k)求导并令其等于零，通过矩阵求逆原理可得到控制算法为

Δu(k)=

i=1,2,…。

(8)

为完成(8)式控制算法，需知伪梯度(Pseudo Gradient, PG)的值。对于一般的离散非线性系统，伪梯度是一个时变参数，很难确定其真实值，需要根据输入、输出数据对其进行估计，因此采用PG估计准则函数进行伪梯度的估计运算，即

J(Φf,Ly,Lu(k))=|y(k)-y(k-1)-

(9)

式中：μ为权重因子，μ>0。

由于该准则函数中只考虑了第k个采样时刻，由此准则函数推导出来的参数估计算法具有对时变参数的跟踪能力。采用与(8)式相同的求解方法，可得到伪梯度的估计算法，即

ΔH(k-1)]，

(10)

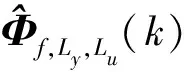
2 PD型FFDL-MFAC算法控制器

FFDL-MFAC算法是针对一类离散时间非线性提出的一种控制算法，为保证离散参数的相似性，本文采用增量式PD控制器进行无模型自适应控制器参数的初始化。

增量式PD控制算法结构为

(11)

式中：KP为比例系数；TD为微分时间常数；T为时间常数；e(k)为偏差。

在Ly=2，Lu=1的控制系统中，通过第1节求得的估计算法，可知FFDL-MFAC算法方案为

(12)

u(k)=u(k-1)+

(13)

当期望输出值y*(k)是一个常数时，(13)式可以转化为

ρ1Φ1(k)]-[-ρ1Φ1(k)+ρ2Φ2(k)]e(k+1)-

ρ2Φ2(k)e(k-2)},

(14)

其中

e(k)=y*(k)-y(k)。

(15)

对比 (11),(14)式可知

(16)

根据(16)式，首先利用相应的参数整定方法得到PD控制器的参数值，然后选定初始值λ，Ф1(1)，Ф2(1)，Ф3(1)，根据与全格式无模型自适应控制器的对应关系，可得到计算u(k)的步长因子ρ1，ρ2，ρ3。

3 FFDL-MFAC算法的应用

3.1 单自由度磁悬浮系统

磁悬浮系统是一个复杂的非线性系统[15]，其数学模型难以精确建立，使控制器的选择受到限制，而FFDL-MFAC算法仅需要在线的I/O数据，避免了建立数学模型造成的误差，将其应用于磁悬浮系统具有很大的研究意义。

以文献[16]提出的复杂非线性单自由度磁悬浮系统作为模型，单自由度磁悬浮系统的结构如图1所示。

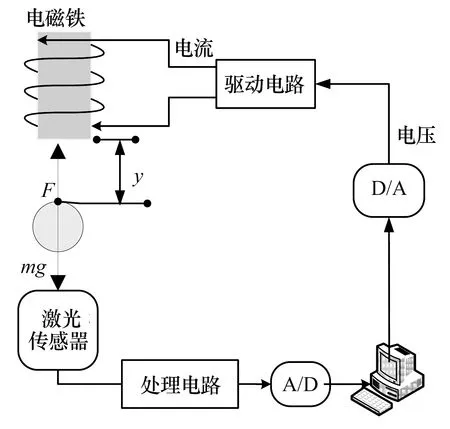
图1 单自由度磁悬浮系统结构图

经过平衡点处的线性化处理后，得到单自由度磁悬浮系统的传递函数为

(17)

式中：Ka为功率放大器系数；i0为电磁铁中平衡电流；x0为被控对象的平衡位移；s为控制系统中关于时间的微分算子；g为重力加速度。

针对本文研究的磁悬浮小球系统，小球的质量为m=94 g，Ka=6.508，i0=0.394 3 A，x0=0.01 m。则单自由度磁悬浮小球系统的开环传递函数为

(18)

确定采样时间T=0.001 s，将(18)式经离散化处理后可知该单自由度磁悬浮系统的动态数学模型为

y(k+1)=2.002y(k)+y(k-1)+3.819×10-6u(k)+3.819×10-6u(k-1)。

(19)

3.2 仿真结果

通过传统的整定方法确定增量式PD算法的参数值，并根据(16)式计算FFDL-MFAC算法的参数值(表1)。

表1 2种算法仿真参数取值Tab.1 Simulation parameter values of two algorithms

为验证PD型全格式无模型自适应控制器的有效性，通过MATLAB/Simulink建立单自由度磁悬浮系统仿真模型并进行分析。仿真试验框图如图2所示，确定期望输出位置信号为y*(k)=1，并在t=1.5 s时加入阶跃信号作为扰动输入；步长因子ρi(i=1,2,3)发生变化时对控制器跟踪性能的变化如图3所示。仿真结果表明，步长因子ρi(i=1,2,3)都会使控制器的控制性能发生改变，变化较大时会导致系统变为不稳定状态，证明了通过PD控制算法对FFDL-MFAC控制器的步长因子进行整定的有效性。PD型全格式无模型自适应控制器与PD控制器的仿真结果对比如图4所示，结果表明这2种控制器都可以使系统稳定，且基于PD型全格式无模型自适应控制器的磁悬浮小球系统的动态响应时间更短，在加入扰动信号后可以更快地恢复到稳定状态，具有更强的鲁棒性。

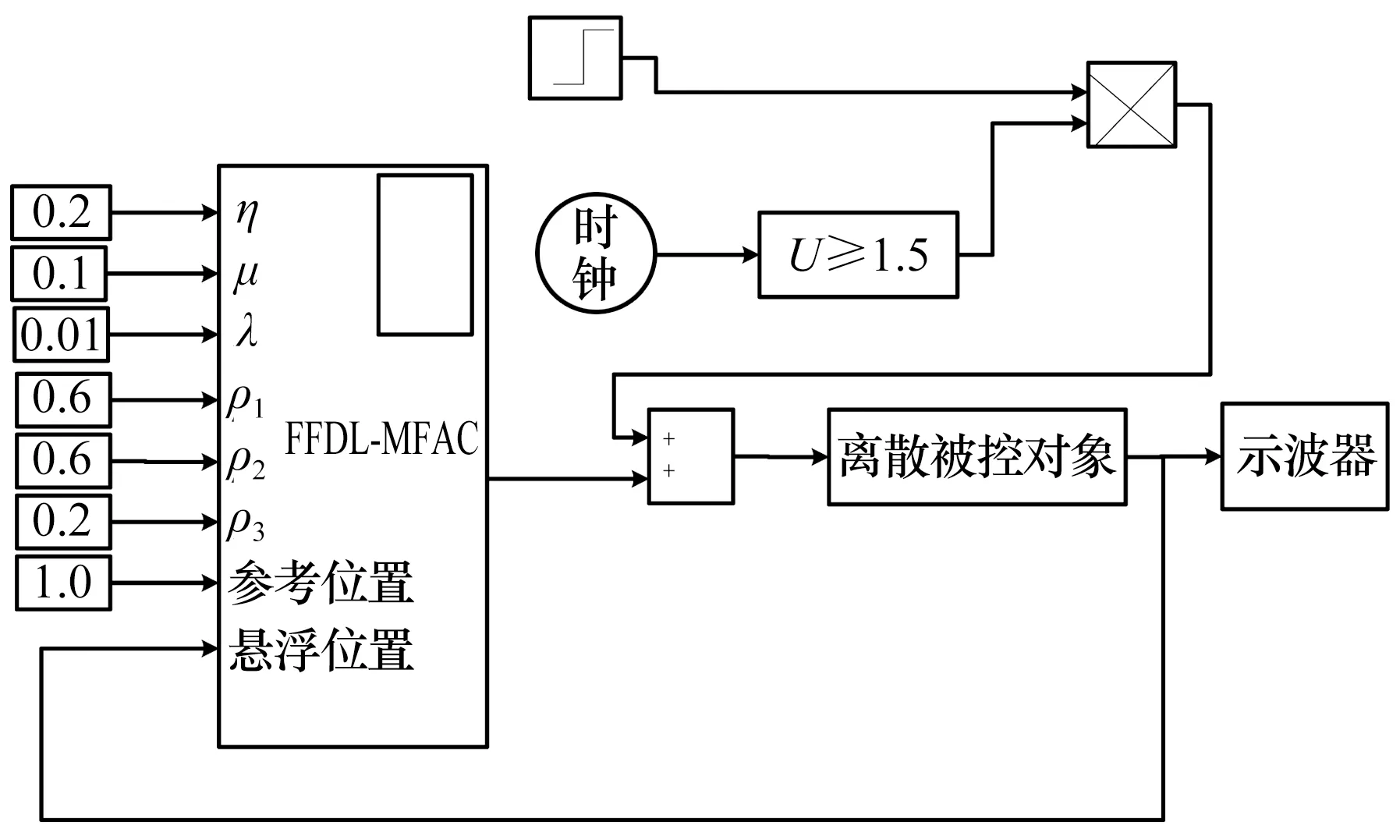
图2 单自由度磁悬浮系统仿真试验框图

图3 不同ρ控制器跟踪信号结果Fig.3 Tracking signal results of different ρ for controller

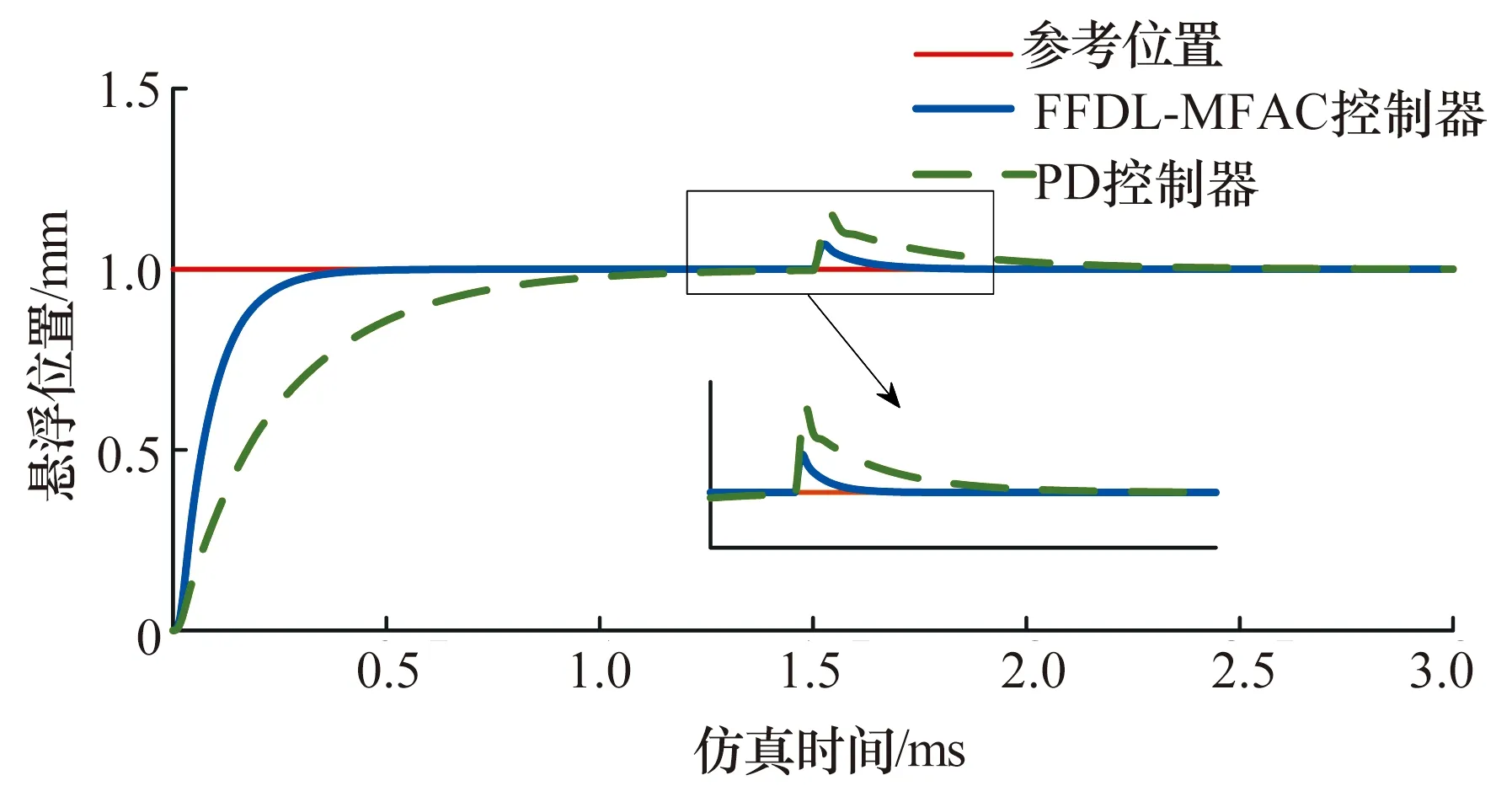
图4 2种算法仿真结果对比Fig.4 Comparison of simulation results of two algorithms

3.3 试验结果

以图5的单自由度磁悬浮试验平台为研究对象，验证PD算法整定全格式无模型自适应控制器参数方法的有效性和适用性。2种算法的实时控制参数取值见表2。通过实时控制改变小球稳定的参考位置，进一步验证FFDL-MFAC算法对磁悬浮系统的鲁棒性，试验结果如图6所示。单自由度磁悬浮系统通过PD算法整定全格式无模型自适应控制器和PD控制器的位移输出对比结果分析如图7所示， 2种控制器都可以使被控对象稳定在期望输出位置处，但是相比于PD控制器，利用PD型全格式无模型自适应控制器可以使被控对象更快、更稳地悬浮在指定参考位置，且根据表3可知该算法的误差均方根(Root Mean Square of Error，RMS)减小了0.002。

表3 2种算法的误差均方根Tab.3 RMS of two algorithms

图5 单自由度磁悬浮试验平台

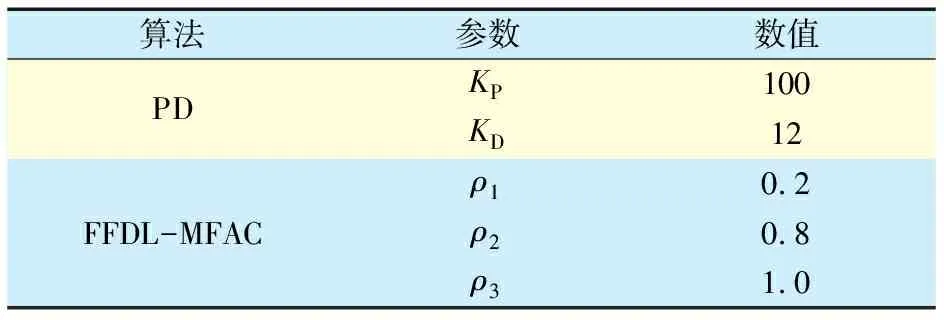
表2 2种算法实时控制参数取值Tab.2 Real-time control parameter values of two algorithms

图6 不同参考位置的实时控制结果

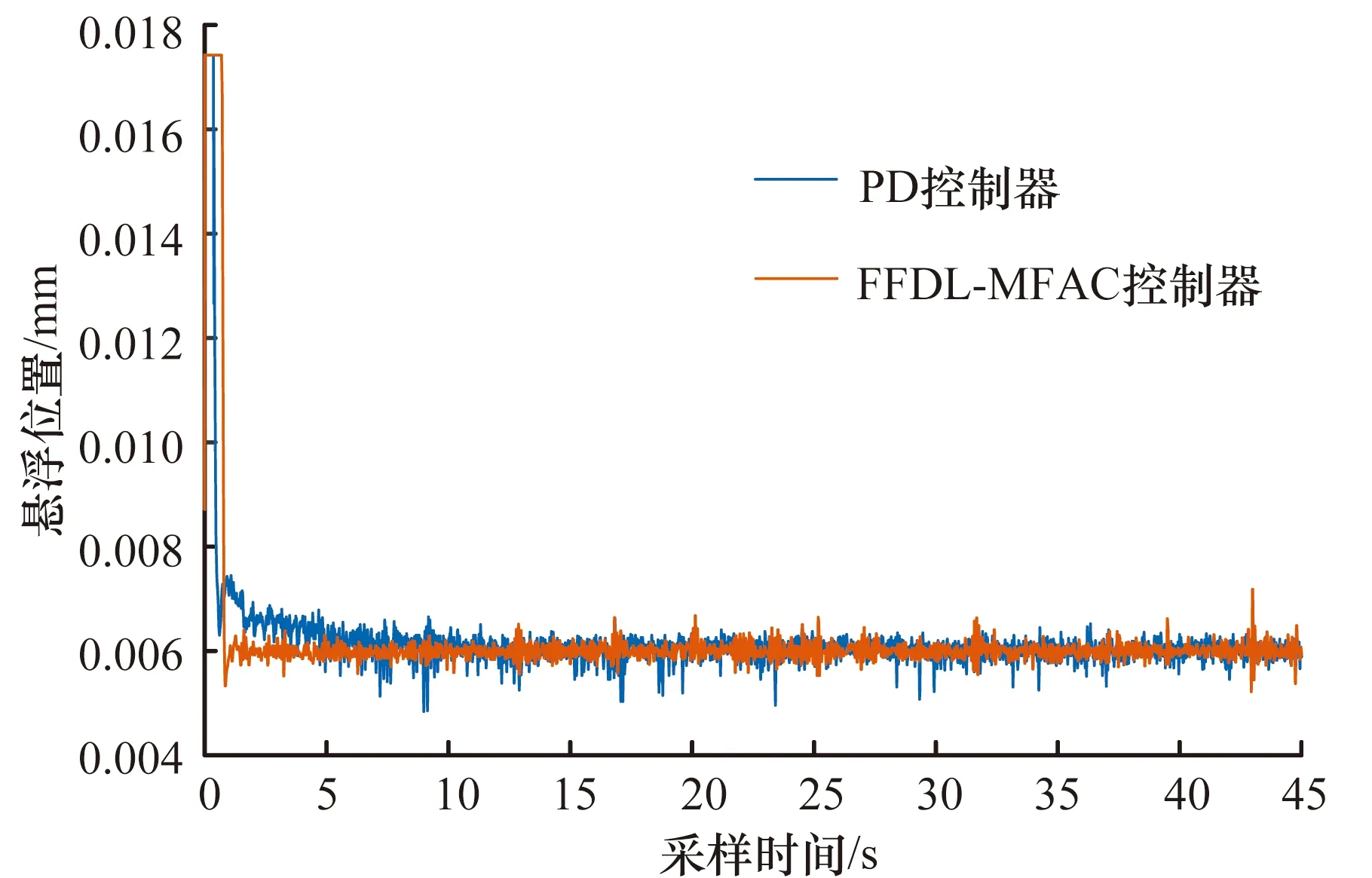
图7 2种算法的实时控制结果对比

algorithms

4 结束语

通过对比增量式PD算法与FFDL-MFAC算法的相似性，建立PD型FFDL-MFAC算法，实现FFDL-MFAC算法的参数初始化，并将该算法应用于单自由度磁悬浮系统。仿真和试验结果表明，PD型无模型自适应控制器和PD控制器都可以使磁悬浮系统稳定悬浮，基于PD型无模型自适应控制器的响应时间更短，鲁棒性更强。