天然气压差发电机用主动磁轴承-转子系统支承特性参数分析

李卓远，李栋杰，许浩德，龚亮，张钢

(上海大学 机电工程与自动化学院，上海 200444)

高速电动机作为微型燃气轮机(以下简称微燃机)的重要部件，轴承支承问题一直是限制其快速发展和工业实际应用的“瓶颈”。滚动轴承的高速转子与轴承本体直接接触，导致高速电动机运转中存在摩擦损耗大、发热严重以及可靠性低等问题，同时也直接限制了高速电动机转速的进一步提升[3]；因此，非接触轴承，特别是磁悬浮轴承(以下简称磁轴承)成为了高速电动机的首选支承。

国内外学者针对磁轴承支承特性进行了相关研究：文献[4]探究了使用液压装置并通过计算机控制轴承刚度来改变其动态性能的机理；文献[5]提出了基于有限元模型和单自由度凝聚的柔性转子电磁轴承支承刚度、阻尼参数识别方法；文献[6]探究了不同工作频率区间下可控磁轴承的支承特性并从支承特性的角度设计了PID控制器；文献[7]提出了一种同时辨识柔性轴承-转子系统中轴承参数和不平衡参数的辨识算法,建立转子系统的动力学数值求解模型并进行了验证；文献[8]开发了一种通过转子不平衡响应识别同步轴承支承参数的程序，该程序记录了1 500～3 500 r/min 转速范围内的力参数以及轴承-转子系统的一阶弯曲临界转速，并通过试验验证了其正确性；文献[9]设计了一套基于LabVIEW的电磁轴承刚度、阻尼测试系统。综上可知，磁轴承支承参数的辨识可以验证轴承-转子系统是否跨过一阶弯曲临界转速，对系统的稳定性设计有重要意义。

本文基于某型微燃机天然气压差发电机的设计参数给出主动磁轴承支承方案，通过转子动力学理论分析轴承-转子系统的动力学模型，探究主动磁轴承的刚度、阻尼求解方法，并利用ANSYS-Workbench求解轴承-转子系统的固有频率和振型，以确保转子系统安全运行。

1 主动磁轴承-转子系统结构设计

1.1 主动磁轴承支承方案

某型微燃机天然气压差发电机(以下简称发电机)的转子使用磁轴承支承，发电机的额定功率为490 kW、额定转速为36 000 r/min，发电机整体运行效率不低于85%。根据发电机要求和磁轴承设计理论，微燃机支承系统设计需考虑以下因素：1)叶轮需为主轴提供较大扭矩以带动主轴旋转，故采用永磁同步发电机直接驱动转轴；2)发电机转子安装在2套径向磁轴承的内侧，为保证发电机可提供足够的扭矩以满足较大负载，与发电机转子配合的转轴轴段的轴径应较大；3)轴顶端安装叶轮，气压差会产生一定的轴向力，该轴向力完全由轴向磁轴承承受，因此轴向磁轴承也需要较大尺寸；4)为解决轴向磁轴承推力盘尺寸过大导致推力盘质量太大的问题，将轴向磁轴承的磁回路进行弯曲，推力盘做成内凹状且径向转子、推力盘、测量环之间用轴套隔开，避免磁轴承之间的磁干扰；5)由于转子系统悬空旋转且转子部件质量较大，发电机和轴承的定子与转子间的气隙值均较小，轴端两侧安装有超高速陶瓷球角接触球轴承XC71909作为辅助支承(也称保护轴承)，在磁轴承失效时能够支承转子直至恢复正常运行或降到安全速度。综合考虑以上因素，最终确定的发电机磁轴承支承系统如图1所示。

1.2 磁轴承的结构参数

磁轴承结构优化设计的实质是根据承载要求和使用条件来协调线圈腔的横截面积和磁铁的磁极面积。

在径向磁轴承的定子中，由于绝缘材料要占一定的体积，绕线方式也会留下一定的空隙，定子线圈腔并不全是有效载流面积，因此有

N=λJAcui,

(1)

式中：N为单个磁极线圈匝数；λ为占空系数；J为电流密度；Acui为线圈腔面积。

1—角接触球轴承；2—轴向磁轴承定子；3—推力盘；4—位移传感器；5—径向磁轴承定子；6—径向磁轴承转子；7—发电机转子。

定子每极磁极面积Ai和线圈腔面积Acui的大小与磁极数Np有关，当径向磁轴承的内径D1、磁极高度h和轴向长度l一定时，磁轴承的定子体积为常数K1，即

(2)

当径向磁轴承的线圈导线、铁磁材料和定子与转子间的初始气隙值C0确定后，设常数K0为

(3)

式中：μ0为真空磁导率。

磁轴承为非线性的铁磁性材料，其具有磁饱和特性，因此线圈腔面积存在一个上限K2，则

(4)

式中：Bs为铁磁性材料的磁饱和密度。

根据电磁力计算公式可知，多磁极径向磁轴承在竖直方向上的电磁合力Fy为

(5)

则

(6)

对(6)式中的磁极数Np求导可得

(7)

由(7)式可知，在其他参数不变的情况下，径向磁轴承在y方向上的最大电磁合力随着磁极数Np的增大而减小。本文径向磁轴承选择8对磁极结构，即磁轴承的磁极数Np=16。在定子内径一定的情况下，磁极越多则轴承定子的磁极宽度t越小，为了降低耦合度，将2个同极磁极合并为一个进行结构优化，优化后磁极数为12个。

根据磁通密度公式，当定子的线圈绕组电流达到最大值时，工作时电磁激励的磁场强度达到最大值Bmax，能发挥出硅钢片的最大电磁性能。线圈绕组中的最大电流值Imax由功率放大器提供的最大电流确定，偏置电流一般为I0=0.5Imax，则线圈安匝数N为

(8)

静态偏置工作状态下，设气隙中的磁感应强度为B0，则构成完整磁回路的一对磁极线圈总匝数Ntotal为

(9)

当转子处于平衡偏置状态时，根据选定的偏置电流I0，可求出绕组铜线的最小线径d,即

(10)

电流密度J的一般取值范围为2～5 A/mm2，本文取3 A/mm2。

以上分析主要是分配磁铁和铜线体积所占的比例，定、转子长度等其他结构参数皆为单独设计，达到承载要求即可。本文采用的发电机转子外径为96 mm，内径为48 mm，转子保护套厚度为3 mm，转子铁芯长度为400 mm，铜导线线径1.22 mm。

与径向磁轴承的定、转子结构相比，传统轴向磁轴承的结构较为简单，且二者计算方法基本相同，故不再赘述。径、轴向磁轴承结构参数见表1。

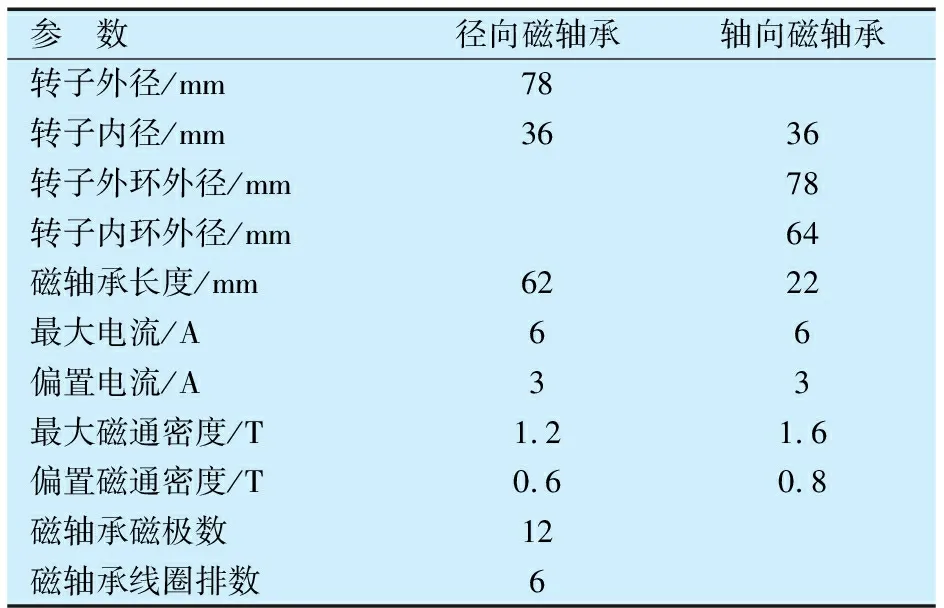
表1 径、轴向磁轴承结构参数

2 主动磁轴承-转子系统支承特性参数求解

2.1 转子系统坐标系

刚度和阻尼[10]是轴承-转子系统振动分析的重要支承特性参数，主动磁轴承的支承刚度和阻尼特性对于转子系统的工作精度和振动特性有极为显著的影响。

主动磁轴承支承系统由2套径向磁轴承和1套轴向磁轴承组成，以约束轴承-转子系统能够正常悬浮所需的5个自由度，即质心在x，y，z方向的平动和绕x轴、y轴的转动。图2为五自由度主动磁轴承支承系统示意图。

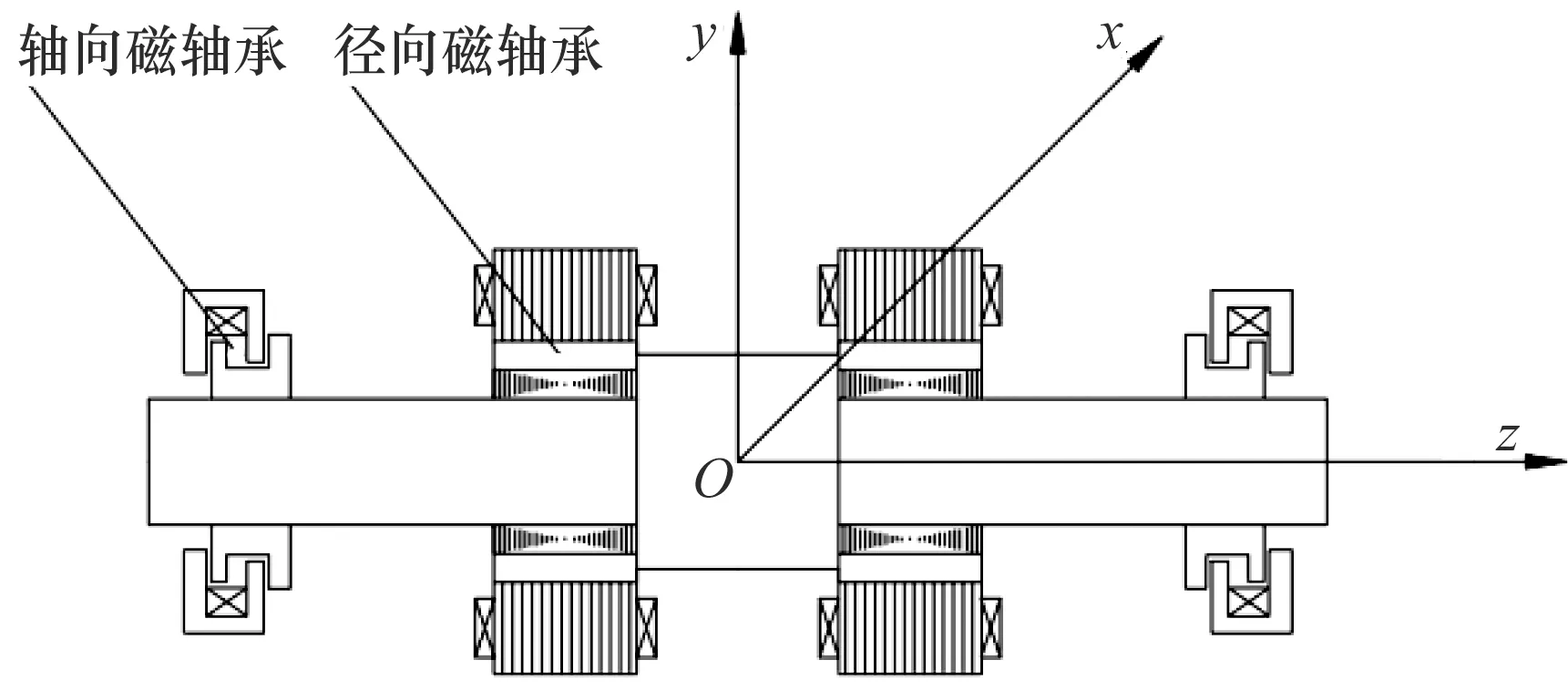
图2 五自由度主动磁轴承支承系统示意图Fig.2 Diagram of five degree of freedom active magneticbearing support system

2.2 转子系统径向支承特性求解

转子系统在径向存在xOz和yOz平面的运动且相互之间存在耦合作用。由于转子系统在这2个平面的运动完全相似，以yOz平面的运动为例对转子系统径向支承特性进行求解。

假设转子系统存在一个沿y轴方向上的位移Δy，由于本文磁轴承采用大、小磁极的结构形式，传统的磁极电磁合力数学模型已不适用，故结合麦克斯韦电磁力计算公式将电磁合力公式变形为

ΔFy=F1-F2=

(11)

式中：F1为上磁极与转子间的电磁吸力；F2为下磁极与转子间的电磁吸力；(I0+iy)为上磁极电流变化；(I0-iy)为下磁极电流变化；C0为径向转子与径向磁轴承同心时的半径间隙；N1，N2分别为大、小磁极线圈匝数；A1，A2分别为大、小磁极面积；αi为磁极与竖直方向夹角，i=1,2,3。具体原理如图3所示。

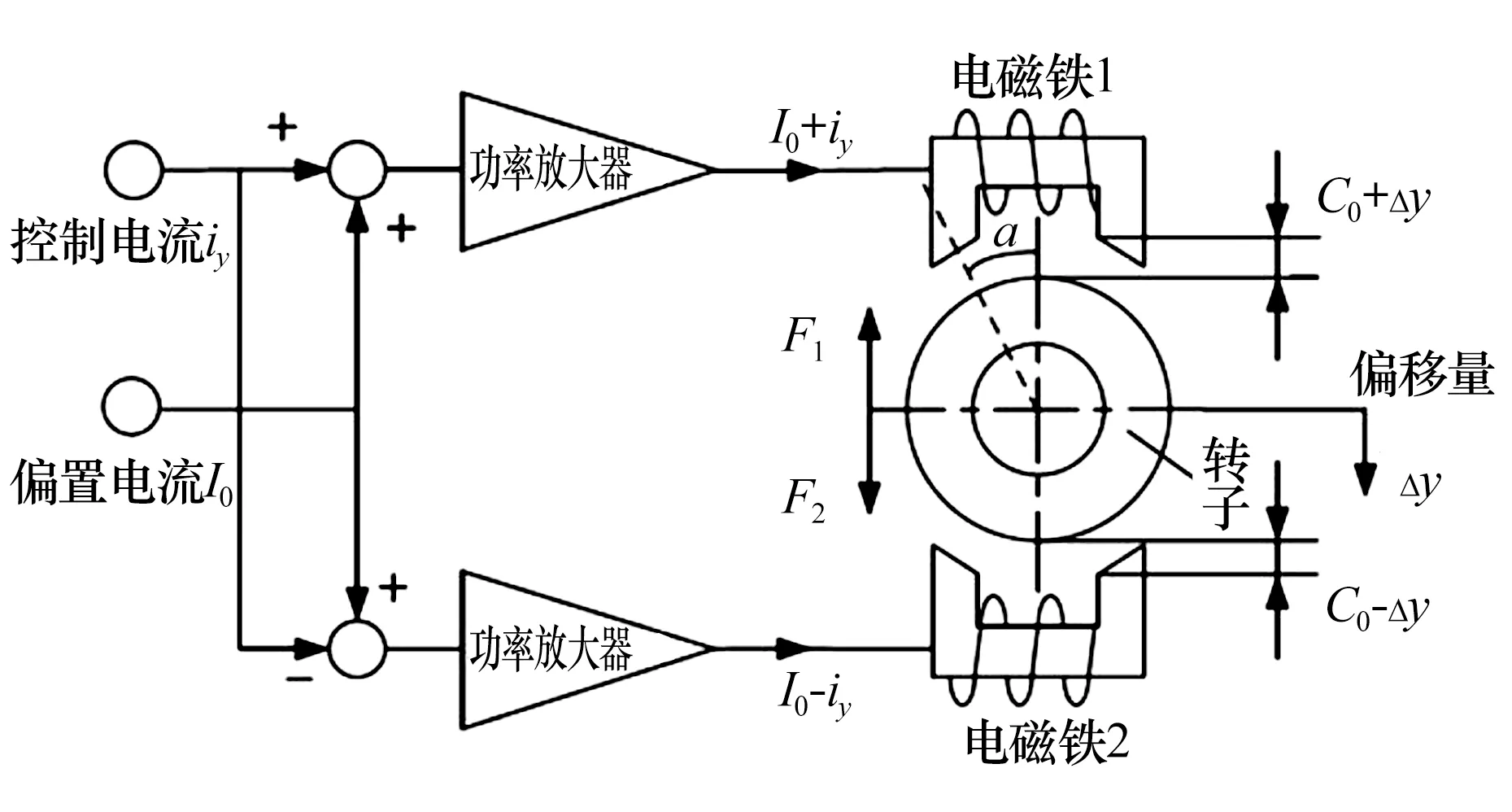
图3 差动控制支承原理Fig.3 Schematic diagram of differential control support

当转子在平衡点附近工作时，将电磁力用泰勒级数在平衡点(iy=0,Δy=0)处展开可得

(12)

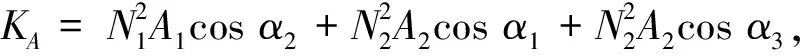
(13)

Rny为三阶以上的高阶小量，需要略去。将(12)式整理后可得y方向上的电磁力fy(i,y)为

fy(i,y)=-kyi0i+kyy0y，

(14)

式中：kyi0为y方向上的电流刚度系数；kyy0为y方向上的位移刚度系数；Cy0为转子铁心与定子铁心平衡位置时y方向的气隙。

以y方向为例，推导轴承径向等效刚度和阻尼。在不考虑铁心材料磁阻时对 (14) 式进行变换可得y方向转子的力学方程，即

(15)

式中：Fy为作用于转子(y方向上对应于一个轴承)的外干扰力。

对(15)式进行拉普拉斯变换可得

ms2Y(s)=kyy0Y(s)-kyi0Iy(s)+Fy(s)。

(16)

本文使用PID控制策略，设整个系统传递函数为G(s)，根据磁轴承的工作原理可知，位移传感器将位移信号转化为控制电流的电信号，经过功率放大器放大之后传递给磁轴承系统，有Y(s)G(s)=Iy(s)，将其代入(16)式并将s换为jω可得

[-mω2-kyy0+kyi0Re(G(jω))]Y(jω)+

jkyi0Im(G(jω))Y(jω)=Fy(jω)。

(17)

转子系统的单自由度振动方程为

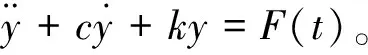
(18)

对(18)式进行拉普拉斯变换可得

(-mω2+k)Y(jω)+jωcY(jω)=F(jω)。

(19)

对比(17)与(19) 式可得PID控制的转子系统的等效刚度项为-kyy0+kyi0Re(G(jω))，等效阻尼项为kyi0Im(G(jω))/ω。同理可得x方向的刚度和阻尼。

则径向磁轴承的等效刚度k和等效阻尼c为

kxx=-kxx0+kxi0Re(G(jω))，

(20)

kyy=-kyy0+kyi0Re(G(jω)),

(21)

(22)

(23)

将支承特性参数(表2)数据代入上述公式可求得转子系统径向等效刚度和等效阻尼kxx= 62 642.222 N/mm，kyy=846.743 N/mm，cxx=8 367.694 N·s/m，cyy=182.575 N·s/m。

表2 支承特性参数Tab.2 Support characteristic parameters

2.3 转子系统轴向支承特性求解

对于轴向推力磁轴承，在不考虑推力盘发生倾斜的情况下，设轴向磁轴承定子与转子的初始气隙为Cz0，推力盘在轴向定子电磁力作用下所受的力为

(24)

则零点位置(z=0，iz=0)轴向的位移刚度系数和电流刚度系数分别为

(25)

(26)

与求解转子系统径向等效刚度和阻尼类似，可得轴向磁轴承对转子系统的等效刚度和等效阻尼为

kzz=-kzz0+kzi0Re(G(jω)),

(27)

(28)

将表2支承特性参数代入上述公式可求得转子系统轴向等效刚度和阻尼为：kzz=7.5×106N/mm，czz=700 N·s/m。

3 主动磁轴承-转子系统模态仿真分析

3.1 仿真参数设置

根据上述计算结果，运用有限元分析软件ANSYS-Workbench对转子系统进行模态分析，计算转子系统在磁轴承支承下的临界转速及振型。

为了分析主轴的转子动力学特性，将Solver属性设置为Damped；在模型的connections中加入bearing与spring作为磁轴承的等效刚度与等效阻尼，并将计算出来的刚度与阻尼输入到stiffness与damping中；在求解器中设置转子模型转速，设置5个速度节点，从小到大依次为：0，100，2 000，10 000，80 000 r/min；打开陀螺效应并设置最大模态阶数为15阶，进行模态分析求解。

3.2 模态分析及临界转速求解

通过ANSYS-Workbench求解得到转子系统前6阶模态的临界转速及频率见表3。

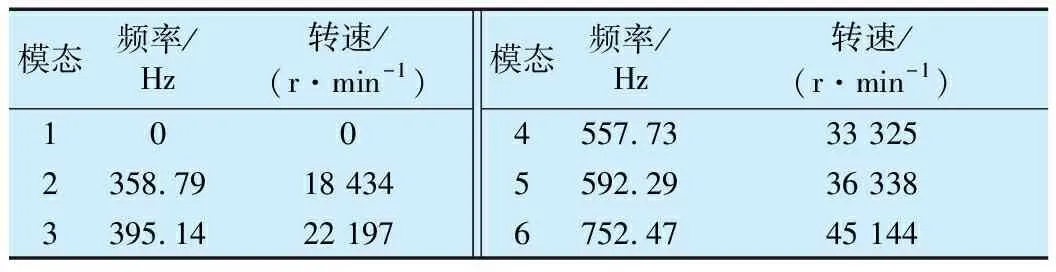
表3 转子系统前6阶模态的临界转速及频率

由表3可知第1阶模态频率是0 Hz，代表系统径向刚体振动。导出转子系统坎贝尔图(图4)，可看出转子系统的转速提升曲线与各正进动与反进动曲线的交点即为临界转速点。提取转子系统前6阶模态振型如图5所示。

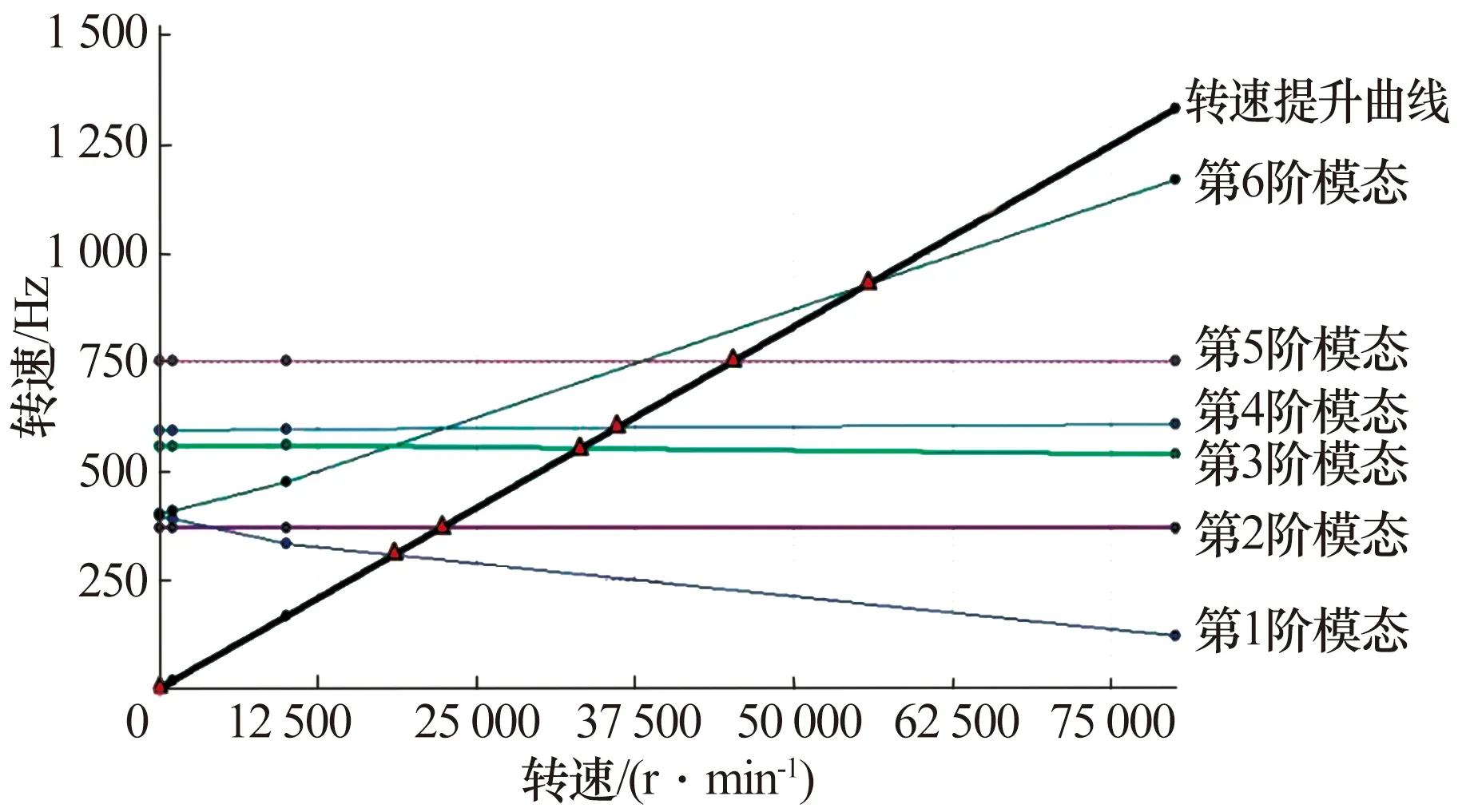
图4 转子系统坎贝尔曲线Fig.4 Campbell curve of rotor system

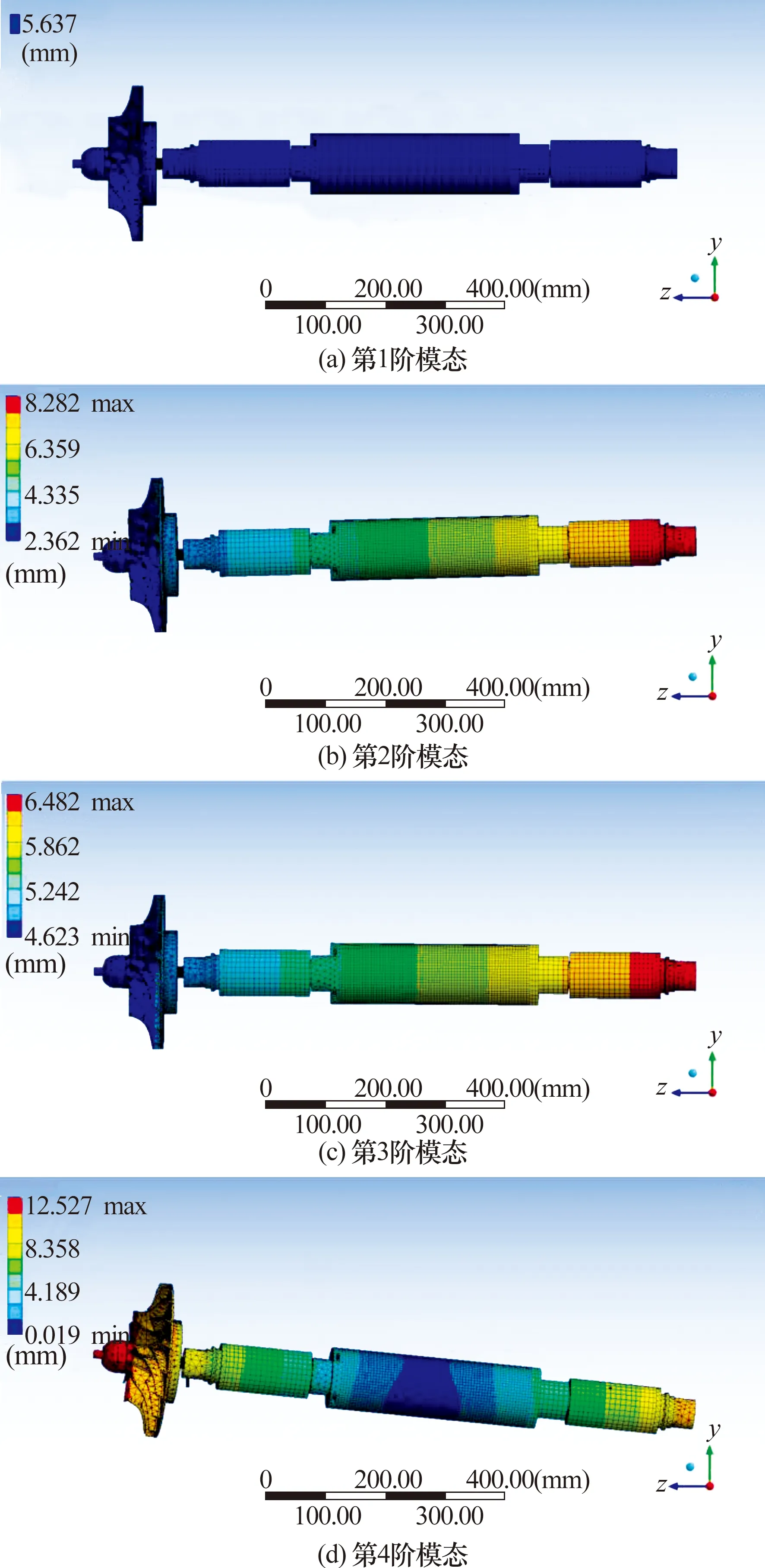
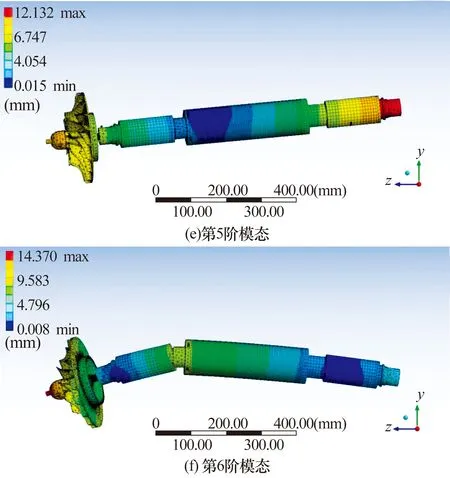
图5 转子系统前6阶模态振型Fig.5 First six vibration modes of rotor system

由图5可知转子在第6阶临界转速发生了弯曲，即第6阶为弯曲模态，也即转子系统的第6阶临界转速为转子系统的第1阶弯曲临界转速。由图5及表3可知，转子系统一阶正进动弯曲临界转速为45 144 r/min，而本文涉及的微燃机转子系统的最高转速为36 000 r/min，为一阶弯曲临界转速的79.7%。因此，转子系统的最高转速介于第5阶临界转速与第6阶临界转速之间，加上控制器的作用，转子系统可以稳定旋转。

4 结束语

根据实际工况对微燃机490 kW天然气压差发电机中的磁轴承支承部分进行结构设计，并给出物理参数；结合磁轴承的结构参数以及控制系统的相关理论求解转子系统径、轴向支承参数；建立转子系统三维模型并求解其固有频率和振型，结合坎贝尔图确定转子系统的临界转速，并确认转子系统在工作转速范围内处于安全状态。对磁轴承在微燃机领域的工业应用有一定指导作用。