主动磁悬浮轴承-储能飞轮转子系统振动主动控制

高峻泽，柳亦兵，周传迪，张彬

(1.华北电力大学 先进飞轮储能技术研究中心，北京 102206；2.贝肯新能源天津有限公司，天津 300300)

主动磁悬浮轴承(Active Magnetic Bearing，AMB)具有无机械接触，零磨损失效，低待机功耗，长使用寿命，低维护成本和可主动控制等优势，广泛应用于飞轮储能领域[1]。随着飞轮储能对电网调峰、调频的逐步应用，飞轮转子趋向于高速化以及宽转速范围的工作特点，导致飞轮转子系统面临多次过临界转速问题。由于飞轮转子存在材料缺陷、加工精度、工作变形等因素造成的不平衡质量，在过临界转速时可能产生较大振动，对转子运行可靠性产生不利影响，故需对飞轮转子在高速旋转状态下的不平衡振动进行有效控制[2]。

通过AMB实现转子系统不平衡振动控制主要分为两类方法[3-4]：1)自动平衡方法(最小作用力补偿控制)，其原理为在传感器采集的位移信号进入控制器前，通过引入位移补偿信号或滤波方法，消除与转速同频的不平衡振动信号分量，不对该分量产生控制力，使转子绕其惯性主轴旋转，自动平衡方法主要有自适应陷波器法[5-6]、自适应最小均方误差(Least Mean Square，LMS)算法[7-9]和迭代搜索法[10]等；2)不平衡补偿方法(最小位移补偿控制)，其实质为通过一定控制算法使AMB产生一个与转子自身不平衡力大小相等、方向相反的补偿力，从而使转子绕其几何中心旋转，不平衡补偿方法主要有自适应自对中方法[11]、基于模型的补偿方法[12]、基于观测器的补偿方法[13]、影响系数法[14]等。以往文献中大多针对AMB刚性转子的某一固定转速或某一小范围转速段设计相应的控制算法，对宽转速范围内实现不平衡振动控制的研究较少。此外，文献[15]首次表明在AMB-储能飞轮转子系统中，除残余不平衡激振力产生与转速同频的简谐振动外，还存在因系统固有频率而产生的自由振动，该文献采用变控制器参数的方法在一定程度上减弱了2种振动频率接近时系统产生的“拍振”现象，但影响依然很大。

针对AMB-储能飞轮转子系统全转速范围内的振动问题，在自适应LMS算法的基础上，提出了一种自适应变步长LMS算法，可同时解决由不平衡产生的同步转速不平衡振动和由临界转速产生的“拍振”现象。首先，基于有限单元法建立了AMB-储能飞轮转子系统模型；然后，在已有步长因子的基础上提出了一种新的步长因子迭代公式；最后，对提出的自适应变步长LMS算法的有效性进行了验证。

1 AMB-储能飞轮转子系统动力学建模

AMB-储能飞轮转子系统的立式结构如图1所示，飞轮转子轴向由永磁轴承支承，径向由上下2套主动磁悬浮轴承支承。

为便于分析，特作以下假设：转子是轴对称的，忽略轴向永磁轴承对径向的干扰力，传感器与AMB在轴向位置上重合。

根据转子动力学理论，基于有限单元法得到AMB-储能飞轮转子系统的动力学方程为

(1)

式中：xk，yk(k=1,…,n)分别为飞轮转子n个节点沿x，y方向的位移；αk，βk分别为飞轮转子n个

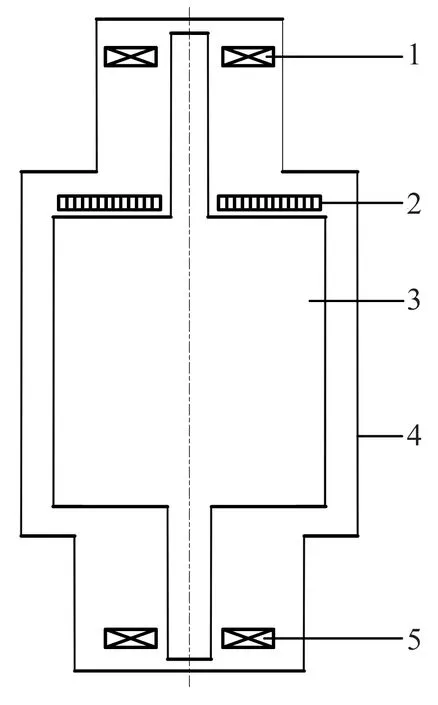
1—上径向主动磁悬浮轴承；2—轴向永磁轴承；3—飞轮转子；4—真空外壳；5—下径向主动磁悬浮轴承。

节点绕x，y轴旋转的角位移；M，G，C，K分别为转子的质量、陀螺、阻尼、刚度矩阵；Fmag为AMB对转子施加的电磁力；n为转子转速；Fd为转子受到的不平衡激振力。

控制系统采用分散PD控制，可得AMB线性化电磁力为[2]

fmag=kii+kss,

(2)

式中：ki，ks分别为AMB的力-电流刚度系数和力-位移刚度系数；i为AMB的控制电流；s为储能飞轮转子在AMB节点处的位移。

2 AMB-储能飞轮转子系统模态及临界转速分析

储能飞轮转子转速为2 000～20 000 r/min，对图1的AMB-储能飞轮转子系统进行模态分析，转子系统的相关参数见表1。

表1 AMB-储能飞轮转子系统仿真参数

转子系统临界转速(频率特征值)是关于支承轴承刚度的函数[16]，可预测临界转速与转子运行速度的接近程度，其变化曲线如图2所示，仅包括转子剪切变形和惯性效应的影响，不包括转子陀螺效应。由图2可知，当轴承支承刚度约为2×107N/m时，前3个模态均表现出明显的斜坡特性，说明此刚度比较合理[17]。在轴承支承刚度为2×107N/m和阻尼为1×104N·s/m下，绘制了转子坎贝尔图(图3)，在陀螺效应影响下，前2阶模态分解为2个随转速变化趋势完全不同的模态，其中随转速升高而增大的为正进动，随转速升高而减小的为反进动。与转速同步振动频率(1×)的交点即为转子一阶临界转速7 213 r/min(120.230 Hz)。飞轮转子在3 000 r/min转速下的前2阶模态振型如图4所示，x，y，z分别为飞轮转子在x，y，z方向上量纲一的位移。其中,一阶反进动频率为120.217 Hz，正进动频率为120.223 Hz;二阶反进动频率为328.988 Hz，正进动频率为417.406 Hz。

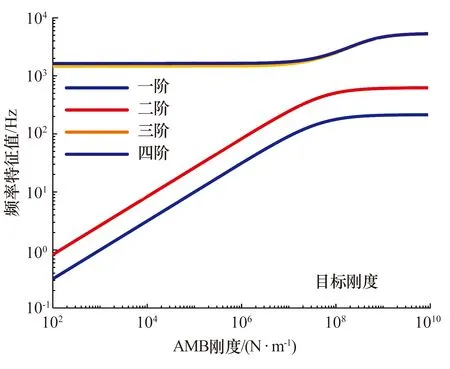
图2 转子频率特征值随AMB刚度的变化Fig.2 Variation of rotor eigenvalues with stiffness of AMB

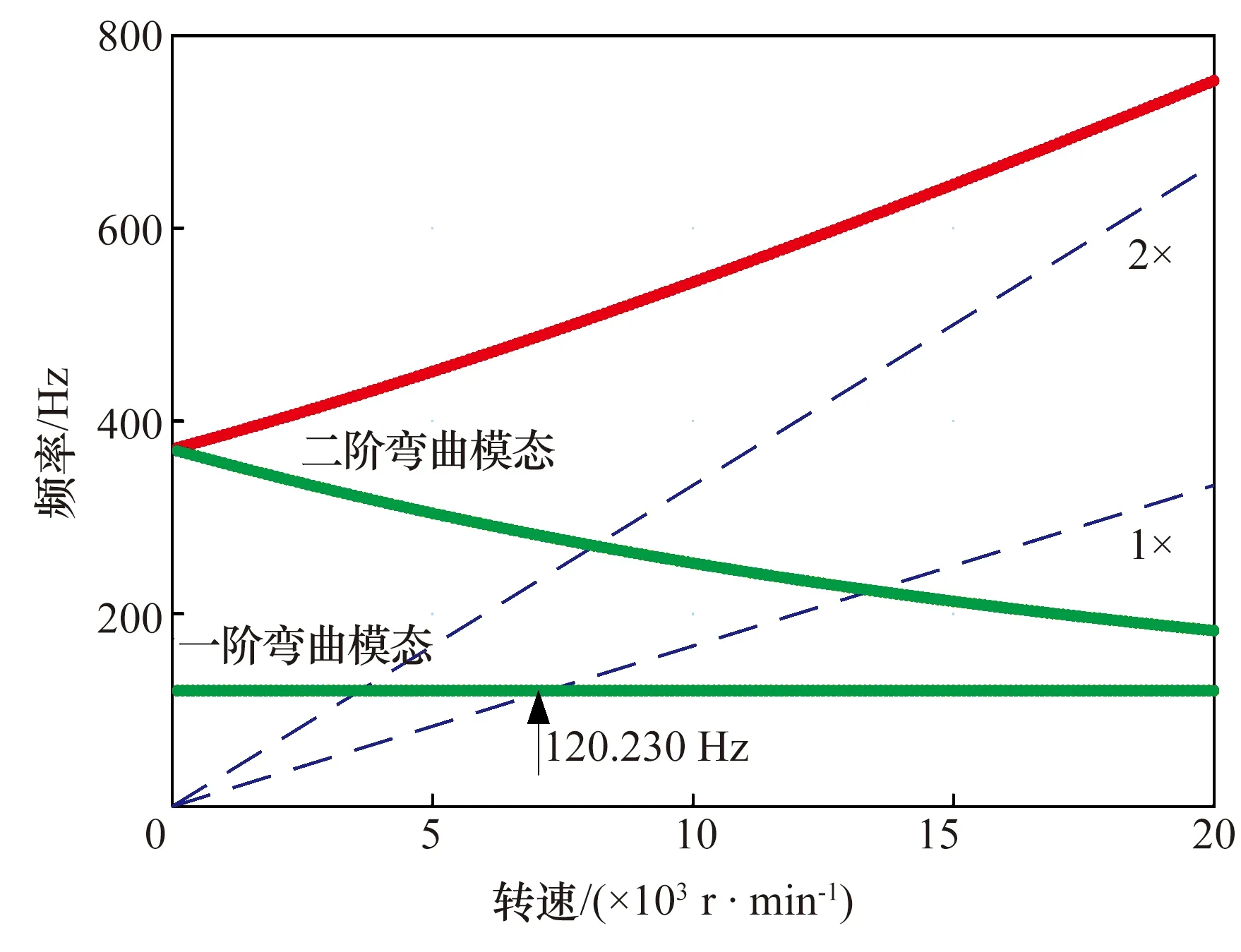
图3 飞轮转子坎贝尔图Fig.3 Campbell diagram of flywheel rotor

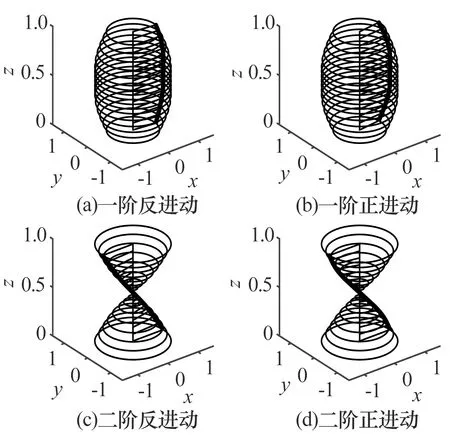
图4 3 000 r/min下飞轮转子的振型图Fig.4 Mode shapes of flywheel rotor under 3 000 r/min

3 基于变步长LMS的不平衡补偿

3.1 基于标准LMS的自适应滤波器

基于标准LMS算法的自适应滤波器原理如图5所示，其迭代公式为

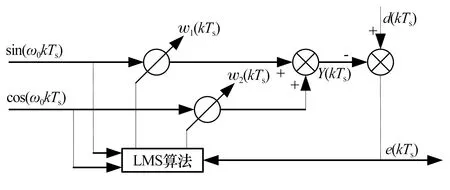
图5 LMS算法自适应滤波器原理Fig.5 Adaptive filter principle of LMS algorithm

(3)

式中：d(k)为输入期望信号；k为采样时刻；a1(k)，a2(k)分别为d(k)中正、余弦成分的幅值；ω为期望信号角频率；Ts为采样周期；y(k)为输出跟随信号；wL1(k)，wL2(k)为迭代权函数；ω0为算法的滤波角频率；e(k)为误差信号；μ为迭代步长因子。LMS算法的目标是当k趋于无限大时，wL1(k)，wL2(k)分别无限趋近于a1(k)，a2(k)，使y(k)无限趋近于d(k)，从而达到消除干扰信号的目的。

本期封面故事聚焦新时代、新青年、新担当，以中国石化团建工作为切入点，希望能引起更多人关心年轻人的成长。

利用Z变换可以得到从d(k)到e(k)的脉冲传递函数为

H(Z)=

(4)

由(4)式知，H(Z)的零点为Z0=e±jω0Ts,其中j为虚数单位，j2=-1。当d(k)为角频率等于ω0的正弦信号时H(Z)=0，表明自适应LMS算法可以完全滤掉输入信号中与ω0同频的正弦信号分量。

3.2 变步长LMS算法

由于AMB-储能飞轮转子处于频繁升降速的工况中，而固定步长的LMS算法在转速频率失配时不能取得良好的滤波效果[18]，需要考虑可实时滤波的变步长LMS算法。

文献[19]针对文献[20]中变步长LMS算法存在的问题提出一种改进算法，其步长因子为

(5)

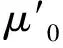
(6)

式中:b为一个正参数，反映了μM受e(k)的影响程度，一般取1～10，b越大说明受影响程度越小。

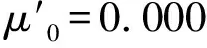
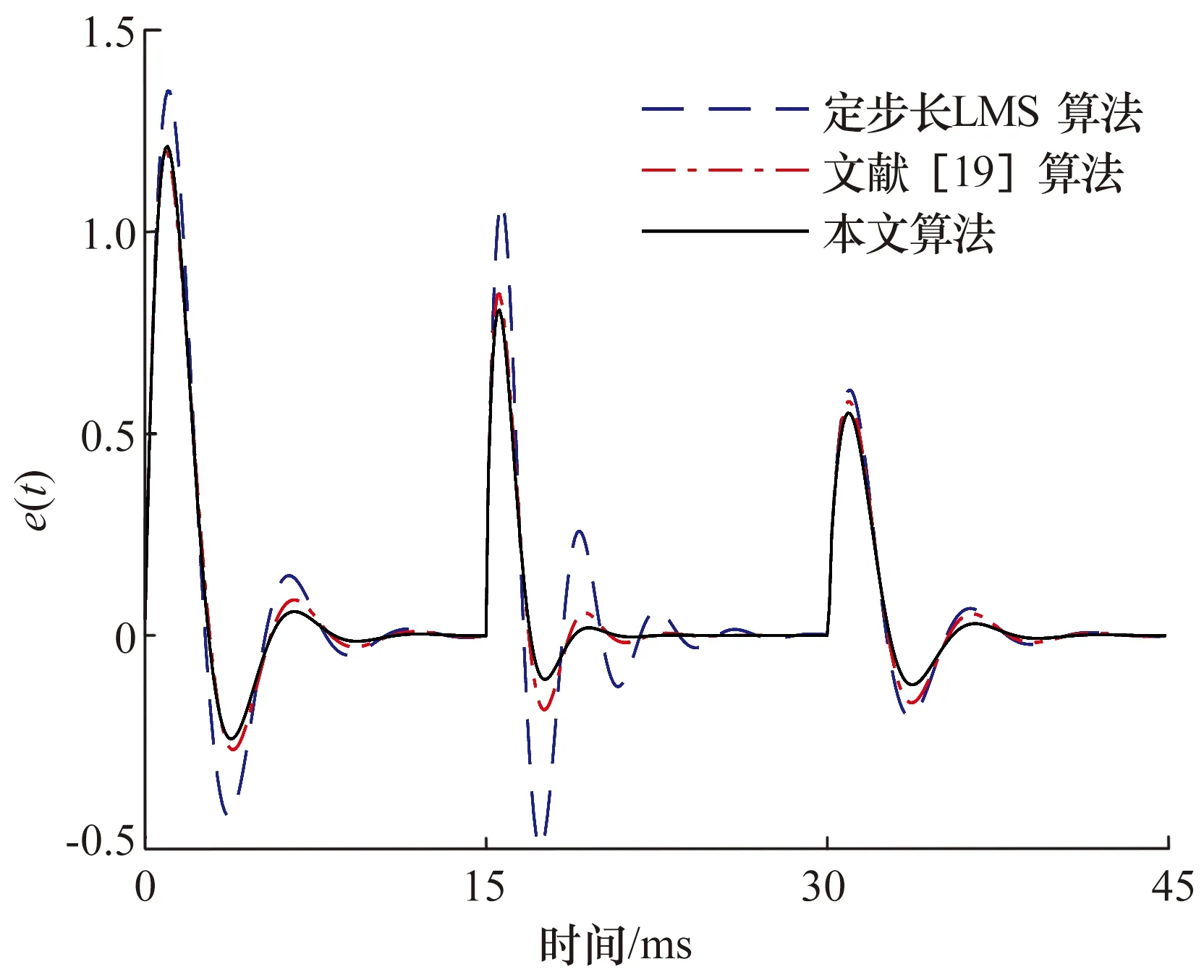
图6 不同LMS算法下的信号误差比较Fig.6 Comparison of signal errors under differentLMS algorithms

3.3 基于自适应变步长LMS算法的不平衡补偿

基于自适应变步长LMS算法的AMB-储能飞轮转子系统不平衡补偿控制的结构框图如图7所示，其中u(t)为转子参考信号，Fd(t)为不平衡产生的激振力，Y(t)为AMB节点处的振动响应。在位移传感器采集的振动信号和参考信号加权后的信号进入分散PD控制器前，通过LMS算法对位移响应信号中与转子转速同频的分量进行补偿，使位移响应信号在进入控制器前就消除了转子同频振动位移干扰。

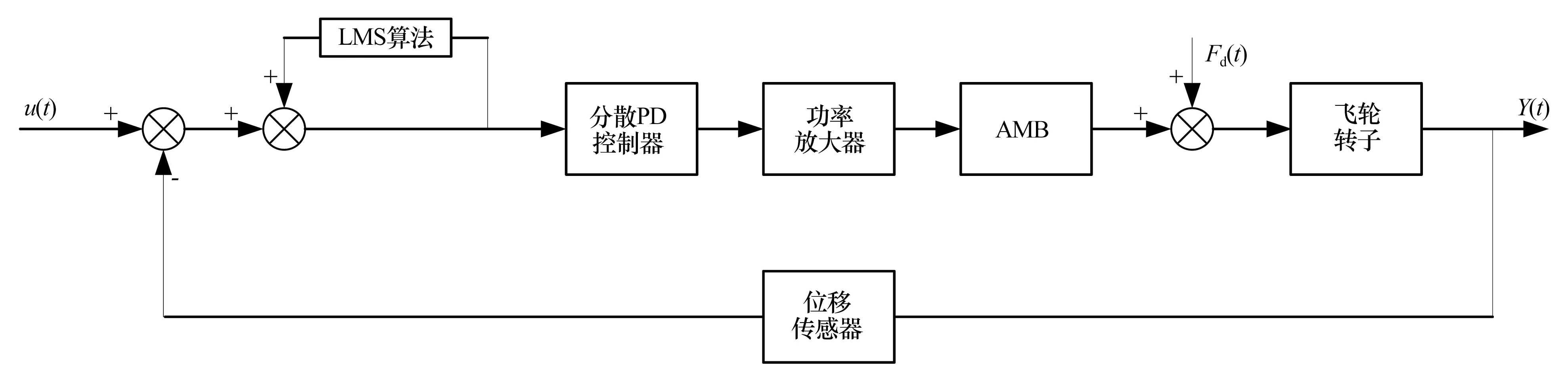
图7 基于自适应变步长LMS算法的AMB-储能飞轮转子系统不平衡补偿控制Fig.7 Unbalance compensation control of AMB-energy storage flywheel rotor system based onadaptive variable step LMS algorithm

4 仿真结果及分析

搭建Simulink模型将上述算法应用于飞轮储能系统，分别在亚临界区(临界转速7 213 r/min以下)和超临界区(临界转速7 213 r/min以上)恒转速工况以及恒加速工况下进行仿真分析。仿真时设定不平衡质量位于转子中心平面，不平衡量取为1×10-3kg·m，初始位置角为0。

4.1 恒转速工况下的不平衡补偿控制

当AMB-储能飞轮转子系统分别在3 000，15 000 r/min的恒转速下运行时，在0.3 s时引入基于自适应变步长LMS算法的不平衡补偿控制。由于仿真模型中转子为中心对称结构，参数完全相同的上、下两端AMB处的转子振动位移响应相同，因此仅给出3 000，15 000 r/min恒转速时上端轴承处的转子振动位移时域仿真结果,如图8所示，其中仿真参数μ0=0.000 000 2，b=10。

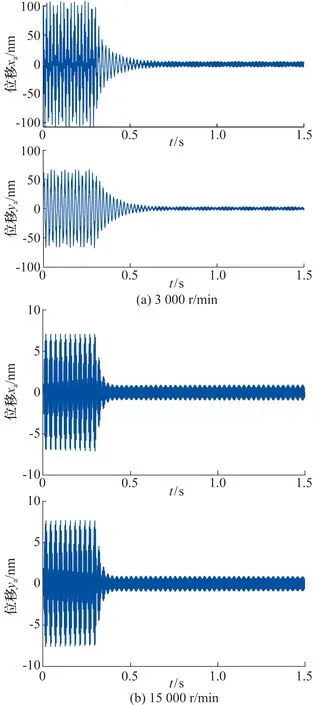
图8 恒转速工况下上端轴承处转子振动位移Fig.8 Vibration displacement of rotor with upper bearingunder constant speed condition

由图8可知，AMB-储能飞轮转子在0.3 s引入基于自适应变步长LMS算法的不平衡补偿控制后，轴承处转子的振动位移大幅降低，在3 000 r/min 恒转速工况时最大振幅由原来的超过100 nm减小到不足6 nm，振幅减小了约94%；而在15 000 r/min恒转速工况时最大振幅由原来的7 nm减小到不足1 nm，振幅减小了约86%。

4.2 恒加速工况下的不平衡补偿控制

为进一步验证本文提出的自适应变步长LMS算法在实际转子运行工况中的控制效果，将储能飞轮转子在加速度a=40π rad/s2的恒加速工况下从0升速至20 000 r/min，仿真结果如图9所示。

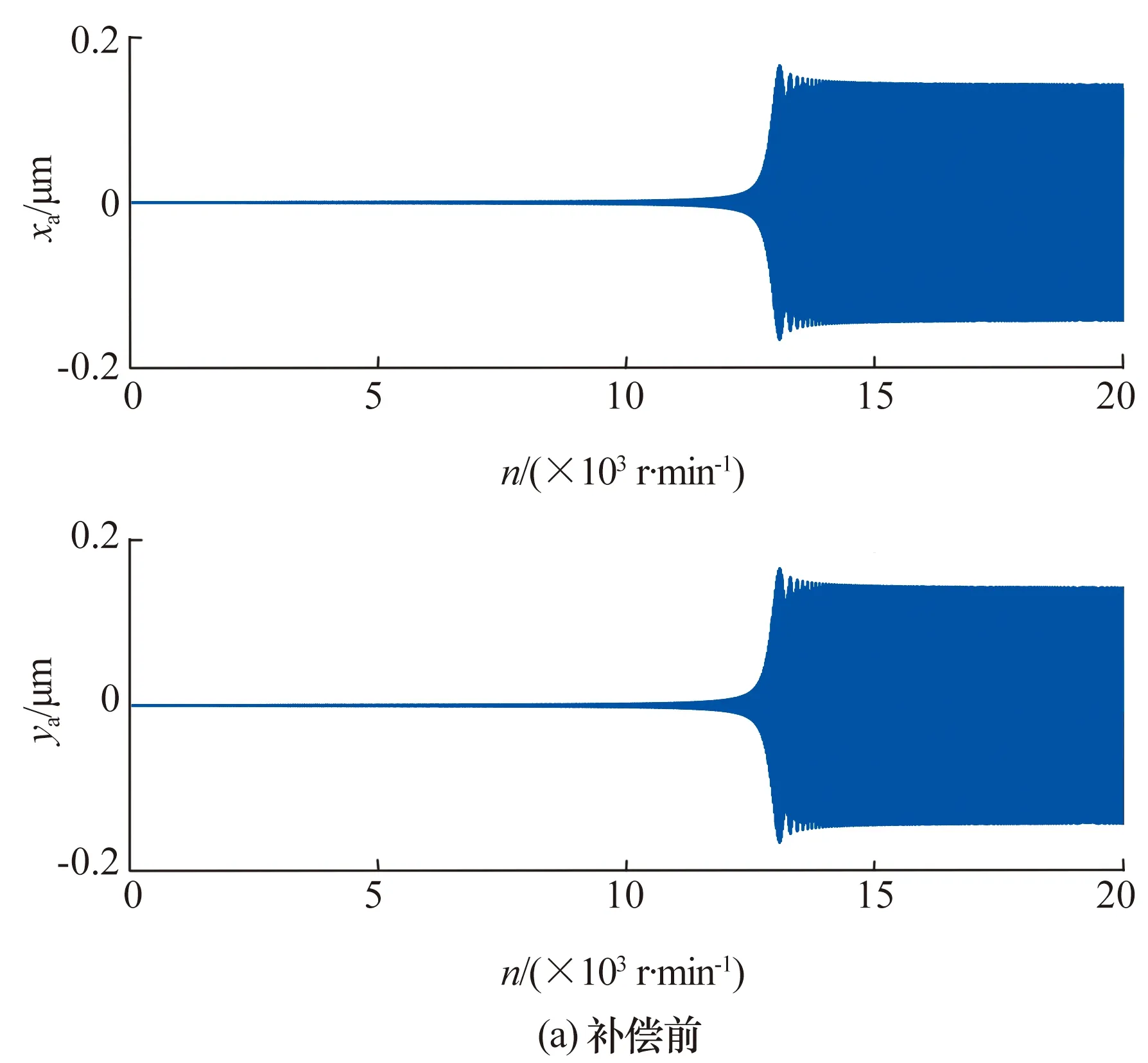
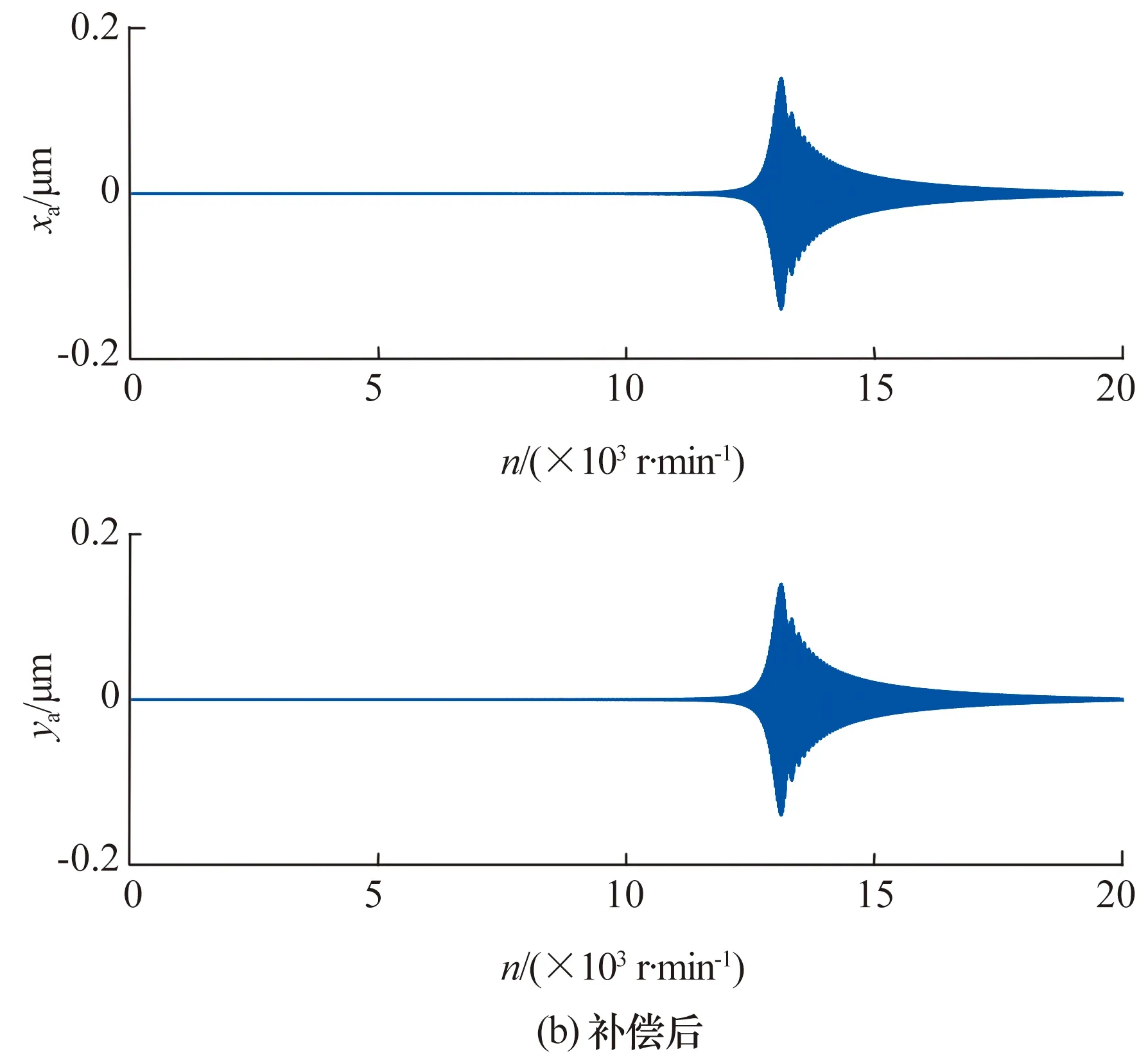
图9 恒加速工况下加入补偿前后上端轴承处转子振动位移Fig.9 Vibration displacement of rotor with upper bearingbefore and after adding compensation underconstant acceleration condition

由图9可知，在整个工作转速范围内，基于自适应变步长LMS算法的不平衡振动控制开启后，转子不平衡振动均有所减小。但在不平衡振动控制开启前，转子越过临界转速之后振动减小甚微，而在不平衡振动控制开启后，转子越过临界转速之后振动大幅减小，控制效果明显。

5 结束语

针对AMB-储能飞轮转子系统中的不平衡振动问题，引入一种基于自适应变步长LMS算法，在反馈信号进入PD控制器前实时补偿同频分量，从而实现不平衡振动补偿控制，保证磁悬浮飞轮转子在整个转速范围内的稳定运行。结果表明，所提出的基于自适应变步长LMS算法的不平衡补偿控制方法能够有效地抑制磁悬浮储能飞轮转子的不平衡振动。