利用弱测量和量子测量翻转方法克服纠缠退相干

丁 东，王 粲，余明星

(华北科技学院，北京 东燕郊 065201)

0 引言

作为量子计算和量子信息中的一种物理资源，量子纠缠态在量子计算[1]、量子密码学[2]、量子隐形传态[3,4]等领域都有广泛的应用。量子态在传输过程中不可避免地会受到环境噪声的影响而产生退相干。退相干通常是指量子系统与环境发生相互作用，导致量子相干性的退化，在某些情况下甚至可能导致量子纠缠的消失[5,6]。因此，减轻或避免环境噪声引起的退相干是量子信息应用中面临的一个重要难题。

目前已有的减轻纠缠态退相干的方法及原理包括纠缠蒸馏协议[7-10]，无退相干子空间[11,12]，量子Zeno效应[13,14]和弱测量和量子测量翻转方法[15-17]等。纠缠蒸馏协议可以从退化的纠缠态中，提取出所需的最大纠缠态。无退相干子空间是指可以从Hilbert空间中找到幺正的子空间，在这个子空间中的状态不会受到特定环境的退相干。量子Zeno效应是指可以通过对量子系统不断地测量来保持量子系统的初始状态以阻止系统的演化，从而减轻退相干。弱测量和量子测量翻转方法是利用弱测量可翻转性质来克服退相干。

常见的退相干信道包括振幅阻尼信道、相位阻尼信道和去极化信道，其中，振幅阻尼退相干适用于许多真实的量子系统，包括具有光子损耗的真空单光子量子比特和具有自发衰变的原子量子比特等。本文主要以振幅阻尼信道为例，研究弱测量和量子测量方法在退相干信道中对纠缠态的保护作用。以Wigner的朋友实验中使用的三粒子纠缠态作为研究对象，计算该量子态在不同退相干强度和弱测量强度下的纠缠度和保真度，探索弱测量和量子测量翻转方法对减轻或避免振幅阻尼量子信道退相干的可行性。

1 理论原理

振幅阻尼信道是一种常见的量子信道，量子态经过振幅阻尼量子信道时会发生能量耗散，造成纠缠特性的损失。以单量子比特为例，假设量子系统的初始态S处于{|0〉，|1〉}基中的任意一个基态，环境E为|0〉E态，振幅阻尼退相干信道对系统的影响为：

|0〉s|0〉E→|0〉s|0〉E，

(1)

(2)

对应到三粒子纠缠态中，振幅阻尼退相干信道对纠缠态的作用即为Mi⊗Mj⊗Mk，i,j,k=0,1。

弱测量和量子测量翻转方法是基于弱测量可翻转的事实，在纠缠态经过量子信道传输之前先对量子系统的纠缠态进行弱测量，将部分|1〉态演化为|0〉态，以降低环境对纠缠态的影响，此过程用非幺正算子表示为

(3)

其中P表示弱测量强度，0≤P≤1且P为实数。对应到三粒子纠缠态中，弱测量算子可表示为

(4)

经过弱测量后的纠缠态，进入振幅阻尼退相干信道进行传输。到达接收方后，应用量子测量翻转对弱测量之后的量子态进行恢复，将部分|0〉态演化为|1〉态。此过程用非幺正算子表示为

(5)

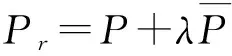
(6)

2 弱测量和量子测量翻转的实现

以三方Wigner朋友实验[21]中的纠缠态

|φ〉abc=[cosθ(|001〉+|010〉-|100〉)

(7)

作为量子系统的初始态。假设三粒子纠缠态经过振幅阻尼信道分别分别发送至Alice、Bob和Charlie的实验室，此时考虑由于纠缠态与环境相互作用产生的退相干。接下来，我们采用弱测量和量子测量翻转方法[22]来避免或减轻纠缠度在振幅阻尼信道中的衰减。

首先考虑不使用弱测量和量子测量翻转方法的情况，三粒子纠缠态|φ〉abc经振幅阻尼退相干后，演化为

(8)

其中ρφabc=|φ〉abc〈φ|abc，为表述简单起见，我们假设三个振幅阻尼量子信道具有相同的退相干强度λ，进而得到系统经过振幅阻尼退相干信道后的密度矩阵

(9)

我们采用计算纠缠度来量化振幅阻尼量子信道对量子态的影响。考虑三体纠缠度量[23]

(10)

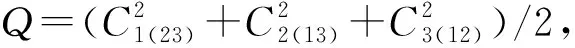
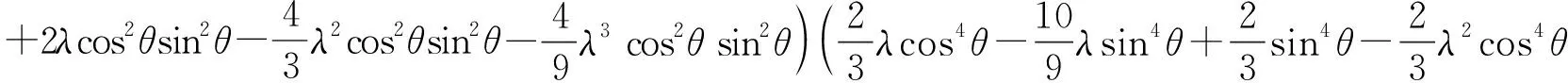
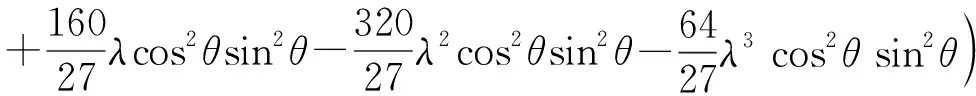
(11)

接下来，考虑使用弱测量和量子测量翻转方法给出针对量子态|φ〉abc克服退相干的效果。在量子态进行传输之前，首先对|φ〉abc进行弱测量，令三个粒子具有相同的弱测量强度P，得到态

(12)

随后，经过振幅阻尼量子信道，同样假设三个量子信道具有相同的退相干强度λ，从而得到密度矩阵

(13)

(14)

得到经过弱测量和量子测量翻转后的量子系统密度矩阵

(15)

(16)

为直观起见，我们绘制可视化图像做进一步分析，如图1所示。图1(a)为弱测量和量子测量翻转前纠缠态的纠缠度随角度θ和退相干强度λ的变化；图1(b)为弱测量和量子测量翻转后纠缠度随角度θ和弱测量强度P的变化(假设振幅阻尼量子信道的退相干强度为λ=0.5)。

由图1可知，未进行弱测量和量子测量翻转前，纠缠度依赖于量子态参数θ和信道强度λ。λ越大，退相干程度越大，当λ达到1时，F123=0，初始纠缠态的纠缠特性消失。经过弱测量和量子翻转测量后，量子系统的纠缠度明显上升，且始终高于未加弱测量和量子测量翻转的量子态，当弱测量强度P达到1时，纠缠态恢复到未进行退相干时的纠缠度F123=0.8889。

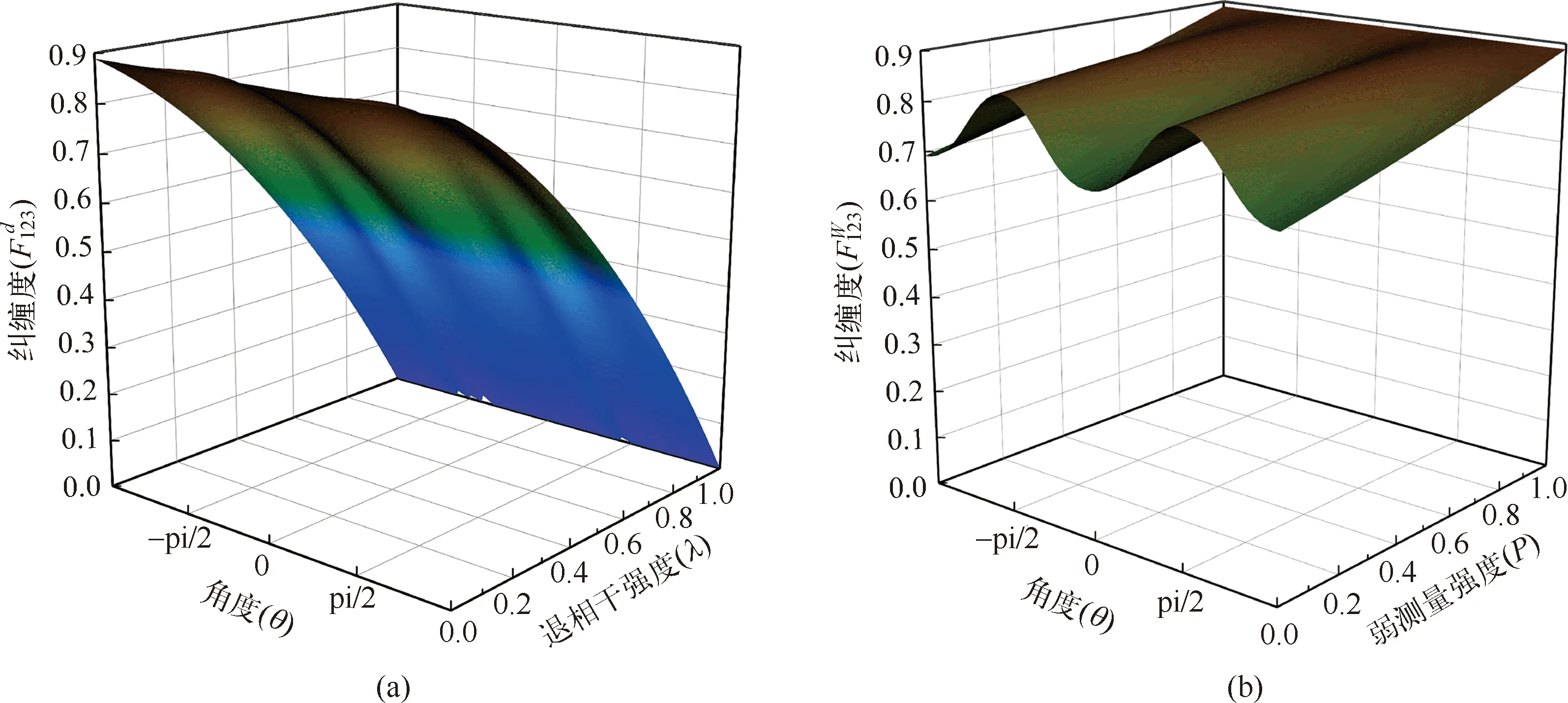
图1 弱测量和量子测量翻转前后纠缠态|φ〉abc的纠缠度变化图

为进一步表明相对于初态|φ〉abc，加入弱测量和量子测量翻转前后纠缠态的还原程度，我们计算保真度

(17)

其中，ρ表示量子系统经过退相干信道演化后的密度矩阵。当系统未进行弱测量和量子测量翻转时，量子系统的保真度为

(18)

当进行弱测量和量子测量翻转后，量子系统的保真度为

(19)

此时，将信道退相干强度设置为λ=0.5，我们得到弱测量和量子测量翻转前后纠缠态的保真度如图2所示。

图2 弱测量和量子测量翻转前后纠缠态|φ〉abc的保真度变化图

由图2可知，保真度随振幅阻尼强度λ的增加而下降。当量子态处于无噪声的理想环境下，即振幅阻尼量子信道的强度λ为0时，不会对纠缠态造成退相干影响，保真度仍为1；当振幅阻尼强度λ达到1时，部分纠缠态保真度降为0，且对于不同参数的量子态，退相干效果不同。经过弱测量和量子测量翻转后，纠缠态的保真度有了显著提高，当θ一定时，弱测量强度越大，保真度越高，甚至当弱测量强度达到1时，保真度可恢复到1。

通过计算量子态的纠缠度和保真度表明，在振幅阻尼量子信道中传输纠缠态|φ〉abc，弱测量和量子测量翻转方法确实能够保护纠缠态，减小退相干影响。

3 结论

(1) 通过弱测量对量子系统的初始状态应用Kraus算子，将系统部分|1〉态坍缩成|0〉态，然后对经过振幅阻尼信道传输后的量子态应用相应的测量翻转将部分|0〉态恢复成|1〉态，从而实现对系统纠缠特性的保护。

(2) 根据弱测量和量子测量翻转前后量子系统的密度矩阵，计算相应纠缠度F123与保真度F。结果表明，弱测量和量子测量翻转方法对保护纠缠态减少退相干的影响具有显著效果，且弱测量强度越大，纠缠态受到退相干的影响会越小。