一种小波提升-DCT变换的电缆数据压缩与传输算法研究

2022-06-08苏瑜蓉

华北科技学院学报 2022年2期

苏瑜蓉，顾涛

(1.华北科技学院安全工程学院,北京东燕郊 065201; 2.华北科技学院计算机学院,北京东燕郊 065201)

0 引言

随着变电站数据监控逐渐远程化，监测点大量监测数据如何进行压缩传输已经变得十分重要。电场数据是电能质量监控方面的重要数据之一，在线路发生故障时，数据范围会发生巨大波动，这一数据特征可以通过有损压缩来实现。目前国内外针对电力领域监控数据比较著名的压缩方式是以色列的基于PQzip技术[1-2]的数据压缩方式，该压缩技术是由Elspec公司提出的一种基于快速傅里叶变换(Fast Fourier Transform，FFT)的有损压缩算法，现主要用于该公司开发的电能质量检测装置中，其压缩比能够达到1000：1。但该技术所使用的FFT变换主要针对如正弦变化的平稳波形压缩，而电场监测数据中包含大量突变值，属于非平稳信号，无法使用PQzip技术进行压缩。因此，需要采用新的压缩方法压缩电场数据。小波变换压缩算法其独特的时频局部特性能够针对电场数据的突变信号，通过阈值处理，将原始信号中的主要信息进行保留，忽略一部分细节，进而实现数据压缩。离散余弦变换(Discrete Cosine Transform，DCT)中，二维DCT变换[3-4]能够有效地将数据集中在矩阵的左上角区域，进而提取重要信息，实现数据压缩。本文通过将一维电场监测数据转换为128×128的二维矩阵，对矩阵进行二维单尺度haar小波提升变换，生成4个64×64的子系数矩阵：低频系数矩阵、高频系数矩阵、垂直方向系数矩阵、对角方向系数矩阵。将得到的系数矩阵进行二维DCT变换，根据压缩比，确定合适的筛选矩阵，将筛选出的非零系数通过一维单尺度haar小波变换进行压缩，进一步调整误差系数，实现电场数据的合理压缩。使用该方法进行数据压缩，解决了单一DCT变换算法中出现的边缘效应，将压缩后数据质量维持在技术指标要求范围内，减轻了电力系统数据传输和存储压力。

1 二维haar小波提升变换

小波提升变换[5-10]也称为二代小波变换，其相较于一代小波变换有计算速度快，操作步骤简单，逆变换易于实现等特点，该算法的基本思想是，将现有小波滤波器分解成多个构造模块，按照步骤完成对信号的频率分解。步骤主要分为三个阶段：分裂、预测、更新，具体实现流程如下：

(1) 分裂。将原始信号分裂成两个互不相交的子集，通常会将信号分裂成偶子集和奇子集两部分，即，

Split(sj)=(ej-1,oj-1)

(1)

其中，原始信号为sj={sj,k},ej-1={ej-1,k=sj,2k},oj-1={oj-1,k=sj,2k+1}.

(2) 预测。通过偶子集和奇子集之间的相关性进行预测，一般是通过偶子集来预测奇子集，并通过奇偶子集之间的差值来反映两者之间的相关程度，这一近似度被称为小波系数，对应于原始信号中的高频部分，相关程度越高，小波系数幅值越小。预测过程如下所示。

dj-1=oj-1-P(ej-1)

(2)

其中，P(ej-1)为预测值，dj-1为真实值与预测值之间的差值。预测算子P也可用预测函数Pk来代替，预测函数可以为偶子集中对应的数据本身，即：

Pk(ej-1,k)=ej-1,k=sj,2k

(3)

也可以是偶子集数据中相邻数据的平均值，

Pk(ej-1)=(ej-1,k+ej-1,k+1)/2=(sj,2k+sj,2k+1)/2

(4)

或是其他复杂函数。

(3) 更新。经过第一步分裂后的子集可能与原始数据集有不同的整体特性，需要通过更新使现有集合与原始数据集保持整体特性的一致，更新过程如下：

sj-1=ej-1+U(dj-1)

(5)

其中，U为更新算子，sj-1为sj的低频部分。与预测函数相同，更新算子也可以取不同的更新函数：

Uk(dj-1)=dj-1,k/2

(6)

或是，

Uk(dj-1)=(dj-1,k-1+dj-1,k)/4+1/2

(7)

通过取不同的预测算子P和更新算子U可得到不同的小波变换。进行haar小波变换时，取预测函数为：

Pk(ej-1)=ej-1,k=sj,2k

(8)

更新函数为：

Uk(dj-1)=dj-1,k/2

(9)

得分解式如下：

Split(sj)=(ej-1,oj-1)

(10)

dj-1,k=oj-1,k-Pk(ej-1)=oj-1,k-ej-1,k=sj,2k1-sj,2k

(11)

sj-1,k=ej-1,k+Uk(dj-1)=sj,2k+dj-1,k/2=(sj,2k+1+sj,2k)/2

(12)

重构式如下：

ej-1,k=sj-1,k-Uk(dj-1)=sj-1,k-dj-1,k/2

(13)

oj-1,k=dj-1,k+Pk(ej-1)=dj-1,k-ej-1,k

(14)

sj=Merge(ej-1,oj-1)

(15)

其中，Merge表示将子集ej-1与oj-1重构为sj。

2 二维DCT变换

DCT变换[11]通常用于信号处理与图像处理中，该变换与离散傅里叶变换相关，是一种限定了输入信号的离散傅里叶变换。在信号处理中，DCT变换能够将原始信号中的重要信息转换为一组主要集中于矩阵左上角的系数矩阵，进而方便下一步操作。其中二维DCT正变换公式如公式(16)所示：

(16)

其中，x,y,u,v=0,1,…,N-1。

二维DCT逆变换公式如公式(17)所示：

(17)

其中，x,y,u,v=0,1,…,N-1。

在第一节中，经过一次二维小波提升变换后得到4个64×64的系数矩阵，需要将4个系数矩阵分别进行二维DCT变换，公式(16)(17)中的N可取64.

3 小波提升-DCT变换压缩与传输算法

3.1 压缩算法

小波提升-DCT变换压缩算法[12]具体步骤如下，步骤流程图如图1所示：

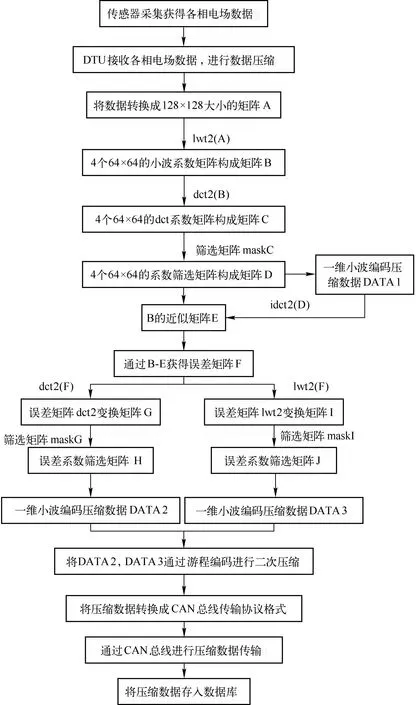
图1 压缩算法步骤流程图

第一步，DTU接收传感器采集到的一维电场数据后，将其转化为128×128大小的矩阵A；

第二步，通过单尺度二维haar小波变换将128×128的原始数据转换为4个64×64的系数矩阵，4个系数矩阵所构成的128×128的矩阵记作矩阵B；

第三步，将4个系数矩阵分别做二维DCT变换，将系数有效集中至矩阵左上角，经DCT变换后构成的128×128矩阵记作矩阵C；

第四步，构建筛选矩阵。由于经过DCT变换后的矩阵，主要信息都集中在左上角。因此，在进行系数筛选时，矩阵行(或列)下标较为靠后的元素在构建筛选矩阵时被置零的优先级要大于矩阵行(或列)下标较为靠前的元素；

第五步，将筛选后的系数矩阵D中非零元素转换为一维数组，进行一维haar小波变换，将数据压缩，得到压缩数据DATA1；

第六步，将压缩数据还原后的系数矩阵E与矩阵B做差值得到误差系数矩阵F；

第七步，将误差系数矩阵F执行三至五步，得到压缩数据DATA2；

第八步，将误差系数矩阵F执行第二步，第四步，第五步，得到压缩数据DATA3；

第九步，通过压缩数据调整误差系数矩阵，重构原始数据，得到矩阵B′。矩阵B′计算方式如下：

B′=E+F

(18)

其中，

E=IDCT2(ILWT(DATA1))

(19)

F=α(IDCT2(ILWT(DATA2)))+β(ILWT2(ILWT(DATA3)))

(20)

其中，α,β分别为DCT系数调节因子，小波系数调节因子，当确定压缩比后，可计算得出压缩后的数据个数S，按照矩阵C筛选4个系数，矩阵F通过小波变换和DCT变换的矩阵分别筛选出(S-4)/2个系数的方式构建筛选矩阵，获得压缩数据；

第十步，通过游程编码将压缩数据进一步压缩，在使用游程编码时，规定当压缩数据小数点后两位数据相同时即为相等数据；

第十一步，以上压缩步骤在DTU中实现，将压缩后的数据经CAN总线传输到后台接收端，最终存入数据库。

3.2 CAN总线协议

通过小波提升-DCT变换压缩算法得到压缩数据后，需要设定CAN总线传输协议，确保压缩数据的正常传输。按照CAN总线通信协议每帧传送8个字节的要求制定具体传输协议见表1。

表1 CAN总线传输协议

第一字节：支路号。如1，2 ……

第二字节：最高两位为相序，01******为A相，10******为B相，11******为C相，低6位为状态位，**000000为正常状态，**000001为接地状态，**000010为短路状态，**000100为电流变化状态，**001000为电场变化状态， **010000为弧光接地，**100000为断线

第三字节：矩阵号。如1，2 ……

第四字节：帧号。根据压缩比，压缩数据共需传输1024字节，因此共需要传送256帧数据，即帧号为1-256.

第四字节至第八字节：电场压缩数据。

3.3 仿真结果

实验通过设定压缩比，确定压缩数据大小，进行参数α,β的调整。当压缩比确定为819.2：1，546.13：1，327.68：1时，对应DCT系数调节因子分别为α=3.10,1.93,1.73，小波系数调节因子分别为β=0.79,1.2,1.0，原始数据与解压缩数据之间数据恢复百分比误差范围分别维持在8.6571～0，8.3657～0，8.5354～0之间，小于百分之五的误差占比分别达到76.21%，82.35%，88.79%。最终确定当压缩比为16.603：1时，原始数据与解压缩数据之间数据恢复百分比误差范围维持在0～6.0374之间，其中，小于百分之五的误差占比可达92.86%，能够达到电场技术指标误差范围不超过±10%的要求。压缩前后数据局部放大对比图如图2所示。