转化思想在初中数学建模教学中的应用

梁燕冰（广东省佛山市南海区狮山镇罗村第二初级中学）

数学建模的过程是“分析问题—合理假设—分析模型—找到方法—建构模型—检验模型—解决问题”。培养学生的数学建模能力是教师的重要任务之一，然而提起数学建模，很多学生不知道其中的内涵，更不用说掌握建模的方法。下面，笔者谈谈如何将数学建模问题归类与转化成学生熟悉的、易懂的数学问题，从而更好地帮助学生理解数学建模并掌握相关方法。

一、转化为方程问题的数学建模

方程是指含有未知数的等式。在对实际问题建模的过程中会经常涉及一些等量关系，此时可以在数学建模中构建方程模型。

例1 现有两块大小相同的长方体木板，用它们来测量桌子的高度，如图1 放置并测量数据，然后改变木板的放置方法；如图2 放置并测量数据，试计算桌子的高度。

图1

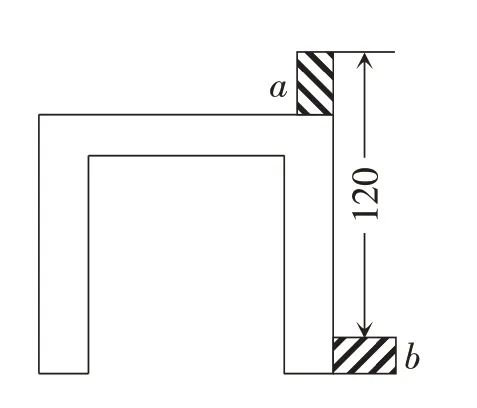
图2

教师引导学生先假设木块的长、宽和桌子的高度，然后让学生小组讨论并汇报。

解：设木块的长为acm，宽为bcm，桌子的高为xcm，

依题意，得b+x-a=100，a+x-b=120。

两式相加，消元求出x=110。因此，桌子的高度为110 cm。

【反思】经过师生共同探讨，学生感受到了什么是数学建模，也体会到了求解成功的喜悦。同时，通过例题教师还总结了在生活中测量桌子高度的方法，让学生感受到了学以致用的乐趣。

二、转化为几何问题的数学建模

几何与人类的生活密切相关。实际生活中的数学建模问题，尤其涉及角度问题时，需要转化为常见的几何问题，利用锐角三角函数、勾股定理等知识进行求解。

例2如图3，有一把搭在墙上的梯子长4 m，其与地面所成的角度为45°。当把它调整为与地面成60°角时，求梯子的顶端沿墙面上升了多少。

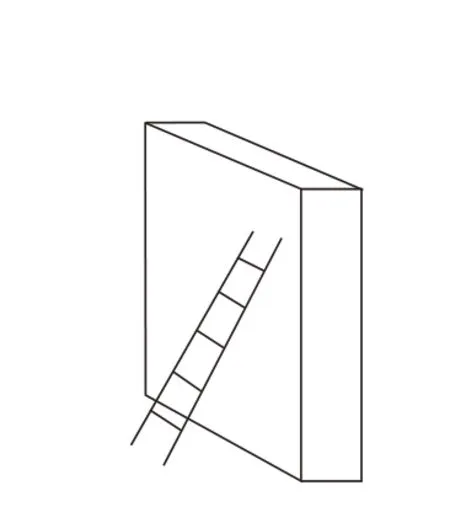
图3

教师指导学生把梯子的两种摆放情况简明地画出来（如图4），然后师生一起分析并完成解题过程。

图4

解：梯子的顶端沿墙面上升的高度为BC=

【反思】教师引导学生依据题设画出几何图形，把题目中看似不容易表示的“梯子的顶端沿墙面上升了多少”等价转化为“求线段BC的长度”，化繁为简。此题是学生在学习三角函数时的常见题型，计算过程不复杂，重在让学生学会把生活中的一些数学建模问题用几何图示分析并求解，让学生不再认为数学学习枯燥。

三、转化为不等式相关的数学建模

对于生产决策、购买方案、统筹安排等现实生活中的问题，可以通过分析数据，然后转化为不等式进行计算解决。

例3班主任让小明和小红用70 元奖励金去购买钢笔和笔记本共20件，奖励平时表现突出的学生。已知钢笔每支5元，笔记本每本1元，班主任要求钢笔的数量不少于笔记本的数量，共有多少种购买方案？

教师先引导学生理解题意，并提醒学生注意取值范围的限制，然后师生共同完成解答过程。

解：设购买笔记本x本，依题意，得

教师引导学生根据实际情况取整并检验，得出共有3 种购买方案：钢笔12 支，笔记本8 本；或者钢笔11支，笔记本9本；或者钢笔10支，笔记本10本。

【反思】涉及方案的建模题目对于很多学生来说都比较困难。此例题中，教师引导学生把题目中的两个条件“购买金额不超过70元”和“钢笔的数量不少于笔记本的数量”直接转化为不等式，列出不等式组来求解，而取整数其实就是对模型的检验。此题让学生经历了数学建模的整个过程，不仅让学生体会了数学建模的含义，还让学生对数学的学习更有兴趣和信心。

四、转化为函数问题的数学建模

在现实生活中，最大获利、成本最低等问题可以尝试构建函数模型来求解。

例4某养猪场若每天投入3.2 元，则可让一头60 kg重的生猪每天增加2 kg。已知当时生猪的市场价格为每千克20元，但同时估计每天每千克生猪价格下降0.4 元。对于该养猪场而言，当时60 kg 重的生猪在什么时候出售可以获得最大利润。

解：设在t天后出售生猪，养猪场能获得最大利润，此时养猪场的投入为3.2t元，每头生猪能卖( 20-0.4t)( 6 0+2t)元，最大利润为( 2 0-0.4t)( 6 0+2t)-3.2t=1 200+40t-24t-0.8t2-3.2t= -0.8t2+12.8t+1 200=-0.8(t2-16t)+1 200= -0.8(t-8)2+1 251.2。所以，在8 天后卖出生猪，可以获得最大利润。

【反思】此题是一道关于二次函数的最值问题，教学时应该引导学生配方，根据实际情况来检验答案的合理性。此题中，经过8 天后，虽然后来投入是8 ×3.2=25.6（元），但产出比原本的60×20=1 200（元）多了51.2元，因此是可行的。

五、转化为统计问题的数学建模

统计知识在经济、管理等多领域被广泛应用，实际生活中出现的个数和成绩等问题，常常需要转化为统计问题，再利用有关知识加以解决。

例5 在日常生活中，我们经常会遇到用空瓶换汽水的问题。如果用m个空瓶可以换1 瓶新的汽水，当原有n瓶汽水时，最多能喝到多少瓶汽水呢？

教师引导学生列举一些简单、具体的实际情况来分析，如现有10 瓶汽水，用3 个空瓶可以换1 瓶新的，最多能喝到多少瓶汽水呢？师生共同探究得出答案：可以借来1个空汽水瓶，连同最后剩下的2个空汽水瓶一起再换1瓶新的，喝完后再还回去1个瓶子，所以最多能喝14+1=15（瓶）。教师引导学生从特殊到一般，共同解答此题。

解：每m个空瓶换1 瓶饮料，则当拥有(m-1) 个空瓶时，就可以借1个瓶子从而换得新的1瓶，然后把借来的瓶子归还。因此，当喝完n瓶饮料得到n个空瓶后，又能得到瓶饮料，总共最多能喝（瓶），除不尽时则向下取整数。

【反思】题目中的量是抽象的m和n，没有具体数量，看似很复杂，教师用特殊化方法，一步步地引导学生分析题意，找到解题方向，并解决特殊情况，然后从特殊情况出发探讨一般情况，把看似困难的数学建模问题转化为容易解决的统计问题。

在教学实践中，教师要善于引导学生把生活中的问题转化为方程、几何、不等式、函数、统计类问题，并让其经历数学建模的过程，从而让学生更好地学习数学建模，不断提高数学建模能力。