膨胀土地区自平衡试验负摩阻力转换系数研究

2022-06-07欧孝夺吕政凡陆小金秦金喜

公路工程 2022年2期

欧孝夺,吕政凡,陆小金,江杰,李胜,秦金喜

(1. 广西大学土木建筑工程学院，广西南宁 530004；2. 工程防灾与结构安全教育部重点实验室，广西南宁 530004；3. 广西金属尾矿安全防控工程技术研究中心，广西南宁 530004；4. 同济大学土木工程学院，上海 200092)

1 概述

随着工程建设的发展，桩基础因其拥有独特的优势而得到了广泛应用，然而各种复杂条件下应用的桩基础对基桩承载力试验提出了挑战。自平衡试桩法由于其独特的加载方式，而具备试验简单易行、操作安全、不受场地和吨位制约的优点，极大地节省了检测成本和检测时间，是一种先进的检测技术[1]。采用自平衡法确定试桩极限承载力时，需将上、下2段桩按2根独立的受检桩取极限值，再采用等效转换方法获得自平衡试桩的极限承载力。其中负摩阻力转换系数的取值是自平衡试桩承载能力准确与否的关键所在。

目前规范规定当无可靠比对试验资料和地区经验时，不同土质条件下的转换系数可取0.8～1.0，其取值是针对各个地区给出的建议值，这种考虑下各地区土质差异的取值方法偏保守。李小娟[2-3]等以某桥梁的3根钻孔灌注桩为试验对象，先后进行自平衡静载试验和传统静载试验，通过对比2种测试方法的极限侧摩阻力值，得出砂性土、黏性土中的转换系数分别为0.6～0.7、0.7～0.8的结论。LEE[4]等通过室内模型试验对比抗压桩与抗拔桩侧摩阻力的差异，得到砂土中抗拔桩桩侧摩阻力为抗压桩的0.56倍。KIM[5]等研究了由侧摩阻力引起的自平衡法与传统静载法桩身压缩量之比，研究表明桩的长径比、土质和排水状况对桩侧摩阻力的发挥存在影响。张新蕾[6]、陈长流[7]、赵天时[8]通过现场试验得到了自重湿陷黄土桩基负摩阻力的分布规律。周奎[9]、刘辰麟[10]、李心平[11]则通过现场试验结合数值模拟的方法分析了黄土湿陷性差异、厚度、抗剪强度和桩体参数等因素对黄土地区负摩阻力的影响。齐静静[12-14]等通过现场试验研究了湿陷黄土地区的自平衡试桩负摩阻力的发展规律。HOONIL[15]等采用数值模拟的方法，得出不同长径比和土体弹性模量对应的转换系数。从上述文献可以看出，特殊土负摩阻力的对比试验主要集中在对湿陷性黄土的研究，而对膨胀土的研究尚不多见。针对实际工程中特殊土的负摩阻力取值，设计者大多参照规范中相似土层取值，例如膨胀土按黏土取值。显然这是不准确的，这将极大影响自平衡静载试验技术在膨胀土地区的准确性。

膨胀土是一种遇水膨胀失水收缩的特殊性土。在膨胀土地区中进行自平衡静载试验确定极限承载力时，需要通过等效转换方法确定，但自平衡规范[16]并未针对膨胀土特性给出相应负摩阻力转换系数。因此，研究膨胀土中自平衡试验负摩阻力转换系数，不仅对膨胀土地区自平衡静载试验的准确性有积极作用，也有利于自平衡静载试验技术在特殊土分布地区推广应用，具有显著的现实意义。本文研究成果可为膨胀土地区自平衡试验负摩阻力转换系数γ取值提供参考。

2 模型试验

2.1 试验装置

试验装置包括模型箱、模型桩、底座、支架、砝码、浸水装置和数据采集系统(包括压力传感器、百分表和应变仪)，具体布置如图1、图2所示。试验所用模型箱为高度880 mm、直径580 mm、壁厚3 mm的钢桶，桶底加焊3 mm的圆形钢板以防止夯土造成桶底变形；为方便注水管的连接，在钢桶作业侧壁距底部20 mm处预留孔径为20 mm、向外延伸40 mm的连接口；模型箱底部的孔与PVC管间设有O型线圈，在浸水试验时作防水措施，在加载时取下O型线圈使试桩自由滑动[17]。

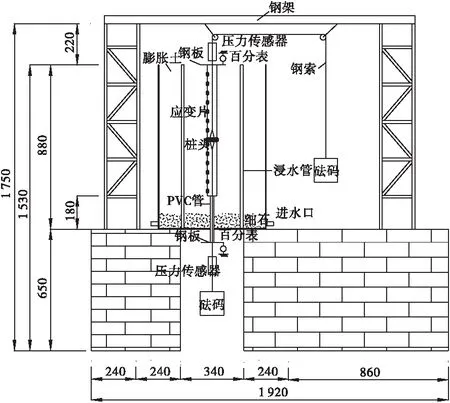
图1 试验装置正面图(单位：mm)Figure 1 Front view of test equipment(Unit:mm)

图2 试验装置侧面图(单位：mm)Figure 2 Side view of test equipment(Unit:mm)

试验采用的传统静载模型桩和自平衡试验模型桩的上、下2段桩均为铝合金制空心管，外径25 mm、壁厚2 mm。试验桩入土深度为670 mm，未入土部分长30 mm，另在桩顶以下20 mm处一侧预留10 mm圆孔，用于引出应变片连接线，如图3所示[17]。

图3 模型桩实物图Figure 3 Model pile drawing

2.2 试验用土

试验用膨胀土取自广西南宁地区某工地，取样深度范围为2～2.5 m，通过室内试验测得土样天然含水率为18%，干密度为1.48 g /cm3，属于弱潜势膨胀土，其物理参数如下：自由膨胀率48.5%，天然含水率20.02%，液限64.0%，塑限32.0%，塑性指数32.0%，天然密度1.48 g/cm3。采集的扰动土通过烘干、粉碎制成初始含水量为18%的土样用于填筑，控制实际与设计含水率、干密度偏差不超过±1%。模型试验土体按每层100mm进行分层填筑，并对每层填土取样测其含水率，称取土样后采用人工夯实至干密度为1.48g /cm3。

2.3 试验内容

试验分为2组，第1组为膨胀土未浸水情况下，对传统静压桩和自平衡试桩进行逐级加载，直至试桩破坏；第2组为膨胀土浸水膨胀至土体饱和后，再对传统静压桩和自平衡试桩进行逐级加载，直至试桩破坏。

3 试验结果与分析

通过Q-S曲线确定自平衡试桩极限承载力主要有以下2种情况：①对于有明显突变的Q-S曲线，取突变点前一级荷载作为极限承载力；②对于无明显突变的“缓变”型Q-S曲线，极限承载力可取累计位移达到40 mm时所施加的某一级荷载。

提取试验所得未浸水工况下和浸水工况下传统静压桩、自平衡试桩荷载-沉降曲线(Q-S曲线)如图4、图5所示，向上位移为正，向下位移为负，试验Q-S曲线均存在明显的突变点。由此分析：

a.未浸水工况下：对于传统静压桩，桩顶累积位移为13.2 mm，加载前期位移随荷载增加呈缓慢增加趋势，当荷载增加至1 360 N时，位移增量有增大趋势，荷载继续增大至1 750 N时，位移已达15.0 mm，卸载后回弹量仅为1.8 mm，已超出弹性工作范围，可判定试桩已发生破坏，取1 570 N为静载试桩极限承载力。对于自平衡试桩，上段桩与下段桩的Q-S曲线发展趋势基本相同，分别取上下段曲线的拐点处对应荷载为极限荷载，上下段桩极限承载力分别为660 N和758 N。

b.浸水工况下：对于传统静压桩，桩顶累积位移为5.4 mm，加载前期位移随荷载增加的趋势缓慢，当荷载增加到1 200 N时，位移增量有增大趋势，继续增大1 320 N时位移已达10.0 mm，卸载后回弹量仅为2.1 mm，已超出弹性工作范围，可判定试桩已发生破坏，取1 200 N为静载试桩极限承载力。对于自平衡试桩，上段桩与下段桩的Q-S曲线发展趋势基本相同，分别取上下段曲线的拐点处对应荷载为极限荷载，上下段桩极限承载力分别为378 N和578 N。

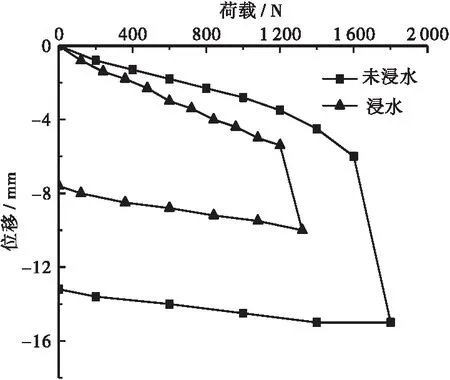
图4 2种工况下传统静压桩Q-S曲线Figure 4 The Q-S curves of traditional static pressure pile under two working conditions

图5 2种工况下自平衡试桩Q-S曲线Figure 5 The Q-S curves of self-balancing test pile under two working conditions

同时根据规范[16]中的单桩竖向受压承载力确定方法，单桩的竖向极限承载力应取Q-S曲线出现突变点时对应的荷载值或s-lgt曲线尾部出现明显下弯曲时的前一级荷载值。提取沉降-时间对数曲线如图6、图7所示。综合分析图4～图7，可以推断未浸水工况下传统静压桩，及自平衡上、下段桩竖向极限承载力为1 570、660、758 N；在浸水工况下传统静压桩，及自平衡上、下段桩竖向极限承载力为1200、378、578 N。

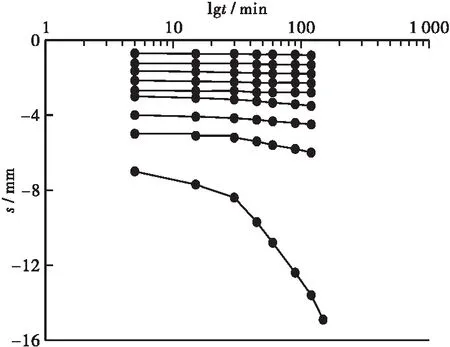
(a) 未浸水工况

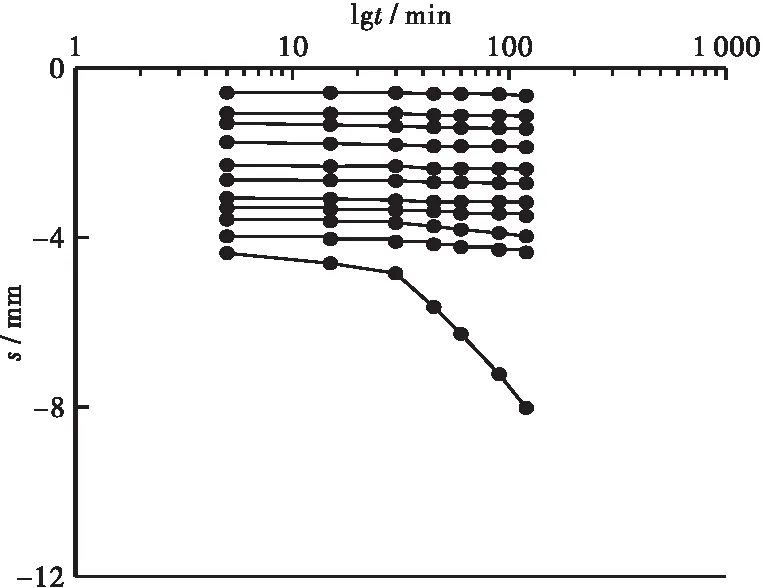
(b) 浸水工况

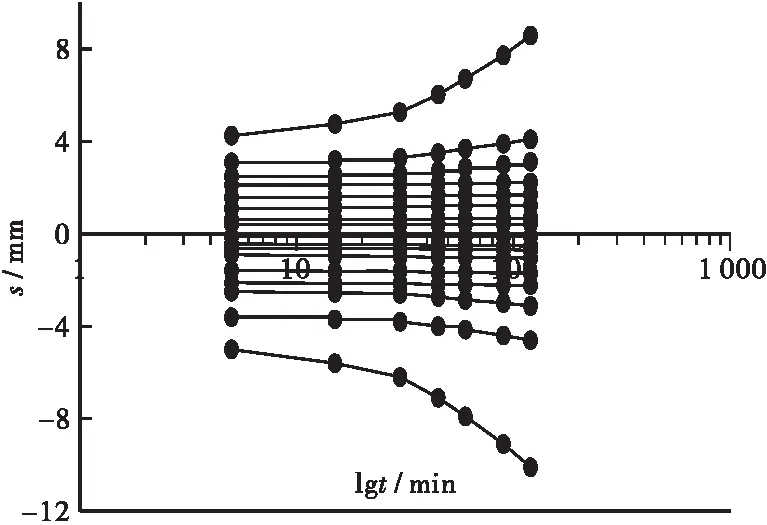
(a) 未浸水工况

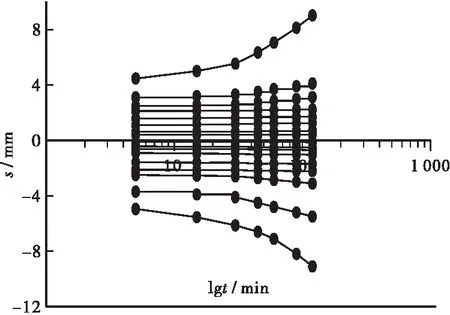
(b) 浸水工况

4 负摩阻力转换系数确定

4.1 转换系数的确定

本文模型试验采用的自平衡试桩与传统静压桩桩长、桩径均相同，且是在同样边界条件下完成加载的，可以认为试桩极限承载力相同，故将传统静压桩极限承载力视为自平衡试桩整根桩极限承载力。采用式(1)计算试桩负摩阻力转换系数，求得未浸水时负摩阻力转换系数为0.82，浸水时为0.63。

(1)

式中:Q为传统静压桩加载极限值；Q上、Q下分别为自平衡试桩上、下段加载极限值；W为上段桩自重；γ为受检桩的负摩阻力转换系数。

4.2 自平衡试验等效转换结果

为验证对比试验所得转换系数γ的可靠性，将自平衡试桩结果向传统静载试验结果进行等效转换。试验结果转换分为2个部分，第1部分为荷载转换，可通过式(1)实现。第2部分为位移转换，静压试桩位移包括桩端土压缩变形与桩身压缩变形，其中桩身压缩变形量为桩端阻力与桩侧摩阻力引起的压缩变形量之和，按式(2)、式(3)、式(4)计算。因等效静载桩下段与自平衡桩下段受力情况相同，且位移相等，直接取下段桩位移s下为桩端土压缩变形。等效后整桩位移s见式(5)。

(2)

(3)

(4)

s=s下+Δs

(5)

式中：Δs为上段桩桩身压缩变形量；Δs1为在桩端阻力作用下上段桩桩身的压缩变形量；Δs2为在桩侧摩阻力作用下上段桩桩身的压缩变形量；Ep为桩身弹性模量；Ap为桩身截面面积；L为上段桩长度。

在上式中，特别注意的是式(4)中Q下荷载的取值应采用位移s上=s下所对应的荷载值。为了直观显示不同转换系数对转换结果的影响，假设浸水前后转换系数不变，γ取0.7。等效转换结果如图8、图9所示。

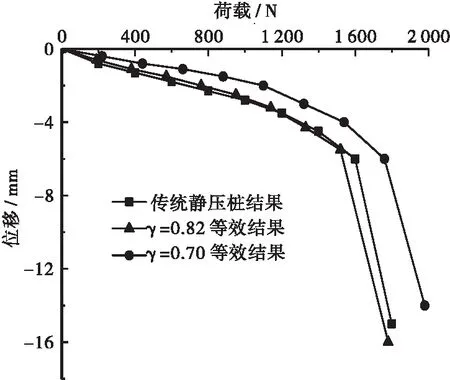
图8 未浸水工况下自平衡等效曲线与传统静压曲线Figure 8 The curves of equivalent test pile and traditional static pressure pile without flooding

图9 浸水工况下自平衡等效曲线与传统静压曲线Figure 9 The curves of equivalent test pile and traditional static pressure pile in flooding condition

由图8、图9可见，浸水前γ取0.82，浸水后γ取0.63，自平衡等效转换Q-S曲线与传统静压试桩Q-S曲线匹配程度较好。当假设浸水前后转换系数不变，γ取0.7，转换曲线与传统静压曲线有一定的偏差，说明γ取值对转换结果影响较大。

5 数值模拟对比与不同含水率分析

本文在国内学者普遍认可的温度场等效湿度场理论基础上，采用有限差分软件FLAC3D对膨胀土负摩阻力转换系数取值的参数影响进行分析。在土中设置热源使土体加热膨胀，设定其发热功率即热膨胀率来模拟膨胀土的膨胀系数。求解过程设定温度计算为主步，静力计算为从步，实现热力耦合来对膨胀土桩基静载试验的模拟。

5.1 模型建立

5.1.1温度场等效湿度场理论

FLAC3D中的温度模块可以模拟材料中的瞬态传导，以及因温度发展而产生的位移与应力，即温度应力导引起应变。FLAC3D中的能量方程表达式为：

(6)

式中：qi,i为qi在i方向的导数，即热流量向量梯度,W/m3；qv为体热源强度,W/m3；ζ为单位体积所含热能,J/m3；t为时间。

温度会随着能量储存和体积应变的改变而发生变化，其本构关系可表示为：

(7)

式中：Mth和βth表示材料常量；T为温度,℃。当βth=0，且Mth=1/ρCV，ρ为密度,kg/m3，Cv为恒定体积下的比热,J/kg·℃;代入式(7)得到：

(8)

将式(8)代入式(7)，可得能量平衡方程：

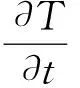
(9)

对于静态、均匀的各向同性实体，傅里叶定律表达式为：

qi=-λTi

(10)

式中:λ为热导率,W/(m·℃)；Ti为T在i方向的导数，即温度梯度,℃/m；当qv=0，将式(9)代入式(10)可得热传导微分方程：

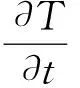
(11)

FLAC3D的热力耦合是基于温度改变引起单元的应变而实现的，温度引起的应变增量Δεij与温度该变量ΔT的关系为：

Δεij=αΔTδij

(12)

式中：α为温度线膨胀系数；ΔT为温度增量,℃；δij为Kroneeker delta函数。

在湿度应力场理论中，岩土吸水膨胀的方程可表示为：

(13)

式中：Δεw为吸水膨胀引起的应变增量；β为膨胀土的膨胀系数；Δw为含水量变化量；δij为Kroneeker delta函数。联立式(12)、式(13)可得：

(14)

基于上述理论，通过前期进行的室内膨胀土自由膨胀率试验所得的膨胀土的膨胀系数β，利用式(14)，及可求得数值模拟计算所需的温度线膨胀系数α。在土中设置热源使土体加热膨胀，设定其发热功率即热膨胀率来模拟膨胀土的膨胀系数，进而利用FLAC3D温度模块对膨胀土桩基的受力过程进行热力耦合分析。

5.1.2相关参数及边界条件

对第1节模型试验进行数值模拟分析，建立尺寸为0.25 m×0.25 m×0.85 m且中心开直径0.025 m深度为0.67 m的块状模型(土体模型),和直径0.025 mm、高度0.7 m的圆柱模型(试桩模型)，桩土模型如图10所示。土体采用Mohr-Coulomb模型，桩体采用isotropic elastic，用温度场模型(isotropic heat conduction)等效湿度场模型。土体周围四边，以及底部均约束三方向自由度，顶部不约束自由度。桩体和土体接触面采用FLAC3D内置的Coulomb滑动模型。

图10 桩土模型图Figure 10 Model of pile and soil

本次土体模型采用莫尔-库伦模型，材料参数体积模量K、剪切模量G，通过试验测得的土体力学参数弹性模量E运用式(15)、式(16)进行转换。模型参数选取如表1所示。

(15)

(16)

桩体与土体之间选取FLAC3D内置的interface接触模型，接触面参数法向刚度kn和切向刚度ks按式(17)确定。接触面参数取值如表2所示。

(17)

式中:Δzmin为接触面周边单元体的最小法向宽度。

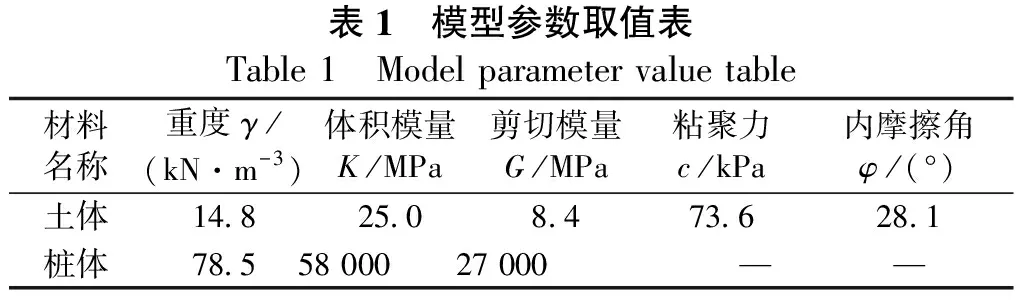
表1 模型参数取值表Table 1 Model parameter value table材料名称重度γ/(kN·m-3)体积模量K/MPa剪切模量G/MPa粘聚力c/kPa内摩擦角φ/(°)土体14.825.08.473.628.1桩体78.558 00027 000 ——

表2 接触面参数取值表Table 2 Contact surface parameter value table桩土界面类型法向刚度kn/(MPa·m-1)切向刚度ks/(MPa·m-1)粘聚力c/kPa内摩擦角φ/(°)接触侧面1.958×1071.958×10755.618.08接触底面1.958×1051.958×10535.612.08

5.2 计算结果及分析

通过数值模拟得到试验桩在各级荷载下的沉降量模拟值，模拟值与模型试验测量值荷载与桩顶沉降关系曲线如图11、图12所示。可以看出，模拟值与模型试验测量值的桩顶位移均随着荷载的施加而逐渐增大，表明数值模拟得到的结果与试验测试值高度吻合，变化规律一致，验证了数值模拟的可靠性。

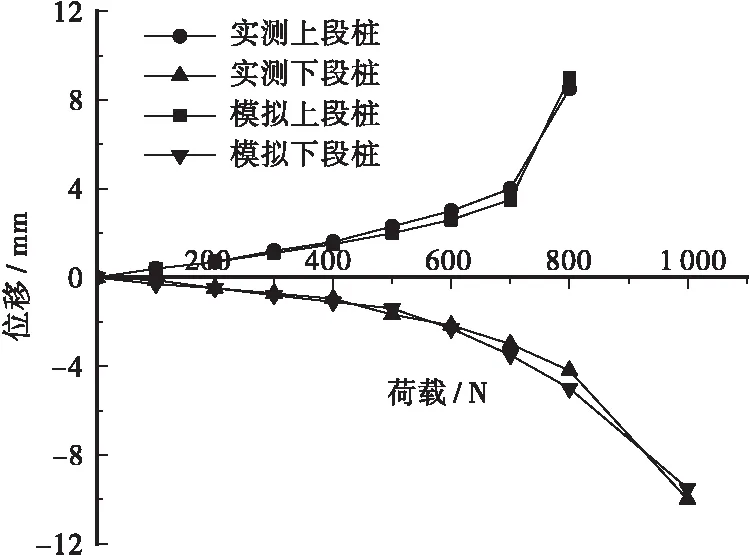
图11 自平衡试桩模拟与实测曲线Figure 11 Simulated and measured curves of self-balancing test pile

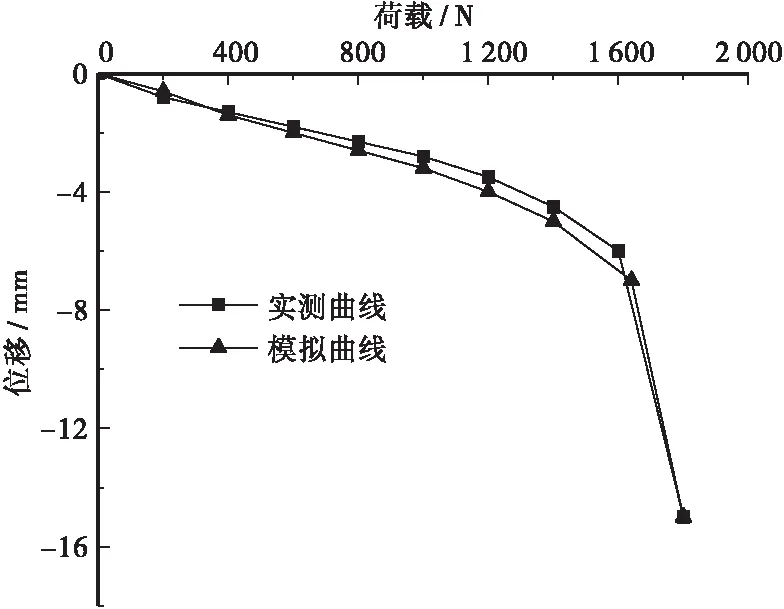
图12 传统静压桩模拟与实测曲线Figure 12 Traditional static pile simulation and measured curve

通过模型试验仅得到膨胀土含水率为18%(初始含水率)和30%(饱和含水率)的试验结果，不能完整分析含水率与负摩阻力取值间的关系。故采用FLAC3D模拟膨胀土在20%、22%、24%、26%、28%含水率下的负摩阻力取值，根据取值分布关系得到含水率与负摩阻力转换系数取值间的关系呈二次项分布如图13所示，负摩阻力转换系数取值随含水率的增大而呈减小趋势，相关系数R2=0.977 1，这表明膨胀土含水率对负摩阻力转换系数取值影响较大。