滨海吹填砂地层盾构纵坡掘进被动支护压力计算方法研究
2022-06-07胡艳峰钱伟丰
胡艳峰, 钱伟丰, 黄 明, 路 遥
(1.中交一公局厦门工程有限公司, 福建 厦门 361021; 2.福州大学 土木工程学院, 福建 福州 350108)
0 引言
隧道工程作为地下空间开发的重要手段,其在推进国家战略中扮演着极为重要的角色[1]。土压平衡盾构(EPB)目前已成为我国当前修建地铁隧道的主要方法之一[2]。土压平衡盾构通过维持土仓中的压力来平衡刀盘外部的水土压力,从而保证盾构掘进过程中开挖面的稳定[3]。
在我国东南滨海地区,大量海相淤泥场地通过吹填、预压和换填处理成为建设用地,而厦门市轨道交通3号线双沪站-空港经济区站穿越滨海吹填砂地层,该施工场地覆盖有大面积大厚度的吹填砂。不同于黏性土地层,盾构机在砂土地层掘进施工期间,由于土体黏聚力微弱,颗粒间的黏结程度很低,极易导致开挖面发生被动破坏,地表产生隆起,且这个破坏过程的时间历程极短。当盾构穿越滨海吹填砂地层时,掘进路线多表现为沿纵向上下坡方向。因此,盾构机在穿越滨海吹填砂地层掘进期间的纵向坡度对于开挖面稳定性的影响至关重要。
盾构纵坡掘进开挖面的被动稳定性问题是直接涉及工程质量与安全的重大技术难题,且目前施工尚无可靠的工程经验可供参考。所以,在滨海吹填砂地层中维持纵坡盾构隧道开挖面的稳定性、减小施工难度与施工风险,在确保安全的前提下合理地控制工程投资,是滨海吹填砂地层盾构隧道设计的一大关键技术。
目前,国内外许多学者对盾构隧道开挖面的被动稳定性进行了研究。LECA和DORMIEUX[4]等在基于上限法引入了二维锥形模型,采用上限法预测开挖面被动破坏时的极限支护压力。SOUBRA[5-6]将上述模型改进为沿滑动面的多块体模型,以研究隧道开挖面的被动稳定性。MOLLON[7-8]等提出了刚体平动和旋转破坏机制模型,使用空间离散技术来研究圆形隧道全断面的失稳破坏。吕玺琳[9]等通过开展离心模型试验,对干粉砂和饱和粉砂中盾构隧道开挖面的失稳特性和极限支护压力进行了研究,获得了支护压力与开挖面位移间的关系曲线、开挖面达到主动极限平衡状态时的破坏模式。ZHANG[10]等基于FLAC3D的模拟结果,改进了组合型截锥体模型以适用于摩擦-黏聚型土层条件下盾构开挖面支护压力的计算。梁禹[11]等结合河漫滩的地层特点,分析了迎坡条件下的富水砂层泥水平衡盾构开挖面主动极限支护压力的变化情况。
综上所述,尽管部分学者在考虑纵向坡度的条件下取得了一定的研究成果,但是在工程实践中,盾构隧道的纵向坡度对开挖面被动稳定性的影响往往被忽略,而关于滨海吹填地层盾构纵坡掘进对开挖面被动稳定性的分析研究更少。因此本文以厦门地铁3号线双沪站-空港经济区站盾构区间为背景,结合滨海吹填砂地层的特性,建立了有限元分析模型来模拟盾构纵坡隧道开挖面的被动破坏模式;基于极限分析的上限法,推导了考虑盾构纵坡掘进和支护压力沿开挖面高度呈梯形分布条件下,隧道开挖面被动稳定性的修正算法,并引入前人的计算结果和数值模拟结果对本文理论进行合理性验证。该研究结论为滨海吹填砂地层盾构纵坡掘进维持隧道开挖面的被动稳定性奠定了理论基础,可为今后类似工况的盾构隧道的设计与施工提供借鉴与参考。
1 工程背景
厦门市轨道交通3号线工程为厦门轨道交通线网当中的西南-东北向骨干线。3号线工程起自厦门火车站,终于翔安机场,线路全长38.47 km。其中线路有一段沿翔安东路西侧绿化带并行大嶝大桥跨过大嶝海域后进入大嶝岛区域,沿迎宾大道西侧绿化带向南敷设;过双沪村后,线路逐渐由高架转为地下敷设,直至终点翔安机场站。双沪站-空港经济区站这个区间需要穿越滨海吹填堆积区,其施工场地地质条件较为复杂,为滨海吹填造陆区域,该区域内分布有大面积的吹填砂;而对于盾构掘进需要穿越滨海区域浅海海底的隧道,盾构掘进将自上而下进行施工,此时盾构隧道将不可避免地产生一定程度的纵向坡度,如图1所示。

图1 工程位置与地质剖面图Figure 1 Project location and geological profile
由图1可知,盾构始发段和到达段线型略微倾斜,以维持盾构隧道拱顶上存在方较厚的覆盖土层,同时在掘进过程中,必须不断调整泥土仓内的支护压力以抵抗刀盘前方不断变化的水土压力。由于盾构隧道主要穿越的地层为吹填砂和淤泥混砂地层,且盾构掘进的始发段和到达段均存在隧道倾角,如图1中红色区域所示。盾构直径D约为6.3m,拱顶上方覆土厚度约为5.8~11.3 m,在盾构到达段覆盖土层厚度的突然下降使盾构刀盘前方的水土压力大幅度降低,如果土仓内的支护压力控制不好,可能会产生开挖面的被动失稳破坏,但是到达段区域主要穿越吹填砂地层,因此以该盾构掘进穿越吹填砂地层作为本文的主要分析对象。
2 数值模拟
2.1 模型的建立
Optum G2是一款专门用于岩土工程的有限元分析和极限分析软件(FEM)。它拥有网格自适应功能,能够定位剪应变较大的区域并自动加密网格,收敛性强。在复杂地质条件、复杂支护结构的破坏模式分析、地基承载力分析、可靠度分析等方面具有独特的优势。在实际工程中,隧道的纵向坡度δ通常在设计阶段控制在5°以内,然而在实际施工中,由于地质条件的复杂性和盾构机姿态控制的不确定性,盾构机的纵向坡度可能会超过设计值,因此本文采用周峻[12]等总结的结果可知,盾构机的最大纵向坡度约为10°。
为模拟上述存在纵向坡度的盾构隧道工程,采用Optum G2有限元极限分析软件,根据模型参数建立有限元分析模型,分别模拟盾构始发段和到达段的工况,如图2(a)、图2(b)所示。模型尺寸60m×50 m,模型中盾构隧道直径D=6 m且令C/D=1,其中隧道纵向坡度分别为δ=±10°,模型底部边界采用位移边界条件限制切向和法向2个方向的位移,模型左右两侧边界限制法向位移,模型顶端视为自由边界,同时盾构隧道拱顶和仰拱处的边界限制其法向位移,盾构隧道所穿越的吹填砂采用Mohr-Coulomb本构模拟,土体的主要参数如下:土体重度γ为 21 kN/m3,粘聚力c为 0 kPa,内摩擦角φ为23°,杨氏模量E为30 MPa,泊松比μ为0.3。
模型初始地应力采用模型初始地应力采用K0过程模拟,土体在自重作用下固结稳定。分析类型选择极限分析,单元类型选用上限单元,单元数量3 000。重置位移为0,以应变为控制变量进行3次自适应迭代计算,优化后的自适应网格后的网格数量与单元数量一致,如图2(c)、图2(d)所示。通过给予盾构隧道开挖面一定的可变荷载,使得开挖面前方土体达到被动破坏极限状态,最后截取模拟结果中开挖面前方土体的位移场和速度场云图进行比较分析。
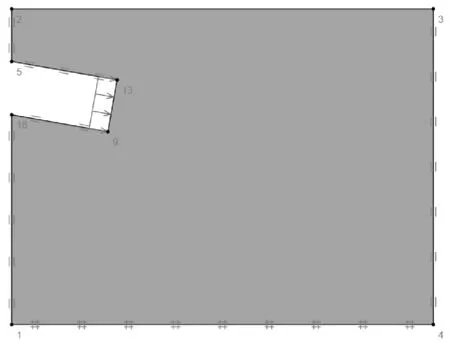
( a ) 始发段δ =-10°
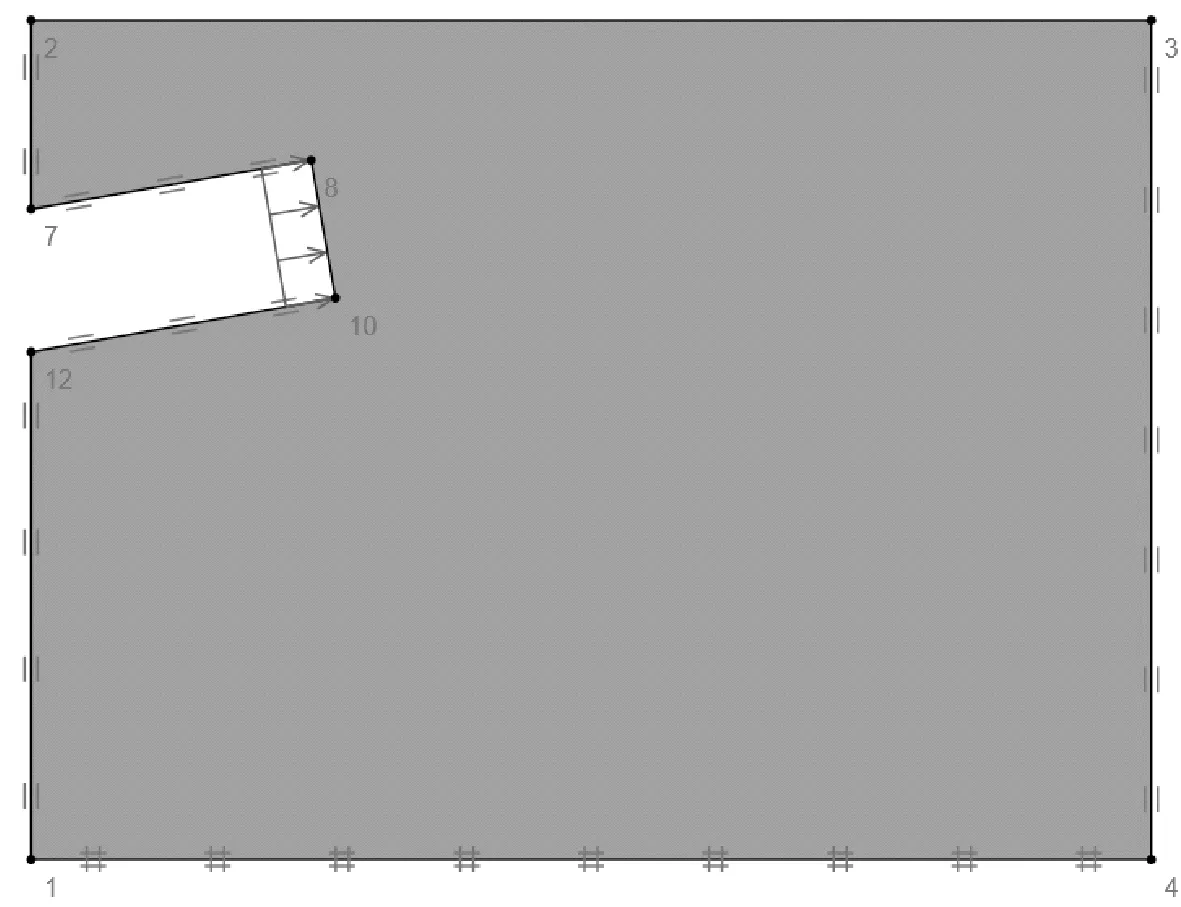
( b )到达段δ=10°
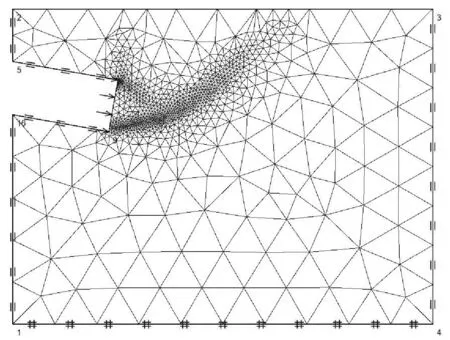
( c ) 始发段δ=-10°

( d )到达段δ=10°
2.2 结果分析
图3展示了有限元模拟结果的位移场和速度场,可以看出在整个模拟过程中,盾构隧道开挖面位移场和速度场向地表逐渐延伸,并露出地表,同时位移场的边界形成2条主要剪切带。其中1条剪切带由隧道仰拱处开始发展,沿弯曲线扩展至隧道顶部,并最终延伸至地表;另一条剪切带源起于隧道开挖面的仰拱处,且直接朝地表延伸。盾构隧道开挖面失稳区边界可近似为2条对数螺旋线线的轨迹组成,并进一步沿着近似垂直的方向由隧道拱顶延伸至地表。因此通过有限元计算结果,可以将盾构隧道开挖面被动破坏模式描绘成如图4所示的情况。

( a ) 始发段位移场

( b )到达段位移场
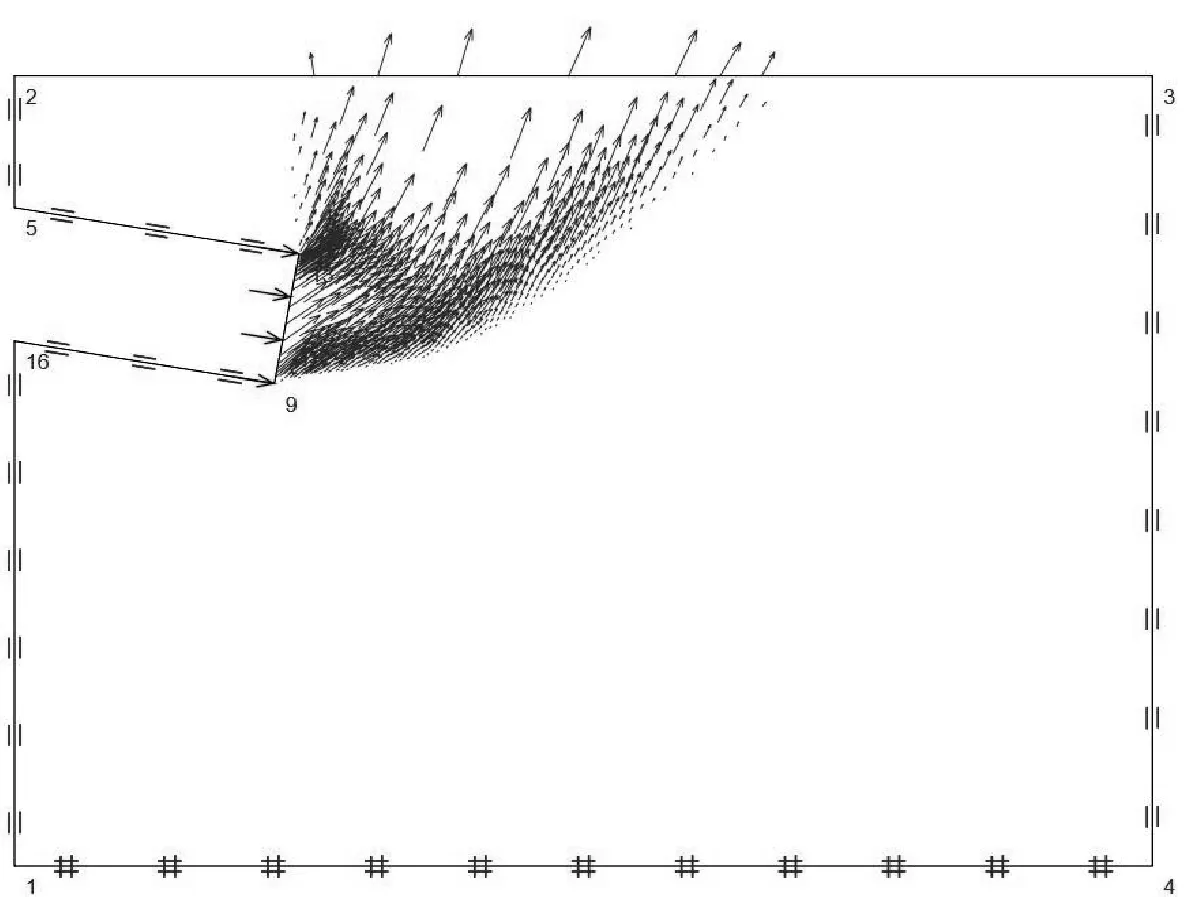
( c ) 始发段速度场
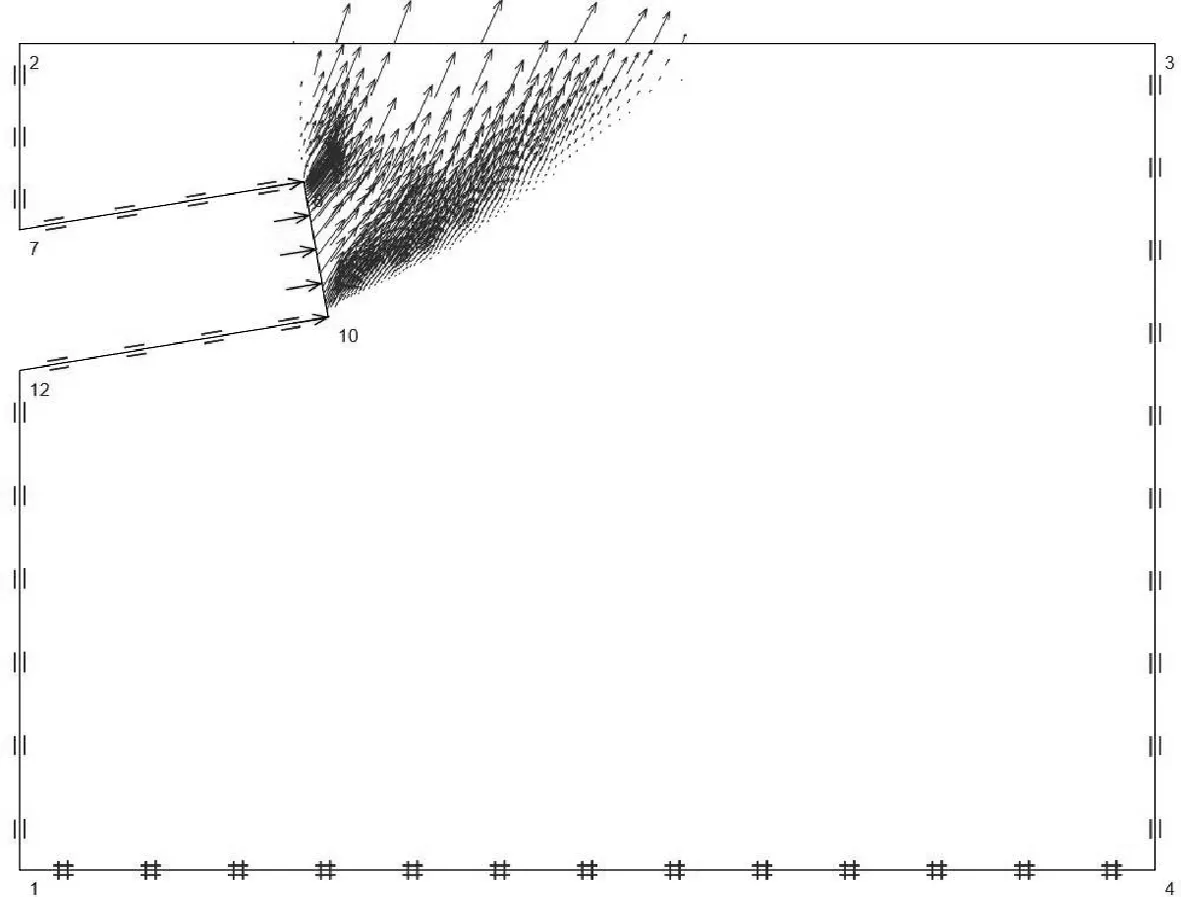
( d )到达段速度场
相比于物理模型试验,有限元方法能够高效便捷地模拟各种工况,如图4所示的开挖面被动破坏模式可以认为是适用于盾构隧道纵坡掘进的工况。为了更加高效地拓展研究深度,将基于有限元方法所产生的被动破坏模式,通过理论解析的方式进行研究。
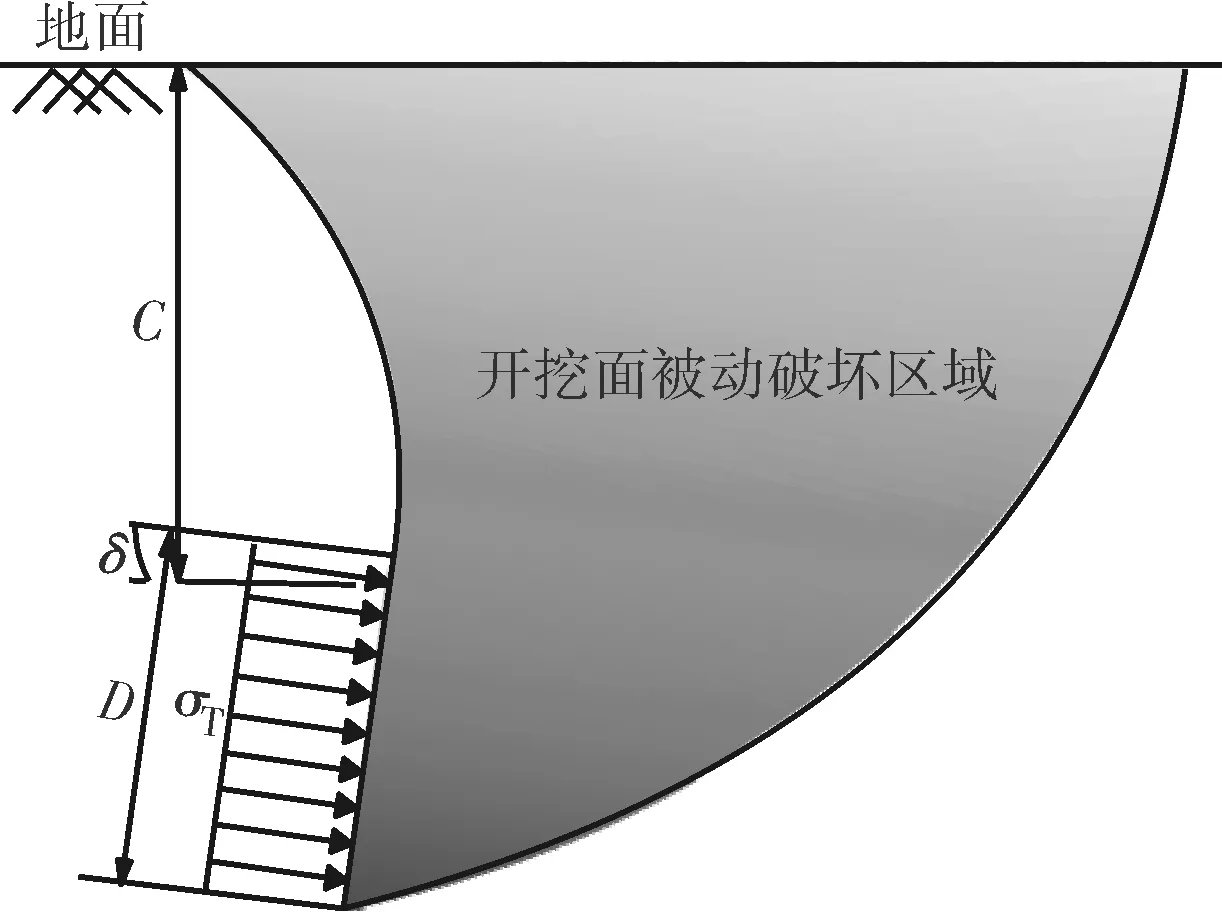
( a ) 俯角隧道δ<0°

( b )仰角隧道δ>0°
3 开挖面被动稳定性分析的上限解
3.1 开挖面上的支护压力
图5为均质土层中泥水盾构掘进过程中的开挖面支护压力分布。其中,盾构隧道直径为D;盾构隧道拱顶上方土层的覆盖厚度为C,将其用盾构隧道直径D进行归一化处理,则可定义无量纲参数C/D为埋深比。地面上可能存在的地表超载为σs;假定地下水位处于地面,地下水位到隧道拱顶的距离为H。土体的单位有效重度可表示为γ′;水的单位重度可表示为γw。如图5所示,土压平衡盾构机内土仓压力呈梯形分布,且随深度增加线性增加,其增加的速率即为仓内泥水的重度γF。梯形支护压力σT分为2部分:矩形部分σ1和三角形部分。其中在深度z处,开挖面上的总支护压力为:
σT=σ1+γFz
(1)
有效支护压力为:
σT′=σ1+(γF-γw)z-γwH
(2)

图5 盾构隧道开挖面上的土水压力分布Figure 5 Distribution of earth water pressure on the tunnel face
在实际盾构施工过程中,若盾构隧道直径较大,开挖面上分布的梯形荷载对被动破坏模式的影响较大;但是一般的盾构隧道直径通常取6 m左右,这种梯形荷载的影响往往被忽略,因此本文将考虑这种梯形荷载作用在盾构隧道开挖面上对被动稳定性的影响。
3.2 破坏机制的几何性质
通过极限分析法评估作用在盾构隧道开挖面上的被动极限支护压力,上限法根据考虑运动容许机构来求解极限支护压力,其中整个破坏机制的外部荷载的功率Pe应等于机制内部耗散的功率Pv(Pe=Pv)。本文在MOLLON[7-8]等建立的破坏机制的基础上,提出了无黏性土开挖面局部被动破坏机制。土体的物理力学行为采用Mohr-Coulomb屈服准则的塑性本构关系模型,并根据相关联流动法则来定义土体的破坏条件。土体的抗剪强度可分别通过有效黏聚力c′和有效摩擦角φ′来表示。根据相关联流动法则,在任意一种破坏机制中,速度方向必须与任意破坏面上的外法线方向成π/2+φ′。
图6即为本文提出的破坏机制,且假定为刚性块体在平面应变条件下的转动,同时以垂直于平面yoz坐标系的尺寸为单位。如图6所示,盾构掘进
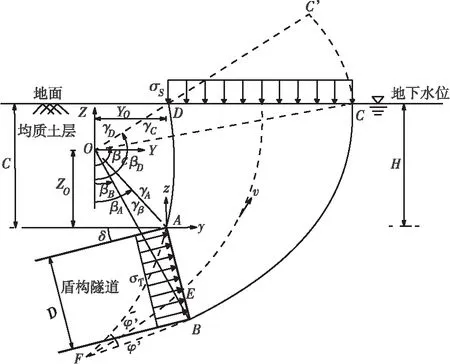
图6 盾构隧道开挖面的局部被动破坏机制Figure 6 Passive failure mechanism of tunnel face
工作面前方土体的破坏区域由2条对数螺旋(AD、BC)组成,点O是对数螺旋线的中心,AB的长度可以被认为是局部被动破坏区域的高度。为了表示AD和BC这2条对数螺旋线的方程,需要以O(YO,ZO)点为极点建立另一套极坐标系(β,r),于是极坐标下的对数螺旋AD和BC方程如下所示:
AD:r1(β)=rA·e(βA-β)·tan φ′
(3)
BC:r2(β)=rB·e(β-βB)·tan φ′
(4)
由图6可知,A点为直角坐标系yoz的原点,而O点在直角坐标系yoz中的位置为(YO,ZO),因此根据几何关系则有:

(5)
{βA=arctan(YO/ZO)
βB=arctan[YO/(ZO+D)]
(6)
然而,盾构隧道存在纵向坡度,因此需要对直角坐标系yoz进行旋转,若盾构隧道存在纵向仰角时,则直角坐标系yoz旋转δ;若盾构隧道存在纵向俯角时,则直角坐标系yoz旋转-δ,其计算公式如式(7)所示。
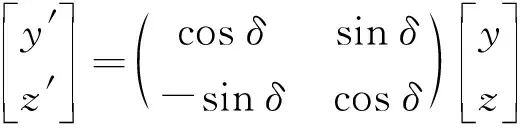
(7)
将式(7)带入式(5)、式(6)中,可得:
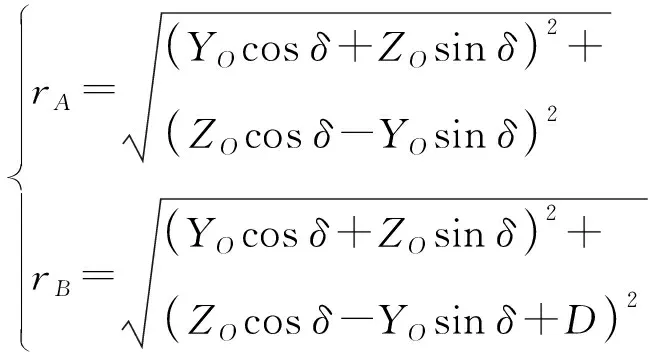
(8)
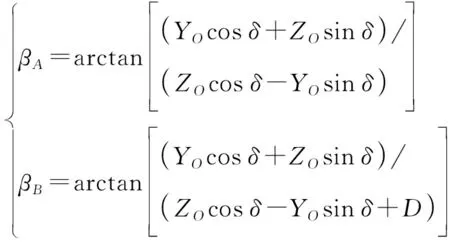
(9)
如图6所示,线段OA和OB长度分别为rA和rB,与z轴负方向的夹角分别为βA和βB,A、B、C、D这4个点的极坐标可分别表示为(βA,rA)(βB,rB)(βC,rC)(βD,rD),且D点与C′点共线,则C、D点的极坐标可通过式(3)、式(4)来表示:

(10)
在直角坐标系yoz中,由于C点和D点都位于地面的水平直线上,根据几何关系则有:
C-(ZOcosδ-YOsinδ)=rCcos(π-βC)=
rDcos(π-βD)
(11)
由式(3)~式(11)可知A、B、C、D这4个点的极坐标参数均可以通过O(YO,ZO)点的直角坐标参数来反映。由于本文考虑平面内的旋转速度场,这意味着整个破坏机制都以均匀的角速度ω围绕O点旋转,当盾构开挖面前方的土体发生被动破坏时,可以认为破坏区ABCD转动的角速度为ω,则有vA=ωrA,vB=ωrB。
3.3 极限支护压力的求解
为了计算被动局部破坏时的开挖面极限支护压力,需要分别计算外部荷载的功率Pe以及内部耗散的功率Pv,其中外部荷载的功率Pe主要由3部分组成:土体重力的功率Pγ,开挖面上支护压力σT′的功率PT,地面可能存在超载σs的功率PS。为了简便起见,将开挖面前方土体的破坏区域分为4部分:OBC′、OAD、OAB、CDC′。OBC′和OAB的计算区域如图7所示。
首先计算OBC′区域的重力功率,在此区域中取一段无穷小面积dS。如图7(a)所示,无穷小面积可以表示为:
(12)
在OBC′区域中,假设H点是无穷小面积的重心。则H点的速度可以表示为:
(13)
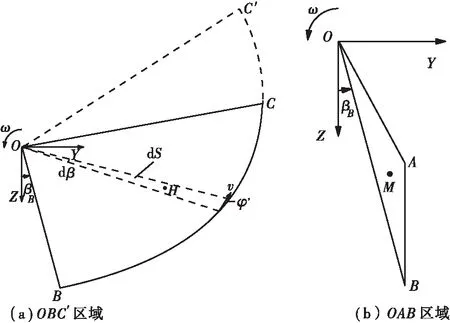
图7 计算区域的分解Figure 7 Decomposition of calculation region
因此,无穷小面积的重力功率计算可由下式来表示:
(14)
由于D点与C′点共线,则有βC′=βD。将式(12)、式(13)代入式(14)中,可得OBC′区域的重力功率:
(15)
将式(4)代入式(15)中,则OBC′区域的重力功率的表达式如下所示:
(16)
其中,f1(βA,βB)=
(17)
同理可得,OAD区域的重力功率表达式为:
(18)
其中,f2(βA,βB)=
(19)
对于OAB区域的重力功率的计算,如图7(b)所示,OAB区域的面积为SOAB其重心为点M,则令OAB区域的土体重力为γ·SOAB,M点的线速度为v=ω·OM。于是将OAB区域土体的重力与M点的线速度在重力方向上的投影相乘,即可得OAB区域的重力功率,其表达式如式(20)所示。
(20)
根据几何关系,则有:
(21)
CDC′区域土体重力的功率可分为OCD区域和OCC′区域这2部分计算,同理OCD区域土体重力的功率可表示为:
(22)
而OCC′区域土体重力的功率可表示为:
(23)
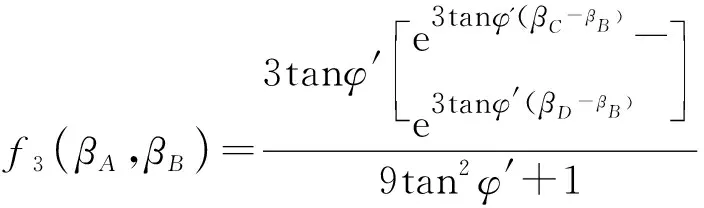
(24)
因此,CDC′区域土体的重力功率,其表达式如式(25)所示。
PγCDC′=PγOCC′-PγOCD
(25)
综上所述,联立式(13)、式(15)、式(19)、式(23),可得土体重力的功率的表达式:
Pγ=PγOBC′-PγOAD-PγOAB-PγCDC′
(26)
其次,计算作用在开挖面AB上的支护压力σT′的功率PT,而对于盾构掘进过程中施加在开挖面上的支护压力,本文视为大小如式(2)所示的梯形荷载,从而推导可得支护压力的功率PT如下所示:
(27)
经过化简可得:
PT=(σ1+γFD/2)Dω×
(YOcosδ+ZOsinδ)2f4(βA,βB)
(28)

(29)
然后计算地面可能存在超载σs的功率PS,如式(30)所示。
[(rC-rD)+2(C-ZO)tanφ′]
(30)
最后计算其内部耗散的功率Pv,功率的耗散发生在速度不连续的AD和BC处。螺旋线AD段的耗散功率为:
(31)
将式(3)代入式(31)中,则AD段的耗散功率可改写为:
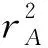
(32)
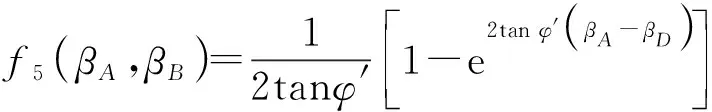
(33)
同理,BC段的耗散功率可以表示为:
(34)
将式(4)代入式(32)中,则BC段的耗散功率可改写为:
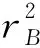
(35)
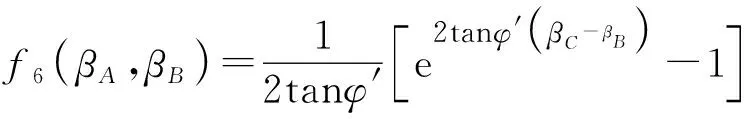
(36)
综上所述,开挖面前方失稳破坏区土体的耗散功率Pv如式(37)所示。
Pv=PvAD+PvBC
(37)
根据极限分析的上限法,当外部荷载的功率和内部耗散的功率相等时(Pe=Pv),所得到的极限支护压力即为上限解。联立式(8)、式(9)、式(26)、式(28)、式(30)、式(34),则极限支承压力可由以下公式求得:
σ1=γ′DNγ+σSNS+c'Nc-
(γF-γw)D/2+γwH
(38)
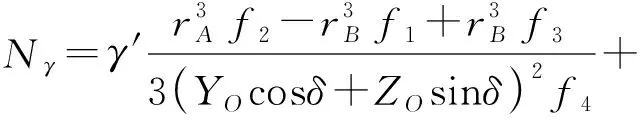
(39)
NS=
(40)
(41)
由上式可知,当盾构开挖面发生局部被动破坏时,其极限支护压力与参数YO、ZO,以及隧道纵向坡度δ有关。当参数c′、φ′、γ′、C/D均为已知时,无量纲系数Nγ、NS和Nc是YO、ZO和δ的函数。在相应的约束条件式(42)下,通过Matlab软件搜索YO,ZO,δ的最优值,得到最小的开挖面支护压力,该压力即为极限支护压力。
(YO>0
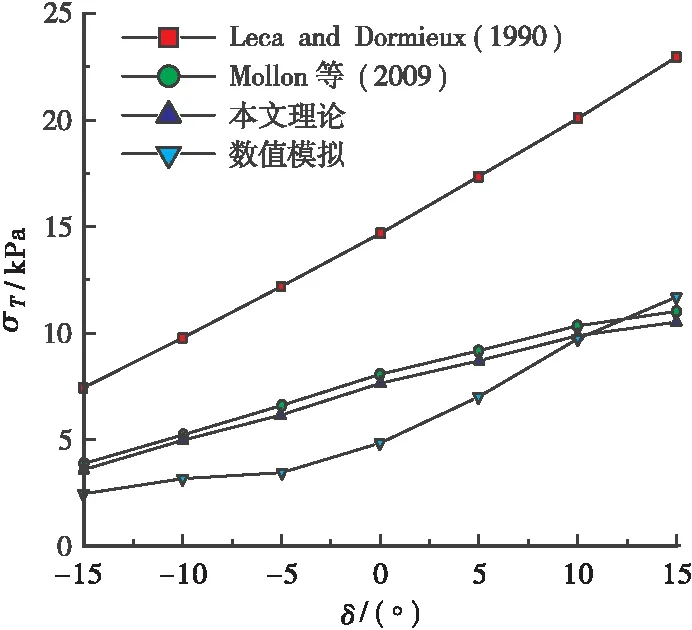
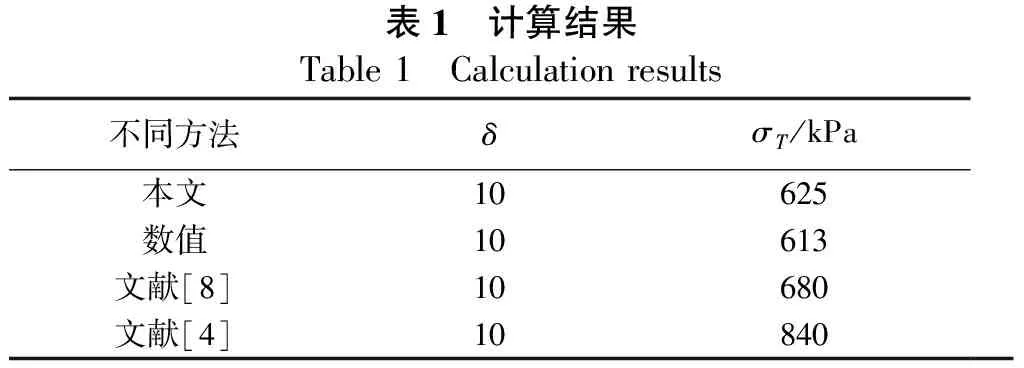
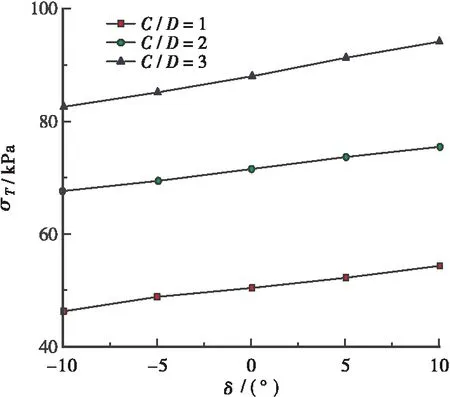
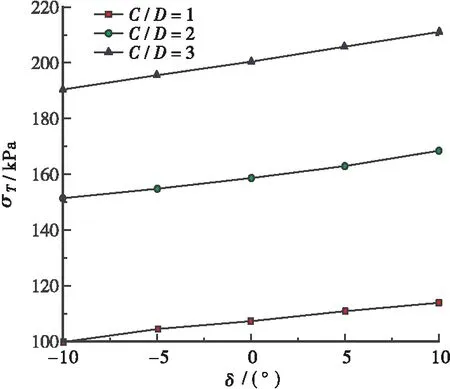
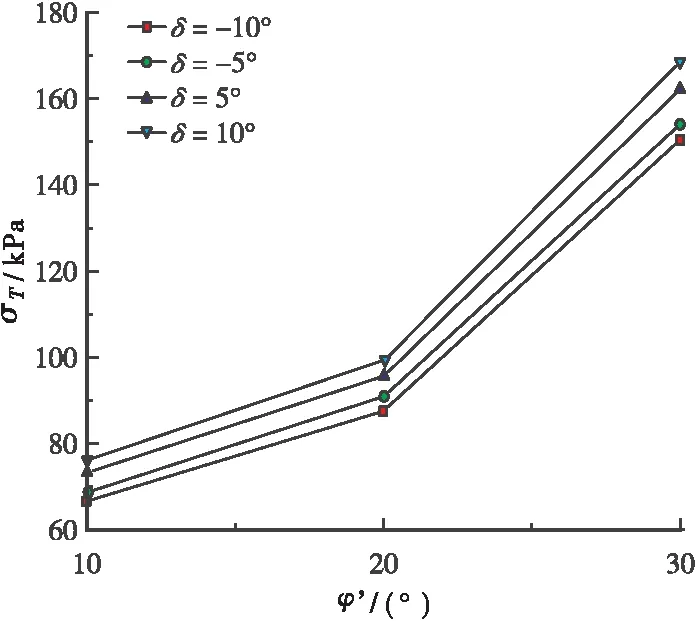
0 0<δ<π/2 (42) 将本文提出的理论解析的解与LECA和DORMIEUX[4]等,以及MOLLON[8]等提出的解析解分别进行比较,文献[4]和文献[8]都通过极限分析上限法求解开挖面的被动极限支护压力,二者均假设破坏区域起源于盾构隧道仰拱处。因此本文将以吹填砂为例开展对比分析,其土层物理力学参数与数值模型中的一致,不同理论解所求得的开挖面极限支护压力与数值模拟的结果如图8所示。 图8 不同理论解与数值模拟结果对比Figure 8 Comparison of different theoretical solutions and numerical results 由图8所示,不论哪一种极限分析理论,其开挖面的极限支护压力σT随着隧道由俯角倾斜变化至仰角倾斜过程中逐渐增大,且增长趋势近似为线性增加。其中,相比于其它极限分析理论(文献[4]和文献[8]),本文所提出理论的计算结果显然具有更高的保守性,其增加幅度也有显著提升,同时与文献[8]的计算结果较为接近,因此可以认为本文提出的理论合理有效。在δ<0°情形下,本文的计算结果约为数值模拟结果的1.5~2.0倍,文献[4]的计算结果约为数值模拟结果的3.0~3.5倍;而在δ>0°情形下,本文的计算结果下降至约为数值模拟结果的2.0~2.5倍,因此文献[8]不考虑隧道纵向坡度的计算,结果出现了近似等于或略小于数值模拟结果的情况,由此可知,盾构隧道纵向仰角的逐渐增大会降低理论模型的保守性,甚至出现预测值安全储备不足的情况,因而在应用中需要格外注意。 根据2.1中所示的土体物理力学参数可得最终计算结果,如表1所示。文献[4]和文献[8]所预测的极限支护压力分别为680 kPa和840 kPa,而根 表1 计算结果Table 1 Calculation results不同方法δσT/kPa本文10625数值10613文献[8]10680文献[4]10840 据本文所提出的方法预测的极限支护压力为625kPa,本文的计算结果均小于文献[4]和文献[8]的结果,同时数值模拟结果为613 kPa,本文所提出的极限支护压力计算结果比文献[4]和文献[8]的计算精度分别提高了8%和26%,表明文献[4]和文献[8]的方法均会高估开挖面的极限支护压力。而本文所提出的理论计算方法。根据本文所提出的方法预测的极限支护压力为625 kPa,与数值计算的结果(613 kPa)和文献[8]的计算结果(680 kPa)非常接近,不仅表明开挖面的失稳破坏均起源于盾构隧道的仰拱处,而且认为本文所提出的理论计算方法与数值模拟的结果更为吻合,具有一定的合理性。因此本文提出的方法所预测的极限支护压力相对较小,同时也可以获得与数值模拟基本一致的破坏模式。 不同有效内摩擦角条件下的δ-σT曲线如图9所示。随着盾构隧道纵向坡度的增大,维持开挖面稳定所需的极限支护压力显著增大,但增大速度基本相同。当有效内摩擦角较小(φ′=10°)时,开挖面极限支护压力的绝对增量较大,但相对增量较小;如果有效内摩擦角较大(φ′=30°),则结果相反。图9中不同有效内摩擦角(φ′=10°和φ′=30°)之间最大绝对增加量为105.6 kPa,最大相对增加量为55.2%。 不同有效内摩擦角对开挖面极限支护压力的影响如图10所示。如图10所示,在不同盾构隧道纵向坡度的条件下,极限支护压力随着有效内摩擦角的增大而增大,且不同倾角下极限支护力的变化趋势相似。这是因为土体的有效内摩擦角越大,土体颗粒表面的摩擦力越大,颗粒间的连锁效应产生了咬合力,有利于提高开挖面的极限支护压力以维持开挖面的被动稳定性。 在不同有效黏聚力值的条件下,开挖面极限支护压力随土体有效黏聚力的增大而增大,极限支护压力随纵向坡度的增大而线性增大;图11中不同有效内摩擦角(c′=10 kPa和c′=30 kPa)之间最大绝对增加量为6.8 kPa,最大相对增加量为 (a)φ′=10° (b)φ′=20° (c)φ′=30° 图10 有效内摩擦角对极限支护压力的影响(C/D=2)Figure 10 Effect of effective internal friction angle on ultimate support pressure 图11 不同有效粘聚力条件下开挖面所需的极限支护压力Figure 11 Ultimate support pressure required for excavation face under different effective cohesion conditions 本文以滨海吹填砂地层土压平衡盾构隧道开挖面为研究对象,综合采用数值模拟和理论分析的防范并结合工程实例,对土压平衡盾构纵坡掘进的隧道开挖面被动失稳机理展开了系统的研究,得出了以下结论: a.本文依托厦门市轨道交通3号线双沪站-空港经济区站工程,采用Optum 2G有限元极限分析软件对滨海吹填砂地层存在纵向坡度的盾构隧道开挖面的被动稳定性进行了数值模拟,并提出了适用于这种类似工况下的开挖面被动破坏模式,认为开挖面失稳区边界可近似为2条对数螺旋线的轨迹,并进一步由隧道拱顶延伸至地表。 b.基于数值模拟所得的结果,利用极限分析的上限法,建立了分析盾构掘进过程中的开挖面被动破坏机制,该机制不仅考虑了隧道纵向坡度的情况,还考虑了土仓内压力沿隧道开挖面呈梯形分布。并将本文提出的理论和数值的计算结果与现有理论所获得的极限支护压力进行比较,可以发现本文提出的理论在极限支护压力的计算方面与其它理论和数值模型吻合较好,且相比现有理论的计算精度分别提高了8%和26%,表明本文理论是有效且合理的。 c.盾构隧道开挖面的失稳破坏均起源于盾构隧道的仰拱处,其被动极限支护压力随纵向坡度的增大呈显著地线性增加趋势。当土体的有效内摩擦角增加67%时,开挖面极限支护压力增加17.9%;当土体的有效黏聚力增加67%时,开挖面极限支护压力增加10.4%,说明土体有效内摩擦角越大,纵向坡度对开挖面极限支护压力的影响越大,且内摩擦角的影响最为显著。因此可以认为纵向坡度变化影响被动极限支护压力主要是由土颗粒之间的摩擦力产生的。4 计算结果分析
4.1 极限支护压力的对比分析
4.2 极限支护压力的参数分析


5 结论
