独塔钢桁梁单索面斜拉桥地震响应参数分析

曾 勇，曾渝茼

(1.重庆交通大学 山区桥梁及隧道工程国家重点实验室,重庆 400074; 2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心,重庆 400074)

地震具有破坏力大、发生迅速和源发不可预测的特点，是桥梁可能会遭受的动力灾害之一。独塔钢桁梁单索面斜拉桥跨度大，并且经常因其造型优美成为城市的地标建筑。独塔钢桁梁单索面斜拉桥的非线性因素较多，地震响应复杂，进行非线性时程分析比反应谱分析更加科学，具有重大工程意义。

国内外学者对于斜拉桥地震响应参数分析做了许多研究，刘昊苏[2]等采用反应谱法研究了不同设计参数下矮塔斜拉桥抗震动力学，焦驰宇[3]等采用反应谱法分析了塔梁连接方式的参数变化对大跨度斜拉桥的地震作用的影响。他们研究的对象都为非线性因素复杂的特大桥，但采用的却是反应谱法这种线性的地震响应研究方法。阮怀圣[4]等虽然对5座大跨度公铁两用钢桁梁斜拉桥进行了地震响应特性研究，但却是通过动力特性进行地震响应分析，仍然具有局限性。文献[5-13]对其他桥型进行结构参数变换研究了桥梁抗震性能，说明结构参数变换研究桥梁地震响应具有一定的科学性。时程分析法是较为科学的一种研究桥梁地震响应的方法，但目前没有学者基于非线性时程分析对独塔钢桁梁单索面斜拉桥进行地震影响参数分析。

本文以西南某独塔钢桁梁单索面斜拉桥为研究对象，通过MIDAS/Civil建立多个不同结构参数的模型，变换不同的结构参数，包括斜拉索刚度变换、钢桁梁刚度变换、结构体系变换，采用非线性时程分析法分析其地震响应。桥型相同的桥梁通常在地震作用下的规律相似，因此独塔钢桁梁单索面斜拉桥地震响应参数分析，具有普遍意义，研究方法和结论可为同类型工程提供参考。

1 工程概况与有限元模型

1.1 工程概况

某独塔钢桁梁单索面斜拉桥(如图1所示)横跨嘉陵江，连接重庆市渝中区和江北区，跨径组合为(88+312+240+80) m，桥梁全长720 m。主梁为双层钢桁梁布置，上层为双向四车道的公路交通，下层为双向轨道交通，实现公轨两用。上层正交异形桥面板因功能需要宽度在24～37 m之间变化。桥塔为“天梭”造型，高度为182 m，采用C50混凝土材料。斜拉索下端锚间距为16 m，上端锚间距为3.4 m，单索面布置。桥梁设防等级为A类，当地基本地震烈度为Ⅵ度，桥梁地震设防烈度为Ⅶ度。

图1 某独塔钢桁梁单索面斜拉桥Figure 1 A single tower steel truss single cable plane cable stayed bridge

1.2 有限元模型

MIDAS有限元软件被用于建立桥梁的全桥模型，共12 806个节点，26 111个单元，单元数目合适且达到了足够的精度，对于桥梁各个构件的模拟准确。桥塔、辅助墩、临时墩采用梁单元模拟，钢桁梁的上弦杆、下弦杆、腹杆等均按梁单元模拟，正交异形桥面板采用板单元模拟，斜拉索采用桁架单元模拟。钢桁梁和斜拉索的刚度变化，通过改变对应材料的弹性模量模拟。采用非线性时程分析法进行地震响应分析，通过变换多种结构参数，观察不同结构参数对地震响应的影响。有限元模型见图2，主要材料见表1。

图2 有限元模型Figure 2 Finite element model

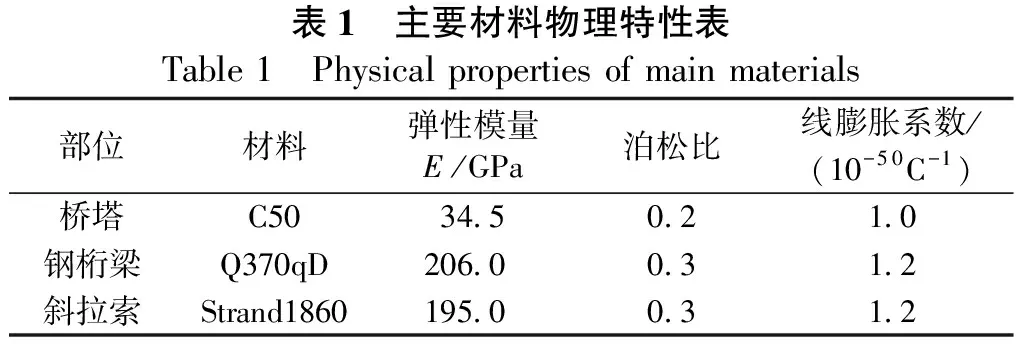
表1 主要材料物理特性表Table 1 Physical properties of main materials部位材料弹性模量E/GPa泊松比线膨胀系数/(10-50C-1)桥塔C5034.50.21.0钢桁梁Q370qD206.00.31.2斜拉索Strand1860195.00.31.2

2 地震波的选取和PGA调整

根据桥梁设防等级A类，场地类型Ⅱ类，基本地震烈度Ⅵ度，桥梁地震设防烈度Ⅶ度，选择具有代表性的地震波并进行加速度峰值调整对桥梁进行E2地震作用下的非线性时程分析，并设置为顺桥-横桥耦合向地震波。

输入国际常用的El Cento Site 270 Deg地震波，并通过PGA(加速度峰值)调整系数调整地震动加速度峰值，PGA调整系数计算公式如下：

(1)

式中：Ci为桥梁重要性系数，E2地震下的A类桥梁取1.7；Cs表示场地系数，场地类型为Ⅱ，抗震设防为6的桥梁取1.0；Cd表示阻尼调整系数，通常情况下取1.0；A表示水平向设计基本地震动加速度峰值，抗震设防烈度为Ⅵ度的桥梁，取0.05g；Pk为所选取的地震波加速度反应谱峰值。

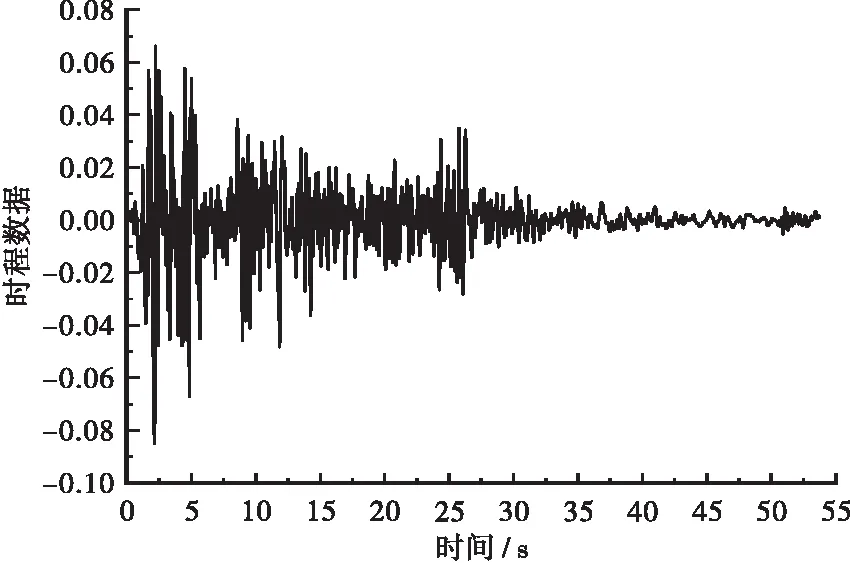
图3 调整过后的El-Cento地震波的时程函数Figure 3 Adjusted time history function of El-cento seismic wave

El Cento Site 270 Deg地震波下，PGA调整系数为：

0.238 2

加速度峰值调整后的时程函数见图3。

3 地震响应参数分析

3.1 斜拉索刚度变化对桥梁地震响应的影响

斜拉索刚度的变化通过改变斜拉索所用材料弹性模量的倍数变化模拟，其变换的倍数分别为：0.6、0.8、1.2、1.4、1.6倍。分析斜拉索刚度变化对顺桥-横桥耦合向地震作用下桥塔弯矩和位移，以及钢桁梁下弦杆轴力与位移的影响时，所有的数据均取地震作用下的最大值。不同倍数斜拉索刚度的桥梁在地震作用下桥塔位移U和弯矩My最大值沿塔高分布图见图4，不同倍数斜拉索刚度的桥梁在地震作用下钢桁梁右侧最外边下弦杆位移U和轴力Fx最大值沿桥面纵向分布图见图5。

(a) 地震作用下的桥塔位移U最大值沿塔高分布

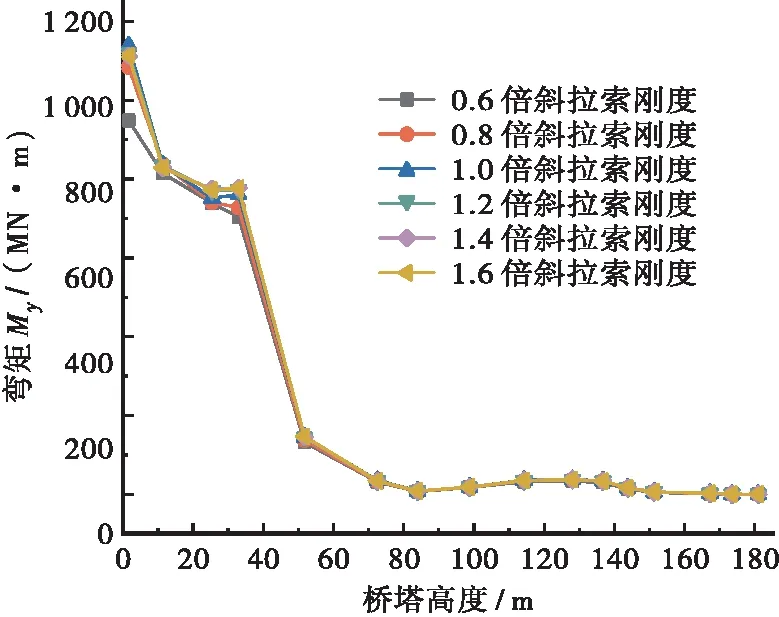
(b) 地震作用下的桥塔弯矩My最大值沿塔高分布

分析图4可知：

a.斜拉索刚度的变化对于地震作用下桥塔位移的影响主要集中在塔高高于100 m后，因为塔高在100 m后，塔的宽度逐渐收窄，对于地震作用将更加敏感，且更上面的141 m到172 m为拉索区，斜拉索刚度变化会引起拉索区刚度的变化；当桥塔高度大于100 m后，斜拉索刚度越大，桥塔在地震作用下的位移越小，因为斜拉索刚度增大，桥塔与斜拉索连接的部位刚度更大，从而减小塔高100 m以上的部位地震作用下的桥塔位移；塔高为182 m时，0.6倍斜拉索刚度时的桥塔在地震作用下的位移U最大，为0.086 1 m，1.6倍斜拉索刚度时的桥塔在地震作用下位移U最小，为0.056 5 m，降幅达34.4%。可见斜拉索刚度增大可以减小地震作用下的桥塔位移。选择一个刚度适当的钢材作为斜拉索，在保证柔性性能的条件下尽量增加刚度，可以减轻地震对桥塔位移的影响。

b.斜拉索刚度的变化对地震作用下的桥塔弯矩仅在桥塔高度小于40 m时有明显影响，且桥塔地震作用下弯矩My的大小并没有与斜拉索刚度大小有确定规律的关系，因为桥塔所受的地震力主要传递自桥墩和主梁，即使斜拉索刚度增加对桥塔所

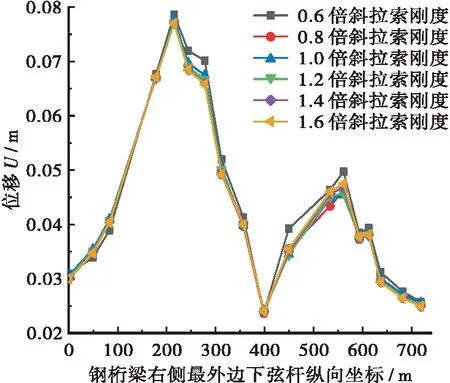
(a) 地震作用下的钢桁梁下弦杆位移U最大值沿桥面纵向分布

(b) 地震作用下的钢桁梁下弦杆轴力Fx最大值沿桥面纵向分布

受的地震力影响并不大。塔高为0 m，斜拉索刚度为0.6倍时桥塔在地震作用下的弯矩最小，1.0倍斜拉索刚度时桥塔在地震作用下的弯矩最大；塔高为37 m时，0.6倍斜拉索刚度时桥塔在地震作用下的弯矩最小，1.0、1.2、1.4、1.6倍斜拉索刚度时桥塔在地震作用下的弯矩十分接近。

分析图5可知：

a.桥面纵向坐标为400 m时，钢桁梁下弦杆的地震作用下位移U最小，因为此处为塔梁交界处，通常斜拉桥的塔梁交界处地震响应位移最小；斜拉索刚度变化对于钢桁梁在地震作用下的位移影响很小，图5(a)中的6条曲线分布较为集中。虽然斜拉索刚度增大会增加钢桁梁与斜拉索连接部位的刚度，但由于本桥的斜拉索布置形式为单索面稀索，斜拉索与钢桁梁连接的部位与全长720 m相比又过于局部，因此只要斜拉索刚度不过小，斜拉索刚度变化对钢桁梁地震作用下的位移影响就很小。

b.斜拉索刚度变化对于钢桁梁下弦杆在地震作用下的轴力Fx影响也不大，随着斜拉索刚度变化，钢桁梁下弦杆在地震作用下的轴力变化幅度并不大，即使在纵向坐标为400 m时(桥塔与钢桁梁交界处)，也只是0.6倍斜拉索刚度时的地震作用下轴力有轻微差异。

3.2 钢桁梁刚度变化对桥梁地震响应的影响

钢桁梁刚度的变化通过改变钢桁梁所用材料弹性模量的倍数模拟，其倍数变换分别为：0.6、0.8、1.2、1.4、1.6倍。分析钢桁梁刚度参数变化对顺桥-横桥耦合向地震作用下桥塔的弯矩和位移，以及钢桁梁下弦杆的轴力与位移的影响时，所有的数据均取自地震作用中的最大值。不同倍数钢桁梁刚度的桥梁在地震作用下桥塔位移U和弯矩My最大值沿塔高分布图见图6，不同倍数钢桁梁刚度的桥梁在地震作用下弦杆位移U和轴力Fx最大值沿桥面纵向分布图见图7。

分析图6可知：

a.钢桁梁刚度的变化对于桥塔在地震作用下位移U有较为明显的影响，塔高120 m以下时影响较小，塔高在120 m以上时影响较大，且塔高182 m时影响最大，随着钢桁梁刚度增大，桥塔在地震作用下位移减小，因为拉索区(141～172 m)桥塔地震作用下的位移受桥塔中下部和斜拉索两部分影响，当钢桁梁刚度增大时，斜拉索传递的地震作用减小的同时桥塔与钢桁梁连接的部位刚度增大；塔高为182 m时，0.6倍钢桁梁刚度时桥塔在

(a) 地震作用下的桥塔位移U最大值沿塔高分布

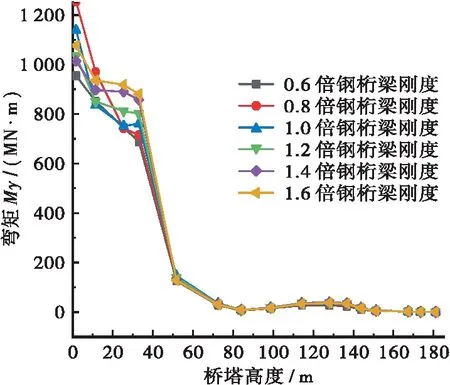
(b) 地震作用下的桥塔弯矩My最大值沿塔高分布

地震作用下位移最大，为0.085 m，1.6倍钢桁梁刚度时桥塔在地震作用下位移最小，为0.067 m，降幅约21.8%；可见，钢桁梁刚度的增加可以减小地震作用下的桥塔位移。

b.钢桁梁刚度的变化对于桥塔在地震作用下弯矩My的影响在40 m以下较为明显；在桥塔根部(桥塔高度为0 m时)，0.8倍钢桁梁刚度时的桥塔在地震作用下弯矩最大，但在桥塔高度为37 m时，0.8倍钢桁梁刚度时的桥塔在地震作用下弯矩最小，不同桥塔高度下，钢桁梁刚度的变化对于桥塔在地震作用下弯矩的影响并不一致。可见，钢桁梁刚度变化对于桥塔弯矩的影响的机理较为复杂，需要进一步研究。

分析图7可知：

a.钢桁梁刚度参数变化对钢桁梁下弦杆在地震作用下位移的影响主要集中在88～400 m之间，这是斜拉桥主跨的整个跨度，主跨跨度较大，地

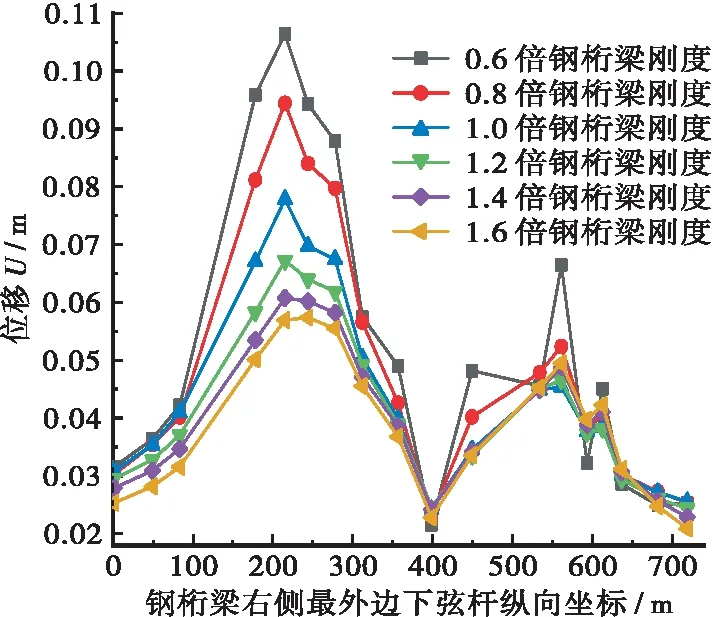
(a) 地震作用下的钢桁梁下弦杆位移U最大值沿桥面纵向分布

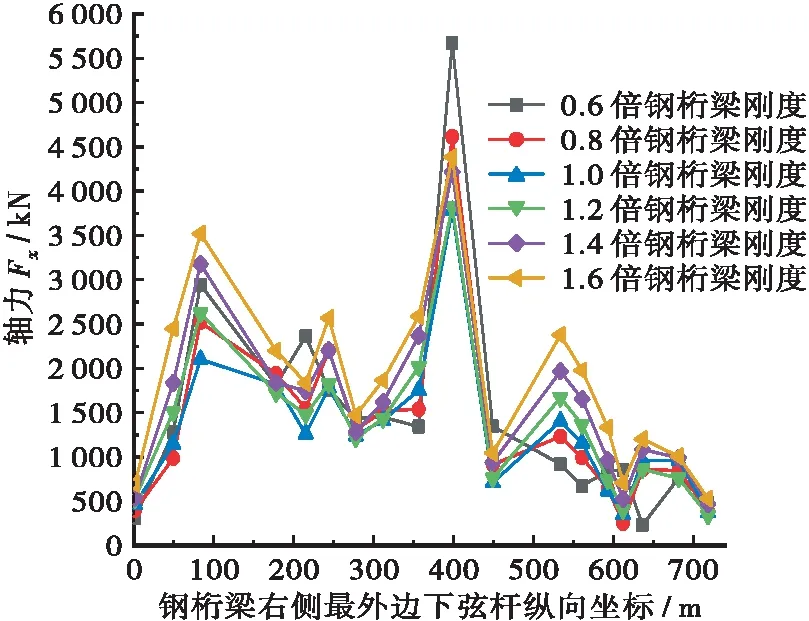
(b) 地震作用下的钢桁梁下弦杆轴力Fx最大值沿桥面纵向分布

震作用下的位移较为敏感；随着钢桁梁度倍数的增加，钢桁梁下弦杆在地震作用下的位移减小，因为钢桁梁是桥梁最主要的部件，当钢桁梁的刚度增加后，钢桁梁与桥塔连接处的刚度增加、位移减小，同时斜拉索所传递的地震作用下的位移也相对减少；当纵向坐标为244 m时(主跨跨中)，影响最明显，0.6倍钢桁梁刚度时钢桁梁下弦杆在地震作用下的位移最大，为0.048 m，1.6倍钢桁梁刚度时钢桁梁下弦杆在地震作用下的位移最小，为0.034 m，降幅为30.4%。可见，增加钢桁梁的刚度可以减小地震作用下钢桁梁的位移。

b.钢桁梁刚度变化对钢桁梁下弦杆在地震作用下的轴力影响较大，且轴力曲线在整个纵向坐标范围内均有波动，因为钢桁梁杆件之间相互连接，互相传递内力；纵向坐标为88 m时(主跨边墩处)，1.0倍钢桁梁刚度时钢桁梁下弦杆在地震作用下轴力最小，1.6倍钢桁梁刚度时钢桁梁下弦杆在地震作用下轴力最大，变化幅度为16.6%；当纵向坐标为400 m时(塔梁交界处)，1.0倍钢桁梁刚度时钢桁梁下弦杆在地震作用下轴力最小，0.6倍钢桁梁刚度时钢桁梁在地震作用下轴力最大，变化幅度为33.4%；不同纵向坐标下，钢桁梁刚度的变化对于钢桁梁下弦杆在地震作用下轴力的影响并不一致，没有统一规律。因为钢桁梁与钢箱梁不同，钢桁梁是由多种杆件组成，上弦杆、腹杆、下弦杆分布的位置不同，且各种杆件之间均有弯矩、轴力、位移等的传递，下弦杆并不是只和下弦杆连接，所以很难有统一的规律。

3.3 结构体系变化对桥梁地震响应的影响

将原结构的半漂浮体系参数分别变为：漂浮体系、刚构体系、塔梁固结体系。通过改变塔-梁的连接约束和桥墩处支承实现几种体系的转化，几种体系的结构示意图见图8。分析结构体系参数变化对顺桥-横桥耦合向地震作用下桥塔的弯矩My和位移U，以及钢桁梁下弦杆的轴力Fx与位移U的影响时，所有数据均取自地震动作用下的最大值。不同结构体系的桥梁在地震作用下桥塔位移U和弯矩My最大值沿塔高分布图见图9，不同结构体系的桥梁在地震作用下弦杆位移U和轴力Fx最大值沿桥面纵向分布图见图10。

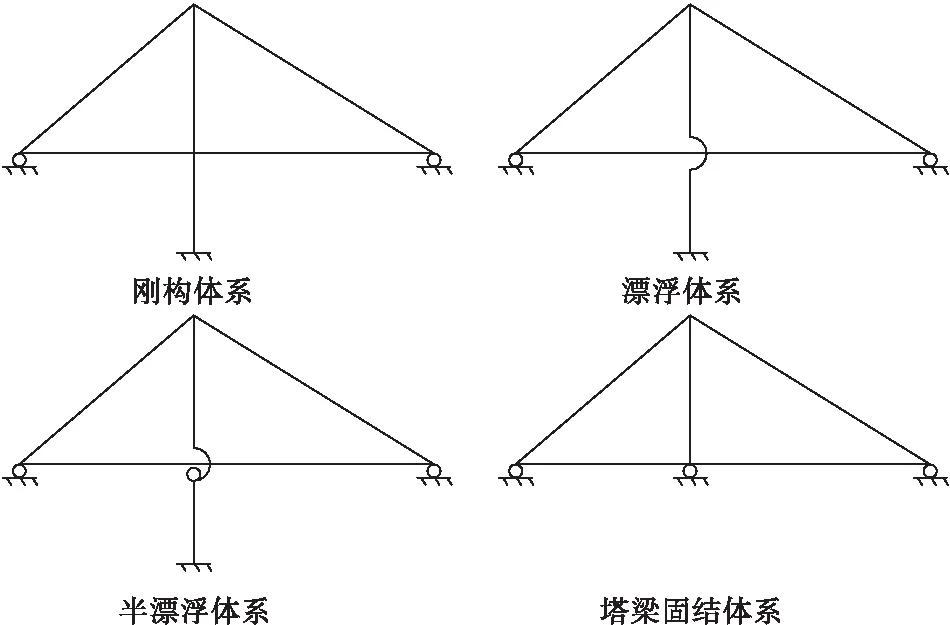
图8 独塔斜拉桥的几种体系Figure 8 Several systems of single tower cable stayed bridge

分析图9可知：

a.桥塔高度小于130 m时，漂浮体系在地震作用下的桥塔位移最小，但桥塔高度大于130 m时，漂浮体系在地震作用下的桥塔位移最大，因为漂浮体系的特点是塔-梁之间自由，桥塔高度在130 m以下时，桥塔更多只接受桥墩传递的地震作用，受主梁通过斜拉索的间接传递地震作用较小，而当塔高高于130 m时，桥塔地震作用受斜拉索影

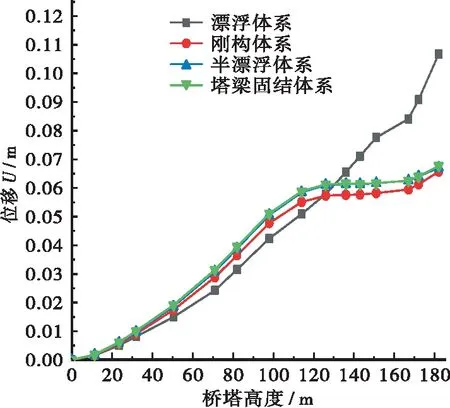
(a) 地震作用下的桥塔位移U最大值沿塔高分布

(b) 地震作用下的桥塔弯矩My最大值沿塔高分布

响更多，塔-梁仅通过斜拉索间接连接，增大了塔-梁之间地震作用的传递；除了漂浮体系，其余3种体系在地震作用下的桥塔位移较为接近，尤其是半漂浮体系和塔梁固结体系在地震作用下位移曲线几乎重合，且刚构体系在地震作用下位移最小，因为塔梁固结体系与半漂浮体系极为相似，而刚构体系使得整个桥梁的刚度变大。

b.漂浮体系在地震作用下桥塔弯矩最小，其余3种体系在地震作用下桥塔的弯矩非常接近，且分布规律一致。因为除漂浮体系外，它与3种体系的塔-梁之间均存在连接，塔-梁之间的连接会传递弯矩，使得桥塔地震作用下的弯矩被放大。

分析图10可知：

a.漂浮体系钢桁梁下弦杆在地震作用下的规律与其余3种体系不同。漂浮体系在地震作用下钢桁梁下弦杆的位移非常大，其余3种体系在地震作用下钢桁梁下弦杆的位移接近，其中刚构体系在地

(a) 地震作用下的钢桁梁下弦杆位移U最大值沿桥面纵向分布

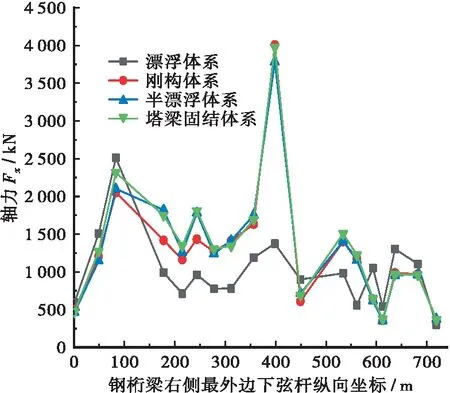
(b) 地震作用下的钢桁梁下弦杆轴力Fx最大值沿桥面纵向分布

震作用下的位移最小，因为塔-梁之间的连接可以减小地震作用下的位移，而漂浮体系的钢桁梁与桥塔之间没有连接，钢桁梁失去了桥塔的竖向支承使得钢桁梁位移很大，刚构体系整体刚度较大，钢桁梁的位移最小。

b.漂浮体系在地震作用下钢桁梁下弦杆的轴力分布规律与其余3种体系不同，其余3种体系在纵向坐标为400 m时在地震作用下的轴力出现了极值，而漂浮体系没有，因为漂浮体系的桥塔与主梁并没有设置连接，而400 m处正好是塔-梁连接处；漂浮体系钢桁梁下弦杆在地震作用下的轴力比其余3种体系小，而其余3种体系分布规律相同，且波动很小。

4 结论

桥型相同的桥梁通常在地震作用下的规律相似，独塔钢桁梁单索面斜拉桥地震响应参数分析具有普遍意义，可以为后续工程提供参考。本文利用非线性时程分析，变换不同的结构参数，研究了独塔钢桁梁单索面斜拉桥结构参数对地震响应的影响，得出以下结论：

a.当桥塔到达一定高度时，斜拉索刚度越大，桥塔在地震作用下的位移就越小，即：斜拉索刚度增大可以优化桥塔地震作用下的位移；斜拉索刚度变化对于地震作用下桥塔弯矩、钢桁梁位移与轴力的影响很小。

b.钢桁梁刚度的增加，可以使地震作用下桥塔和钢桁梁的位移减小，即：钢桁梁刚度增大可以优化桥塔和钢桁梁地震作用下的位移；钢桁梁刚度参数变化对地震作用下桥塔弯矩和钢桁梁下弦杆轴力的影响机理不明确，需要进一步更为细致的研究。c.漂浮体系总体来说地震作用下的位移大于其他3种体系，但地震作用下的内力明显小于其余3种体系；其余3种体系，从地震作用下桥塔和钢桁梁内力和位移的角度上来看，表现相似。