波浪力下小尺度圆柱群桩的内力与变形分析
2022-06-07胡春林孙帅康
胡春林, 孙帅康
(武汉理工大学 土木工程与建筑学院, 湖北 武汉 430070)
1 概述
波浪力是海洋等深水工程下部结构设计的控制荷载,群桩基础是此类工程中应用最为广泛的基础类型[1],波浪力作用下群桩基础的受力与响应问题一直受到广泛的关注。目前国内外在该领域的研究已有较多成果:刘逸敏[2]等分析了淹没承台时圆柱桩身所受波浪力的作用特性,并给出波浪力的计算方法。张力伟[3]等利用数值软件建立三维波浪水槽,在考虑波浪与桩基耦合的基础上计算了线性波浪作用下软土地基中圆柱桩所受波浪力的数值解。郐艳荣[4]等基于雷诺时均Navier-Stokes方程与标准k-ε湍流模型建立波浪水槽,研究了波浪入射角、KC数等参数对跨海大桥桩基所受波浪力的影响规律。徐博[5]等基于RANS和k-ω湍流方程,建立波浪和高桩承台的耦合模型,研究了承台所受各方向波浪力的变化规律、承台周围的流场,以及净空对波浪力的影响规律。张耀泽[6]基于线性波理论,建立三维波浪水槽和大柔度群桩基础模型,在考虑双向流固耦合的基础上,分析了群桩基础受到的波浪力,并将数值解与理论解进行比对分析,研究了桩基自身柔度对其受力的影响规律。WANG[7]等通过模型试验分析了作用于桩身的波浪力,并结合数值模型研究了桩身弯矩的分布规律。黄雯[8]等基于CFD理论,建立三维数值波浪水槽,研究了桩距、桩位置的变动对群桩中各基桩受力的影响规律。何海峰[9]等基于Morison方程计算桩身波浪力,研究了波浪力作用下几种不同结构形式群桩基础的受力特性。施勇[10]等通过物理模型试验,构建三桩基础风电机组结构的缩尺物理模型,系统研究了结构在规则波浪、不同方向的入射波浪和随机波浪作用下的动力响应。唐云[11]等通过物理模型试验,研究了低桩承台直立堤在不规则波浪作用下波浪力的变化规律。综合现有文献,可以看出目前相关研究多侧重于波浪力的求解与作用特性,而对波浪力作用下桩基的动力响应研究相对较少且主要围绕整个上下部结构的响应展开,对桩基的内力变化、分布规律与其变形特性的研究则更为少见。本文围绕实际工况建立三维有限元数值模型,基于线性波理论计算由通航船只引发的波浪力,分析了桩基础在波浪作用下产生的水平位移,在与监测数据进行对比,验证模型建立合理的基础上,通过数值模拟方法,研究了波浪力作用下深水小尺度圆柱形群桩的内力变化、分布规律与其变形特性,并根据研究结果提出相关建议,可为实际工程和后续研究提供参考。
2 工况与监测数据
某桥梁桩基所在处水深约46 m,全桥由(5×30)m引桥和(75+4×130+75)m预应力混凝土刚构—连续梁组合体系主桥组成,结构布置简图如图1所示。基础由方形承台(10 m×10 m×4.5 m),及桩径2.5 m的圆形钻孔灌注桩组成,桩长76 m,单个承台下布置4根桩,纵桥向和横桥向桩间距均为5.9 m,如图2所示。桩身嵌入水底岩土层30m,水中自由段长46 m,承台、桩基均采用C30混凝土。水底岩土层主要包括6 m新近沉积粉质黏土、9 m砂砾卵石、4 m强风化绢云母石英片岩和15 m中风化绢云母石英片岩。
在桩基与承台施工完成时开展监测工作,波浪数据,以及由其引起的桩基水平位移采用某大型通航船只经过附近时采集的数据:波浪的波高H=0.27 m,周期T=3.50 s,波长L=19.11 m。在无行船经过、无明显引起波浪的风时,承台顶部水平位移最大仅3 mm,基本可以忽略不计。行船通过施工现场附近约10 s,在此时间内测得船行波主要引起桩基沿垂直于船行方向作小幅的周期性晃动,承台顶部最大水平位移约为15 mm。
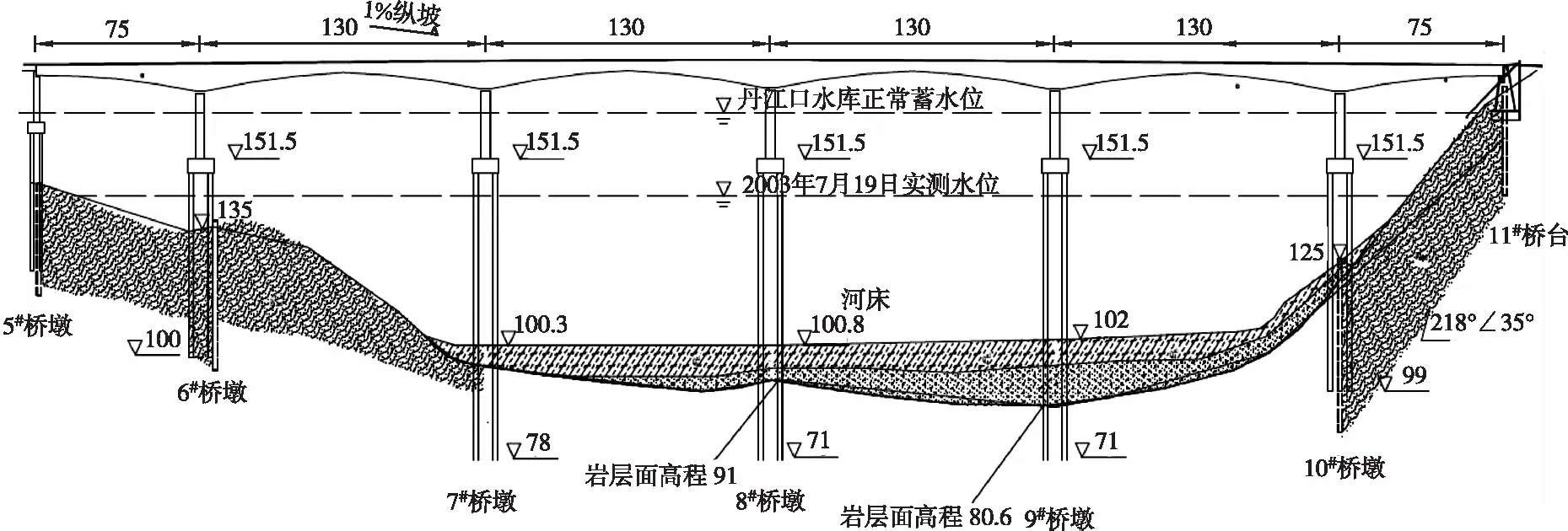
图1 桥梁布置简图Figure 1 Layout sketch of bridge

图2 承台-群桩布置简图Figure 2 Layout sketch of cap-group pile
3 数值模型的建立
3.1 承台-桩基-岩土层模型
基于实际工况和监测数据,采用Midas/GTS有限元软件建立数值模型。承台采用实体单元,桩柱采用梁单元,两者的弹性模量E为3×104MPa、泊松比υ为0.25、重度γ为24.5 kN/m3。
近沉积粉质黏土、砂砾卵石、强风化绢云母石英片岩、中风化绢云母石英片岩均采用实体单元,本构选用摩尔-库伦模型,4种岩土材料的弹性模量E、泊松比υ、重度γ、粘聚力c、内摩擦角φ如表1所示。建模时对桩与土设置接触面以模拟两者间的相互作用,同时地基边界尺寸的取值也要考虑桩土相互作用影响的范围,一般根据桩径D,水平向通常取(12~15)D,竖向取(5~10)D[12],超出此范围即认为桩的应力和变形对地基土的影响已经很小,可以忽略不计。本模型中桩径为

表1 岩土材料主要力学参数Table 1 Main mechanical parameters of geotechnical materials岩土层名称E/ MPaυγ/(kN·m-3)c/kPaφ/(°)新近沉积粉质黏土300.2716.51117砂砾卵石1500.2520.0326强风化绢云母石英片岩2×1040.2821.82528中风化绢云母石英片岩3×1040.2724.230036
2.5 m,结合各岩土层的厚度,地基模型的尺寸确定为50 m×50 m×34 m(长×宽×高),以充分考虑桩土相互作用影响的边界范围。
考虑到岩土材料的破坏通常是基于压缩、剪切变形而发生的塑性破坏,故三维模型选择以六面体网格为主生成单元,对分析的稳定性更为有利。模型中承台、桩基和新近沉积粉质黏土,采用混合网格划分方式,砂砾卵石、强风化绢云母石英片岩和中风化绢云母石英片岩采用映射网格划分方式,以最大限度地生成六面体单元为主的网格。建立的有限元模型和网格划分如图3所示。
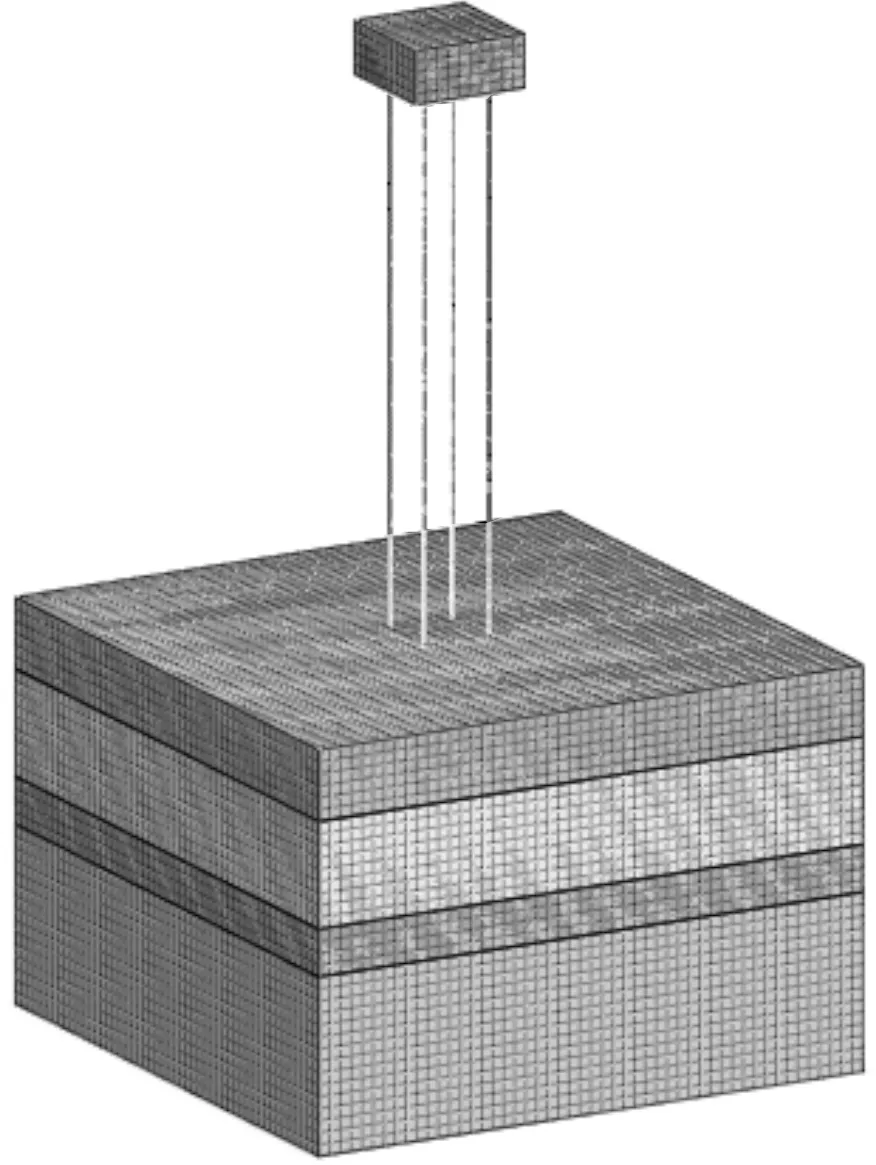
图3 有限元模型和网格划分Figure 3 Finite element model and meshing
3.2 波浪力计算原理
桩径D与波长L满足D/L=2.5/19.11=0.13<0.2,可以将其定义为小尺度桩,而水深d与波长L满足d/L=46/19.11=2.41>0.2,则可选用线性波理论描述波浪运动[13],基于线性波理论的小尺度圆柱桩波浪力计算通常采用MORISON[14]提出的公式(以下简称为用Morison方程),该公式将波浪力描述为由水质点水平速度引起的拖曳力,以及由水质点水平加速度引起的惯性力的叠加。用Morison方程求解波浪力的示意图如图4所示。

图4 波浪力求解示意图Figure 4 Schematic diagram of wave force solution
根据Morison方程,桩柱长度增量dz上的波浪力合力为:
(1)
式中:dFH为dz长度桩身所受波浪力的合力;ρ为水的密度;ux为水质点的水平速度;t为时间;CD、CM分别为拖拽力系数和惯性力系数,与桩的截面有关,按照我国现行规范[15],分别取1.2、2.0。
4 模型验证
基于Morison方程,使用MATLAB软件编制波浪力计算程序,将结果导出,并在Midas/GTS中进行动力加载,然后提交计算。由于通航船只经过施工现场附近的时间约为10 s,故此处计算了4个波浪周期,即14 s内桩基的动力响应。得到波浪力作用下桩基的最大位移云图、承台水平位移时程曲线分别如图5、图6所示。
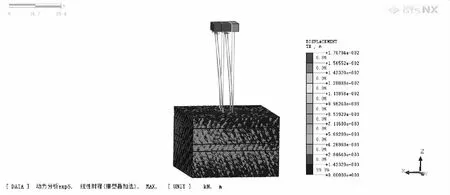
(a)顺波浪传播方向
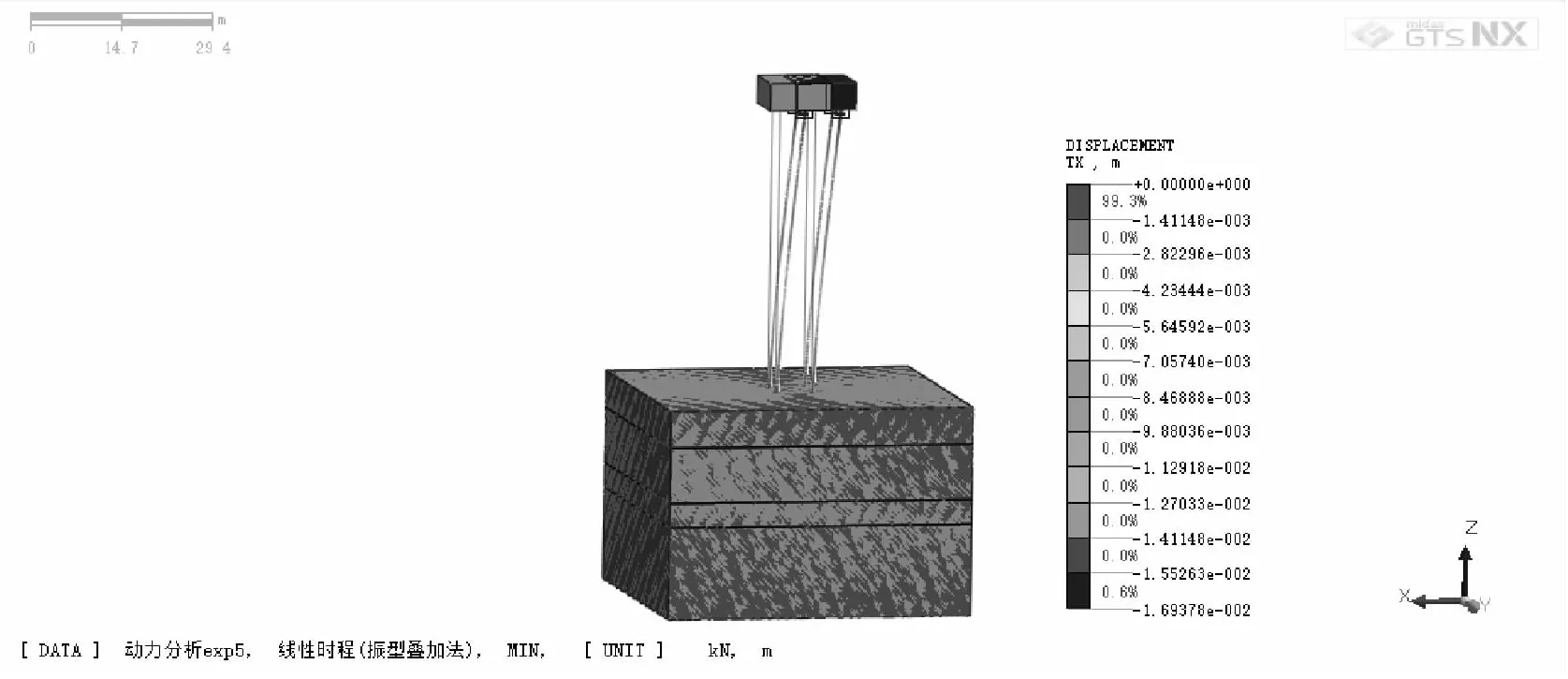
(b)逆波浪传播方向
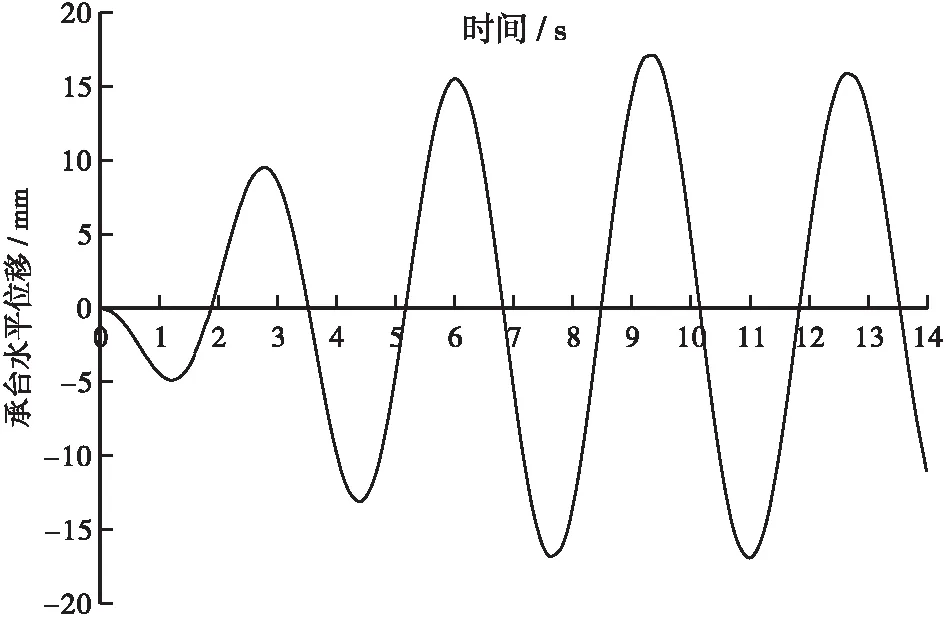
图6 承台水平位移时程曲线Figure 6 Time history curve of horizontal displacement of bearing cap
由数值模拟结果可以看出,船行波作用下承台最大水平位移约17 mm,曲线呈现出三角函数式的变化,均与实际监测结果较为接近。说明该模型基本能够反映实际工况,数值模拟结果可靠,桩身的内力与变形可基于该模型进行计算分析。
5 内力及变形的有限元分析
5.1 桩端轴力
按照波浪传播到达桩身的顺序,分别将垂直于波浪传播方向的两排桩命名为前排桩和后排桩。根据图6,选取承台水平位移时程曲线出现波谷和波峰的8个时间点:1.2、2.8、4.4、6.0、7.6、9.4、11.0、12.8 s,提取上述时间点水中自由段桩身的桩端(桩顶与桩底)轴力数据,结果显示同排桩轴力相等,各基桩的桩顶轴力与桩底轴力也相等。此处为使图表简明清晰,同一排仅选取一根桩的数据绘出。将以上8个时间点2排桩的桩端轴力数据绘制成散点图并用直线连接,如图7所示。
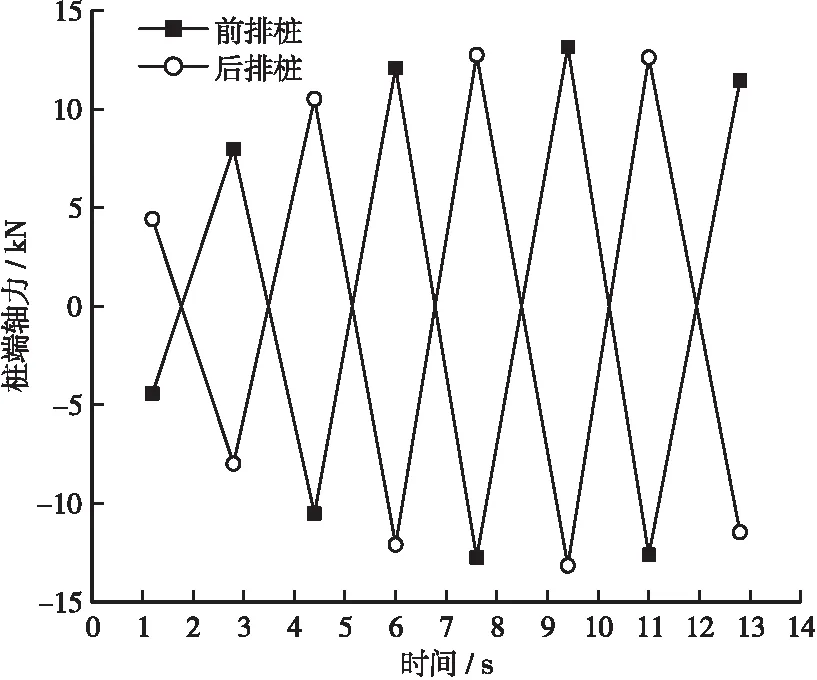
图7 桩端轴力Figure 7 Axial force of pile end
在同一时刻,前后2排桩的轴力呈现出大小基本相等,方向相反的规律,且变化速率保持一致。当受到波浪力的作用时,前排桩桩端首先出现负轴力,短时间内处于受压状态,后排桩桩端则出现正轴力,短时间内处于受拉状态,随后2排桩均出现受拉和受压状态的快速交替变换。尽管混凝土承台具有很大的重量,但桩身在水平波浪力这一周期性荷载的作用下,并非一直处于受压状态,而是表现为拉压状态的交替变换。随着波浪力作用的持续,承台达到峰值位移时,轴力也基本达到峰值。
5.2 桩端剪力
同样提取上述8个时间点水中自由段桩身的桩端剪力数据,结果显示同排桩的剪力数据也基本保持一致,而不同排桩的桩顶剪力则存在显著差异,对此,将这8个时间点2排桩的桩顶,及桩底剪力数据分别绘制成散点图并用直线连接,见图8。
可以看出,后排桩桩顶剪力通常要比前排桩桩顶剪力大,且随时间的变化速率更快,同一时刻前后排桩桩顶剪力相差最大可达25.4倍,总体峰值相差1.8倍,但绝大部分时刻剪力方向保持一致。其数值相差过大的主要原因在于承台的重量,以及前后排桩波浪的相位差。波浪首先到达前排桩,使其产生动力响应的同时,承台和后排桩同样因受到瞬时的惯性力而产生加速度,引起2排桩桩顶剪力的较大差异。而同一时刻2排桩的桩底剪力则基本
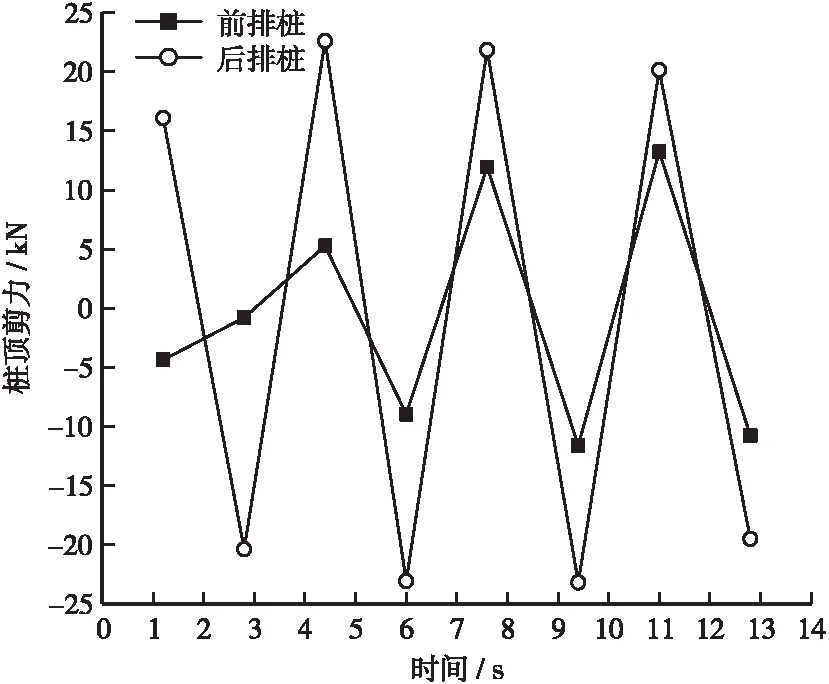
(a)桩顶剪力

(b)桩底剪力
相等且变化速率一致。由于波浪传播方向上不同排桩的桩顶剪力分配较为不均匀,因此在波浪荷载较大的工程环境中,如海洋工程等领域,需要对桩基与承台连接部位的设计和施工予以足够重视,如通过加密此处的钢筋网络、增加桩身嵌入承台的深度等措施,以防止部分连接部位出现剪切破坏。
5.3 桩身弯矩
数值模拟结果显示同排桩的弯矩也基本相同。此处,为使曲线更简洁明了,在前文所选取的8个时间点中选出4个时间点,分别为承台水平位移时程曲线出现首个波谷和波峰的1.2、2.8 s,以及出现负向和正向最大位移的7.6、9.4 s,提取上述时间点的前后排桩弯矩沿水中自由段桩身的分布,绘制曲线如图9所示。
尽管作用于不同排桩的波浪存在相位差,但由于承台的连接与岩土层的固定作用,且深水高桩具有一定柔性,在同一时刻,前后排桩的弯矩基本相等,桩身弯矩数值在水底土层部位最大,沿桩身向上逐渐减小,至桩顶位置趋于0。
5.4 桩身变形
由图5、图6可知,承台的变形最大且主要表现为水平位移,同样选取上述4个时间点,提取对应的数值模拟结果,结果显示同排桩的水平位移也保持一致。将水中自由段桩身的位移数据绘制成曲线,如图10所示。
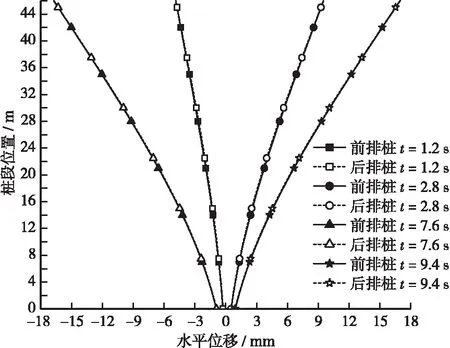
图10 桩身水平位移Figure 10 Horizontal displacement of pile body
可以看出,桩身水平位移曲线形似“倒置”的桩身弯矩曲线。同样因为承台的连接、岩土层的固定,以及深水高桩的柔性,位移的同步并不局限于桩顶与承台连接的位置,各基桩桩身相同部位的变形均基本保持一致,变形主要表现为侧弯,并沿波浪传播方向来回摆动。承台的水平位移最大,桩身嵌入土层处的位移最小,其数值接近但不等于0,说明桩身在土层中也发生了微小的位移。此前大量关于波浪力作用下深水桩基的室内模型试验与数值模拟研究中,仅考虑桩身在水中的自由段,而将桩基在水底处作固接处理,显然有一定不妥之处,桩土接触和相互作用对桩身内力和位移的影响不能忽略且有待进一步研究。
6 结论
本文主要利用有限元数值模拟,分析了水平线性波浪作用下小尺度圆柱形群桩在水中自由段桩身的桩端轴力与桩端剪力的变化规律、桩身弯矩的分布规律和桩身变形特征,主要结论如下:
a.在波浪力的作用下,垂直于波浪传播方向的同排桩桩端轴力、桩端剪力和桩身弯矩基本相等;在同一时刻,前后2排桩的桩端轴力大小相等方向相反,前排桩的桩顶剪力要小于后排桩,其同一时刻相差最大可达25.4倍,峰值相差1.8倍;前后排桩的桩底剪力与桩身弯矩基本保持相等。在水平波浪力的作用下,垂直于波浪传播方向上的不同排桩桩顶剪力分配较为不均匀,在深水桩基的设计和施工中,应对承台和桩基的连接予以足够重视,如加密连接处的钢筋网络、增大桩身嵌入承台的深度等,以避免在海洋等波浪力较大的工程环境中出现部分连接部位的剪切破坏。
b.群桩中各基桩桩身相同位置的变形基本保持一致,桩身变形主要表现为侧弯,并沿波浪传播方向作来回的周期性晃动,承台的水平位移最大,桩身嵌入土层处的位移最小但不为0,说明桩身在岩土层中也产生了一定的位移,研究中不能忽略岩土层的存在和影响。
