基于概率的连续梁桥施工变形参数敏感性分析

任 翔， 余 兴， 宋 飞， 张伊飞

(西安科技大学 建筑与土木工程学院, 陕西 西安 710054)

随着国内交通事业的发展，特别是高速铁路的大规模建设，对桥梁工程施工精度有了更高的要求。目前由于各种因素的影响，实际中出现桥梁线形与设计偏差较大情况的桥梁较多。因此，本文对桥梁施工变形影响因素进行研究，以期为桥梁设计和施工提供参考。赵晓华[1]等为研究PC梁桥结构参数对最大悬臂结构力学性能的影响，采用了对关键参数上调和下调5%～10%的方法，得到材料容重和混凝土弹性模量对主梁线形影响较大。马显红[2]、包龙生[3-4]、王今朝[5]等分别以连续梁桥和连续刚构桥梁为依托，对桥梁线形进行了敏感性分析，对关键参数上调和下调10%的方法，分别得出混凝土自重、截面抗弯惯性矩和混凝土弹性模量对桥梁线形的影响较大。ZHENG[6]等对某连续刚构桥的长期挠度进行参数敏感性分析，用对关键参数上调10%的方法，得到预应力损失对刚构桥的长期挠度影响最大。祝国华[7]等以连续梁桥为依托，以BP神经网络方法建立桥梁施工状态函数，基于蒙特卡罗算法对导致施工控制误差因素进行敏感性分析，得到锚下控制应力对施工误差影响最大的结论。姜增国[8]等研究连续刚构桥施工控制参数的敏感性，采用均匀设计法，对4个参数进行交叉线性回归，得到对于成桥线形敏感因素的预应力初始控制应力和混凝土重度。

对分析变量变化范围的选取，较少考虑基于概率分布的选取，通常对分析变量上下限进行简单的增大和减少5%或10%的处理，这样分析变量的变化范围与实际偏差较大，导致分析结果各有不同。参数敏感性分析中分析变量的选取均未考虑混凝土容重变化,以及主梁模板膨胀导致主梁截面的变化。因此，本文对预应力连续梁桥的施工变形进行敏感性分析，基于分析变量的概率分布，确定分析变量的变化范围，考虑混凝土主梁底板厚度的变化，运用龙卷风图法[9-11]，评估各分析变量对桥梁施工阶段累积变形的敏感性。

1 工程概况

某四跨预应力连续梁桥其跨径组合(45+75+75+45)m，桥梁宽度为10 m，桥梁断面采用单箱单室直腹板断面，箱梁零号块的根部梁高为4.5 m，边中跨合拢段2.5 m。梁底采用1.8次抛物线形式。主梁施工方法采用对称悬臂浇筑施工，共分9个节段。在中墩采用固定支座，其他墩采用活动支座。桥墩采用矩形墩，桩基采用群桩摩擦桩基础。连续梁总体布置图如图1所示。

图1 全桥总体布置图(单位： m)Figure 1 General layout of the bridge (Unit: m)

2 敏感性分析方法

本文选取龙卷风图法[12-13]，龙卷风图有助于比较具有较高不确定性的变量与相对稳定的变量之间的相对重要程度，强调了整体风险最大的促成因素。

本文中龙卷风图法敏感性分析如图2所示。

a.选定需要确定D的类型，如施工阶段累积变形。

b.选定随机变量X，根据其概率分布形式确定输入变量下限值XLB和上限值XUB，见图2(a)。

c.除随机变量X外别的变量选为均值，并将XLB和XUB分别输入结构模型进行分析，得D的下限值DLB和上限值DUB，见图2(a)

d.取|DUB-DLB|为D对应的“幅摆”宽度，并将其表示在初始图形中，见图 2(b)。

e.重复上述步骤直至获得所有输入变量对应的“幅摆”宽度为止， 并将其自上而下按降序重新排序。排序后的图形即为 Tornado 图，见图 2(b)。

图2 龙卷风图制作方法Figure 2 Tornado map production

3 关键参数分布特性

本文选用混凝土容重、混凝土弹性模量、混凝土梁底板厚度和预应力损失为关键参数，并对其分布特性进行研究。

3.1 混凝土容重

文献[14]进行了混凝土容重参数估计研究，共取得数据为36组，对其分布形式进行了探究，发现其分布符合正态分布，且给出了具体的正态分布回归方程，取其均值为26.2 kN/m3，标准差为0.262 kN/ m3，将该结果作为本文分析基本参数。故以概率为95%的C50混凝土容重置信区间为(25.686 kN/ m3，26.714 kN/ m3)。

3.2 混凝土弹性模量

混凝土弹性模量的变化与混凝土的龄期、养护条件、配合比、温湿度等有关，文献[15]中就在标准情况下的28 d养护期的混凝土弹性模量与规范给定的值进行对比，实际得出的C50混凝土弹性模量最大超出规范值的20%，文献[16]中采用的混凝土弹性模量的分布形式属于正态分布，并给出了拟合正太分布公式，其均值为E，标准差0.06E，故本文选取以置信度为95%的混凝土弹性模量作为控制变量，其均值采用1.1E，确定C50混凝土弹性模量的置信区间为(3.48752×104MPa，4.32248×104MPa)。弹性模量最大值与文献[8]所得数据相符。

3.3 主梁底板厚度差值

混凝土主梁在浇筑过程中，混凝土主梁模板易发生胀模，尤其是底板位置较为严重，导致主梁底板的实际厚度会与设计值有一定的偏差。通过对于较多工程实际施工中的底板厚度的测量数据统计，得出混凝土梁底板实际浇筑厚度与设计厚度值的偏差为10 mm附近，由于已有数据的总量较少，无法得出具有较为普遍性的表达式，根据工程经验，假定其分布为正态分布，其均值为10 mm，令其以置信度为95%时的底板厚度误差值置信区间为(0 mm，+20 mm)。

3.4 预应力损失

在实际施工中，主梁有效预应力对于主梁施工阶段累积变形具有较大的影响，因此研究预应力损失对施工中的影响很有必要。文献[17]对预应力损失进行了500000次抽样，得到预应力损失的拟合正态分布函数公式。并且其预应力损失均值占张拉控制应力均值的22.2%，这表明其取值是较为合理的，符合工程设计规范中的20%对预应力损失的估计。其均值309.80 MPa，标准差为33.09 MPa，R2=0.986，以置信度为95%估计预应力损失值的置信区间为(244.94 MPa，374.65 MPa)。置信区间长度为129.71 MPa，占均值的0.4。

敏感性分析所选取的控制变量以及参数，控制变量分布特征汇总如表1所示。

表1 关键参数分布形式和取值范围Table 1 Distribution form and value range of key parameters类别分布类型均值置信度置信区间混凝土容重γ/(kN·m-3)正态分布[9]26.295%(25.686,26.714)混凝土弹性模量E/MPa正态分布[11]3.905×10495%(3.487 52×104,4.322 48×104)底板厚度偏差d/mm正态分布1095%(0,20)预应力损失σL/MPa正态分布[14]309.8095%(244.94,374.65)

4 有限元模型与分析工况

采用有限元软件Midas Civil建立某四跨预应力连续梁模型，采用梁单元，梁单元的截段划分根据设计悬臂浇筑长度进行划分，每块节段浇筑细分为挂篮到位、混凝土浇筑、混凝土达到强度、预应力张拉、全桥共建施工阶段为55个，考虑混凝土材料的收缩徐变。中墩位置支座为固定支座，采用固定约束，释放y轴的转动约束，其他墩位置支座为活动支座，释放x轴方向位移和y轴方向的转动约束，有限元模型如图3所示。

图3 有限元模型Figure 3 Finite element model

5 分析结果

对各控制变量敏感性分析结果进行提取，分析不同分析变量对连续梁施工阶段累积变形的影响。工况1为基准模型，各分析变量取均值，其他工况表示选取不同分析变量的上下限，分析变量表如表2所示。由于桥梁为对称桥梁，选左半幅桥施工阶段累积变形进行分析。

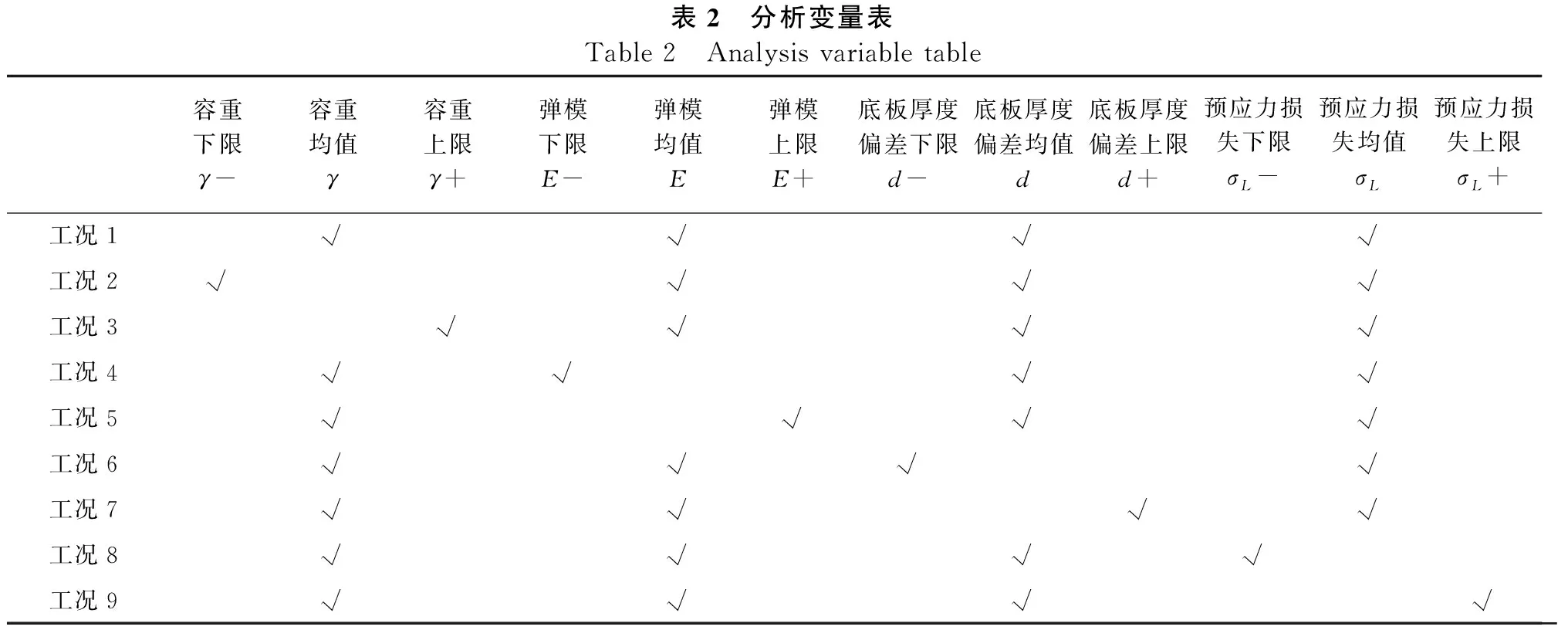
表2 分析变量表Table 2 Analysis variable table容重下限γ-容重均值γ容重上限γ+弹模下限E-弹模均值E弹模上限E+底板厚度偏差下限d-底板厚度偏差均值d底板厚度偏差上限d+预应力损失下限σL-预应力损失均值σL 预应力损失上限σL+工况1√√√√工况2√√√√工况3√√√√工况4√√√√工况5√√√√工况6√√√√工况7√√√√工况8√√√√工况9√√√√

5.1 混凝土容重的影响

由图4可知，在2号墩右侧3/4最大悬臂处和3号墩左侧3/4最大悬臂处的施工阶段累积变形差别明显，在2号墩右侧3/4最大悬臂处处，取容重置信下限时，施工阶段累积变形增加1.18 mm，增大了3.13%；取容重置信上限，其施工阶段累积变形降低，降低1.21 mm ，减少3.31%。在3号墩左侧3/4最大悬臂处，容重置信下限时，其施工阶段累积变形增大1.19 mm，升高了5.66%;容重为置信上限时，其施工阶段累积变形减少1.21 mm，降低了6.24%。

5.2 弹性模量的影响

由图5可知，2号墩右侧3/4最大悬臂处和3号墩左侧3/4最大悬臂处的差值最大，当取弹性模量置信下限时，其施工阶段累积变形分别减少2.37、1.31 mm，分别降低了6.30%、6.33%。当取弹性模量置信上限时，其施工阶段累积变形分别增大1.92、1.05 mm，分别升高了4.80%、4.78%。

图4 容重对施工阶段累积变形影响Figure 4 Influence of bulk density on cumulative deformation during construction 注：f为基准模型施工阶段累积变形；fγ-为容重下限施工阶段累计变形；fγ+为容重上限施工阶段累积变形；Δfγ-为容重下限与基准的差值；Δfγ+为容重上限与基准的差值 。

注： f为基准模型施工阶段累积变形；fE-为弹性模量下限施工阶段累积变形;fE+为弹性模量上限施工阶段累积变形；ΔfE-为弹性模量下限与基准的差值；ΔfE+为弹性模量上限与基准的差值图5 弹性模量对施工阶段累积变形影响Figure 5 Effect of elastic modulus on cumulative deformation during construction

5.3 底板厚度差值的影响

由图6可知，2号墩右侧3/4最大悬臂处和3号墩左侧3/4最大悬臂处施工阶段累积变形差值最大，在2号墩右侧3/4最大悬臂处，当底板厚度差值分别取置信上下限时，其施工阶段累积变形分别降低了0.05、0.11 mm，分别降低了0.14%、0.3%。在3号墩左侧3/4最大悬臂处，底板厚度差值取置信下限时，增大了0.14 mm，升高了0.67% ，底板厚度差值取置信上限时，减少了0.32 mm，降低了1.55% 。

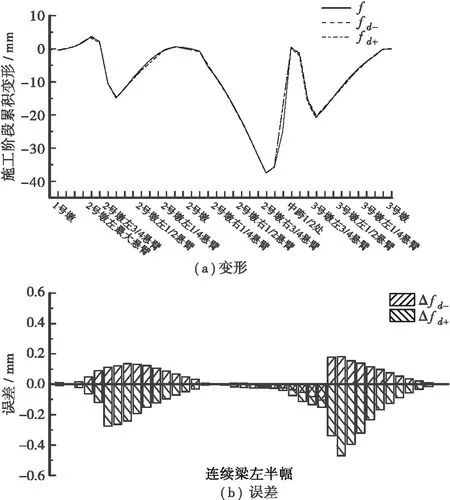
注： f为基准模型施工阶段累积变形；fd-为底板厚度差值下限施工阶段累积变形；fd+为底板厚度差值上限施工阶段累积变形;Δfd-为底板厚度差值下限与基准的差值；Δfd+为底板厚度差值上限与基准的差值图6 底板厚度对施工阶段累积变形影响Figure 6 The influence of the thickness of the bottom plate on the cumulative deformation during the construction phase

5.4 预应力损失的影响

如图7所示，施工阶段累积变形差值最大为2号墩右侧3/4最大悬臂处和3号墩左侧3/4最大悬臂处。当取预应力损失置信下限时，其施工阶段累积变形分别增大3.34、4.33 mm，分别升高了8.59%、19.81%。当取预应力损失置信上限时，其施工阶段累积变形分别减少3.46、4.44 mm，分别降低了10.09%、27.21%。

注： f为基准模型施工阶段累积变形；fσL-为预应力损失下限施工阶段累积变形;fσL+为预应力损失上限施工阶段累积变形;ΔfσL-为预应力损失下限与基准的差值；ΔfσL+为预应力损失上限与基准的差值图7 预应力损失对施工阶段累积变形影响Figure 7 Effect of prestress loss on cumulative deformation during construction

将各单参数模型与基准模型结果进行对比，选取的2号墩右侧3/4最大悬臂截面施工阶段累积变形进行对比，如图8所示，运用龙卷风图法将各参数对于施工阶段累积变形的敏感性进行排序，得出其敏感性程度。其对施工阶段累积变形影响程度依次为预应力损失、混凝土弹性模量、混凝土容重，及主梁底板厚度偏差。

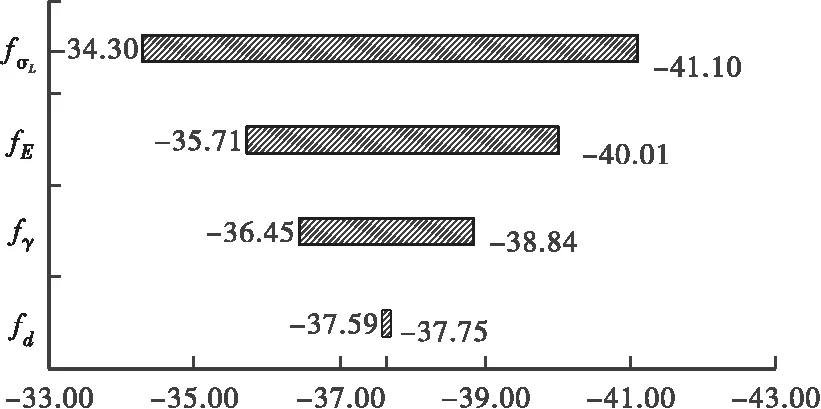
注： fσL为预应力损失施工阶段累积变形；fE为混凝土弹性模量施工阶段累积变形；fγ为混凝土容重施工阶段累积变形;fd为主梁底板厚度差值施工阶段累积变形图8 龙卷风图(单位： mm)Figure 8 Tornado graph (Unit: mm)

5.5 讨论

本文基于概率的方法对分析变量的变化范围进行取值，采用龙卷风图法进行分析，所得到结果为预应力损失对主梁线型的影响最大，其次为混凝土弹性模量。文献[1-7]对桥梁参数敏感性分析的控制变量的选取均没有考虑控制变量的函数分布，由此，导致其敏感性分析中所得到的敏感性关键参量与本文相差较大。文献[1-6]表明对主梁线型影响较大的关键变量包括混凝土弹性模量、混凝土容重和截面抗弯惯性矩，文献[7]得到锚下控制应力对施工误差影响最为显著，文献[8]表明预应力初始控制应力和混凝土重度对成桥线形影响最大，文献[6-8]与本文结果中的预应力损失为敏感性关键参量相符合。

6 结论

本文通过对连续梁桥进行敏感性分析，探究各分析变量对桥梁施工阶段累积变形的影响，采用龙卷风图进行敏感性分析，得到以下结论：

a.对施工阶段累积变形的重要性依次为预应力损失、混凝土弹性模量、混凝土容重、主梁底板厚度偏差。其中预应力损失、弹性模量对施工阶段累积变形的影响均大于5%，预应力损失最大影响大于10%。

b.底板厚度误差对施工阶段累积变形的影响可以忽略。

c.挂篮变形、施工临时荷载堆载、混凝土徐变等分析变量的函数分布探究较少，因此可供选取的分析变量数量较少，可能会导致关键参数选取不足，并且混凝土性能受地域性影响较大，应对不同地域的分析变量函数分布进行探究。