强冲击荷载下RC板失效仿真研究

2022-06-07刘慧萍银昱杰

建筑科学与工程学报 2022年3期

梁婧，刘慧萍，黄华，银昱杰

(1. 西安工业大学建筑工程学院，陕西西安 710021； 2. 长安大学建筑工程学院，陕西西安 710061))

0 引言

近年来，由于恐怖袭击、局部战争等，混凝土结构常常遭受爆炸等袭击，LS-DYNA软件常用来处理此类问题的非线性分析[1-2]。在进行炮弹侵彻[3-5]贯穿混凝土材料仿真分析时，常用JOHNSON_HOLMQUIST_CONCRETE(HJC)模型来描述混凝土材料，并添加失效准则控制材料失效。LS-DYNA关键字用户手册[6]中HJC模型包含一个失效控制参数FS值。文献[7]从理论层面对FS值进行了分析，通过对Hanchak等[8]的试验数值模拟得出FS值大于等于0.67，进而定量分析得到FS值的假设值为1.34。文献[9]对FS值给出了更简单直白的解释，量化计算出FS值为1.3。文献[10]采用DOE分析参数灵敏度，在0.3～0.7之间调试FS值。ADD_EROSION为HJC模型提供了考虑单一因素或多种因素共同控制材料失效的方法。文献[11]、[12]采用单一失效准则控制材料失效，文献[13]、[14]采用最大静水压力和最大剪应变失效准则，文献[15]主要研究了主应变、剪应变、应力失效准则参数以及它们之间相互耦合作用对侵彻能力的影响。LS-DYNA软件提供了控制失效的多种方式，但如何更为合理地进行混凝土材料失效控制，目前还没有定论。

本文基于LS-DYNA，构建单个弹体垂直冲击RC板的有限元模型，采用HJC模型和失效准则描述混凝土材料，通过对比分析弹体残余速度的计算结果和试验结果，得到FS值、主应变、剪应变和应力等参数对侵彻贯穿效应的影响规律，为HJC材料模型在强冲击荷载问题中的应用提供参考。

1 LS-DYNA建模

本文以Hanchak等[8]对混凝土强度为48 MPa的RC板的侵彻试验为对照，数值模拟直径为25.4 mm、长径比为5.657的实心弹体侵彻贯穿尺寸为610 mm×510 mm×178 mm、强度为48 MP的布有3层钢筋的混凝土板，研究参数FS值对侵彻贯穿效应的影响，有限元模型[16-19]如图1所示，钢筋网及弹体位置如图2所示。试验中钢筋网间距为76 mm，大于弹体直径，弹体击中钢筋的概率较低，本文主要模拟弹体穿过RC板钢筋网眼的工况。

图1 有限元模型Fig.1 Finite Element Model

图2 钢筋平面布置及弹体冲击位置(单位:mm)Fig.2 Rebar Layout and Impact Position of Projectile (Unit:mm)

2 HJC模型

2.1 HJC本构

HJC[20-22]本构模型可用于描述大应变、高应变率和高压力下的混凝土材料，其屈服应力表达式为

(1)

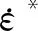
2.2 失效类型

FS值可表示失效类型，FS值小于0表示模拟计算中选择了用损伤因子D控制材料模型失效；FS值等于0表示模拟计算中选择了拉伸破坏控制材料模型失效；FS值大于0表示模拟计算中选择了受压破坏控制材料的失效[7,9]。本文在0～1.5之间调整FS值，计算得到的残余速度如表1所示，计算值与试验值的对比如图3所示。

表1 不同FS值的残余速度Table 1 Residual Velocity of Different FS Values

图3 不同FS值时的残余速度计算值和试验值对比Fig.3 Comparison Between Residual Velocity Calculated Value and Test Value of Different FS Values

根据Hanchak等[8]的试验，弹体极限贯穿速度在301～360 m·s-1之间。从表1可以看出，当FS值取0或1.0～1.5时，部分模型的弹体未能贯穿RC板，与试验现象不符。当FS值为0.1～0.9时，残余速度计算值随FS值增大而减小。当FS值为0.3～0.5时，弹体以606、746、1 059 m·s-1的速度侵彻贯穿RC板时计算值与试验值的吻合程度较好。当FS值为0.7～0.8时，弹体以360、434 m·s-1的速度侵彻贯穿RC板时计算值与试验值吻合程度较好。

从图3可以看出，当FS值为0.1～0.5时，残余速度计算值高于试验值，计算值曲线可近似看成是相互平行的，在速度一定的条件下，计算结果呈现出等差递减的趋势，但FS值为0.3～0.5时的计算值曲线与试验值曲线吻合较好。当FS值为0.6～0.9时，计算值低于试验值，初始冲击速度为606、746、1 058 m·s-1的计算结果误差较大，初始冲击速度为360、434 m·s-1的计算结果吻合较好。当FS值为0或1.0～1.5时，模拟计算结果与试验值误差很大且部分计算结果不合理，FS值取值越大，这种不合理结果出现越多。总体上，FS值为0.3～0.8时，残余速度计算值曲线与试验值曲线吻合良好。

结合表1和图3可知：当FS值为0.5时得到的残余速度曲线吻合较好，但两端吻合较差；FS值为0.8的计算结果两端吻合良好。本文尝试在FS值为0.8的条件下研究失效参数对弹体冲击RC板侵彻贯穿效应的影响。

3 失效准则对侵彻贯穿能力的影响

3.1 ADD_EROSION模型

LS-DYNA中的许多本构模型不允许失效和侵蚀。ADD_EROSION模型提供了一种在这些模型中包含失效的方法。关于混凝土材料失效准则的研究主要集中于主应变、剪应变、应力失效准则参数以及它们之间相互耦合作用对侵彻能力的影响。对应到最新失效模型[23]中，即控制最小破坏压力(MNPRES)、最大破坏主应变(MXEPS)和最大破坏剪应变(EPSSH)来研究混凝土材料的失效。

3.2 MXEPS值对侵彻贯穿效应的影响

在FS值为0.8的情况下，MXEPS值取0.2～0.3，每隔0.025递增，计算结果如图4所示。

图4 不同MXEPS值的残余速度曲线(FS值为0.8)Fig.4 Residual Velocity Curves of Different MXEPS Values (FS Value Is 0.8)

给混凝土材料添加主应变失效准则得到的计算结果明显优于仅通过HJC模型参数FS值为0.8时控制材料失效的结果，与试验值曲线更为吻合。残余速度计算值随着MXEPS值增大而减小，初始速度为434、606、746 m·s-1的计算值下降幅度不大；初始速度为360 m·s-1的计算值降幅相对较大，降低了65 m·s-1；初始速度为1 058 m·s-1的计算相对误差从-2%增加到-10%。MXEPS值为0.25时残余速度的计算值曲线与试验值曲线吻合程度更好。

设置MXEPS值为0.3，取FS值为0.5、0.8、1.3分别进行模拟，计算结果如图5所示。MXEPS取值一定，3条残余速度曲线仅有微小的差别。FS值为0.8的曲线和FS值为1.3的曲线近乎重合。通过比较初始速度为360 m·s-1和1 058 m·s-1的计算结果，发现FS值为0.8的曲线拟合优于FS值为0.5的曲线。

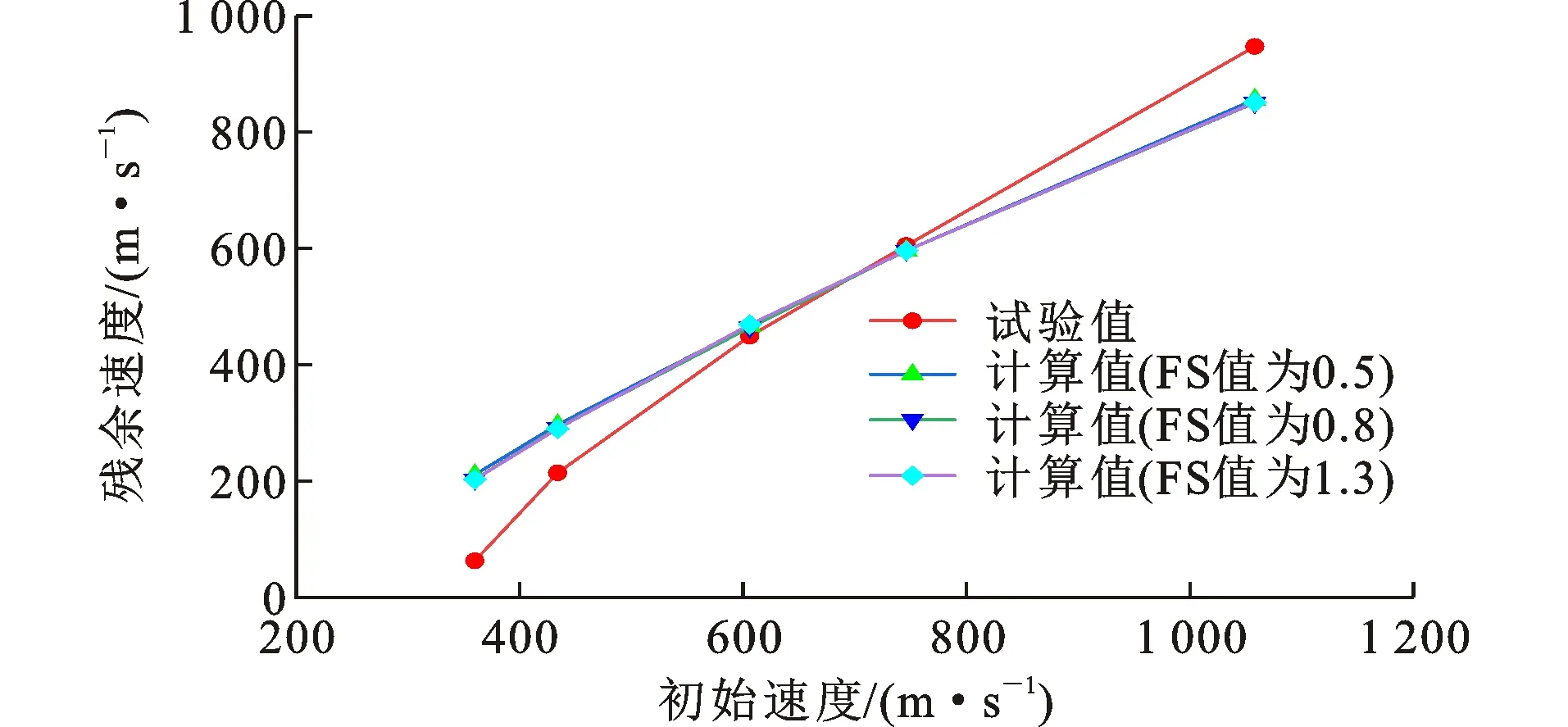
图5 不同FS值的残余速度曲线(MXEPS值为0.3)Fig.5 Residual Velocity Curves of Different FS Values (MXEPS Value Is 0.3)

3.3 EPSSH值对侵彻贯穿效应的影响

在FS值为0.8的情况下，EPSSH值取0.35～0.55，每隔0.05递增，计算结果如图6所示。

图6 不同EPSSH值的残余速度曲线(FS值为0.8)Fig.6 Residual Velocity Curves of Different EPSSH Values (FS Value Is 0.8)

添加剪应变失效准则得到的计算结果优于仅通过HJC模型参数FS值为0.8时控制材料失效的计算结果，与试验值更为吻合。残余速度计算值随EPSSH值的增大而减小，初始速度为434、606、746 m·s-1的计算值下降幅度不大；初始速度为360 m·s-1的计算值下降幅度相对较大，降低了54 m·s-1，初始速度为1 058 m·s-1的计算相对误差从-2%增到-11%。EPSSH值为0.45时残余速度的计算结果曲线与试验值曲线吻合程度更好。

EPSSH值为0.45时，取FS值为0.5、0.8、1.3分别进行模拟计算，结果如图7所示。EPSSH取值一定时，3条残余速度曲线仅有微小的差别。FS值为0.8的曲线和FS值为1.3的曲线近乎重合。通过比较曲线两端，发现FS值为0.8的曲线与试验曲线吻合更好。

图7 不同FS值的残余速度曲线(EPSSH值为0.45)Fig.7 Residual Velocity Curves of Different FS Values (EPSSH Value Is 0.45)

3.4 MNPRES值对侵彻贯穿效应的影响

根据Hanchak等[8]的研究，强度为48 MP的混凝土材料最小破坏压应力为-4 MPa。在MNPRES等于-4 MPa的条件下，调整参数FS值研究弹体冲击RC板侵彻贯穿效应，计算结果如表2所示。MNPRES值不变时，参数FS值的大小不影响计算结果。考虑拉伸失效计算得到的残余速度近乎等于初始冲击速度，即模拟中用该失效准则描述的混凝土材料破坏太早，这与试验现象不符，说明仅采用拉伸失效准则描述混凝土材料并不合适。

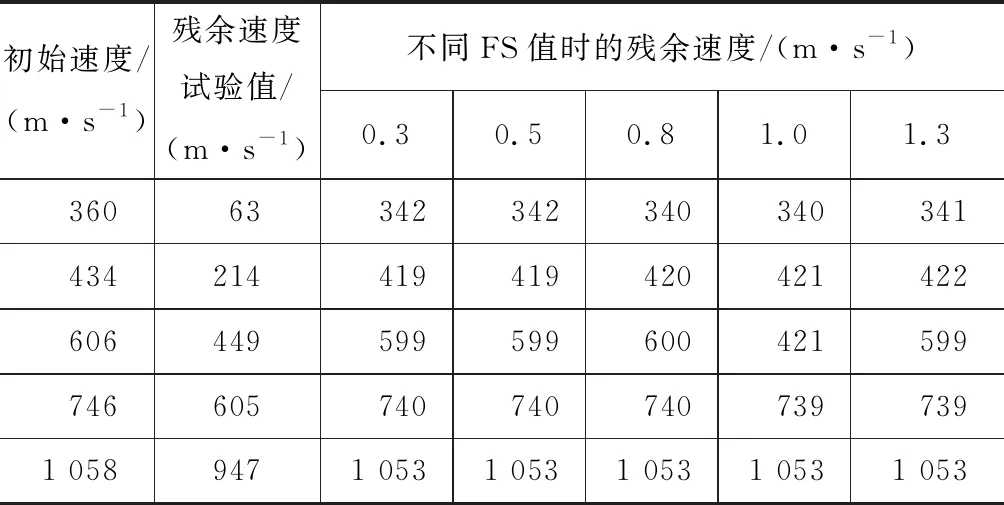
表2 不同FS值的残余速度(MNRES值为-4 MPa)Table 2 Residual Velocity of Different FS Values (MNRES Value Is -4 MPa)

3.5 MXEPS和EPSSH共同作用

在FS值为0.8的条件下，考虑主应变失效准则和剪应变失效准则共同作用，研究弹体冲击RC板侵彻贯穿效应的影响。MXEPS值取0.225、0.250和0.275，EPSSH值取0.4、0.45和0.5时，计算结果如图8所示。

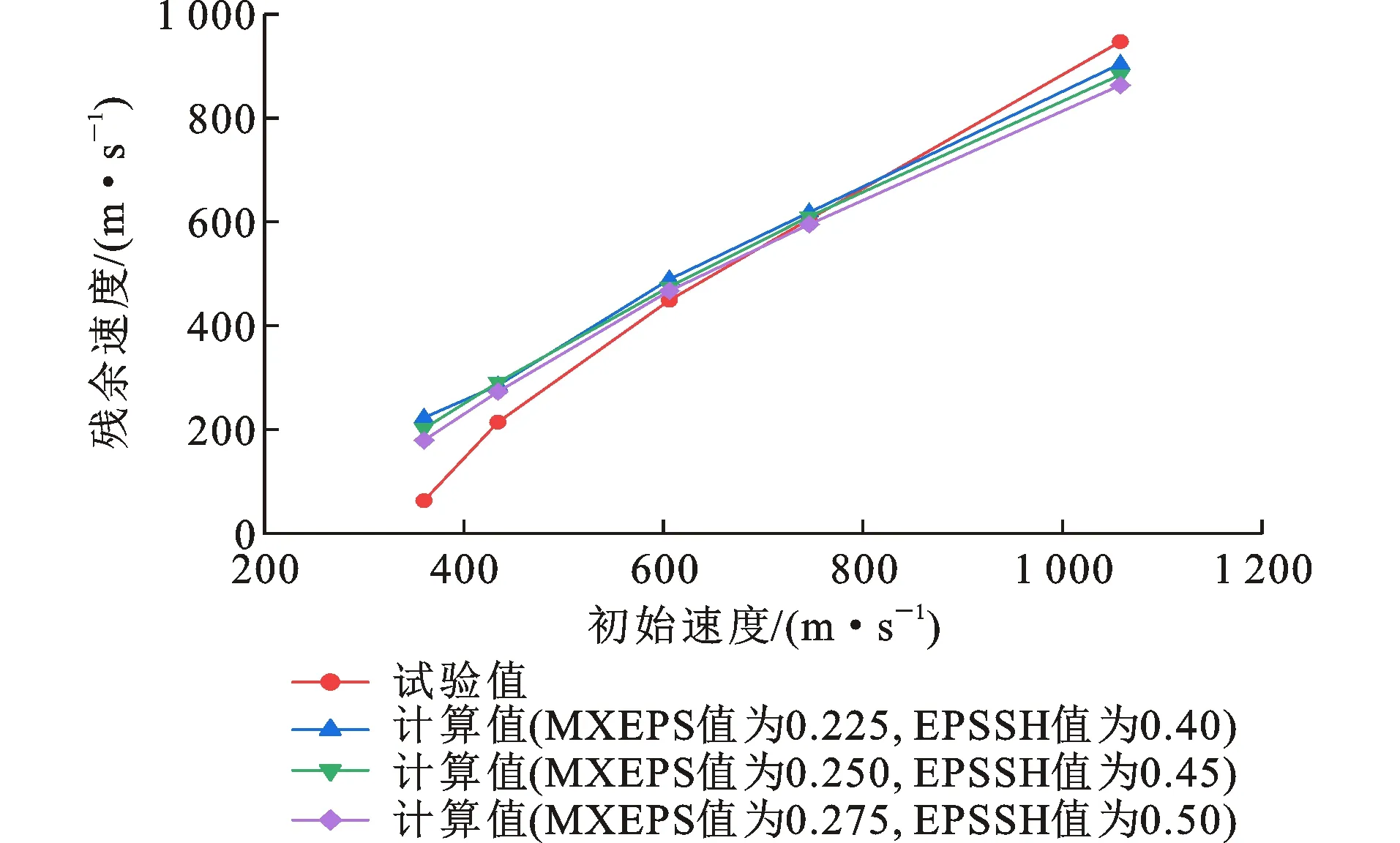
图8 MXEPS和EPSSH共同作用下的残余速度曲线(FS值为0.8)Fig.8 Residual Velocity Curves Under Combined Action of MXEPS and EPSSH (FS Value Is 0.8)

从图8可以看出，MXEPS和EPSSH的取值越大，残余速度计算结果越小。总体上看FS值为0.8、MXEPS值为0.25、EPSSH值为0.45的计算值曲线与试验值曲线吻合更好。当设置参数MXEPS值为0.25、EPSSH值为0.45时，取FS值为0.5、0.8、1.3分别进行模拟计算，结果如图9所示，FS值为0.8的计算值曲线拟合优于FS值为0.5的计算值曲线。

图9 不同FS值的残余速度曲线(MXEPS值为0.25,EPSSH值为0.45)Fig.9 Residual Velocity Curves of Different FS Values (MXEPS Value Is 0.25,EPSSH Value Is 0.45)

3.6 考虑包含MNPRES的多参数共同作用

MNPRES值为-4 MPa时，考虑主应变失效、剪应变失效作用，研究弹体冲击RC板侵彻贯穿效应，计算结果如表3所示。

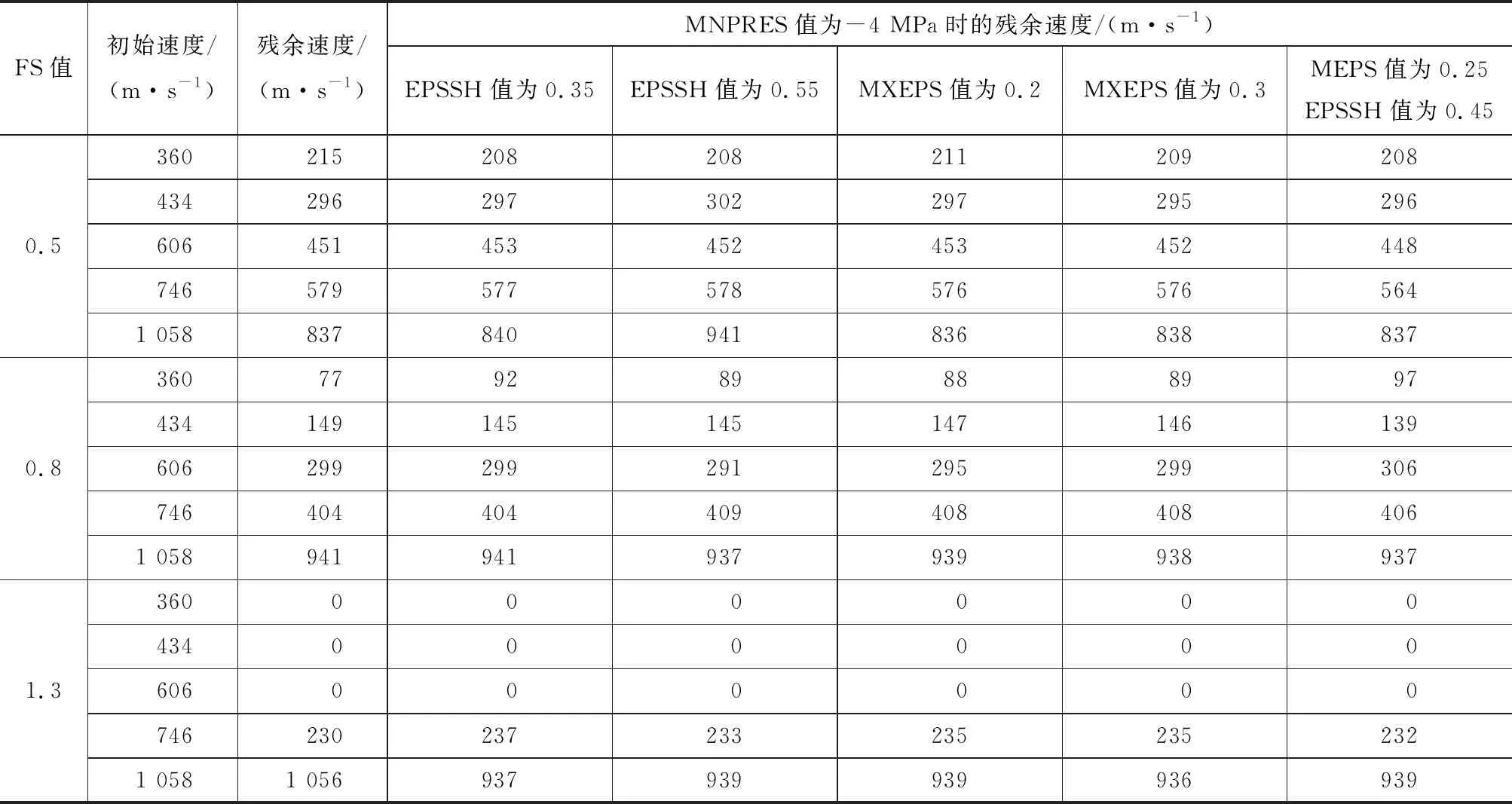
表3 多个参数共同作用下模拟得到的残余速度Table 3 Residual Velocity Simulated by Combined Action of Multiple Factors

考虑拉应力失效和剪应变失效、拉应力失效和主应变失效与拉应力失效、主应变失效、剪应变失效这3种情况下计算得到的残余速度几乎相同，且与仅考虑参数FS值作用的计算结果保持一致。该计算结果与试验值相差很多，但比仅考虑MNPRES作用的计算结果要好。在弹体侵彻贯穿较薄RC板的模拟计算中考虑拉伸失效作用并不合适。这也反映了在强冲击荷载作用下，混凝土材料拉伸断裂占比很小，HJC模型不能很好地反映出材料的动态拉伸失效现象。