部分约束下组合梁柱子结构抗连续倒塌机理

钟炜辉，段仕超，高 迪，谭 政

(1. 西安建筑科技大学 土木工程学院，陕西 西安 710055；2. 西安建筑科技大学 结构工程与抗震教育部重点实验室，陕西 西安 710055)

0 引 言

建筑结构的连续性倒塌是结构在经过初始的局部破坏后，扩展到与破坏构件相连的其他构件，最终造成了与初始破坏不成比例的破坏[1]。这种破坏对人们的生命财产有着巨大的威胁。因此，结构抗连续性倒塌性能研究成为土木工程行业的研究热点。

近年来，国内外众多学者对结构的抗连续倒塌性能进行了一系列研究[2-5]。梁柱子结构具有受力明确、结构形式简单、便于试验等优点，是目前最为常见的研究对象，当前研究主要集中在节点类型[6-8]、高跨比[9-10]、压型钢板[11]、楼板组合作用[12-13]、动态响应[14-15]等对子结构抗倒塌性能的影响。由于建筑结构中发生倒塌破坏的构件具有不确定性，在实际情况中，失效柱的位置是随机的，而不同的边界约束(失效柱位置)会影响结构的抗力机制。因此，探究不同边界约束的子结构抗倒塌性能是十分必要的。黄华等[16]认为柱失效位置和柱距是影响钢筋混凝土(RC)框架结构连续倒塌能力最重要的参数。Lew等[17]基于钢筋混凝土梁柱子结构，重点探究侧向约束对子结构抗倒塌能力的影响。Yu等[18]基于试验和理论分析方法讨论了边界条件对钢筋混凝土梁柱子结构的抗倒塌性能影响。Kang[19]通过试验研究了钢筋混凝土梁柱子结构在倒塌过程中的破坏模式，对比分析了各机制的抗力发展情况。上述研究对象大多是混凝土梁柱子结构，而对于组合梁柱子结构的边界条件研究较少。此外，由于试验成本较大，无法对所有关键参数进行试验研究，当前研究人员主要通过数值模拟的方式对相关参数进行分析[20-22]。

基于上述情况，课题组进行了不同边界条件下组合梁柱子结构的抗连续倒塌试验[23]。当结构的次边柱发生破坏时，两跨三柱的子结构一侧有梁端约束，另一侧无梁端拉结，称为部分约束子结构。次边柱失效的部分约束组合梁柱子结构(WUFG-S)的抗倒塌性能影响因素众多，本文以WUFG-S试件为研究对象，利用ABAQUS有限元软件分析边界约束侧向刚度、边柱尺寸、边柱轴压比等参数对组合梁柱子结构抗连续倒塌性能的影响。

1 数值模型建立

1.1 模型概述

图1 部分边界约束的组合梁柱子结构模型(单位:mm)Fig.1 Model of Composite Beam-column Substructure with Partial Boundary Constraints (Unit:mm)

根据钢结构设计标准[24]设计了一个尺寸为4 500 mm×7 500 mm×3 300 mm的6层钢框架组合结构。在结构的倒塌分析中，直接影响区域被认为是在失效柱的上方楼层和与失效柱相连的两跨区域，此区域是结构连续倒塌分析和设计的重点；其他区域称为间接影响区域，此区域主要为直接影响区域提供侧向约束[25]。本文的主要研究对象是直接影响区域，为便于分析可将其简化为图1所示的两跨三柱型子结构，其中L为组合梁的跨长，Lc为边柱长度。边柱上下层的反弯点近似位于层高中部，有梁端约束侧伸出边柱L/4长度以模拟间接影响区域的水平拉结作用[26]。

本文所建立的足尺模型梁柱截面尺寸分别为HM450×300×11×18、HW400×400×13×21，梁跨长4 500 mm，边柱长3 300 mm。钢材型号为Q235B，混凝土强度等级为C25，楼板有效宽度为1 500 mm，厚度为100 mm，保护层厚度为20 mm。

钢筋型号为HPB300，纵向受力钢筋采用φ14@150，水平分布钢筋为φ10@200，钢筋网双层双向布置。钢梁和楼板间通过双排布置的直径为19 mm的栓钉连接，排距为150 mm，间距为210 mm。梁柱节点采用加梯形盖板栓焊连接节点(CPS)，剪切板尺寸为340 mm×110 mm×14 mm，上下盖板厚10 mm。螺栓采用10.9级M22高强摩擦型螺栓。相关节点细部构造及构件详细尺寸如图2所示。

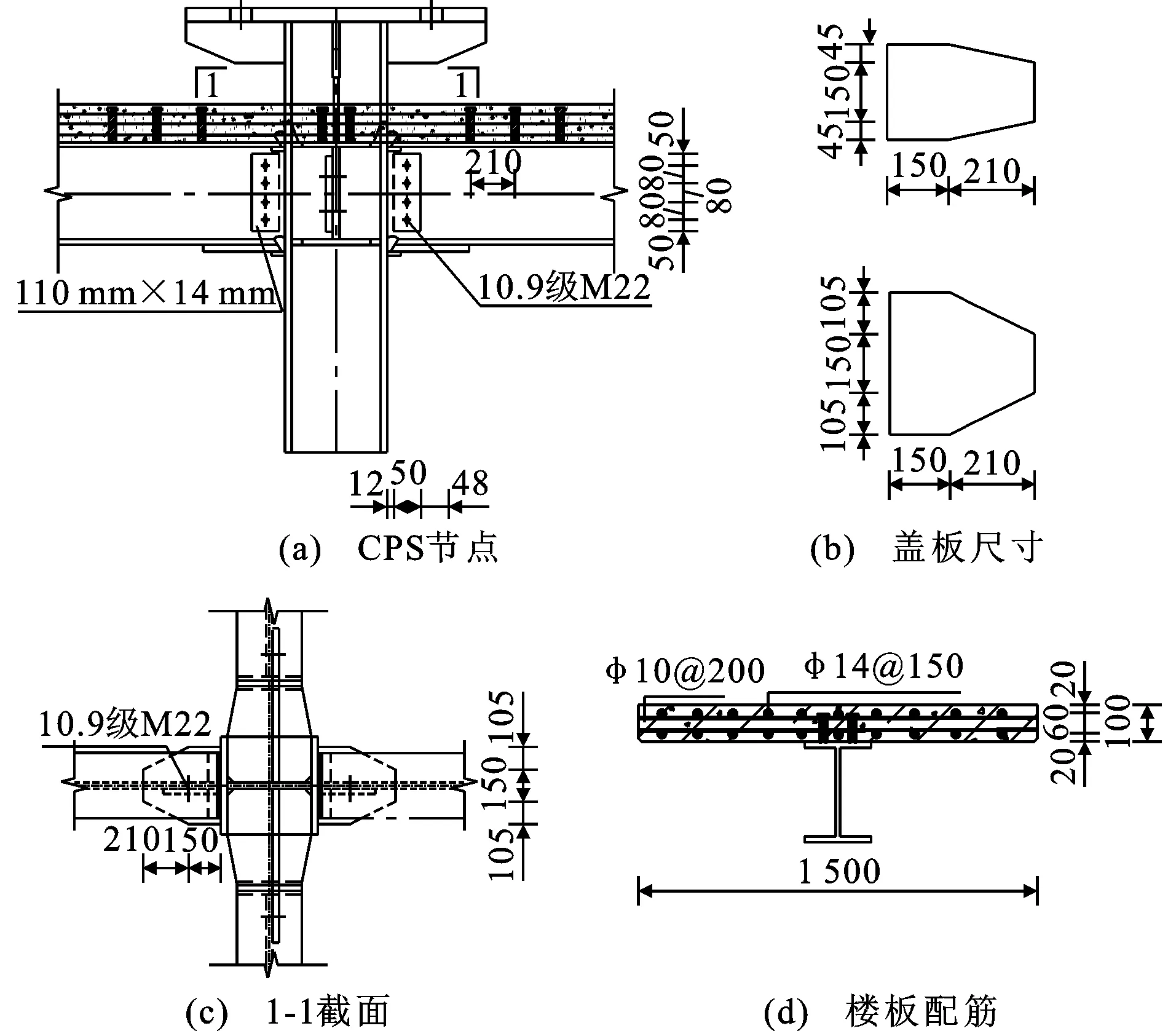
图2 节点构造及楼板配筋(单位:mm)Fig.2 Connection Structure and Slab Reinforcement (Unit:mm)

1.2 材料本构关系

通过ABAQUS软件进行有限元建模，钢筋采用双折线强化本构；钢材屈服强度为235 MPa，极限抗拉强度为370 MPa，采用二次流塑四阶段模型本构[26]。钢材的断裂采用延性金属失效准则，参考文献[27]、[28]，确定断裂应变、三轴应力、应变率等参数，使钢材达到对应的断裂应变值时发生断裂；螺栓采用10.9级M22高强摩擦型螺栓，螺栓预紧力为190 kN，屈服强度为900 MPa，极限抗拉强度为1 000 MPa；混凝土材料采用《混凝土结构设计规范》(GB 50010—2010)附录C[29]中的混凝土单轴受拉及受压本构关系，利用塑性损伤模型模拟混凝土的受力性能。

1.3 边界条件、单元类型与网格划分定义

通过在中柱柱顶施加竖向位移模拟中柱失效过程，采用平滑分析步幅值，约束平面外侧移和扭转。两边柱顶端施加轴压比为0.3的竖向荷载，模拟上部结构对边柱的荷载作用，边柱底部设置为铰接。右侧梁端通过建立轴向连接单元与固定板件连接以模拟周边约束的拉结作用，轴向连接单元另一侧设为固定边界，周边构件为子结构提供的侧向刚度(简化为轴向弹簧刚度)K输入值可通过组合梁为子结构提供的侧向刚度Kab与边柱为子结构提供的侧向刚度Kac按式(1)～(4)计算[30]。

(1)

Kab=Kb+Kp+Kr

(2)

Kb=EAb/L,Kp=EAp/L,Kr=EAr/L

(3)

(4)

式中：Kb、Kp、Kr分别为钢梁、压型钢板、楼板内纵向钢筋提供的侧向刚度；E为材料的弹性模量；Ab、Ap分别为钢梁、压型钢板的截面面积；Ar为纵向钢筋的截面面积之和；Ic为边柱的截面惯性矩。

钢筋选用T3D2三维桁架单元，压型钢板选用S4R壳单元，其余部件选用C3D8R实体单元进行建模。进行网格灵敏度分析，经过多次计算确定最适合的网格尺寸，相关部件网格布种尺寸为：钢柱近似40 mm布种；钢梁近似40 mm布种；混凝土板近似30 mm布种；钢筋近似20 mm布种；盖板、剪切板和螺栓等部件均以5 mm布种。在节点断裂位置等应力集中部位进行了密集的网格划分，近似5 mm布种，并与非加密区设置了网格过渡，这既保证了计算的效率，也可以尽可能反映组合梁柱子结构关键区域的受力特性。

1.4 接触关系定义

剪切板和盖板与梁柱截面通过绑定约束模拟焊接连接；钢筋、栓钉与上盖板采用嵌入命令模拟与混凝土板的接触；梁柱节点处剪切板、梁和螺栓等连接部位选用通用接触的方法进行模拟，切向方向接触为库仑摩擦，摩擦因数取0.3，法向接触属性选择硬接触。在螺栓的两侧表面施加均布荷载来模拟螺栓预紧力。在数值模拟过程中，不考虑材料的初始缺陷和焊接残余应力的影响。

2 模型验证

2.1 试验概况

为验证有限元模型及建模方法的正确性，选取文献[23]中的WUFG-S试件进行对比分析。WUFG-S试件为1∶3的缩尺模型，其梁截面的尺寸为HM150×100×6×9，柱截面尺寸为HW150×150×8×10，梁跨长1 500 mm，两边柱长1 100 mm。试件相关材性、各部件及节点详细尺寸参考文献[23]，根据试件尺寸通过ABAQUS软件建立了对应的精细化有限元模型，如图3所示。

图3 有限元模型Fig.3 Finite Element Model

2.2 模拟结果对比

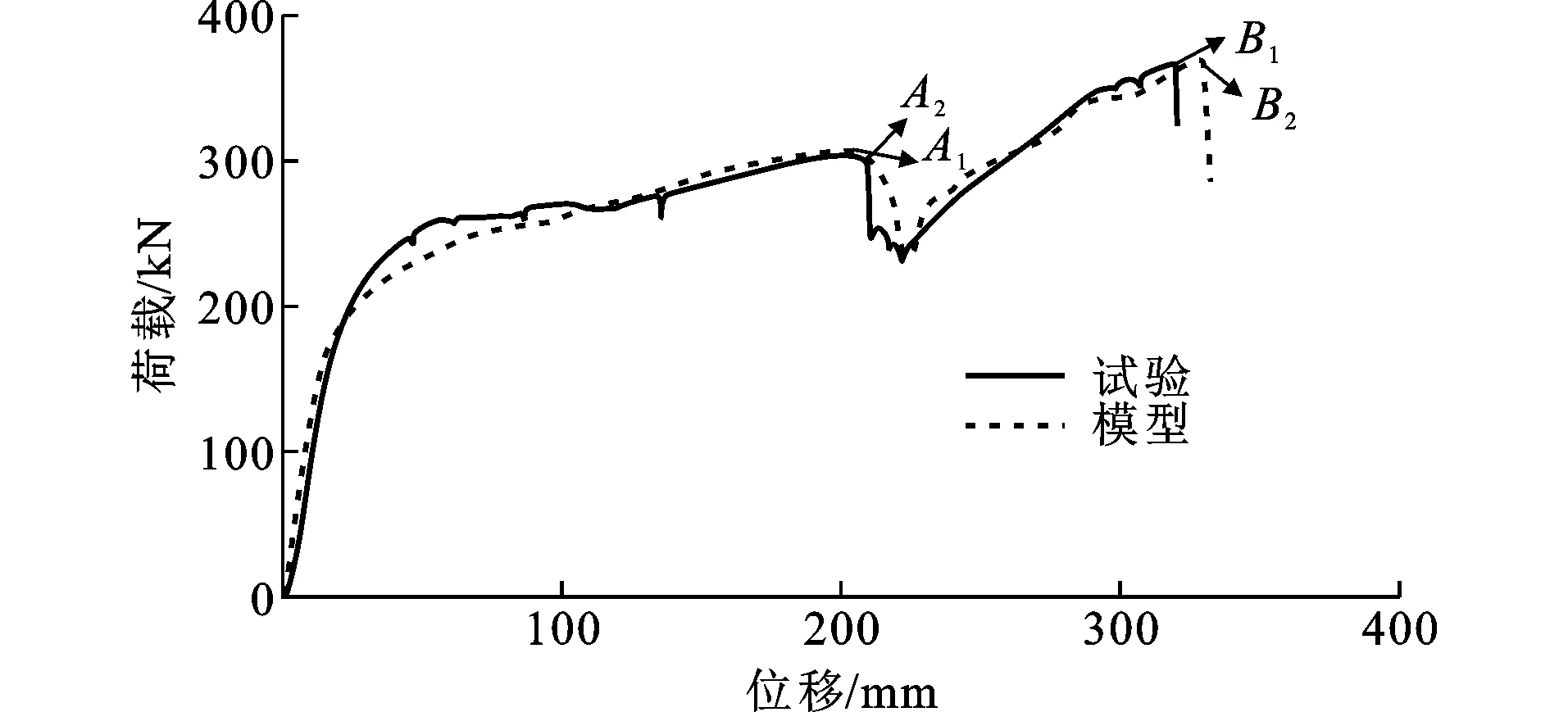
图4 荷载-位移曲线对比Fig.4 Comparison of Load-displacement Curves

图5 破坏模式对比Fig.5 Comparison of Failure Modes

图4为试验与有限元分析的荷载-位移曲线对比。由图4可知，曲线整体发展趋势相同，试件首次断裂点荷载(A1=302 kN、A2=293 kN)相差3%，钢梁完全断裂点荷载(B1=367 kN、B2=360 kN)相差2%，表明有限元模拟的荷载-位移曲线与试验曲线吻合较好。图5为试验与有限元分析的破坏模式对比。由图5可知，数值分析结果与试验的破坏模式相似，表明所建立的有限元模型可准确地模拟出梁柱子结构的破坏过程。综上所述，本文所建立的精细化有限元模型计算结果与试验结果吻合较好，可在此基础上进行后续参数分析。

3 参数分析

基于第1节数值模型的建模方法，建立了足尺模型，研究周边约束、边柱尺寸、边柱轴压比对梁柱子结构抗倒塌能力的影响，分析梁柱子结构的抗倒塌性能。

3.1 边界约束

梁内悬链线机制的抗力主要取决于梁端的有效拉结力和梁端转角，边界约束决定子结构梁端拉结力和梁端转角，故子结构边界约束对其悬链线机制的发展影响显著。梁柱子结构的轴向约束刚度由Kab、Kac和Kas构成，其子结构的简化模型如图6所示。

图6 部分边界约束梁柱子结构简化模型Fig.6 Simplified Model of Beam-column Substructure with Partial Boundary Constraints

引入弹簧约束系数n，n为子结构周边约束构件弹簧的侧向刚度Kas与子结构自身为梁端提供的侧向刚度K(组合梁与边柱提供的侧向刚度)的比值[30]，计算公式见式(5)。梁柱线刚度比k的计算公式见(6)。

(5)

(6)

式中：IB为组合梁的截面惯性矩。

以部分约束子结构为研究对象，按照表1改变子结构有约束侧梁端的侧向刚度，探究有约束侧的拉结强度对子结构抗倒塌性能的影响。

表1 不同侧向刚度的梁柱子结构设计参数Table 1 Design Parameters of Beam-column Substructure with Different Lateral Stiffnesses

3.1.1 不同侧向刚度下荷载-位移曲线分析

图7(a)为不同侧向约束刚度下梁柱子结构模型荷载-位移曲线对比情况。由图7(a)可知，在不同侧向约束刚度情况下曲线中均有2个显著峰值点，这是由于无约束侧钢梁翼缘受拉发生断裂后，荷载发生突降，随着加载位移的不断增大，裂缝沿弧形向上发展，两侧组合梁发生内力重分布，子结构会达到新的峰值点。在位移加载初期(小变形阶段)，曲线无明显差距。

当n=0时，子结构两侧未得到有效拉结，在钢梁受拉翼缘首次断裂后，由于组合梁的悬链线机制未得到发挥，所以子结构后期承载力几乎稳定不变。当有侧向约束刚度影响时，子结构发生首次断裂后，随着位移的增大，梁柱子结构的悬链线机制得到了充分的发挥，组合梁的承载力得到明显提升。随着子结构侧向约束刚度的增大，子结构的首次断裂点荷载增加了36%，位移增加了16%；完全断裂点荷载增加了67%，位移增加了5%。说明子结构边界条件的加强可以提高梁柱子结构的承载力与极限变形能力。当n>1时，侧向约束刚度增强，梁柱子结构的承载力与中柱加载位移增大不明显，说明周边约束的加强只能在一定范围内提高子结构的极限变形和承载能力，但并不能无限提高。

3.1.2 不同侧向刚度下抗力机制曲线对比

图7(b)、(c)为各模型的抗力发展曲线对比。由图7(b)、(c)可知，不同侧向刚度下的子结构抗力机制发展趋势相同，均经历了梁机制、梁机制向悬链线机制转化及悬链线机制阶段。在各子结构第1次发生断裂之前，主要由梁机制提供抗力抵抗外界荷载，悬链线机制发挥的作用有限。子结构首次发生断裂时，梁机制抗力发生突降，悬链线机制提供的抗力逐渐增大。在各子结构第2次断裂后，梁机制提供的抗力再次减小，在子结构整体抗力机制中占比较小，悬链线机制成为主要的抗力机制。

为具体分析倒塌过程中子结构各抗力机制占比，可利用梁机制贡献系数α与悬链线机制贡献系数β来反映子结构各抗力机制的作用占比，α与β可根据式(7)进行计算。

α=PF/P，β=PC/P

(7)

式中：PF为梁机制抗力；PC为悬链线机制抗力；P为总抗力。

图7 不同侧向刚度下的梁柱子结构模型对比Fig.7 Comparison of Beam-column Substructures with Different Lateral Stiffnesses

图7(d)、(e)为各模型子结构的梁机制贡献系数与悬链线机制贡献系数的发展变化情况，在整个梁柱子结构大变形过程中，由初期梁机制阶段向后期的悬链线机制转化，悬链线机制最大可占总抗力的80%。随着周边约束提供的侧向刚度逐渐增大，子结构的悬链线抗力机制贡献系数也相应变大。当n增大时，梁机制抗力最大值增长10%，悬链线机制抗力最大值增长29%，这说明子结构边界条件的加强对梁机制抗力提升较小，但可显著提升子结构的悬链线机制抗力，从而提升子结构的后期承载力。

3.2 边柱尺寸

边柱为梁柱子结构端部提供轴向和转动的约束，故边柱截面尺寸变化会显著影响子结构的边界条件。在子结构承受外界荷载作用时，若边柱提供的刚度不足，则会引发结构水平方向上的连续性倒塌现象，若边柱的尺寸过大，不仅会造成材料的浪费，而且会影响整个结构的安全。为了进一步探究边柱尺寸对子结构抗连续倒塌性能的影响，以梁柱子结构左侧梁端的侧向约束刚度为0与右侧梁端的侧向刚度0.5K为前提，针对次边柱失效情形下的组合梁柱子结构的无约束侧边柱尺寸进行变参分析。

参数设计如表2所示，其中模型只改变边柱尺寸，其他构件尺寸不作变动。

表2 不同边柱尺寸的梁柱子结构参数Table 2 Parameters of Beam-column Substructure with Different Side Column Sizes

3.2.1 不同边柱尺寸荷载-位移曲线分析

图8(a)为不同边柱截面尺寸情况下各模型的荷载-位移曲线对比。由图8(a)可知，各模型荷载-位移曲线发展趋势相似，且均具有2个荷载峰值点。在位移加载初期，各模型子结构的荷载-位移曲线相差不大，随着加载位移的逐渐增大，子结构的首次峰值点和二次峰值点差异显著。当梁柱线刚度比在一定范围内减小时，结构的首次断裂点和完全断裂点荷载分别增加了14%和34%，说明边柱尺寸的增大可以提高子结构整体的承载能力，但是当子结构梁柱线刚度比过于小时，子结构的承载能力不再增加。这是因为边柱尺寸过大时，边柱的节点域几乎不再发生转动，梁的变形主要体现在弯曲变形上，而子结构后期的承载力主要由梁内轴拉力提供，通过梁受弯而形成的抗力不再增大，故此时边柱尺寸的影响不大。如果子结构边柱尺寸过大，对其结构整体抗倒塌的承载力提升不明显。梁柱线刚度比值在0.6～1.1时，梁柱构件可协同作用使子结构具有较大的承载能力和变形能力。当模型子结构梁柱线刚度较为接近时，各模型子结构可最大限度地发挥整体的抗倒塌能力。

3.2.2 不同边柱尺寸抗力机制曲线对比

图8(b)、(c)为各模型子结构抗力发展曲线对比，从图8(b)、(c)可以看出，不同边柱截面尺寸的子结构均经历了梁机制、梁机制向悬链线机制转化及悬链线机制3个阶段。在子结构首次断裂后，悬链线机制抗力逐渐成为总抗力的主要部分，而对于梁柱线刚度比处于0.6～1.1的子结构，随着线刚度比的减小，梁机制抗力最大值增长约10%，悬链线机制抗力最大值增长约35%，说明边柱可为梁端提供有效的轴向与转动约束，有利于梁内悬链线机制的发挥。

图8(d)、(e)为各模型子结构抗力贡献分配情况。随着边柱的截面尺寸逐渐增大，子结构的悬链线抗力机制贡献系数也相应变大，说明子结构边柱有效的拉结作用可显著提升子结构的悬链线机制抗力，进而提升整体的极限承载能力。模型WUFG-Sa的悬链线抗力机制贡献系数滞后其他子结构许多，说明边柱刚度过弱，边柱会先于组合梁发生破坏，限制悬链线机制的发挥，进而降低结构的整体抗倒塌能力。

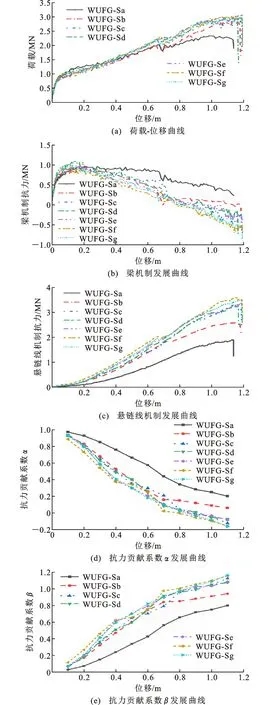
图8 不同边柱尺寸的梁柱子结构模型对比Fig.8 Comparison of Beam-column Substructures with Different Side Column Sizes

3.3 边柱轴压比

在选取内部的子结构进行抗倒塌能力的研究时，通常会通过对边柱施加一定的轴压比模拟上部结构的荷载作用。为分析轴压比对子结构抗倒塌性能的影响，基于子结构试验的边界条件，以部分约束组合梁柱子结构为研究对象，探究不同轴压比对梁柱子结构抗倒塌能力的影响程度。梁柱子结构的轴压比参数如表3所示。

3.3.1 不同边柱轴压比荷载-位移曲线对比

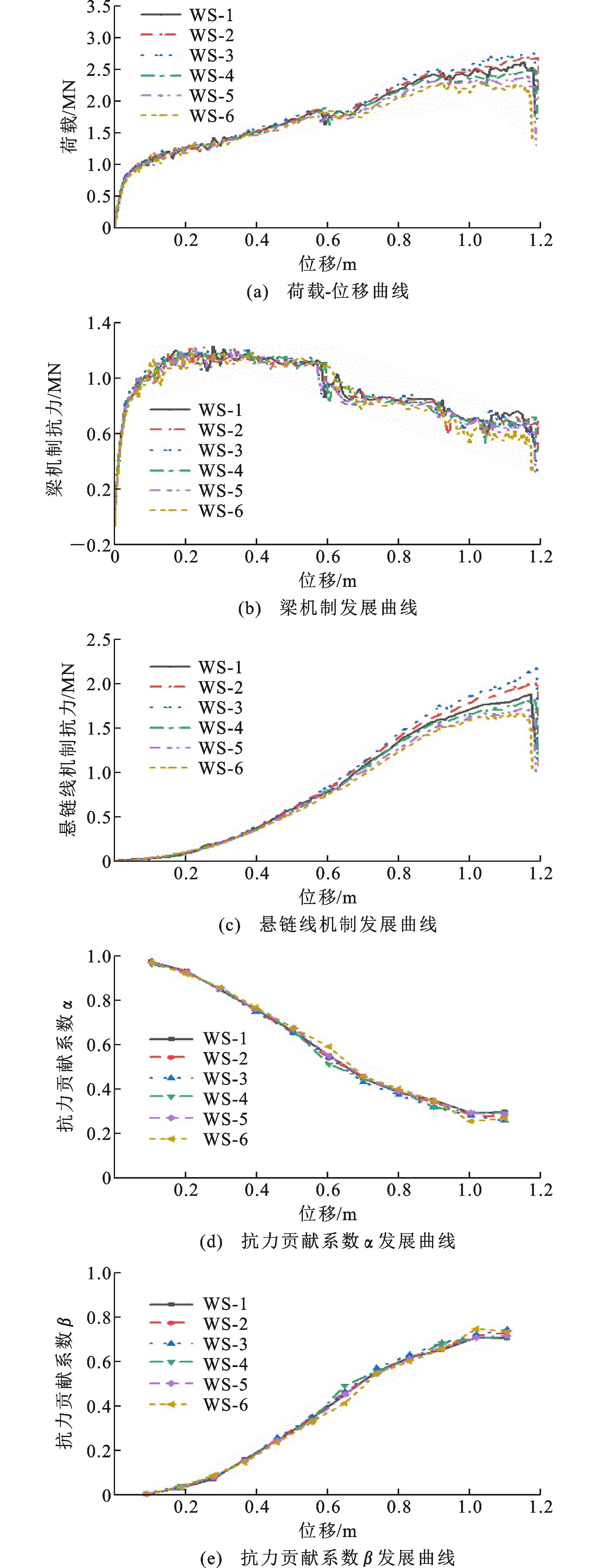
图9 不同轴压比的梁柱子结构模型对比Fig.9 Comparison of Beam-column Substructures with Different Axial Compression Ratios

图9(a)为不同边柱轴压比下梁柱子结构模型的荷载-位移曲线对比，由图9(a)可知，模型WS-3的二次完全断裂处峰值荷载与模型WS-1、WS-2相比分别升高约8.5%和3%。轴压比过小时，边柱的节点域随着两侧梁的变形而发生转动，从而限制组合梁内竖向抗力的发挥，降低整体的承载力，与模型WS-3相比，WS-4、WS-5、WS-6的二次峰值荷载分别降低了8.5%、13%、22%。次边柱失效后的剩余子结构有一侧无水平的侧向拉结，当边柱上施加荷载过大时，会降低边柱的刚度，影响子结构的抗倒塌承载能力。

表3 轴压比设计参数Table 3 Design Parameters of Axial Compression Ratio

3.3.2 不同边柱轴压比抗力机制曲线对比

图9(b)、(c)为各子结构抗力发展曲线对比，在悬链线机制发展曲线中，轴压比为0.3的子结构提供的悬链线机制抗力最大，此时子结构周边的边界条件最大程度地保证悬链线机制抗力的充分发展。对于轴压比小于0.3的模型WS-1和WS-2，由于边柱轴向荷载施加有限，发生破坏时过小的轴压比会使无拉结端边柱无法提供合适的侧向约束刚度，限制了梁内竖向抗力的发展，导致提供的悬链线机制抗力有限。对于轴压比大于0.3的模型WS-4、WS-5和WS-6，由于边柱轴向荷载过大，在轴向荷载和梁端的水平拉结作用下会降低边柱的刚度，限制了梁内悬链线机制抗力的发展。

图9(d)、(e)为各模型子结构的梁机制贡献系数与悬链线机制贡献系数的发展变化情况。可以看出，不同轴压比情况下子结构的梁机制贡献系数和悬链线贡献系数差别不大，轴压比对于子结构抗力机制的占比情况影响较小。

4 结 语

(1)随着梁端侧向刚度的逐渐增大，不同侧向刚度下的子结构破坏模式类似，均是在无侧向约束端钢梁下翼缘首先发生受拉断裂，而有侧向约束端钢梁下翼缘未发生任何断裂。当n<1时，提高梁柱子结构的侧向约束刚度可以提高子结构的悬链线机制抗力，进而提高子结构的后期承载力。

(2)边柱尺寸过小容易引发柱的弯曲破坏，限制后期悬链线机制抗力的发展，进而降低子结构后期极限承载力。边柱尺寸过大时，增大边柱尺寸对提升结构的承载力影响有限，不仅会造成材料的浪费，而且会影响整个结构的安全。对于梁柱线刚度比处于0.6～1.1的子结构，边柱可为梁端提供有效的轴向与转动约束，此时梁柱线刚度比减小有利于梁内悬链线机制的发挥，进而提升子结构整体的抗倒塌性能。

(3)轴压比对结构后期抗倒塌承载能力具有一定的影响。当轴压比小于0.3时，随着轴压比的增大，结构后期承载能力不断增大；轴压比大于0.3时，边柱顶部所承受的竖向荷载较大，在边柱中部水平拉结和柱顶竖向荷载共同作用下导致边柱刚度降低，不利于梁内悬链线机制抗力的发展，进而降低子结构的后期承载力。