性能参数对混凝土柱破坏指数的影响

2022-06-07吴守军

建筑科学与工程学报 2022年3期

付国，何斌，吴守军

(西北农林科技大学水利与建筑工程学院，陕西杨凌 712100)

0 引言

强震作用下结构的抗震性能优劣关乎人民群众生命安全，依据破坏准则预测主要抗侧力构件特别是混凝土柱的性能退化程度一直是抗震研究的热点问题，对实现大震不倒设防目标具有重要意义[1-5]。已有破坏准则通过探索构件破坏过程中变形、荷载、耗能等性能参数变化规律，研究极限状态下破坏指数与破坏现象的对应关系[6-9]。

抗震规范[6]和基于性能的抗震设计方法[10]均通过比较位移角与预设构件极限值判断其破坏程度，位移角和变形参数虽然在测量、计算方面具有显著的优势，但对不同变形能力的构件采取同一判定指标是不合理的。滞回耗能不仅与构件变形能力相关，还受加载制度影响较大。试验表明不同加载幅值下构件破坏所需的总滞回耗能存在较大差异[11]，拟静力试验中加载循环次数对承载力、极限变形、总滞回耗能均具有显著影响[12]。由于构件变形能力的差异，以变形、耗能为代表的单参数破坏准则不仅需要更多的试验验证以实现安全性与经济性的平衡，还应考虑加载制度、设计参数等因素的影响。

部分学者探索多参数组合的量化方法定义构件破坏，其中考虑首超破坏和累积耗能影响的Park-Ang双参数准则应用最为广泛[13-14]。Park-Ang准则中组合参数β和极限状态下的破坏指数也是后续研究和改进的重点[15-17]。由于破坏过程中变形与耗能2个参数之间存在复杂耦合关系，如何解释和量化这种耦合关系是双参数准则合理、准确与否的关键。

基于疲劳理论提出了混凝土柱的等效延性破坏准则[11]，实现了单调加载与反复加载破坏准则表达式的统一。深入的试验数据统计分析还发现延性系数的平方与总滞回耗能存在近似比例关系，考虑构件的极限变形能力大小与倒塌破坏之间的关系和轴压比、配箍率、承载力退化程度对混凝土柱破坏的影响，提出混凝土柱的改进延性破坏准则[18]。综合破坏准则计算结果、性能参数变化规律与试验现象对应关系，讨论何种性能参数更适合应用于破坏准则研究，并对不同破坏准则的合理性进行分析以提升混凝土柱的抗震性能量化水平。

本文通过对比位移角与位移角限值的比值、承载力与峰值承载力的比值、反复加载下变形与单调加载下极限变形的比值同双参数准则、延性准则破坏指数之间的变化规律，分析性能参数、破坏指数与破坏现象的对应关系，研究性能参数选取对破坏指数计算结果的影响，探讨考虑变形能力极限的延性准则合理性。

1 性能参数与破坏准则

1.1 位移角比值

抗震规范完成了大量构件和框架模型试验的统计分析，建议混凝土框架层间位移角限值[θp]为1/50，并留有一定安全储备[6]。定义混凝土柱的位移角限值与层间位移角限值相同，位移角与位移角限值的比值dθ由式(1)计算得出。

(1)

式中：θ为反复加载下柱极限位移角。

考虑混凝土强度、配箍率、配筋率、轴压比、加载制度等设计参数的不同，不同延性混凝土柱位移角达到1/50时柱抗震性能存在较大差异[7-8]，破坏时的极限位移角也具有显著不同。

1.2 承载力退化值

混凝土柱承载力下降至无法满足上部结构需求时破坏不可避免，受场地限制和试验设备安全性要求，模型试验多选取承载力加速下降或达到某一特定值[3,9](多为极限承载力的85%)作为极限状态，参考位移角比值计算方法，承载力退化值dF计算式为

(2)

式中：F为反复加载下柱破坏时的承载力；Fmax为柱的峰值承载力；当构件承载力未达到峰值承载力时，混凝土柱未发生倒塌破坏，dF=0。

1.3 变形能力值

借鉴双参数准则[13-14]研究成果，把单调加载下混凝土柱极限变形对应的延性系数定义为最大变形能力值μmax，μ为反复加载下位移幅值对应延性系数，变形能力值dμ的计算式为

(3)

变形能力值越大，柱的塑性变形发育越充分，越接近破坏极限状态，已有试验表明反复加载对应变形能力值dμ<1.0，单调加载时变形能力值dμ=1。

1.4 双参数破坏准则

双参数破坏准则计算式为

(4)

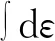
考虑大多数试验中未设置单调加载条件下的对照试验，由式(5)计算得出μmax，即

(5)

式中：Ls为柱的计算长度；δy为混凝土柱的屈服位移；θust为单调加载下矩形截面混凝土柱的极限转角。

θust由计算式(6)[19]得出，即

(6)

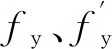
把单调加载视为位移幅值为Δmax、加载循环次数为1/4的反复加载，则Δmax为1/4次反复加载下混凝土柱的最大变形[11]。从这个角度看Park-Ang准则变形项对变形能力强弱进行了思考：单调加载变形越大表明柱的变形能力越强，加载制度、位移幅值相同时变形能力强的构件破坏程度更小，继续抵御地震作用的能力越强，破坏指数也越小。

耗能项未能延续考虑变形能力影响的设计思想，Qy和δμ的组合能否定义为构件的最大耗能仍需更多研究，受加载制度、构件响应不确定性的影响，确定柱的最大耗能对双参数准则的改进和延续变形能力强弱的设计思想具有重要意义。

1.5 延性破坏准则

考虑相同设计参数、加载幅值情况下变形能力强的柱破坏更轻微，继续抵御地震动作用的能力也越强，变形能力强弱理应作为一个关键参数在破坏指数计算中予以考虑。参考双参数准则中变形项δm/δμ的表达式，结合拟静力试验结果，本文定义柱的最大变形为单调加载下的极限变形，即混凝土柱的最大变形能力值。

等效延性准则研究表明延性系数既定义了构件的变形大小，还可以定量描述构件的塑性变形发育程度，理论上更适宜作为破坏准则的分析参数；试验数据统计结果还表明延性系数平方与总耗能值存在近似比例关系，因此选择延性系数作为延性破坏准则的性能参数，考虑构件变形能力、轴压比和配箍率的影响建立了混凝土柱延性破坏准则[18]，计算公式为

(7)

kn=22n-0.3

(8)

kρv=1.28e-0.1/ρv

(9)

式中：βi为计算位移幅值下的加载循环次数；μi为第i个加载幅值对应的延性系数；kn为轴压比影响系数；kρv为配箍率影响系数；ρv为配箍率。

延性准则不仅考虑了轴压比、配箍率、加载制度等对变形能力有显著影响的参数，还引入了单调加载延性系数，重点探索了变形能力大小对结构抗震性能的影响规律。与等效延性准则类似，延性准则同时适用反复加载与单调加载，实现了破坏准则计算公式的统一，探索了变形能力强弱与构件破坏变形之间的影响规律。

2 混凝土柱试验数据

2.1 文献来源与模型编号

为研究破坏指数计算中设计参数的影响规律，选取43根弯曲型破坏为主的混凝土柱进行计算研究，各试件编号与文献来源见表1。

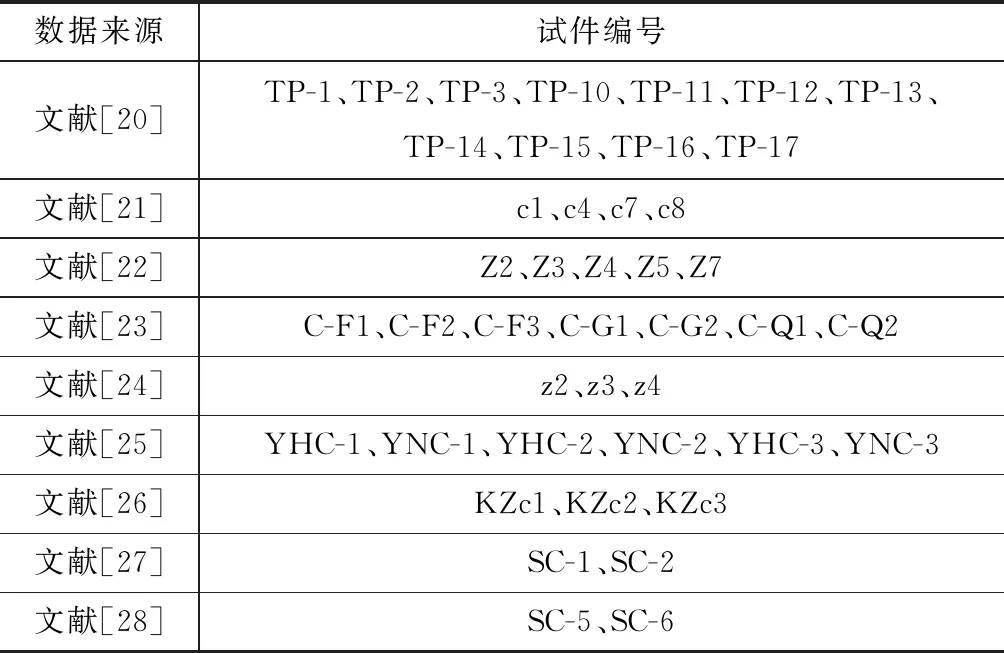
表1 混凝土柱编号Table 1 Numbers of Concrete Columns

表1中柱的混凝土强度分布区间为21.5～43.5 MPa，纵筋配筋率为0.62%～4.29%，体积配箍率为0.56%～1.71%，剪跨比为3.0～4.0，轴压比为0.04～0.50，具体参数见对应参考文献。

2.2 破坏指数计算结果

试验研究和理论分析多选取承载力下降至某一特定值作为柱的破坏临界点或试验加载终止点，承载力退化越严重的柱破坏程度和破坏速度也越大，为更好地研究破坏指数与承载力退化的相互关系，假定承载力退化最大值与破坏指数满足式(10)。

(10)

式中：dμmax为承载力退化最大值；Dμ为混凝土柱倒塌极限状态对应的破坏指数；D0.85为混凝土柱承载力退化至最大承载力85%时对应的破坏指数。

混凝土柱的性能参数和破坏指数计算结果、承载力退化值85%对应的破坏指数计算值见表2。由表2可知，混凝土柱达到破坏极限时位移角比值的平均值为1.951，标准差为0.524，表明不同延性构件的破坏极限具有显著差异。承载力退化值为0.614，远小于85%试验建议值，选择85%峰值承载力作为构件破坏临界状态同样具有一定的安全冗余度，标准差为0.176，承载力退化值离散性显著低于位移角比值。

变形能力值的平均值为0.712，标准差为0.104，表明混凝土柱破坏过程中变形能力值变化最小，选取单调加载极限变形为柱极限变形能力具有离散性低的显著优势。

表2 破坏指数计算结果Table 2 Calculation Results of Damage Index

双参数准则破坏指数平均值为1.268，延性准则破坏指数平均值为1.147，更接近1.0，与试验现象更为吻合。承载力退化至85%峰值承载力时破坏指数计算表明，双参数准则对应破坏指数的平均值为0.946，延性准则对应破坏指数的平均值为0.798。根据试验现象和破坏规律，混凝土柱承载力退化至85%峰值承载力时未达到倒塌破坏极限状态，破坏指数也远小于1.0，延性准则与试验现象吻合更好。

需要指出的是Park-Ang双参数准则中的计算式是基于20世纪80年代的混凝土柱数据统计得出的，受混凝土强度、钢筋用量、轴压比等参数的取值影响，得出的β值和破坏指数均显著偏大。

3 破坏指数与性能指标

3.1 性能参数间的相关系数

混凝土柱破坏越严重，位移角比值越大，承载力退化值就越小，极限位移越接近单调加载极限位移，对应的破坏指数与性能参数之间的相互关系应符合上述规律。为了研究不同性能参数与破坏指数之间的相关系数，借助EXECL软件中的Correl函数进行了研究，计算公式为

(11)

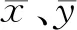
根据表2数据重点分析了位移角比值、承载力退化值和变形能力值3个参数与双参数破坏准则、延性准则之间的相关系数，计算结果见表3。

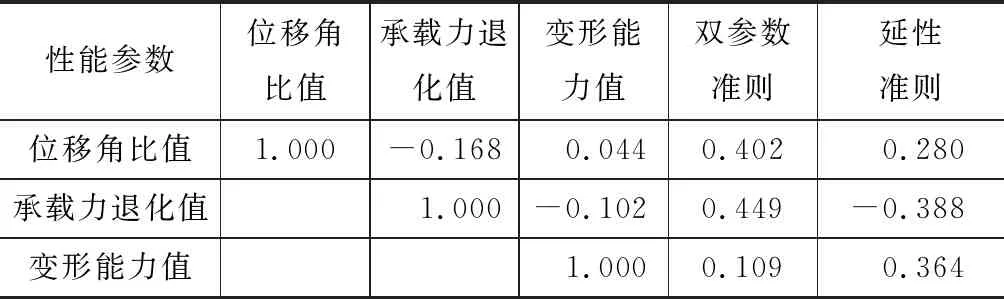
表3 破坏指数与性能参数的相关系数Table 3 Correlation Coefficient of Damage Index and Performance Parameters

位移角比值和承载力退化值的相关系数为-0.168，位移角比值与变形能力值的相关系数为0.044，变形能力值与承载力退化值的相关系数为-0.102，变形能力值与其余参数的相关性最低。

位移角比值、变形能力值与承载力退化值的相关系数为负，与柱破坏越充分承载力退化越严重，变形越大且越接近单调加载极限变形的规律相符。变形能力值与位移角比值的相关系数为正，表明随着变形的增加，变形能力值越大。两者相关系数仅为0.044，说明柱的塑性变形发育程度与破坏之间的关系更为密切。

考虑不同构件破坏时极限值的显著差异，选取上述参数的某一阈值直接定义混凝土柱破坏很难兼顾安全性与经济性。

3.2 性能指标与破坏准则的相关系数

双参数准则破坏指数与位移角比值的相关系数为0.402，与变形能力值的相关系数为0.109，与承载力退化值的相关系数为0.449。

反复加载下的极限承载力与峰值承载力的比值越小，柱破坏越严重，对应破坏指数应越大，两者之间应为负相关，双参数准则破坏指数与承载力退化规律及试验现象存在较大差异。试验研究和理论分析表明，柱变形是否接近其理论最大变形较变形大小对破坏的影响更为显著，双参数准则与变形能力值的相关系数较小，与破坏规律存在偏差。

延性准则破坏指数与位移角比值、承载力退化值、变形能力值的相关系数分别为0.280、-0.388和0.364。计算结果表明延性准则与位移角比值的线性相关性低于变形能力值的相关性，与承载力退化值负相关，符合构件破坏规律，受承载力退化和变形能力对破坏影响显著，延性准则与破坏规律吻合更好。

综上所述，双参数准则不能合理反映柱破坏加剧与承载力退化值减少的规律，破坏指数与变形能力值的相关性较低。延性准则与3种性能指标的线性相关性更为合理，能够更好地解释不同构件的塑性变形发育程度、变形能力强弱对倒塌破坏的影响。

3.3 性能指标与破坏指数关系曲线

延性准则计算结果表明：承载力退化值变化规律为迅速增大至峰值承载力(退化值为1.0)，承载力逐渐开始下降，破坏指数增大；变形能力值对应破坏曲线的变化规律为单调递增，构件破坏过程中变形能力值不断增大，破坏指数递增。43根混凝土柱的破坏曲线如图1所示。

图1 混凝土柱破坏曲线Fig.1 Failure Curves of Concrete Columns

由图1破坏曲线可知：混凝土柱的承载力退化值越小，变形能力值和破坏指数也就越大，破坏越充分，延性-变形能力值曲线斜率逐渐变小，承载力退化和破坏指数总体上呈加速状态；越接近破坏极限状态，柱的破坏速度越快，变形能力值越大，但变形能力的增速变缓，对应曲线斜率越小；承载力退化值在破坏过程中存在波动现象，对破坏指数计算存在不利影响，且柱破坏时承载力退化值的离散性较大。

变形能力值从供、需2个层面对构件性能退化程度进行量化，对应破坏曲线能更好地解释柱的破坏规律和破坏过程，变形能力值较变形(位移角)、承载力退化值更适宜作为倒塌破坏分析参数。