深部圆形隧道围岩分区破裂的简化梯度模型
2022-06-07贺子光赵法锁陈昊祥周静静
贺子光,赵法锁,陈昊祥,吴 博,周静静
(1.黄淮学院 建筑工程学院,河南 驻马店 463000;2.长安大学 地质工程与测绘学院,陕西 西安 710064;3.北京建筑大学 北京市工程结构与新材料工程研究中心,北京 100044;4.信息产业部电子综合勘察研究院,陕西 西安 710054)
由于特殊的变形破坏模式,分区破裂化作为深部围岩典型的非线性力学现象自被发现以来便受到了广泛关注[1-6]。经过40 余年的研究,在理论分析、试验以及数值模拟等方面都取得了一定的成果。但关于围岩分区破裂化形成机理的研究,仍然是一个尚未完全解决的问题。E.I.Shemyakin 等[4]认为破裂区的形成是由于支撑压力区在环向应力作用下,径向应变超过极限而发生劈裂破坏所致。M.A.Guzev 等[7]采用非欧几何与非平衡热力学模型,分析了含缺陷岩石介质的变形破坏问题以及围岩分区破裂化现象。周小平等[8]通过自由能密度、平衡方程以及变形非协调条件,确定了圆形隧道围岩的应力场,认为应力场的波动特性是引起围岩分区破裂化的原因。戚承志团队[9-14]在梯度理论的框架下,考虑岩体进入塑性阶段后的能量耗散和自组织现象,详细地分析了圆形隧道围岩的分区破裂化现象。王明洋等[15]从能量的角度出发,结合统计物理学,分析深部围岩在准定常场与扰动场相互作用下的变形与运动规律,建立了分区破裂化的计算方法。上述学者从不同角度研究了围岩分区破裂化的产生机理,文献[6,16]对深部围岩分区破裂化的研究进展进行了详细阐述,并利用弹塑性理论、断裂力学理论、非线性科学理论等对分区破裂化现象形成的机理进行了探索,从试验和数值模拟2 种手段再现了分区破裂化现象的一些主要特点。但需要指出的是上述研究对于分区破裂化现象的定量表述尚不能令人满意。
内变量梯度理论[17-18]是研究分区破裂现象的方法之一,引入了描述材料内部结构的特征尺度,在解释固体材料的尺寸效应、变形局部化以及空间变形模式等方面显现出了独特的优越性和适应性。该理论采用应变梯度或者其他内变量梯度作为额外的模型变量,将这些梯度变量引入到介质的平衡方程或者内变量演化方程中,可得到不可逆变形的局部化解或者空间分布解。
在分析相关研究成果的基础上,笔者提出采用内变量梯度理论来研究分区破裂现象,可得到圆形隧道围岩中应力场和变形场的封闭解析解,并进行理论与试验对比结果,验证提出方法的可靠性,以期为定量描述分区破裂化现象提供一种新的方法手段。
1 内变量梯度模型
在长期的地质构造作用下,岩体被内部的微裂纹、节理裂隙以及断层破碎带等不同尺度的结构面分割成了不同尺寸的岩块,由于内部结构面和缺陷分布的复杂性与随机性,造成了岩体材料的非连续性、非均匀性以及力学性质的离散性。岩体的变形和破坏主要表现为宏观力学特性的变化,而深部岩体的宏观力学特性主要由应力水平与内部(微观)构造层次决定。长久以来,材料物理学家及力学家拟通过研究材料的微观特性来确定材料的宏观特性,但众多的尝试都难以实现既定目标。初期认为失败的原因是描述材料变形破坏的数学手段的复杂性所造成,但长期深入研究发现,一方面是对于材料变形的认识不正确;另一方面是材料内部包含着众多的结构层次所致[19]。
由于内部结构层次的存在,在外力场的作用下,岩石材料的变形与应力分布复杂而紊乱,并伴随有应力集中、应变局部化以及非协调变形等现象。在笔者的前期工作中[20-21],采用简化的内变量梯度模型,很好地解释了圆孔问题的尺寸效应,且该模型形式简单、物理意义明确。基于上述原因,本文将采用下式所示模型研究围岩分区破裂化现象。
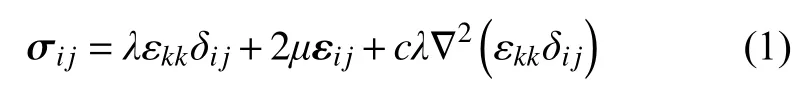
式中:σij为应力张量;εij为应变张量;λ、μ为拉梅常数;c为梯度系数,c=l2(l为材料内檩长度);δij为Kronecker 符号;∇2为拉普拉斯算符;εkk为体应变。关于此模型的理论推导可参考文献[22]。
观察式(1)可以发现,本文提出的内变量梯度模型的物理本质为经典胡克定律的扩展,沿用了胡克定律中关于材料均匀、连续和各向同性的假定。区别在于本文提出的内变量梯度模型引入了材料体应变的梯度项此项用于描述材料微观结构对其宏观力学行为的影响,具体的物理学动机和意义详见文献[23]。
深部圆形隧道可简化为轴对称平面应变问题,力学模型如图1 所示。

图1 圆形隧道力学模型Fig.1 Mechanical model for circular tunnels
此时,式(1)可化为极坐标形式:
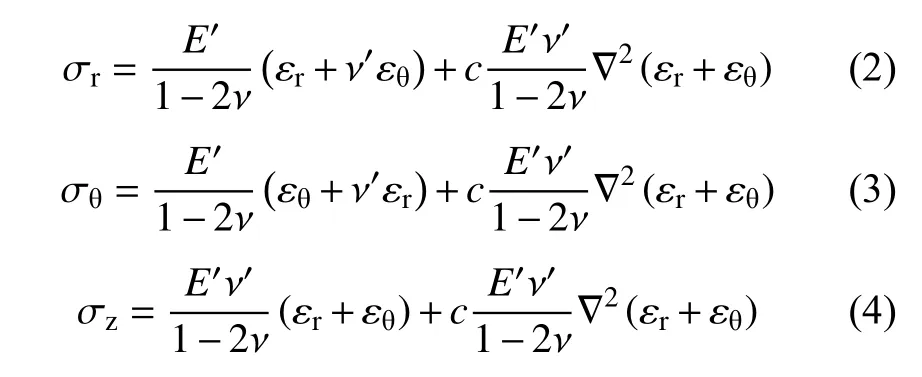
式中:σr、σθ和σz分别为径向、环形和轴向应力分量;E′=E(1−ν)/(1+ν),ν′=ν/(1−ν),E为岩石的弹性模量;ν为泊松比;εr为径向应变;εθ为环向应变。
由对称性可知,围岩仅产生径向位移ur,此时几何关系可简化为:
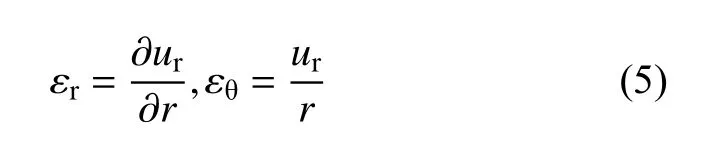
如果体力忽略不计,则平衡方程可化为:
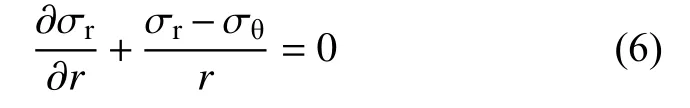
将式(2)−式(5)代入式(6)可得一个关于ur的四阶常微分方程,求解该方程可得:
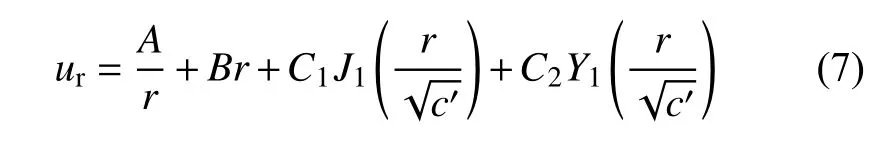
式中:c'=cν';J为第一类贝塞尔函数;Y为第二类贝塞尔函数;下标表示阶数;A,B,C1,C2为积分常数。
为了确定式(7)中的积分常数,需要4 个边界条件,除了经典的应力边界条件σr|r=a=0,σr|r→∞=σ0以外,仍需2 个其他边界条件。其他边界条件的物理本质为位移边界条件,其具体形式[18,22]可表示为:

将积分常数代入式(7)可得围岩的位移场:
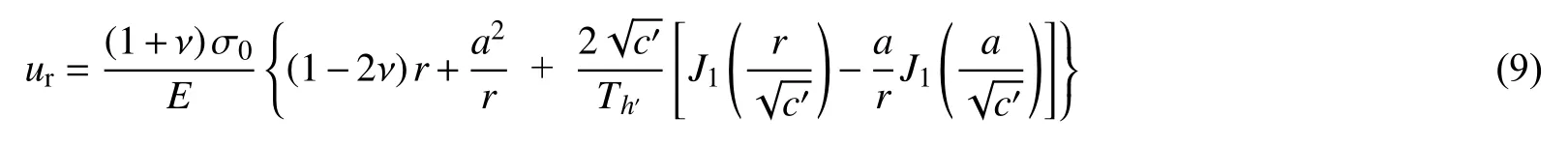
由式(9)所示位移场可知,围岩的应变场为:

需要注意的是,地下隧道开挖前围岩处于预压状态并已产生初始位移:
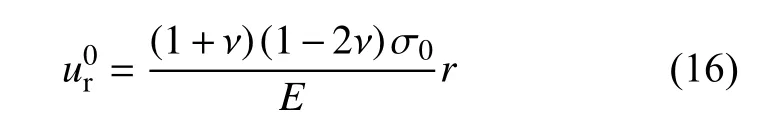
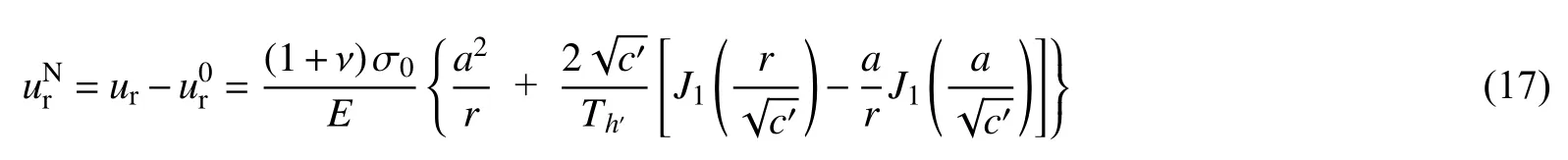
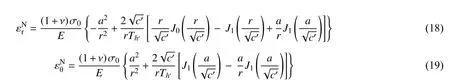
2 应力与变形场的分布及参数敏感性分析
为了研究隧道周围应力与变形场的分布情况以及梯度系数的敏感性,参考实际案例和参数取值经验,各参数值选择如下:隧道开挖半径a=2.5 m,远场应力σ0=40 MPa,围岩的弹性模量与泊松比分别为E=20 GPa,ν=0.25。理论计算结果如图2−图4 所示。
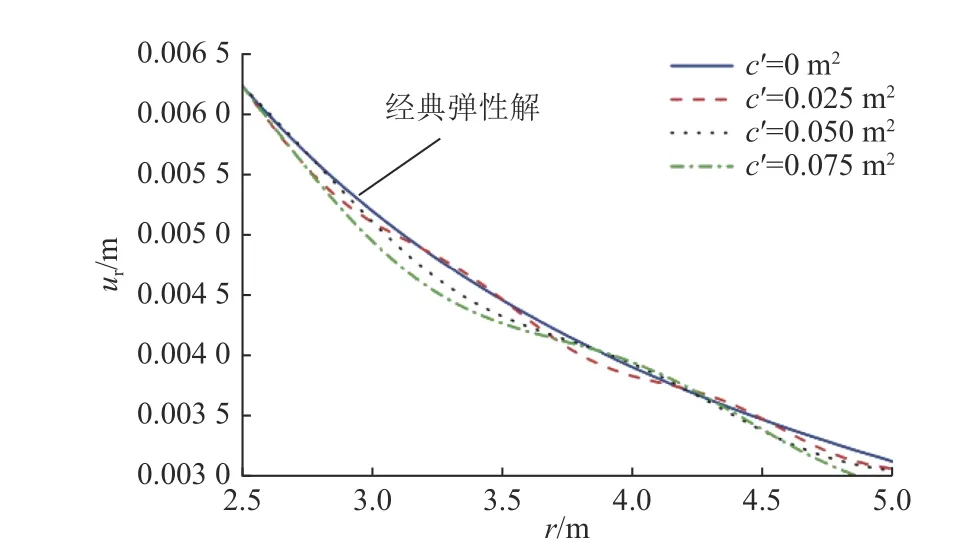
图2 深部圆形隧道围岩位移场ur 分布曲线Fig.2 Distribution of the radial displacement field around circular tunnels
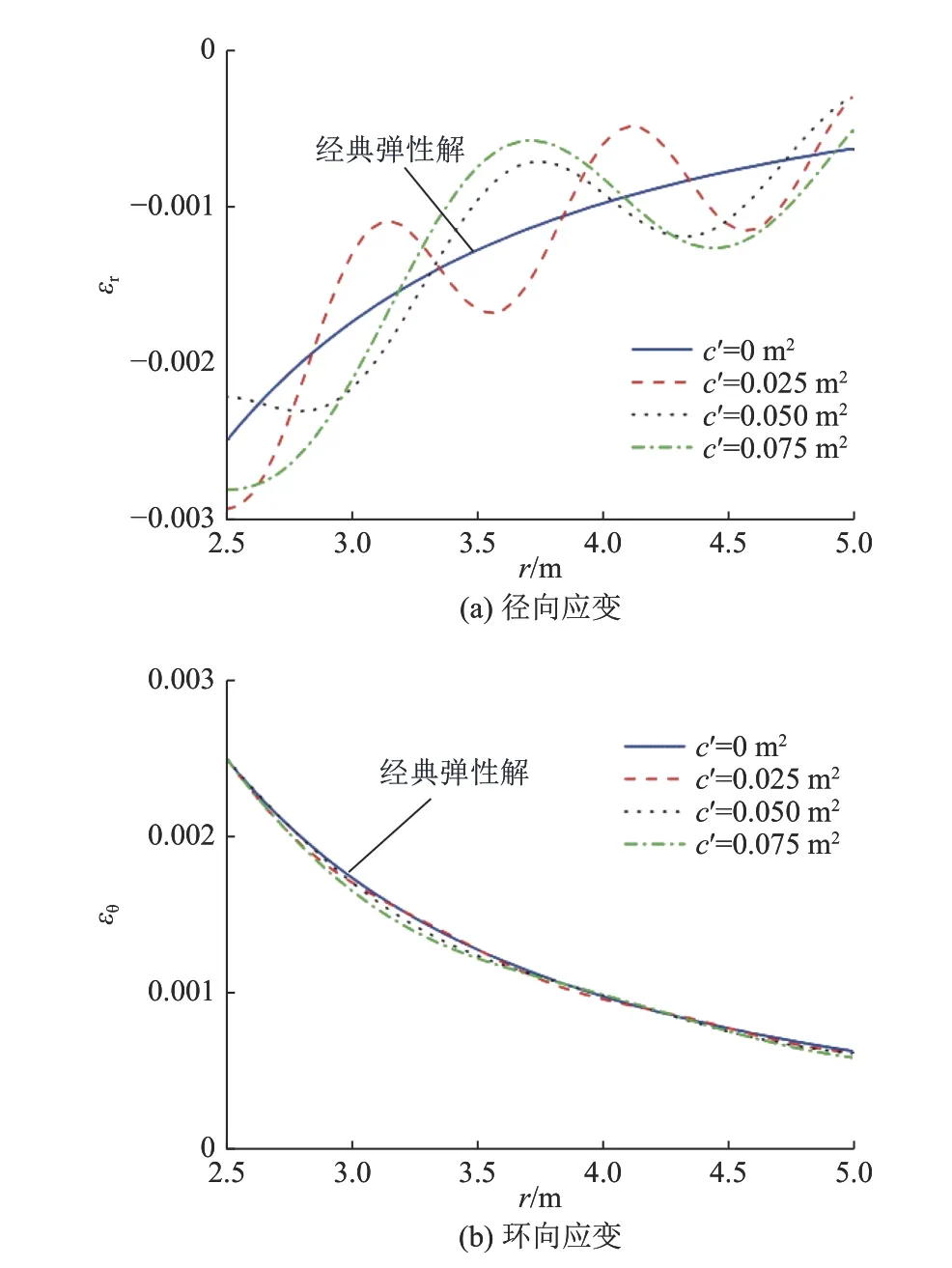
图3 深部圆形隧道围岩应变场分布曲线(受压为正)Fig.3 Distribution of the strain field around circular tunnels
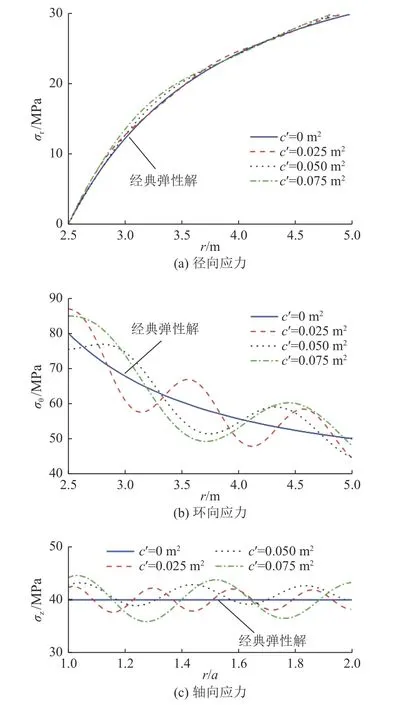
图4 深部圆形隧道围岩应力场分布曲线Fig.4 Distribution of the stress field around circular tunnels
由图2−图4 可知,提出的梯度模型求得的应力场和变形场以经典弹性解为基准上下波动,表现出准周期性和波动特性,且随着梯度系数c'的增大,解的准周期性和波动特性越显著。梯度系数c'取值越大,表明材料内部微观结构的尺度越大,此时微观结构对材料宏观力学性能的影响越显著。当梯度系数c'=0 时,梯度模型退化为经典弹性理论。梯度模型求得的变形场与应力场的波动特性为理论解释围岩分区破裂化提供了一种可能。
本文提出的梯度模型形式简单,物理意义明确,仅包含一个未知参数,即梯度系数。关于材料梯度系数(或内檩长度)的确定,通常情况下需与材料的尺寸效应、表面能效应、剪切带宽度以及刻痕深度等联系,再结合试验数据加以确定,具体可参考文献[24]。但由于岩石材料的特征尺寸包含从地质构造级别一直到微晶体级别各个层级,在不同地应力水平与几何条件下激活的特征尺度也不尽相同,因此,确定岩石材料梯度系数最可靠的方法是将梯度系数联系到分区破裂的周期或破碎区宽度,然后通过拟合试验或实测数据来确定。
3 理论预测与试验结果对比分析
为了验证本文理论的准确性,需要与试验结果进行对比。由于在实际操作中围岩内部的应力场很难测量,而径向位移的测量相对容易,故本文选取文献[25]中的位移场试验数据进行对比。
文献[25]中试验选取新型铁晶砂胶结岩土相似材料,模型的几何尺寸与应力比均采用1∶50 的缩比,此时施加的应力约为相似材料抗压强度的2 倍,相似材料的具体参数见表1。

表1 岩土相似材料的物理力学参数[25]Table 1 Physical and mechanical parameters of geotechnical similar materials[25]
参数选取如下:隧道开挖半径a=2.5 m,围岩的弹性模量与泊松比分别取E=260 MPa,ν=0.26,梯度系数c=0.25 m2,远场应力分别取σ0=4、5、6 MPa。由式(17)计算可以得到围岩的位移场,理论计算与试验结果对比如图5 所示。
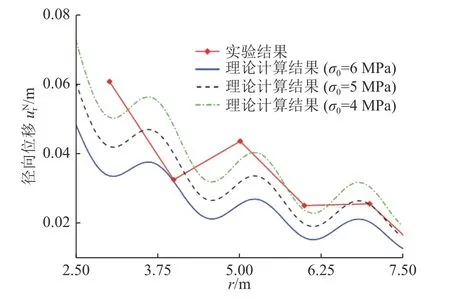
图5 理论计算位移场与试验结果对比Fig.5 Comparison between theoretical prediction and experimental data
比较图5 可以发现,理论曲线与试验结果拟合程度很好,整体上理论结果较试验结果偏小。但理论计算求得的径向位移的波动周期、波峰波谷的位置以及幅值大小都与试验结果基本吻合,可以很好地描述圆形隧道周围的位移场,也证明了理论模型的正确性。
需要指出的是,本文采用的理论模型认为隧道为平面应变问题,而试验则是在三维受力状态下进行。与三维受力状态相比,平面应变状态相当于在轴向施加了一个变形约束,从而提高了围岩的刚度同时也限制了围岩的径向位移。轴向约束虽然会使围岩的径向位移减小,但并不会影响径向位移的波动周期以及波峰波谷的位置。笔者认为上述理由是造成理论预测低于试验数值的主要原因。
4 破碎区位置及宽度的估算
由式(13)−式(19)可知,圆形隧道围岩中变形场与应力场的分布,为了进一步估算围岩破碎区的位置及宽度,需要确定围岩满足的屈服准则。此处,假设围岩服从Mohr-Coulomb 破坏准则,即:
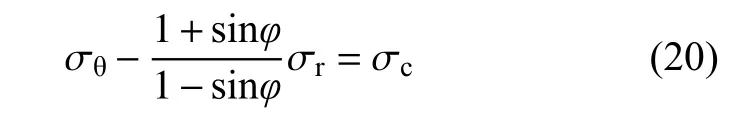
式中:φ为岩石材料的内摩擦角;σc为岩石的单轴抗压强度。
假设围岩内摩擦角φ=20°,单轴抗压强度σc=5 MPa,梯度系数c=0.25 m2,远场应力(即初始地应力)分别取σ0=10、40、70 MPa,此时圆形隧道围岩破裂区位置及宽度如图6 所示。
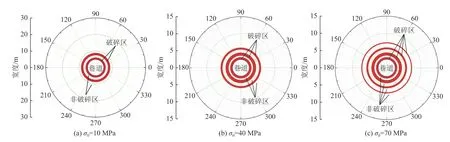
图6 初始地应力σ0 对圆形隧道破裂区的影响Fig.6 Influence of in-situ stress σ0 on the distribution of fractured zones
由图6 可知,随着初始地应力σ0的增大,圆形隧道围岩破碎区数量增加,且破坏范围向外扩展。当初始地应力水平较小时,围岩可能仅出现一个破裂圈,此时围岩将不会发生分区破裂现象。因此,围岩如要出现分区破裂化现象,初始地应力σ0需要达到一定数值,即隧道需要满足一定的埋深要求。
需要特别说明的是,本节关于破碎区的估算并未考虑围岩破坏后的应力重分布,因此,理论预测值和实际测量数据可能存在出入。
5 结 论
a.考虑内部微观结构对宏观力学性质的影响,由提出的梯度模型求得的应力场与变形场以经典弹性解为基准上下波动,表现出显著的准周期性与波动性,为解释围岩分区破裂化现象提供可能。
b.梯度系数对围岩应力场与变形场的影响存在一定规律。梯度系数取值越大,表明材料内部微观结构的尺度越大,此时微观结构对材料宏观力学性能的影响越显著。当梯度系数等于0 时,梯度模型退化为经典弹性理论。
c.通过比较理论计算与试验数据可知,梯度模型可以很好地描述圆形隧道周围的位移场,证明本文所提理论模型的正确性。
d.结合Mohr-Coulomb 破坏准则,估算了圆形隧道围岩破裂区的位置及宽度。研究表明,随着初始地应力σ0的增大,圆形隧道围岩破碎区数量增加,且破坏范围向外扩展。
