穿越沙漠的小游戏策略（二）

张敏 张倩男 邵光祖 孟慧慧 王雪锋

【摘要】本文根据地图1分析玩家走最优路径和其他路径两种情况，列出赢得矩阵，根据对手的策略来选择自己的策略.笔者发现无论对手选择什么样的策略，玩家都会选择最优路径，因此得到两人博弈的支配性策略组合（纳什均衡）：需要在起点购买72箱水、84箱食物.本文根据地图2确定在悲观状态下的天气情况是除沙暴天气以外其余全是高温.三个玩家互相避开在同一时间内挖矿、购买物资和行走相同路径，最终均分三人总的剩余资金.计算得出：一人在挖矿，两人直达终点的情况下，总剩余资金是28175元;在3人轮流挖矿的情况下，总剩余资金是26628元.通过对比，我们发现一人挖矿，两人直达终点的方案最优.根据玩家在最优路线过程中消耗的物资和在行程中购买的物资，我们得知在起点时，玩家A、C均需要购买180箱水、180箱食物.玩家B需要购买137箱水、335箱食物.

【关键词】纳什均衡;悲观准则;乐观准则

玩家凭借一张地图，利用初始资金购买一定数量的水和食物（包括食品和其他日常用品），从起点出发在沙漠中行走.游戏途中会遇到不同的天气，玩家也可以在矿山、村庄补充资金或资源，在游戏设定的规则下和规定的时间内到达终点，并保留尽可能多的资金.

一、问题分析

对于玩家来说，玩家同时从起点出发时会增加玩家“同行”时的消耗，降低玩家“同挖”时的收益，提高玩家“同买”时的价格.

在地图1的情形下，游戏有2名玩家.对于这2名玩家，他们需要提前设定好行动方案.此外，他们在设定行动方案时要尽可能地避免与其他玩家相遇，因此需要猜测对方玩家的心理，这是典型的博弈游戏.由于最短路徑的消耗量是相同的，2名玩家在做决策时要么选择走三天的最优路径，要么选择走其他路径.玩家可以列出玩家们的赢得矩阵（支付矩阵）来分析对方采取的策略，以此得到自己的支配性策略，从而确定一般情况下玩家采取的最优策略组合（纳什均衡）.

在地图2的情形下，游戏有3名玩家，游戏截止时间是第30天.已知一般情况下沙暴天气出现的概率是20%，而本游戏中的30天内较少出现沙暴天气，所以本游戏中出现沙暴天气的概率低于20%.本游戏讨论沙暴天气的概率是3.33%的情况，即沙暴天气在30天内只出现1天的情况.从悲观准则分析，假设30天内有1天沙暴天气，有29天高温天气.从乐观准则分析，假设30天内有1天沙暴天气，有29天晴朗天气.我们分析3名玩家为追求个人的最大利益，均走最优路径的方案是否可取.如果不可取，那么我们讨论3名玩家在合作时互相避开同一时间内挖矿、购买物资和相同路径移动的情况下，轮流挖矿以及一人挖矿、两人直达两种方案的总剩余资金，最终三人均分总剩余资金.

二、模型的建立与求解

（一）地图1情形下模型的建立与求解

根据以往经验，我们知道天气不会对最优路径造成太大影响.我们通过MATLAB软件计算得出：去挖矿的所有路径都不能使玩家到达终点时获得的剩余资金最大，因此，我们选择的路径就是从起点直接到终点，不考虑挖矿.

地图1情形下有2名玩家，记为A和B.假设2名玩家都是理性决策者，他们就会根据对方的策略来确定自己的策略，找出从起点到终点的最短线路.

由于他们都是理性决策者，他们如果选择除最优路径以外的其他路径，那么一定会选择从起点到终点的最近路径.我们把除最优路径以外的路径策略记作else，最优路径的策略记作min.

下面，我们分析玩家A的决策情况.

决策一：当玩家B选择else时，玩家A可以选择else或min.若玩家A选择min，则玩家A胜利;若玩家A选择else，则两人平局.玩家A为了赢得本次博弈会选择min.

决策二：当玩家B选择min时，玩家A仍然可以选择else或min.若玩家A选择min，则两人平局;若玩家A选择else，则玩家A失败.为了赢得本次博弈，玩家A在平局和失败中会选择平局，所以玩家A会选择min.

在这个博弈的过程中，无论玩家B的策略选择如何，玩家A都会选择min.

下面，我们分析玩家B的决策情况.

对于玩家B来说，其面临的博弈局面与玩家A完全相同，所以玩家B也会选择min.博弈双方都使用了支配性策略，他们支配性策略的组合就是纳什均衡.由于事先考虑到对方可能与自己走相同的路径，他们在起点带的食物和水都要满足支撑他们走最大相同路径的消耗.我们最终判定最大相同路径就是（else，else）.

利用MATLAB软件计算，他们需要在起点购买72箱水、84箱食物.

（二）地图2情形下模型的建立与求解

根据当地的天气规律及相应的数据记录，我们计算沙暴天气的概率是630×100%=20%，据此得到沙暴天气在该地区一般情况下的概率.在本游戏中，已知在30天内较少出现沙暴天气，则本游戏中的沙暴天气的概率必然低于20%.本模型讨论的沙暴天气的概率是3.33%的情况，即沙暴天气出现1天的情况.

在本游戏中，如果3名玩家都只追求个人利益的最大化，那么他们都会选择走最优路径.下面给出3名玩家同时走最优路径，其中1名玩家物资消耗的情况，如表1所示.

我们从表1中可以看出，第16天消耗的物资将会超过负重上限1200 kg，即在第16天物资耗尽，游戏失败.当执行策略的玩家面临多次具有淘汰风险的博弈时，他们会以不可逆的趋势向合作的方向发展，因此，他们会选择合作.合作后的三人会将集体获得的总资金进行均分.

设3名玩家分别是A，B，C.

1.轮流挖矿方案

已知30天内出现1天沙暴天气，其余29天均为高温的情况下，一个人挖矿的最大天数是5天.本方案中3人可以走不同路线，即玩家A从起点走最短路径到达矿山，开始挖矿.在玩家B还未到达矿山时，玩家A已挖矿2天.在玩家B到达矿山后，玩家A撤出，玩家B随即开始挖矿，玩家B挖矿5天，这时，玩家A直接走向终点，对玩家B和玩家C的路径、购买物资和挖矿没有产生影响.在玩家C到达矿山后，玩家B撤出，玩家C随即开始挖矿，玩家C挖矿5天，这时，玩家B直接走向终点，对玩家C的路径、购买物资和挖矿没有产生影响.综上所述，该方案的总挖矿最大天数是12天.玩家A，B，C的具体行程如表2所示.

我们按照A的行程利用Excel计算得到A最终的剩余资金是8730元;按照B的行程，利用Excel计算得到B最终的剩余资金是9975元;按照C的行程，利用Excel计算得到C最终的剩余资金是7923元.因此，3人轮流挖矿方案的总剩余资金是26628元.

3名玩家在起点购买（购买物资总量的依据是挖矿最大天数和路程消耗量）和在村庄购买（补充物资总量的依据是挖矿最大天数和路程消耗量）的物质，如表3所示.

由表3可知，玩家A、玩家B和玩家C在起点购买的水分别是432箱、110箱、422箱，食物分别是432箱、670箱、778箱.玩家A不经过村庄，玩家B在村庄没有购买水和食物（即在起点购买的水和食物够用），玩家C在村庄购买745箱水和895箱食物.

2.一人挖矿，两人直达方案

本方案考虑两人从起点直接去终点，即其中2名玩家不经过村庄和矿山.本方案中的玩家A和玩家C从起点直接去终点，对玩家B的路径、购买物资和挖矿没有产生影响.在玩家B到达矿山时，玩家B挖矿5天.综上所述，该方案的总挖矿最大天数是5天.

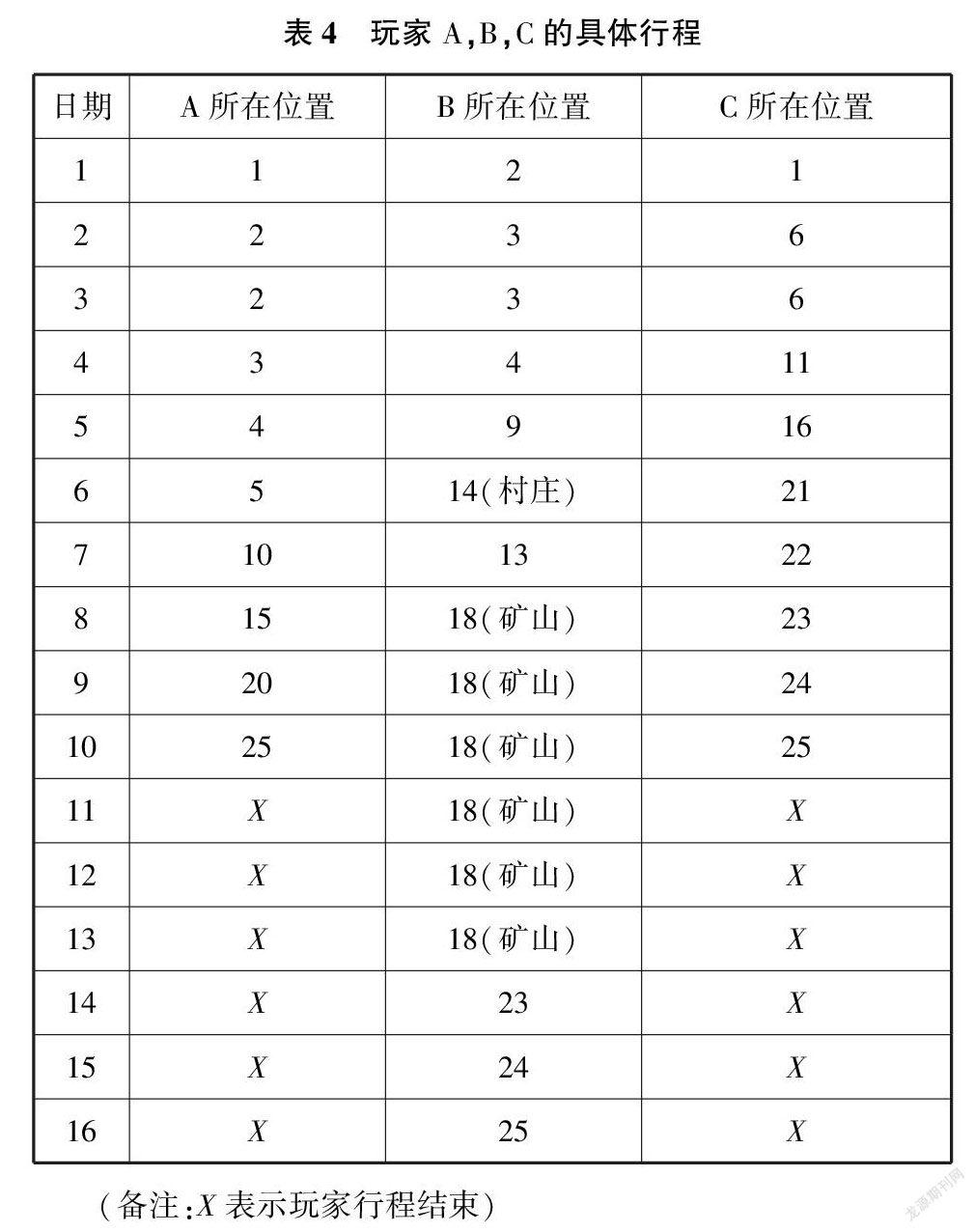
玩家A，B，C的具体行程如表4所示.

这种方案下直达终点的玩家A和玩家C最终的剩余资金均是9100元，玩家B最终的剩余资金是9975元.因此，一人挖矿、两人直达方案的总剩余资金是28175元.

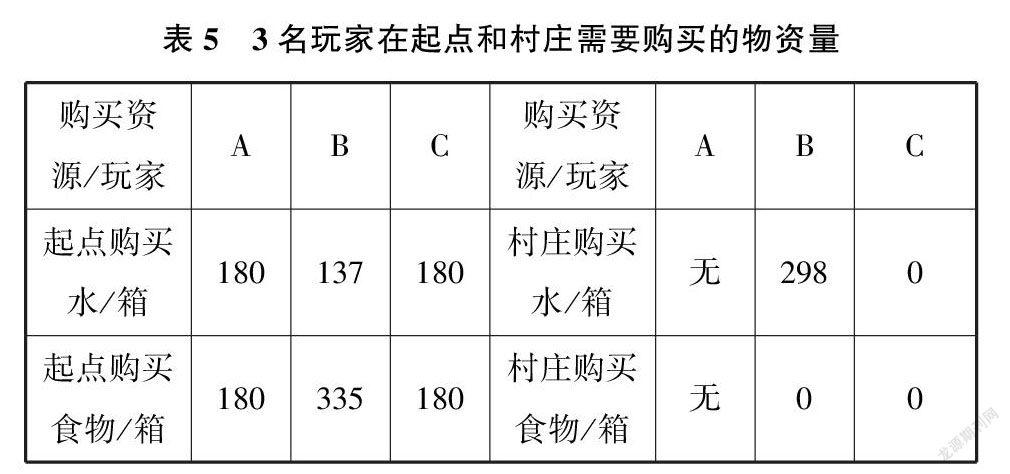
玩家在起点购买（购买物资总量的依据是挖矿最大天数和路程消耗量）和在村庄购买（补充物资总量的依据是挖矿最大天数和路程消耗量）的物资，如表5所示.

由表5可知，玩家A、玩家B和玩家C在起点购买的水分别是180箱、137箱、180箱，食物分别是180箱、335箱、180箱.玩家A不经过村庄，玩家B在村庄购买298箱水，没有购买食物（即在起点购买的食物够用），玩家C在村庄没有购买水和食物（即在起点购买的水和食物够用）.

三、结语

在地图1的情形下，博弈双方都采用支配性策略，玩家A和玩家B的支配性策略都选择min.通过MATLAB软件计算，他们需要在起点购买72箱水、84箱食物.在地图2的情形下，从悲观准则和乐观准则两个角度出发，首先，我们分析了3名玩家均走最优路径方案不可行.其次，我们讨论了3名玩家在合作时互相避开同一时间内挖矿、购买物资和相同路径移动的情况下，轮流挖矿以及一人挖矿、两人直达的两种方案，得出3人轮流挖矿方案的总剩余资金是26628元;一人挖矿、两人直达方案的总剩余资金是28175元.

【参考文献】

[1]严蔚敏， 吴伟民. 数据结构（C语言版）[M].北京： 清华大学出版社，2007.

[2]岳超源.决策理论与方法[M]. 北京：科学出版社，2003.

[3]罗伯特·吉本斯. 博弈论基础[M].高峰，译.北京：中国社会科学出版社，1999.

[4]謝识予. 经济博弈论（第三版）[M].上海：复旦大学出版社，2008.

[5]胡运权. 运筹学基础及应用（第三版）[M].哈尔滨：哈尔滨工业大学出版社，1998.

[6]程理民， 吴江， 张玉林. 运筹学模型与方法教程[M]. 北京：清华大学出版社，2000.

[7]胡运权. 运筹学基础及应用（第四版）[M]. 北京：高等教育出版社，2004.

[8]谷小娜.从“囚徒困境”到多人多次重复博弈的人性假设[J]. 中国集体经济（下半月），2007（11）：31-32.