非均衡市场下房地产寡头产量竞争研究
2015-06-09陈迅赖纯见
陈迅++赖纯见


摘要:在非均衡市场下建立房地产寡头产量竞争动态博弈模型,并分别用理论和数值模拟的方法对其演化加以分析。研究表明,在区域市场非均衡条件下,房地产寡头可以通过重复博弈达成产量竞争均衡;在房地产开发生产技术、管理水平的特定阶段和稳定的税赋政策下,市场供需的非均衡状态和地价房价比决定区域房地产寡头产量博弈的均衡解、均衡稳定性和均衡演化路径,从而决定房地产供给市场的类型。政府宜采取地价房价比控制、市场供需结构调节和税收调整同步的方式调控房地产市场,政策效果相得益彰。
关键词: 非均衡市场;房地产寡头;博弈;纳什均衡;混沌
中图分类号:F224.32文献标识码:A文章编号:1003-7217(2015)03-0099-08
一、引言
区域房地产寡头面临共同的区域需求市场,其产量竞争更接近古诺博弈,是信息不对称、有限理性下的动态行为博弈,且其所处市场环境可能是供需非均衡的。Jing Peng(2011)等研究了具有不变线性成本的延迟有限理性三寡头博弈,发现合适的延迟参数能够扩大系统的稳定区域[1] 。Lu(2011)等研究表明,决策状态延迟能够扩大均衡稳定域并延缓分岔[2]。易余胤(2004)等的研究发现溢出效应能增加博弈达到Nash均衡的可能性[3]。Fabio(2010)研究发现寡头的类型影响均衡的稳定性和其失稳后的复杂动力学演化,但并不影响均衡解本身[4]。Leonard(2009)研究表明,在异质混合双寡头框架下,由于环境税收与减排的影响,私有化将导致社会福利降低[5]。姚洪兴(2005)等研究发现企业加快广告投入量的调整速度,会导致博弈系统的不稳定[6]。Tnu(2006)的研究表明静态古诺博弈均衡解的存在性与参与博弈的寡头数量无关[7]。牟玲玲(2010)等分析了寡头博弈模型演化的复杂性态[8]。童光毅(2008)等针对房地产市场的非均衡状态, 以半参数(拓展)回归模型解释了我国房地产价格持续大幅上涨的原因[9]。阙彬(2011)等在聚合方程下实证分析了房地产市场非均衡状态[10]。姚洪兴(2008)等研究了均衡市场下房地产投资决策博弈模型的复杂性[11]。现有市场模型侧重于宏观方面,缺乏对其区域特性、地区差别和市场主体行为(微观)等因素的考虑;没有反映出均衡与非均衡市场共存的现状及其内在联系。本文拟从区域房产商的产量竞争决策行为及区域市场供求的微观视角,研究区域房地产市场(非)均衡状态、管控政策等与产量分配机制关系的经济规律,期望能为行业运营实践、管控政策制定提供理论参考。
二、模型建立
假设:(1)宏观经济政策、经济形势相对稳定,经济系统运行勿受突变扰动;(2)房地产市场可能呈现非均衡;(3)寡头均以赢利为目的,公益性房产供给不进入市场;(4)寡头是有限理性的,即普遍存在的“短视预期”和“羊群效应”[12]传导所致。我们定义“短视预期”为一期即项目运营平均周期上的有限理性预期,能够根据现有的信息如当期边际利润、价格预期下一期的价格水平,或者至少二者差异的方差很小,可以通过线性的决策系数加以矫正,从而决定下期产量,谓之“一阶理性”;(5)寡头间不存在合谋,产品同质或具有等价替代性,即符合古诺模型的市场结构特点[11,13] 。
从土地使用权买卖行为至房地产产品售罄(或留下一定量的尾盘,不同房地产生产者各异),有一个较长的产销期(如2~5年),但出让土地时,地方政府和房产商均不能确切知道土地未来物化至商品房中的真实价值,一般是根据当期(如t期)对未来建成商品房的预期价格pe(t+1)来决策。根据假设(4),pe(t+1)等于或近似于t+1期实际交易价格p(t+1)①。从土地交易双方关于房地产行业的知识和信息面来看,这也是切合实际的。t期交易的土地价格是t+1期房地产的重要成本,会影响到t+1期房产实际交易价格,进而影响房地产供应量。
若某区域t期房地产市场需求曲线为p(t)=a-bD(t)②,其中a>0,b>0为常系数,a表示区域房地产的最高价格;D(t)>0为t期市场需求。该区域市场上n个寡头生产可代替房地产产品,进行产量竞争。第i个房地产寡头t-1期决策生产t期面市供给量为qi(t),i=1,2,…,n,则t期房地产市场供给S(t)=∑ni=1qi(t)。若区域市场非均衡,第i个寡头t期面临的需求量为qi(t)(1+σi),其中σi≥-1,i=1,2,…,n。σi>0表示超额需求率;-1≤σi<0表示超额供给率,则1+σi反映房地产销售去化率;σi=0时表示供需均衡。因此,该区域t期市场需求D(t)=∑ni=1qi(t)(1+σi),那么,市场需求曲线为:
p(t)=a-b∑ni=1qi(t)(1+σi) (1)
财经理论与实践(双月刊)2015年第3期2015年第3期(总第195期)陈迅.赖纯见:非均衡市场下房地产寡头产量竞争研究
区域t期(t-1期决策的)楼面地价为cpe(t)=cp(t),其中0 πi(t)=(I′i-γ)(a-b∑ni=1qi(t)(1+σi))qi(t)
i=1,2,…,n (2)
令Ii=I′i-γ=1-γ-c1-ri,则Ii为第i个寡头的销售净利率。第i个寡头第t期边际利润函数为:
π′i(t)=πi(t)qi(t)=Ii(a-b∑nj=1qj(t)(1+
σj)-bqi(t)(1+σi))i=1,2,…,n(3)
在非对称需求信息、一阶理性下,多寡头进行动态古诺博弈。寡头们依据其当期产量及边际利润情况来决策下一期产量的调整。第i个寡头t期边际利润π'i(t)>0,则t+1期产量qi(t+1)在qi(t)基础上调整增加,反之则调整降低[14]。
此外,寡头还会根据t期供求状况,对t+1期产量作修正:当t期存在超额供给即-1≤σi<0,则t+1期产量调整σiqi(t);当第t期存在超额需求即σi>0,则超额需求自动积蓄形成下期需求,对t+1期产量不作额外修正。从而,第i个寡头参与古诺重复博弈的产量动态调整机制:
qi(t+1)=qi(t)+αi(qi(t))π'i(t)+Δqi(t)
i=1,2,…,n (4)
其中αi(qi(t))>0,表示第i个寡头产量动态调整速率;Δqi(t)=σiqi(t)σi<00σi≥0,是对t期超额供给的产量修正。假设动态调整速率αi(qi(t))=αiqi(t),i=1,2,…,n。由式(3)和式(4)可以得到多个寡头产量决策重复博弈模型:
qi(t+1)=qi(t)+αiqi(t)Ii(a-
b∑nj=1qj(t)(1+σj)-bqi(t)(1+σi))+Δqi(t)
Δqi(t)=σiqi(t)σi<00σi≥0
Ii=1-γ-c1-rii=1,2,…,n
D(t)=∑ni=1qi(t)(1+σi)
S(t)=∑ni=1qi(t)(5)
三、模型分析
为了简化计算过程,重点讨论双寡头的情形:
q1(t+1)=q1(t)+α1q1(t)I1(a-2bq1(t)
(1+σ1)-bq2(t)(1+σ2))+Δq1(t)
q2(t+1)=q2(t)+α2q2(t)I2(a-2bq2(t)(1+
σ2)-bq1(t)(1+σ1))+Δq2(t)
Δqi(t)=σiqi(t)σi<00σi≥0,i=1,2
Ii=1-γ-c1-ri,i=1,2
D(t)=q1(t)(1+σ1)+q2(t)(1+σ2)
S(t)=q1(t)+q2(t)(6)
对于系统(6)令qi(t+1)=qi(t),i=1,2。(1)若σi≥0,i=1,2,可求得其四个均衡点:E1=0,0,E2=a2b(1+σ1),0,E3=0,a2b(1+σ2),E4=a3b(1+σ1),a3b(1+σ2);(2)若σi<0,i=1,2,系统均衡点:E1=0,0,E2=a+σ1α1I12b(1+σ1),0,E3=0,a+σ2α2I22b(1+σ2),E4=a+2σ1α1I1-σ2α2I23b(1+σ1),a+2σ2α2I2-σ1α1I13b(1+σ2);(3)若σi≥0而σj<0,i≠j,i,j=1,2,如σ1≥0,σ2<0,则系统均衡点:E1=0,0,E2=a2b(1+σ1),0,E3=0,a+σ2α2I22b(1+σ2),E4=a-σ2α2I23b(1+σ1),a+2σ2α2I23b(1+σ2),由对称性,当σ2≥0,σ1<0时,系统(6)有近似均衡点(略);其中Ii=1-γ-c1-ri,i=1,2。下面按以上三种均衡情形,分析博弈系统的特性。博弈系统(6)的Jacobi矩阵为:
J=1+α1I1(a-4bq1(t)(1+σ1)-bq2(t)(1+σ2))+sgn (σ1)σ1-α1I1bq1(t)(1+σ2)-α2I2bq2(t)(1+σ1)1+α2I2(a-4bq2(t)(1+σ2)-bq1(t)(1+σ1))+sgn (σ2)σ2
其中:
Ii=1-γ-c1-ri
sgn (σi)=0σi≥0
1σi<0i=1,2 (7)
命题1当σi≥0,i=1,2时,即在均衡情形(1)下③,区域房地产寡头产量竞争博弈均衡和供给市场类型取决于地方政府土地价格参数c,而与市场供需非均衡程度σi无关;存在Nash均衡解且其稳定性条件与均衡市场下相似[15]。
命题2 当σi<0,i=1,2时,即在均衡情形(2)下④,区域房地产寡头产量竞争博弈均衡和供给市场类型取决于市场的非均衡程度σi和地方政府土地价格参数c的匹配性;产量决策博弈出现零产量、垄断和寡头垄断几种形式的局部稳定均衡;不存在Nash均衡解。
命题3 当σ1≥0,σ2<0时,即在均衡情形(3)下⑤,区域房地产寡头产量竞争博弈均衡和供给市场类型取决于寡头2的市场非均衡程度σ2和地方政府土地价格参数c的匹配性;产量决策博弈出现零产量、垄断(由寡头1)和寡头垄断几种形式的局部稳定均衡;不存在Nash均衡解。
四、数值模拟分析
(一)命题1情形博弈系统分析
1.博弈系统演化。取参数值a=10,b=0.5,c=0.3,α2=0.2,r1=0.5,r2=0.4,σ1=0.1,σ2=0.05,初值q10=3.5,q20=8.6,双寡头博弈系统动态演化过程参见赖纯见、陈迅的研究[15]。图1表明市场均衡并不是房地产寡头博弈Nash均衡的前
图1非均衡市场房地产双寡头产量竞争动态演化(命题1)
参数γ的影响
图2参数调整时双寡头产量竞争动态演化(命题1)
提条件,在市场超额需求下可以形成稳定Nash均衡产量分配。
2.博弈均衡的稳定域。根据命题1,均衡的稳定性仅取决于政府地价参数c(证明详见附录A),取参数值c∈[0.1,0.4],绘出产量博弈寡头垄断和垄断情形Nash均衡解的稳定区域[15]。
3.地价房价比、税收和供求非均衡对博弈的影响。取参数值 a=10,b=0.5,α1=0.5,α2=0.2,r1=0.5,r2=0.4,σ1=0.1,σ2=0.05恒定,地价参数c调整时,双寡头博弈动态演化呈现倒分岔形态过程[16]。图2表明税收γ和地价参数c对博弈系统的影响是相似的,所以,政府采用这两方面的调控政策的效果具有替代性。(二)命题2情形博弈系统分析
1.博弈系统演化。取参数值a=10,b=0.5,c=0.3,α2=0.2,r1=0.5,r2=0.4,σ1=-0.1,σ2=-0.05,初值为q10=3.5,q20=8.6,得到均衡解随α1的变动形态,见图3(a)。这与理论分析的情形(2)均衡解E3寡头2垄断(0<α1≤0.067)、E4寡头垄断均衡(0.067<α1≤1.003)相符,然后通过倍周期分岔进入混沌区域(α1>1.003)。图3(b)反映寡头产量博弈均衡是在市场非均衡下达成的。由图3看到,在同一地价参数c=0.3下,系统可以呈现垄断均衡或寡头垄断均衡,这与命题1的情况是完全不同的。政府已经不能单靠地价房价比的控制来实现市场类型管控和调节。
2.博弈均衡的稳定域。根据均衡稳定性条件④,固定参数a=10,b=0.5, r1=0.5,r2=0.4,σ1=-0.1,σ2=-0.05,初值为q10=3.5,q20=8.6,变动c、α1、α2可用数值分析更直观地描述,见图4。
(a)均衡状态 (b)市场需求和供给演化
图3非均衡市场双寡头产量竞争博弈演化(命题2)
(a)c∈[0.1,0.3] (b)c=0.1
图4不同地价参数下非均衡市场双寡头产量竞争均衡的稳定区域(命题2)
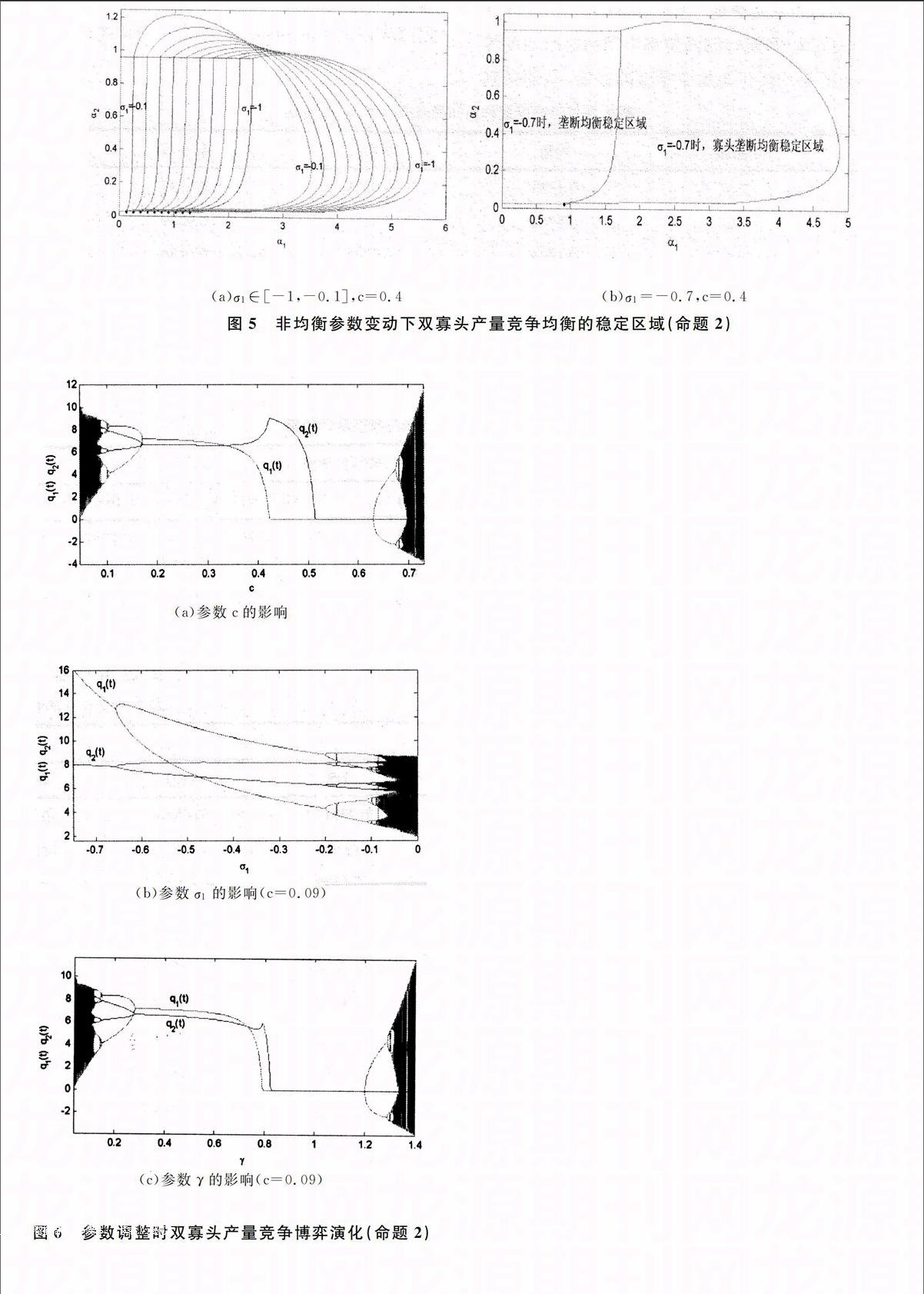
图4(a)是不同的地价参数c下的均衡稳定域,随地价参数c递增而扩大;但当c≥0.4时,稳定的均衡类型是垄断还是寡头垄断还要取决于市场非均衡参数σ1,σ2。取c=0.4,间隔0.1变动市场参数σ1绘制博弈均衡稳定域,见图5(a)、(b)。
3.地价房价比、税收和供求非均衡对博弈的影响。取参数α1=0.5、α2=0.2不变,只调节参数c、σi、γ的情形,见图6。图6表明参数c、σi、γ均能在不同程度上改变系统的混沌态,而图6(a)和(c)演化过程近似,表明土地价格和税负管理政策效果具有替代性。
(a)σ1∈[-1,-0.1],c=0.4 (b)σ1=-0.7,c=0.4
图5非均衡参数变动下双寡头产量竞争均衡的稳定区域(命题2)
(a)参数c的影响
(b)参数σ1的影响(c=0.09)
(c)参数γ的影响(c=0.09)
图6参数调整时双寡头产量竞争博弈演化(命题2)
(三)命题3情形博弈系统分析
1.博弈系统演化。取a=10,b=0.5,c=0.3,α2=0.2,r1=0.5,r2=0.4,σ1=0.1,σ2=-0.05,初值为q10=3.5,q20=8.6,得到寡头垄断稳定均衡解随α1调整的演化形态,见图7(a);其他参数不变,若取α1=0.5,可得该系统均衡随α2调整的演化形态,大致经历以下过程:垄断(由寡头1)E2(0<α2≤0.026)、寡头垄断E4(0.026<α2≤0.669),然后通过倍周期分岔进入混沌区域(α2>0.669),见图7(b)。寡头2在全局最优选择下作依赖于市场状况的存量调整,从而该均衡结果是次优的,不存在Nash均衡。图7(c)、(d)表明,在总需求大于总供给下,房地产寡头博弈也可以达成稳定均衡。
2.博弈均衡的稳定域。根据稳定性条件⑤,固定参数a=10,b=0.5, r1=0.5,r2=0.4,σ1=0.1,σ2=-0.05,初值为q10=3.5,q20=8.6,变动c、α1、α2绘制出垄断(由寡头1)均衡E2和寡头垄断均衡点E4的稳定性域,见图8(a)、(b)。
调整市场非均衡参数σ1、σ2绘制出系统的均衡稳定域,见图9。图9(a)表明,超额需求σ1变动不会改变系统均衡稳定区域;而图9(b)则反映出超额供给参数σ2的变动会改变系统的均衡稳定性,而且这种影响并不独立于地价参数c,如图9(b)和图8(a)形态近似,但稳定域空间随市场波动较大。所以,同步采取限制地价房价比和调整税负水平政策的同时,还应加强市场供需结构的管理,避免各项调控政策的施行效果将呈跷跷板现象。
3.地价房价比、税收和供求非均衡对博弈的影响。取σ1=0.1、σ2=-0.05、α1=0.5、α2=0.2,其他参数不变,调整地价参数c,发现系统呈现与命题2下类似的演化过程,见图10(a)。市场非均衡因素σ2的变动并不能使系统在均衡状态和混沌状态间转换,见图10(b)。
图10(c)与图10(a)演化形态类似,说明房地产业承担的综合税负与地价参数c对房地产系统的影响是近似的。
(a)迭代均衡( 0<α1<1.44) (b)迭代均衡(0<α2<1.06)
(c)市场需求和供给演化(0<α1<1.44) (d)市场需求和供给演化(0<α2<1.06)
图7非均衡市场双寡头产量竞争博弈演化(命题3)
(a) E2、E4,c∈[0.1,0.4] (b)E2、E4,c=0.1
图8地价参数变动下非均衡市场双寡头产量竞争均衡的稳定区域(命题3)
(a)E2、E4,c=0.3,σ1∈(0,1) (b) c=0.3,σ2∈[-1,-0.1]
图9非均衡参数变动下双寡头产量竞争均衡的稳定区域(命题3)
(a)参数c的影响
(b) 参数σ2的影响(c=0.08)
(c)参数γ的影响(c=0.3)
图10参数调整时双寡头产量竞争博弈演化(命题3)
五、结语
本文建立的模型是对经典的静态完美Cournot模型进行特定的动力学改良,更符合房地产行业产量分配动态演化的实际情况。以二寡头产量竞争为例,研究区域房地产非均衡市场下动态博弈混沌态、垄断均衡、寡头垄断均衡、滞涨均衡的均衡解及其渐进稳定区域特性。研究结果论与建议:(1)房地产寡头产量竞争博弈可达成均衡,但市场的非均衡性会影响产量竞争博弈Nash均衡的存在性及稳定性;该博弈在市场均衡下的情形仅是其在非均衡市场下的一个特例;(2)区域房地产供给市场类型主要取决于市场供需非均衡程度、行业税负率和地方政府对土地价格管理,政府的行业管控措施适宜从这三方面着手;(3)地价房价比控制、税负水平管理两方面调控政策具有替代性,但均受制于市场供需结构关系。同步采用供需结构管理、地价房价比控制和税负管理的组合调控政策,效果更佳,且能够有效杜绝调控政策实施中的跷跷板效应;(4)房地产市场宏观管控政策不宜通过直接作用于供给量或需求量以实现全民普惠,谨防市场在全面超额需求和全面超额供给间来回转换,如限购等直接行政干预手段可能将市场引向更加难以掌控的反向局面。
注释:
①理论上的综合平均价格,忽略房地产类别、方位和销售时间先后等因素形成的复杂的、持续变化的销售价格差异。
② 将需求函数改变成形式为p(t)=a-bD(t)-b1D(t)2…-bn-1D(t)n的多项式,模型相关研究结论与本文一致,为简化计算,本文仅研究线性需求函数的情形。
③篇幅所限,证明过程参见文献[16],其结论完全一致,即当寡头普遍存在超额需求时,区域房地产产量竞争均衡稳定性和供给市场类型取决于地方政府地价管控参数c,而与市场供需非均衡程度σi无关,原因在于商品房供给时滞效应和运营成本中土地成本的占比差异。这也表明市场均衡条件下的该产量竞争博弈均衡仅是非均衡市场下情形的一个特例。
④证明:(1)E1处的Jacobi矩阵为JE1=1+aα1I1+σ1001+aα2I2+σ2。它的两个特征值λi=1+aαiIi+σi,其中a>0,αi>0,-1≤σi<0, i=1,2。E1的稳定条件λi<1,解不等式可以得出-2-aαiIi<σi<0且-2aαi
(3)由对称性,可以相应得出E3的稳定条件。
(4)E4的Jacobi矩阵为JE4=1-23aα1I1-43σ1+2α1I13α2I2σ2-1+σ23(1+σ1)(aα1I1+2σ1-α1I1α2I2σ2)-1+σ13(1+σ2)(aα2I2+2σ2-α2I2α1I1σ1)1-23aα2I2-43σ2+2α2I23α1I1σ1,其特征多项式D(λ)=D0+D1λ+D2λ2, 其中D2=1,D1=-2+23aα1I1+23aα2I2+43σ1-2α2I23α1I1σ1-2α1I13α2I2σ2+43σ2,D0=1-23αα1I1-23αα2I2+13α2α1I1α2I2-43σ1+13αα2I2σ1+2α2I23α1I1σ1-2α2I23α1I1σ21-43σ2+13αα1I1σ2+2α1I13α2I2σ2+53σ1σ2-2α2I12α1I2σ22。根据Jury离散系统稳定性的充要条件,均衡点E4稳定性条件为D(1)=D0+D1+D2>0
D(-1)=D0-D1+D2>0
|D0| ⑤证明:(1)E1的稳定条件-2aα1
D(-1)=D0-D1+D2>0
|D0| 参考文献: [1]Jing Peng,Zehua Miao,Fang Peng.Study on a 3-dimensional game model with delayed bounded rationality[J].Applied Mathematics and Computation, 2011,218(5):1568-1576. [2]Lu Yali.Dynamics of a delayed duopoly game with increasing marginal costs and bounded rationality strategy[J].Procedia Engineering,2011,15(4):4392-4396. [3]易余胤,盛昭瀚,肖条军.具有溢出效应的有限理性双寡头博弈的动态演化[J].系统工程学报,2004,19(3):244-250. [4]Fabio Tramontana. Heterogeneous duopoly with isoelastic demand function[J].Economic Modelling, 2010,27(1):350-357. [5]Leonard F.S.Wang,Jean Wang.Environmental taxes in a differentiated mixed duopoly[J].Economic Systems,2009,33(4):389-396. [6]姚洪兴,徐峰.双寡头有限理性广告博弈模型的复杂性分析[J].系统工程理论与实践,2005,25(12):32-37. [7]Tnu Puu. On the stability of cournot equilibrium when the number of competitors increases[J]. Economic Behavior & Organization,2006,16(3-4):1606-1618. [8]牟玲玲,陈立文,张俊玲. 非均衡房地产市场博弈行为复杂性研究[J].系统工程学报,2010,25(6):824-828. [9]童光毅,刘星.我国房地产价格的非均衡性[J].管理世界,2008,(1):175-177. [10]阙彬.房地产市场供求非均衡[M].成都:西南交通大学出版社,2011. [11]姚洪兴,王国栋.一类房地产投资模型的复杂性分析[J].统计与决策,2008,253(1):56-57. [12]陈林,朱卫平.基于二手市场与理性预期的房地产市场机制研究[J].管理科学学报,2011,14(2):61-70. [13]侯文宇.古诺线性模型与中国房地产[J].首都师范大学学报(自然科学版),2008,29(5):1-6 [14]马军海,彭靖. 延迟决策对一类寡头博弈模型的影响分析[J].系统工程学报,2010,25(6):812-817. [15]赖纯见,陈迅.房地产寡头有限理性博弈模型的复杂性分析[J].系统工程学报,2013,28(3):285-296. (责任编辑:漆玲琼)
