磁无序及合金化效应影响Co2CrZ (Z=Ga,Si,Ge)合金相稳定性和弹性常数的第一性原理研究*

2022-06-04杨顺杰李春梅周金萍

物理学报 2022年10期

杨顺杰李春梅周金萍

(沈阳师范大学物理科学与技术学院,沈阳 110034)

采用确切的Muffin-Tin 轨道结合相干势近似方法,本文系统计算研究了0 K 下,磁无序及合金化效应影响Co2CrZ (Z=Ga,Si,Ge)合金L21 和D022 相稳定性的规律性及物理机理.研究结果表明,0 K 下,L21 相合金晶格常数、体弹性模量、磁矩和弹性常数均与理论和实验值基本吻合;铁磁下合金具有L21 结构,随磁无序度(y)的增大,L21 相能量相对逐渐增大,最终由低于转变到高于D022 相,因此,当y ≥ 0.1(0.2)时,Z=Si 和Ge(Z=Ga)的合金具有D022 相稳定结构;随y 的增大,L21 相的四方剪切弹性模量(C′=(C11—C12)/2)还不断软化,表明无论在能量还是力学角度上,磁无序都有利于3 种合金发生四方晶格变形;磁无序影响L21 和D022相相对稳定性的电子结构机理归因于Jahn-Teller 不稳定性效应;对于L21 相Co2CrGa1—xSix 和Co2CrGa1—xGex四元铁磁合金,随x 的增大,总磁矩均按照Slater-Pauling 定律单调增大,C′同时也都变硬,表明Si 和Ge 掺杂均有利于增强Co2CrGa 合金L21 相的力学稳定性,从而抑制了其四方晶格变形的发生.

1 引言

1903 年,德国化学家Frite Heusler[1]发现由非铁磁性元素组成的Cu2MnAl 和Cu2MnSn 合金具有强铁磁性,并由此将该类合金命名为Heusler合金.100 多年来,科学家们陆续发现了更多的X2YZ 型Heusler 合金,其中X 和Y 为过渡金属元素,Z 为主族元素,代表性的有X 为Co[2],Mn[3],Pd[4],Ni[5],Cu,Fe[6]等.它们绝大多数在立方相下具有L21结构,也有小部分合金具有XA 或B2结构.实验研究发现,Heusler 合金可具有半金属性[7]、超弹性[8]、形状记忆效应[9]等丰富的物理性质,广泛地应用于自旋电子学[10]、可调带隙半导体[11]、热电材料、磁致伸缩和磁形状记忆合金等领域.对于Co2-[2],Ni2-[5]和Fe2-[6]基Heusler 型磁形状记忆合金,它们还具有磁致冷[12]、巨磁致和巨磁阻效应[13].作为一种重要的磁性功能材料,它们已经在医疗卫生、电子信息和航空航天系统等方面广泛应用,与日常生活密切相关.

Co2-基Heusler 合金因普遍具有较高的自旋极化率和居里温度而备受关注.此外,类似于Ni2MnGa合金,部分Co2-基Heusler 合金如Co2NbSn[14]和Co-Ni-Ga[15],也能发生由立方L21到四方D022相的可逆马氏体相变(martensitic transformation,MT),展现形状记忆效应,有望成为良好的磁形状记忆合金候选材料.最近几年,Xu 等还实验证实了Co-V-Ga,Co-V-Ga-Si[16],Co-Cr-Al-Si[17]和Co-Cr-Ga-Si[18]等非化学计量比Co2-基Heusler 合金同样具有MT 行为.随温度的降低,这些合金均会发生磁转变,由顺磁(PM)转变到铁磁(FM)状态.其中,CoxCr78—xGa11Si11合金体系还能够发生一系列奇特的结构相变[19]:PM L21-PM D022-FM D022-FM L21,从而在单一冷却的过程中,实现了L21-D022-L21连续马氏体相变,即具有冷却诱导的形状记忆效应.其中,L21-D022相变为正常MT,而D022-L21相变则被称为再入马氏体相变(reentrant martensitic transformation,RMT).进一步,通过热磁化测量发现[19],CoxCr78—xGa11Si11合金在PM状态下,L21-D022正常MT 临界温度(TM)可高达620—740 K,而在FM 状态下,D022-L21的RMT对应的TM值低至150 K 左右.该合金体系TM对成分的变化范围大,且在FM 和PM 状态下具有截然相反的TM-x单调变化趋势,更有望应用于复杂的温度控制系统.然而,在CoxCr79—xAl10.5Si10.5合金体系[20],仅当组分x＞ 55.8时,在室温附近能观测到磁场诱导的L21-D022正常MT,且TM随x的增大而升高.可见,不同的合金化成分和磁有序构型均对Co2CrZ基合金L21和D022相的相对稳定性具有重要影响.

理论计算发现,X2YZ 型Heusler 合金MT 多源于其母相四方剪切弹性常数(C ′=(C11—C12)/2)的软化,并与合金奥氏体和马氏体相间的能量差(ΔEAM)、合金原子的价电子数(e/a)有关.如,在Ni-Mn-Ga 合金中[21,22],TM实验值通常随C′的减小而升高;在Ni2FeGa1—xZnx合金中[23],随着Zn含量的不断增大,ΔEAM增大,TM升高;在CoxCr79—xAl10.5Si10.5合金中[20],TM还随着e/a的增大而升高.此外,类似于Ni-Mn-Ga 合金,部分非化学计量比Co2-基Heusler 合金L21与D022间的相变,近年来也被归功于费米面附近自旋向下的电子态密度,即Jahn-Teller 不稳定性效应[24].然而,关于Co2CrZ(Z=Ga,Si,Ge)合金L21和D022相的相对稳定性电子结构机理、及其与弹性常数和两相能量差异间的关联,目前还鲜有文献报道.因此,系统研究驱动它们发生MT 和RMT 的物理机理具有重要意义.

本文采用第一性原理精确Muffin-Tin 轨道(exact muffin-tin orbitals,EMTO)结合相干势近似(coherent potential approximation,CPA)方法[25,26],系统计算确定了L21-Co2CrZ(Z=Ga,Si,Ge)合金的基态性质,给出了四方晶格变形及磁无序影响它们电子总能、磁矩、弹性常数和电子结构的规律性,探讨了磁无序制约其L21和D022相相对稳定性的物理机理.进一步,以Co2CrGa1—xSix和Co2CrGa1—xGex四元合金体系为例,计算了合金化成分对它们基态性质、磁矩和弹性常数的影响规律,并分析了这些成分依赖性规律与其L21和D022相相对稳定性间的关联.为实验上Co2CrZ基磁形状记忆合金性能的优化设计提供了理论参考.

2 结构与计算方法

Co2CrZ(Z=Ga,Si,Ge) 合金立方相具有L21结构,如图1(a)所示,原子占位情况分别为:Co(0.25,0.25,0.25)和(0.75,0.75,0.75),Cr (0.5,0.5,0.5),Z(0,0,0).L21结构具有面心立方对称性,空间群为.当发生四方马氏体相变时,Co2CrZ合金将沿着母相(1,1,0)方向发生四方剪切晶格变形,形成D022结构,如图1(b)所示,其具有体心四方对称性,空间群为I4/mmm.随着温度的升高,Co2CrZ合金还会发生由FM 到PM 的磁相变.根据部分原子磁无序模型[27],它们可以表示为赝二元合金:(Co2CrZ)↑y(Co2CrZ)↓1—y,y=0表明合金处于FM 状态,y=0.5 则意味着其处于PM 状态.

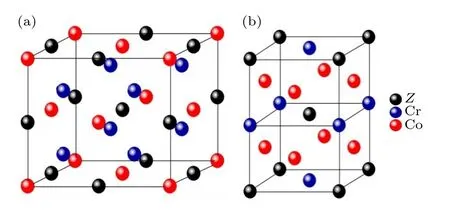
图1 Co2CrZ (Z=Ga,Si,Ge)合金晶格结构:(a) L21相;(b) D022 相Fig.1.Crystal structures of Co2CrZ (Z=Ga,Si,Ge) alloys:(a) L21 phase;(b) D022 phase.

第一性原理EMTO 方法采用格林函数技巧去求解单电子Kohn-Sham 方程,单电子势用最优重叠的muffin-tin 势函数近似,总能用全电荷密度方法来求解.EMTO 方便与CPA 方法相结合,而后者可有效地处理金属间化合物中的原子和磁无序问题.因此,EMTO-CPA 方法已被广泛应用于Ni-Mn-Ga[24],In-Ti[28],Fe-Pd[29]和Co-V-Ga[30]等无序合金的基态性质和弹性常数的计算.在本文中,EMTO 波函数基组选取s,p,d 和f 轨道,采用标量相对论近似和软核近似;格林函数的计算选取了半圆轮廓上呈指数分布的32 个复数能量点;电子交换-关联势采用由Perdew-Burke-Ernzerhof(PBE)[31]描述的广义梯度近似(generalized gradient approximations,GGA)方法;布里渊区采用17 ×17×17 的均匀k点网格;原子价电子组态为Co-3d74s2,Cr-3d54s1,Ga-4s2p1,Ge-4s2p2和Si-3s2p2.

平衡态下,L21相晶格参数(a)、体弹性模量(B)和磁矩均由Morese 函数对9 个电子总能(E)-体积(V)数据点进行拟合得到.立方晶格具有3 个独立的弹性常数C11,C12和C44.剪切弹性常数C44和C′由体积守恒变形下的电子总能对二阶应变的变化关系求导给出.这里分别采用如下体积守恒的正交和单斜变形:

对应的能量随应变的变化关系为

C11和C12可以根据B=(C11+2C12)/3 和C′=(C11−C12)/2 计算得出.这里,应变量δ选取6 个值,分别为0,0.01,0.02,0.03,0.04 和0.05;采用Hill 平均值法求解多晶剪切模量(G)和杨氏模量(E),具体表达式参见文献[32],式中剪切模量(GV和GR)分别由Voigt 和Reuss 近似法确定[32].

3 结果与讨论

3.1 L21 相平衡态下的基本性质

表1 给出了L21-Co2CrZ(Z=Ga,Si,Ge)合金在FM 和PM 两种不同状态下,a和B的EMTO计算结果与其他理论和实验值的对比.在FM 状态下,3 种合金L21相的a和B值大小都能够与表中其他理论结果较好地吻合[12,33,34,36,38];与已有的实验值相比[35,37],它们a值的误差分别不超过0.42%和0.02%,均在第一性原理计算误差范围内,该结果确保了本文EMTO 方法计算Co2CrZ合金基态性质的精确性.比较发现,Z=Si 合金的a值最小,而其他两种合金的a值相差不超过0.02 Å(1 Å=0.1 nm),该结果可能归功于Si 原子的共价半径(1.11 Å)相对较小,而Ga(1.26 Å)和Ge(1.22 Å)原子的对应值大小基本相当.值得注意的是,当磁有序由FM 转变到PM 状态时,每一种合金的a值均略微变大,而B值变小,表明磁无序不利于3 种合金中原子的紧密排布,并降低了它们体系的体弹性模量.

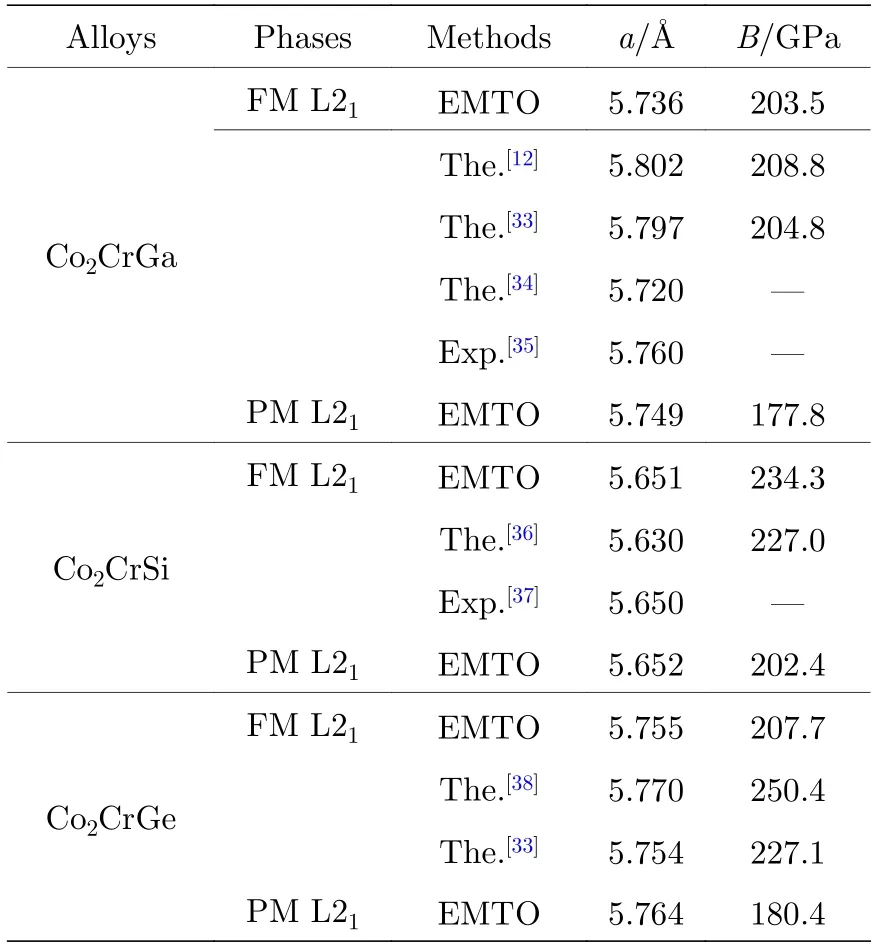
表1 铁磁(FM)和顺磁(PM)状态下L21-Co2 CrZ (Z=Ga,Si,Ge)合金晶格常数和体弹性模量的EMTO 计算结果与其他源于文献[12,33-38]理论和实验值的对比Table 1.Lattice constant and bulk modulus of the FM and PM L21-Co2CrZ (Z=Ga,Si,Ge) alloys calculated with the EMTO program are in comparison with the other theoretical and experimental data from Refs.[12,33-38].

如图2 所示,对于FM 状态下Co2CrGa1—xSix和Co2CrGa1—xGex四元合金体系,随着x从0 增至1,L21相的a和B值均呈单调变化趋势:前者a减小,B增大;后者a和B均略显增大的趋势.在图2(a)中,对于Si 掺杂的四元合金体系,EMTO-CPA 计算给出的a—x变化关系与实验测量结果[18]基本一致.对于Co2CrGa1-xGex四元合金,Seema 等[33]利用赝势超晶胞方法计算给出a随x的增大略微单调降低.事实上,对比表1,从图2(a)更能清晰地看出,由于Ga 和Ge 原子共价半径相差不多,a对x从0 增至1 时的变化量甚至小于对应x=0 时,不同计算给出的a值的差异,导致Co2CrGa 和Co2CrGe 合金的a值大小关系并非十分清晰,其依赖于第一性原理计算方法的不同而不同.在图2(b)中,针对Co2CrGa1-xGex四元合金体系,EMTO-CPA 和赝势超晶胞方法[33]都能够计算给出B随x的增大近乎缓慢增大的趋势.因此,这里将本文与文献[33]计算给出的该四元合金体系a对x的略微变化关系不同,归因于二者方法的不同所致.

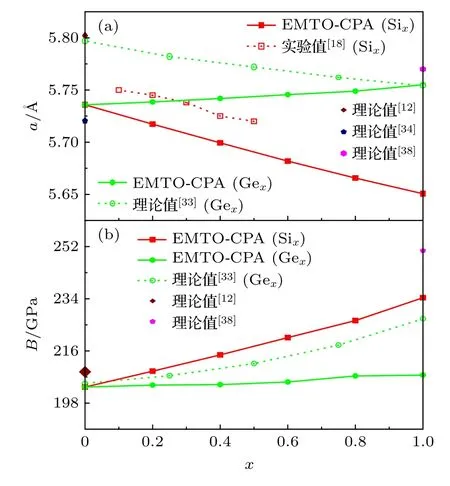
图2 铁磁状态下L21-Co2CrGa1—xSix 和L21-Co2CrGa1—xGex(0 ≤ x ≤ 1)合金晶格常数和体弹性模量随x 的变化关系与文献[12,18,33,34,38]的理论和实验结果的对比 (a) a;(b) BFig.2.x-dependence of the lattice constant and bulk modulus of the FM L21-Co2CrGa1—xSix and L21-Co2CrGa1—xGex (0 ≤x ≤ 1) alloys are in comparison with the available theoretical and experimental data from Refs.[12,18,33,34,38]:(a) a;(b) B.

3.2 马氏体相变

图3 给出了Co2CrZ(Z=Ga,Si,Ge)合金相对电子总能(ΔE)随四方晶格变形(c/a)的变化关系.这里,在任意y下,每一c/a值对应的ΔE值均等于该结构的电子总能减去合金FM 状态L21结构(即y=0,c/a=1)的电子总能.当y=0 时,即在FM 状态下,3 种合金的ΔE均具有两个局域极小值,一个在c/a=1 处,对应L21相;一个在1.2—1.3 附近,对应D022相,且其ΔE值均为正数,分别约为2.03 mRy,2.68 mRy 和2.27 mRy.因此,0 K 下,D022相比L21相的电子总能更高,各合金在FM 状态下具有L21稳定结构.

随着y从0 增至0.5,各合金由FM 逐渐转变到PM 状态,L21和D022相的ΔE值均相应地逐渐增大;相比D022相,L21相下ΔE增大的速度更大,表明磁无序的增大,有助于降低D022相对L21相的能量,从而促进了D022相的相对稳定性.类似于y=0,当y≠0 时,两相相比,ΔE值越低,对应的结构同样则越稳定;反之,则越不稳定.对于Co2CrGa 合金(图3(a)),当y增至0.2 时,D022相变得比L21相能量更低,约低0.21 mRy;随着y继续增大,相比L21相,D022相的ΔE值相对越来越更低.可见,当y≥ 0.2 时,电子总能有利于Co2CrGa 合金具有D022稳定结构,且随y的增大,D022相的稳定性相对L21相越来越更强.对于Co2CrSi(图3(b))和Co2CrGe 合金(图3(c)),当y增至0.1 时,D022相就开始变得比L21相能量更低,分别低约0.49 mRy 和0.41 mRy.因此,当y≥0.1 时,两种合金D022结构也变得更加稳定,且随y的增大,该相的相对稳定性越来越强.

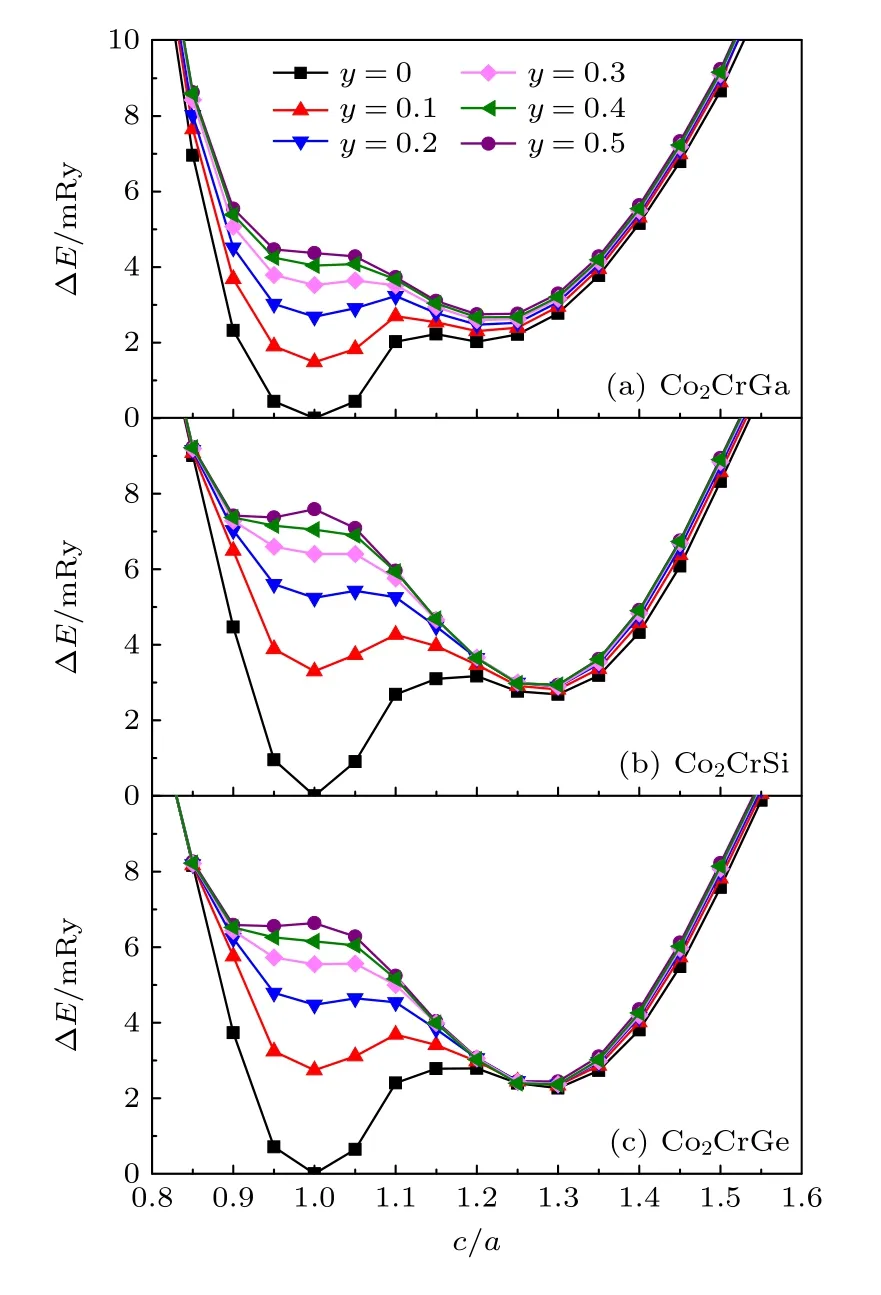
图3 Co2CrZ(Z=Ga,Si,Ge)合金ΔE 随四方晶格c/a 的变化关系,本文ΔE 的计算以各合金FM 状态下L21 相(即y=0,c/a=1)的电子总能作为参考值 (a) Z=Ga;(b) Z=Si;(c) Z=GeFig.3.ΔE of Co2CrZ(Z=Ga,Si,Ge) alloys change with respect to the c/a of tetragonal lattice,here,the electronic energy of the FM L21 structure (y=0,c/a=1) is as reference for ΔE calculations of each alloy:(a) Z=Ga;(b) Z=Si;(c) Z=Ge.

在不考虑能量其他温度依赖性因素的情况下,从图3 得出结论,3 种Co2CrZ合金PM 下,由于D022相能量更低,它们可发生L21-D022的正常MT;当它们由PM 转变到FM 状态的过程中,磁有序化则最终会导致L21相的电子总能低于D022相,从而有助于D022-L21的RMT 行为的发生.目前,实验上测得,CoxCr78—xGa11Si11四元合金体系RMT 对应的TM值处于150—350 K 之间[19],即处于室温附近及以下.然而,除此之外,关于其他Co2CrZ基三元、四元合金RMT 相变行为还少有实验报道.通过考虑能量的成分和温度双重依赖性[39],可以计算并比较L21和D022相的自由能随成分及温度的双重变化规律,从而预测出合金马氏体相变的临界成分及相应的TM值.此项工作也是我们接下来正进行的研究内容.

3.3 磁矩

在FM 状态下,L21-Co2CrZ(Z=Ga,Si,Ge)合金的总磁矩(µtot)分别为:3.02µB,4.01µB和4.01µB,与实验测量值(3.01µB[40],4.00µB[24]和3.99µB[12])非常吻合.如图4(a)所示,在四方变形下,当c/a<1 时,各合金µtot随c/a的增大而增大;当c/a＞ 1 时,µtot则随c/a的增大而减小.可见,3 种合金均在L21相下具有相对最大的µtot值,而D022相的µtot值均比L21相小很多,近乎达小2µB左右.进一步,通过对比Co,Cr 和Z原子的局域磁矩(µCo,µCr和µZ)还发现,各合金总磁矩主要源于µCo和µCr的贡献(图4(b)和4(c)),且它们对c/a的变化趋势与µtot—c/a基本相同.µZ非常小,接近于0,说明Z原子近乎是非自旋极化的.

在PM 状态下,3 种合金的µtot均为0.Co 和Z原子一样,也变为几乎非自旋极化,只有Cr 原子具有局域磁矩,其绝对值大小随c/a的变化如图4(d)所示.可见,随Z从Ga 变化到Ge、再到Si,L21相µCr绝对值大小逐渐增大.同样地,PM 合金µcr绝对值大小也倾向于随体系四方晶格变形量|1—c/a|的增大而减小,即L21相µCr绝对值相对最大.相比D022相,其近乎大0.5µB左右.

随温度的升高,Co2CrZ合金由FM 转变到PM 状态,即体系y从0 增至0.5.图3 证明在此过程中,L21和D022相相对电子总能ΔE均发生常规变化,即单调升高,然而,相比L21相,D022相ΔE值随y增大而增大的趋势并非十分明显,尤其是Z=Si 和Ge 的合金.对比图4(a),可将其归因于L21相具有相对D022相巨大的µtot,大2µB左右.µtot越大,合金磁激发能(即FM 和PM 状态电子总能差异)通常会越高.相应在图3中,随y从0 增至0.5,L21相ΔE升高得就会更快些,并最终由低于转变到高于D022相的对应值,从而导致D022相比L21相更稳定.

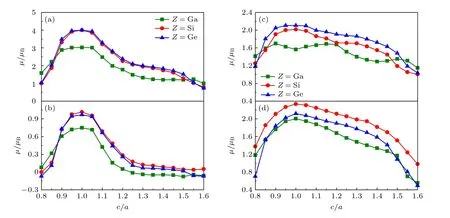
图4 FM 状态下Co2CrZ(Z=Ga,Si,Ge)合金总磁矩(µtot)及Co(µCo),Cr(µCr)原子局域磁矩随四方晶格c/a 的变化关系、及其顺磁PM 状态下µCr 绝对值大小随c/a 的变化关系 (a) FM-µtot;(b) FM-µCo;(c) FM-µCr;(d) PM-µCrFig.4.µtot and µCo and µCr atoms of the FM Co2CrZ(Z=Ga,Si,Ge) alloys change with respect to c/a,together with the trends ofµCr-x of the three PM alloys in their absolute values:(a) FM-µtot;(b) FM-µCo;(c) FM-µCr;(d) PM-µCr.

图5 给出了FM 状态下L21-Co2CrGa1—xSix和Co2CrGa1—xGex合金磁矩随组分x的变化关系.可见,随着x的增大,µCo和µCr单调增大,µtot因而也逐渐增大.通常,根据Slater-Pauling (S-P)定律[41],FM 状态下L21相Heusler 合金的µtot值可用公式µtot=M-24 来描述,其中M为合金原子总价电子数.显然,如图5 所示,本文EMTO-CPA结果与S-P 定律计算给出的µtot-x关系十分吻合.在任意x值下,由于Si 和Ge 原子的价电子数都是4,两种合金的M值相同,它们的µtot,µCo和µCr值也基本类似,表明其确实与合金价电子数有重要关联.

图5 FM 状态下L21-Co2CrGa1—xSix 和L21-Co2CrGa1—xGex(0 ≤ x ≤ 1)合金µtot 与µCo,µCr 原子磁矩随x 的变化关系、及其与Slater-Pauling(S-P)定律计算给出µtot-x 关系的对比Fig.5.µtot and µCo,µCr atoms of the FM L21-Co2CrGa1—xSix and L21-Co2CrGa1—xGex (0 ≤ x ≤ 1) alloys change with respect to x,in comparison with their calculated trends ofµtot-x according to the Slater-Pauling (S-P) rule.

3.4 弹性常数

如表2 所示,Co2CrZ(Z=Ga,Si,Ge)合金FM 状态下L21相的单晶弹性常数C11,C12,C44,C′,弹性各向异性(A=C44/C ′)及G和E的EMTO计算结果均接近于其他理论值[36,42].该结果再次证明了本文所采用的EMTO 软件及其相关参数计算Co2CrZ合金的精确性.

立方晶系的稳定性要求为:C11＞ |C12|,C11+2C12＞ 0 和C44＞ 0[32].显然,表2 给出的3 种合金0 K 下的弹性常数均满足该力学稳定性要求.其中,四方剪切弹性常数C′和A对描述立方相的稳定性还具有更重要的意义.通常情况下,C′越小、而A越大,对应体系则越容易发生L21-D022的MT.如图6 所示,随y的增大,3 种合金C ′和C44均减小,而A逐渐增大,表明C ′减小的速度更快,因而对体系的稳定性随y的变化具有更重要的贡献.随y从0 增至0.5,Z=Ga (图6(a)和(b))的合金弹性常数总能满足晶格稳定性要求;然而,在y≥ 0.4 时,Z=Si (图6(c)和(d))和Ge (图6(e)和(f))的合金C′已减小到负值,即C11<|C12|,具有力学不稳定性,因而更容易发生L21-D022相变.对比图3和图6,不难得出,无论从能量还是力学角度上看,磁无序均降低了3 种合金L21相的稳定性,但也促进了D022相的相对稳定性,导致了L21-D022的MT 行为.

表2 FM 状态下L21-Co2CrZ (Z=Ga,Si,Ge)合金单晶弹性常数(C11,C12,C44,C ′=(C11—C12)/2)、A=C44/C 及多晶G 和E 的EMTO 计算结果与源于文献[36,42]理论值的对比Table 2.Single-crystal elastic constants (C11,C12,C44,and C ′=(C11—C12)/2),elastic anisotropy (A=C44/C ′),G,and E of the FM L21-Co2CrZ (Z=Ga,Si,Ge) alloys are shown in comparison with the available theoretical results from Refs.[36,42].

图6 FM 状态下L21-Co2CrZ (Z=Ga,Si,Ge)合金单晶弹性常数(C44 和C ′=(C11—C12)/2)和A=C44/C 随y 的变化关系 (a)(b) Z=Ga;(c) (d) Z=Si;(e) (f) Z=GeFig.6.Single-crystal elastic constants (C44 and C ′=(C11—C12)/2) and elastic anisotropy (A=C44/C ′) of the FM L21-Co2CrZ (Z=Ga,Si,Ge) alloys change with respect to the magnetic disordering degree (y):(a) (b) Z=Ga;(c)(d) Z=Si;(e) (f) Z=Ge.

在图7 中,FM 状态下L21-Co2CrGa1—xSix和L21-Co2CrGa1—xGex(0 ≤x≤ 1)合金的弹性常数均满足力学稳定性要求.对于Co2CrGa1—xSix合金,随着x的增大,C′和C44增大、而A减小,说明C′相对x的变化速度更快些,即其对合金相稳定性随成分的变化也起到了更重要的贡献.对于Co2CrGa1—xGex合金,随着x的增大,C′同样增大、而C44减小,结果导致A随x的增大单调减小,C′和C44因而对它们相稳定性随成分的变化都具重要意义.两种合金体系G和E对x的变化趋势与其C′-x曲线相同,说明Si 和Ge 掺杂均能提高Co2CrGa 合金L21相多晶弹性模量,从而有利于促进体系相稳定性.0 K 下,各四元合金组分同样具有L21相稳定结构.结合图3 理论结果,可推测磁无序的增大也将会导致该相相对D022相的电子总能逐渐增大,最终高于后者.在不考虑能量其他温度依赖性因素的情况下,当这些四元合金随温度的降低,逐渐由PM 转变到FM 状态的过程中,磁有序化则反过来最终导致L21相的电子总能低于D022相,从而有助于其发生D022-L21的RMT行为.

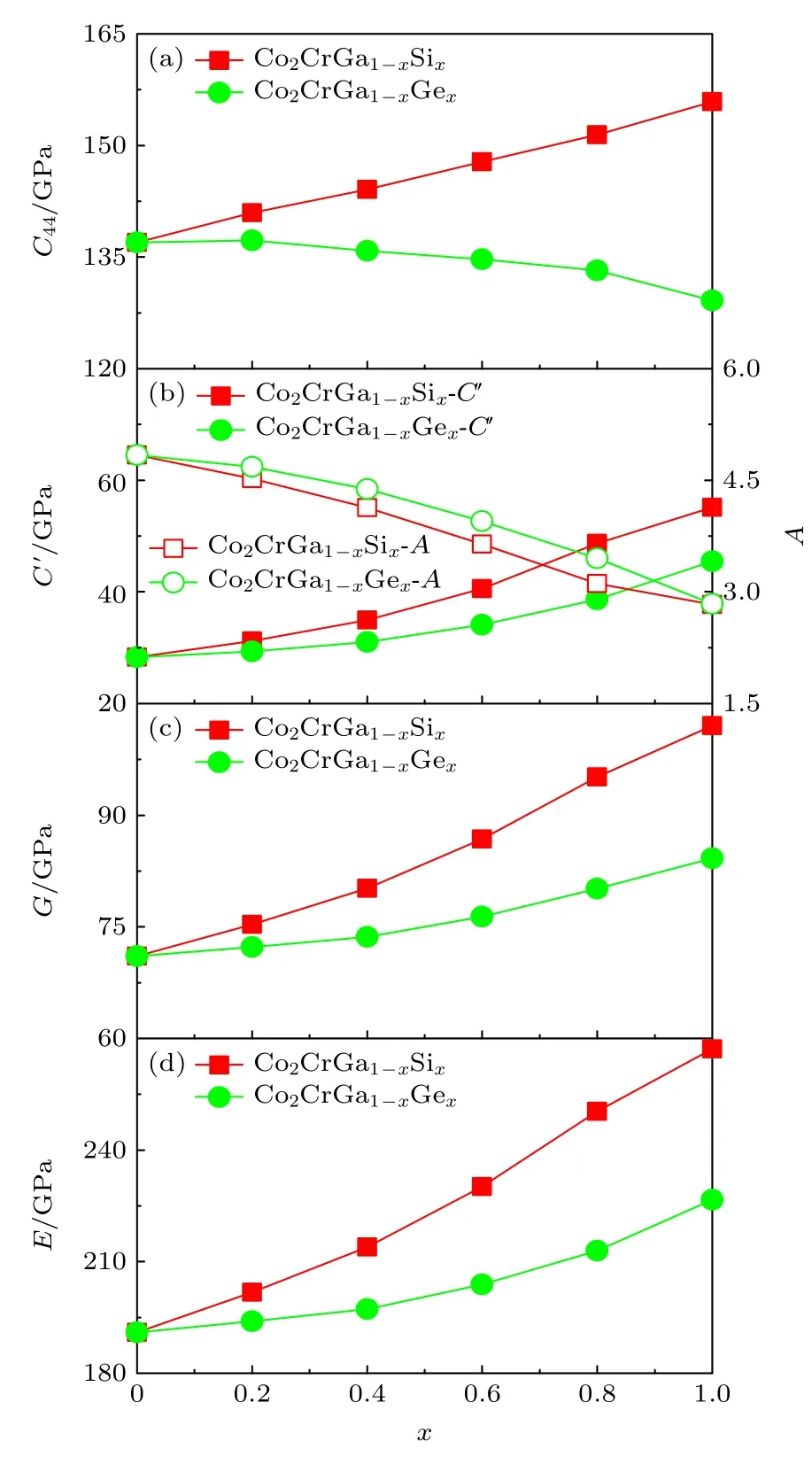
图7 FM 状态下L21-Co2CrGa1—xSix 和L21-Co2CrGa1—xGex(0 ≤ x ≤ 1)合金单晶弹性常数(C44 和C ′=(C11—C12)/2)、A=C44/C 及G 和E 随x 的变化关系 (a) C44—x;(b) C ′—x和A—x;(c)G—x;(d) E—xFig.7.Single-crystal elastic constants (C11,C12,C44,and C ′=(C11—C12)/2),elastic anisotropy (A=C44/C′),polycrystal shear modulus (G),and Young’ modulus (E) of the FM L21-Co2CrGa1—xSix and L21-Co2CrGa1—xGex (0 ≤ x ≤ 1) alloys change with respect to x:(a) C44—x;(b) C ′—x and A—x;(c) G—x;(d) E—x.

3.5 电子结构

为了探讨FM 和PM 状态下Co2CrZ(Z=Ga,Si,Ge)合金L21和D022相相对稳定性的电子结构机理,分别计算了它们总电子态密度(DOS)及Co,Cr 和Z原子的局域DOS,如图8 所示.这里,对于D022相,DOS 计算采用各合金L21相相同的晶格体积;参考图3 计算结果,对于Z=Ga 的合金,c/a=1.2,而Z=Si 和Ge 的合金均有c/a=1.3.根据Jahn-Teller 不稳定性效应[24,43],费米面附近自旋向下DOS 越多,说明该体系相对能量越高,则越不稳定.因此,本文重点分析费米面附近的DOS.

在各FM 合金的费米面附近(图8(a),(e)和(i)),L21相自旋向上的总DOS 均出现了一个显著的峰值,而自旋向下DOS 非常小,自旋极化率均超过90%,证实其L21相的确具有接近半金属性.此外,相比D022相,3 种合金L21相自旋向下的DOS 均更小,对应L21相能量则相对更低、体系更加稳定,因此该立方相对应着它们的基态结构.在各PM 合金的费米面附近,L21相的总DOS 均具有明显的峰值.然而,在D022相,该峰发生劈裂,分布于此处的DOS 被重新分布在更高或更低能量轨道上,结果导致费米面附近形成一个赝带隙,该处的DOS 相对L21相明显减少,能量相对更低.因此,3 种PM 合金具有D022相稳定结构.

图8 FM 和PM 状态下L21-和D022-Co2CrZ (Z=Ga,Si,Ge)合金电子总态密度(DOS)及Co,Cr 和Z 原子局域DOS 的对比:(a)—(d) Z=Ga;(e)—(h) Z=Si;(i)—(l) Z=GeFig.8.Total electronic density of states (DOS) and local density of states of Co,Cr and Z atoms of the Co2CrZ (Z=Ga,Si,Ge)alloys with both the FM and PM L21 and D022 phases:(a)—(d) Z=Ga;(e)—(h) Z=Si;(i)—(l) Z=Ge.

当Co2CrZ合金随温度的升高逐渐由FM 转变到PM 状态的过程中,在费米面附近,L21相自旋向下的DOS 均会增多,则体系能量相对升高(图3),对应着C′(图6)也会发生软化,说明磁无序度的增大逐渐削弱了合金L21相的相对稳定性,促进了合金发生四方晶格变形.在不考虑能量其他温度依赖性因素的情况下,根据Jahn-Teller 不稳定性效应[43],我们证实了,磁无序度的增大有利于Co2CrZ合金D022相的电子总能低于L21相,从而发生L21-D022的正常MT;反过来,磁有序度的增大则有利于其L21相的电子总能低于D022相,导致D022-L21的RMT 行为出现.

对比Co,Cr 和Z原子的局域DOS,发现合金Co2CrZ总DOS 随晶格和磁有序结构的变化主要源于Co 和Cr 原子,尤其Co 原子,其贡献似乎最大.对于Z原子,由于其在费米面附近DOS 相对较少,因此对合金总DOS 及其随晶格和磁有序结构的变化影响不大.