贝叶斯深度神经网络对于核质量预测的研究

娄月申 郭文军†

1) (上海理工大学物理系,上海 200093)

采用贝叶斯深度神经网络对液滴模型进行优化改进,并运用KL (Kullback-Leibler)散度与变分推断的方法使得模型便于实现.以最新的原子核数据(AME2020)中2457 个有精确值的原子核(Z ≥8 和 N ≥8)作为总数据集,随机选取其中80%的数据为训练集用于模型训练,通过预测余下的20%进行模型验证.最终两个数据集的误差均方根(RMS)基本相等,而且全部数据的RMS 从2.9894 MeV 降到0.5695 MeV,下降了80%,呈现出较好的结果.此模型进行了输入参数上的改进(区域限定策略),使得未知核(Z =118—126)可以被限定在一个固定的区域内,从而提高了预测的准确性.为了验证这一性质,对实验数据(Z =100—117)进行了预测计算,结果也与实验值符合得很好.最后使用该方案对未知元素 Z =118—126 进行了预测,为以后寻找新元素提供了新思路.

1 引言

原子核内部的结构信息和动力学信息是核物理研究的重要任务.而且对原子核结合能的准确认识,在天体物理学中也有着极为重要的作用[1–5].原因是,结合能的准确描述可以用来帮助理解恒星的形成、演化及其最终的命运.因此,凭借与天体物理的精密联系,核物理可帮助理解宇宙中的元素,也可相应地提供未知元素的预测.在两个学科所定义的物理量中,核质量的重要性不言而喻,因为这个物理量包含了所有的强相互作用量.而且,原子核的质量与结合能是原子的基本属性,可作为识别不同原子核的一种可靠的方式,类似于指纹识别.此外,精确的核质量测量也可应用于核物理以外的各个领域,如计量学、量子电动力学及元电荷的测量[6–8].在核天体物理学中需要一些可靠的性质,如原子质量、半衰期和不稳定核的反应截面.而在这些基本性质中原子核质量为一个重要的量,它对于估计核转变速率、能量以及理解宇宙中元素的丰度分布都起到了至关重要的作用.但是实验测量目前有着些许不足,如r-过程路径实验在一些核素的测量中有不尽人意的表现,而且大多数的原子核都在实验已知的区域之外.而且,核结构还有一个重要的挑战,即靠近“滴线”边界的计算.因此,使用理论方法代替实验方法进行相应的计算是不可避免的.此外,准确地确定质量值对测试Cabibbo-Kobayashi-Maskawa 矩阵的统一性十分重要,但现今仍存在3 个主要问题:1)如何产生丰中子原子核;2)如何将SMS(Schottky mass-spectrometry)的时间范围扩展到寿命较短的核上去;3)如何得到不稳定的丰中子原子核,如在“等待点”,这对于加深理解r-过程有着极其重要的作用.虽然在亥姆霍兹重离子研究中心(GSI)的近期实验中,已找到了解决第一与第二个问题的初步方法.但对于第三个问题,目前的GSI 设备还没有很好的解决方案[9,10].因此,还是需要依赖于核质量的理论模型,来预测未知但重要的原子核的核质量.所以,全局核质量模型一直是主要的研究目标.

当下,全局核质量模型大致可分为两类:微观模型与宏观-微观模型.微观模型如Hartree Fock Bogoliubov (HFB)[11]和相对论平均场模型[12].其中,前者可以很好地表现出核子之间的配对相关性,后者则可以很好地描述结合能对同位旋的依赖关系,这使得此模型可以可靠地应用于奇异原子核的理论计算.宏观-微观模型如Royer’s 公式[13],该模型推导出976 个奇异核;Thomas-Fermi 模型[14]在Z≥88的范围内有着很好的计算结果,但是在全局范围内有着很大的偏差;Duflo and Zuker (DZ)模型[15]有着良好的外推能力与计算结果,但是年代过于久远;有限力程小液滴模型(FRDM)[16,17]与Weizsäcker-Skyrme (WS)模型[18]考虑了变形对宏观能及镜像核约束的影响,并将宏观能的同位旋相关分量近似到Woods-Saxon 势的深度;Warsaw局域重核模型 (HN)[19]在描述重核方面有着很好的优势;WS3+[20]和WS4+[21]也是两个重要的模型,它们使用的是径向基函数 (RBF)[20].然而,上述模型的计算值对现有数据的计算以及预测与实际都相差了几MeV,或者只在一定范围内有效,虽然改进后有了一些提升,但是在超过适用范围后往往就可能出现较大的偏差,因此预测效果就会有所折扣.

在全局核质量理论计算的研究目标驱使下,到目前为止,各类模型都有了很大的进展.其中就包括液滴模型(LDM)[16]的改进.虽然液滴模型很简单,但它经过不断的改进,计算准确性也在不断地提升.原因是,LDM 认为原子核是一个不可压缩的液滴,由质子和中子两种量子流体组成,计算的结合能随质子和中子的变化而平稳变化.而根据Strutinsky’s 能量定理[22],结合能由两部分组成:第一部分大而平滑,第二部分小而可变.LDM 虽然成功拟合出了第一部分,但却无法解释壳隙周围的波动.

以改进第二部分结合能存在的问题入手,通过对LDM 的改进,本文实现了新的理论计算方法.现在所知的理论计算方法有3 种:传统方法、第一性原理及时下最流行的机器学习方法.传统方法因有大量的猜测,所以大多准确性不足.第一性原理方法基于核子之间的相互作用,计算原子核的结合能,虽然可靠但是有效性与程序的可实现性有待提高.而机器学习方法,在实验能提供越来越多可靠数据的基础上,以机器学习作为模型或者改进优化,来评价和预测所获得的结果,更加的可靠而且高效,可用来解释由于核相互作用的影响而产生的质量波动及对未知区域的预测.现今有很多强大的统计学习方法,其中机器学习方法是使用最频繁最有效的.机器学习也有很多的选择,如人工神经网络(ANN)[23]、贝叶斯神经网络(BNN)[24]、支持向量机(SVM)[25].但由于BNN 是使用概率方法进行建模,因此有着量化不确定性的能力,所以在现有基础上可以更加可靠地预测未知元素.得益于现今硬件的发展,BNN 进行了相应的改进,提升为贝叶斯深度神经网络(BDNN).神经网络对于结果和决策过程的解释可通过输入参量进行大致表现,可是由于传统的神经网络的参量为一个确定的值,所以只能在确定的范围内有好的结果,跳出确定范围后却有着难以预估的偏差.但BDNN 有所不同,其使用概率方法提供了一个函数输出的完整分布并可以识别预测中的不确定性,可在置信区间内确定出更加精确的预测值,很适合进行需要外推的任务[26].另外,用于训练的实验数据也有着不可避免的误差,BDNN 对网络参数的概率分布处理,可以很好地解决这一问题,因此在假设有其他未知不确定性的影响下,可以实现可靠的预测,也不易出现过拟合的情况[27].

本文使用宏观-微观模型的思想对全局核质量模型进行优化,并改进了输入参量.提出使用区域限定策略为输入参量的LDM+BDNN 模型,提升了已知原子核的理论计算能力以及对未知核的外推能力.在已知的数据中表现良好,并实现了全局模型的改进与原子核可探测范围的预测修正.

2 核质量的贝叶斯深度神经网络方法

2.1 理论模型

在模型建立的经验上,宏观-微观方法在解释核质量计算的波动部分取得很好的成效,它利用微观修正来解释宏观模型所缺失的复杂物理现象[28].本文基于上述方案创建了一种新的算法,即LDM+BDNN,主要用于未知核的预测.LDM+BDNN 模型分为宏观、微观两个部分.模型公式为

其中,宏观部分为LDM 模型,微观部分为δLDM.LDM 模型的定义如下[29,30]:

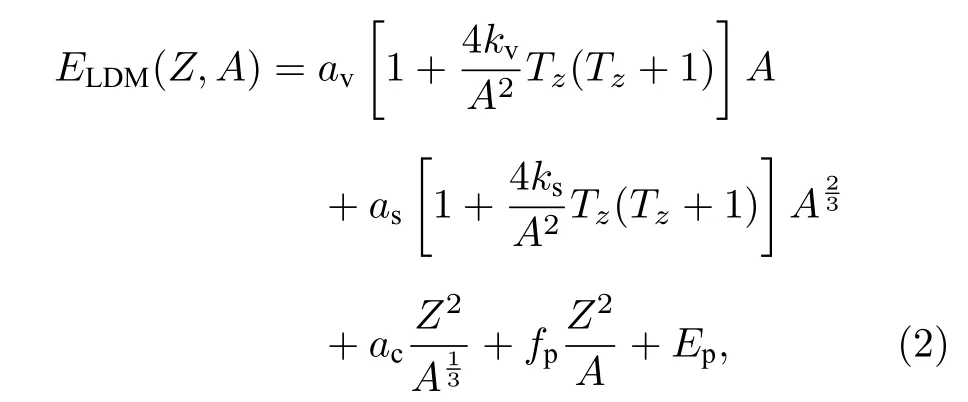
其中,A,Z,Tz为质量数、质子数及同位旋的第三分量;av,kv为体积能的同位旋依赖;asks为表面能的同位旋依赖;ac为库仑能;fp为对称能.

式中dn,dp和dnp为奇偶效应中的可调参数.

液滴模型的所有可调参数通过最小二乘法来确定,所用的数据为符合Z≥8 和N≥8条件的2457 个原子核,这些核均来自于最新的原子核质量评估(AME2020)[31].最小二乘法X2函数为

拟合后的结合能误差均方根为2.9894 MeV,如图3 所示.结果表明,该模型在双闭壳核中存在较大偏差,并有较大波动,显示出了LDM 的缺陷.本文旨在尽可能地模拟结合能的波动部分δLDM.

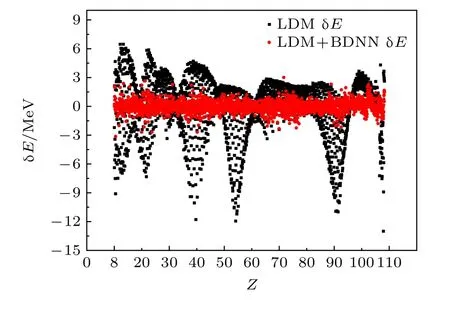
图3 δ E 为2457 个核素的实验值与理论计算值的误差均方根,其中黑点为LDM 模型的理论计算值,红点为LDM+BDNN 模型的理论计算值Fig.3.δ E is the root mean square error of the experimental values and theoretical values of 2457 nuclear,the black spots are theoretical calculation value of LDM model,red dots are the LDM+BDNN theoretical calculation values of the model.

在(1)式中,本文将δLDM视为统计推理问题.概率解释方法主要分为两种:频率派和贝叶斯派.频率派认为,抽样如果是无限的,那么决策规则就可以清晰地表现出来.数据作为可重复的随机样本,有一定的频率.因此所建立模型中的参量为一个可固定的常量.但贝叶斯派有不同的看法,他们以概率的方法处理未知的量,参数应作为一个概率分布,不应作为一个常量,这样才可以得到更准确的结果.贝叶斯定理如(5)式所示,它提供了给定数据集D与给定假设H之间的联系[32].

式中,p(H|D)是给定数据集D假设为真的概率,p(H) 为先验概率,p(D|H)为似然概率.

使用 (x,t)≡D作为相关的输入输出数据,ω ≡H表示完整的模型参数,后验概率则定义为[33]

其中,p(x,t|ω) 为似然概率,p(ω) 为参数ω的先验分布.

本文将深度神经网络模型定义为

式中,模型中的参量为ω={a,bk,ck,dkj,ej,fji};H1和H2为隐含层节点数;n为输入参数,包括(Z,A,Z−Z0,Z−Z1,N−N0,N−N1).在输入参数n中Z,N和A分别为给定原子核的质子数、中子数及质量数.N0,1和Z0,1表示相应的幻数.分别为(N) 8,20,50,82,126,184 以及(Z) 8,20,50,82,126.而N0,1(Z0,1)的值是通过给定原子核在它附近上下左右的4 个幻数确定的(见图1),此为本文新改进的区域限定策略.具体思想为,将一个核素通过与其邻近的4 个幻数进行计算得到一个独特的限定区域的效果.此方法可以提高各个核素的差异性,并且可以在外推预测时,将外推近似为内推,极大地增强了预测的稳定性.

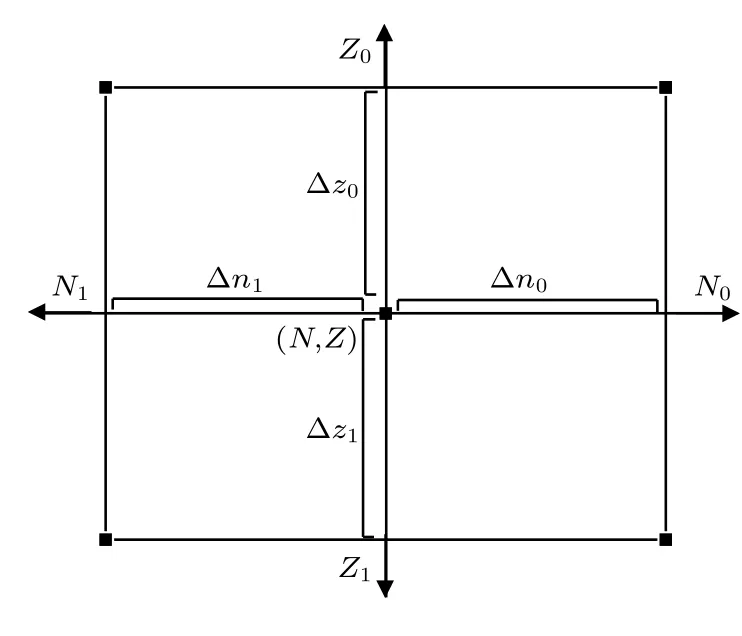
图1 假设原点为给定原子核,取上下左右4 个幻数与其的差值作为限定条件,近似地将给定核限定在一个固定范围内,进而起到提高稳定计算与外推未知核结合能的作用Fig.1.The origin is assumed to be a given nucleus,and the difference between the four magic numbers above,below,left and right is taken as the limiting condition to approximately limit the given nucleus within a fixed range,thus improving the stability calculation and extrapolating the binding energy of unknown nuclei.

表1 液滴模型所有参数的最佳值Table 1.The best value of all parameters in the LDM.

深度神经网络的结构示意图如图2 所示.

图2 一个双隐含层的贝叶斯深度神经网络,其中有6 个输入参量(Z,A, Z−Z0,1 , N−N0,1)和一个输出参量 F=δLDM Fig.2.A double hidden layer Bayesian deep neural network.six input parameters are (Z,A, Z−Z0,1 , N−N0,1)and the output parameter is F =δLDM.

2.2 模型训练

正如上述所讲,宏观部分使用LDM 体现,但并不能很好地解释原子核结合能的所有变化,因此使用BDNN 来代替修正原子核结合能剧烈波动的部分(δLDM).在确定好LDM+BDNN 方法的基础之后,就可以开始进行模型训练了.首先在最新的原子核数据(AME2020)[31]中提取2457 个有精确数值的原子核结合能,原因是可以最大程度地削减错误数据带来的误差,保证模型预测的准确性.然后将所有数据随机打乱并分成80%的训练集和20%的预测集,用来验证模型是否准确.计算结果见表2.

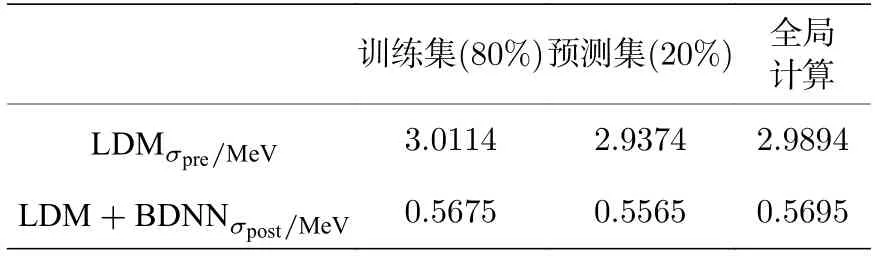
表2 对于AME2020 中提取的2457 个实验数据采用LDM 和LDM+BDNN 模型进行运算.给出训练集(1966)、预测集(491)以及整体核素的理论计算结果与实验值的误差均方根Table 2.LDM and LDM+BDNN models were used to calculate 2457 experimental data extracted from AME2020.The RMS of error between the theoretical calculation results and experimental values of the training set (1966),the prediction set (491),and the whole nuclide are given.

从表2 可以看出,训练集、预测集以及整体的理论计算与实验值的误差均方根基本相同,在表明模型结果良好的同时,在预测方面因区域限定策略的作用也表现出了很好的效果,并且没有出现过拟合的现象,体现出很好的鲁棒性.而在表3 中本文模型与LSD,FRDM,FRDM12,TF,HF-B21,GHFB,KTUY[34],Bhagwat[29],LMNN[28]9 种全局模型进行了对比.在和前7 种微观、宏观-微观模型的结果对比中,即使使用最新的原子核数据进行计算对比,本文的计算结果也大多优于他们.但对比后两个模型,本文的计算结果有些许不足,原因在于本次研究主要聚焦于新的输入策略和BDNN 在未知核外推方面的能力,所以牺牲了部分准确性,不过该问题可以通过引入更多准确的数据进行改进.但是,整体的误差均方根也还在可接受的范围内.

表3 LDM+BDNN 与其他全局模型计算结果的对比Table 3.Comparison of calculation results of LDM+BDNN with other global models.

为了更直观地展现出本文模型的计算效果,给出了计算值和实验值的误差(δE)图,如图3 所示.

从图3 可以看出,原模型在双闭壳核处存在较大的误差,而在加入BDNN 优化后,几乎消除了LDM 模型在计算结合能时产生的一些大的波动,使得几乎所有核素的结合能都能集中在一条紧密的粒子群区域,只存在一些轻微的波动.为了能够更清晰地看出哪些区域的核素存在波动较大的问题,使用幻数对核素图进行了区域划分,绘制了全部2457 个核素以及预测的491 个核素误差均方根的核素图,以确定在哪个区域的核素计算结果较差,如图4 所示.

图4 (a)所有2457 个核素的误差均方根的核素图;(b)随机选取的491 个预测核素的核素图.其中的颜色代表实验数据与LDM+BDNN 计算值的结合能误差均方根Fig.4.(a) The root mean square error radionuclide diagram for all 2457 nuclides;(b) random selection of 491 predicted nuclides.The color represents the experimental data and the calculated value of the LDM+BDNN binding energy of the root mean square error.

研究结果表明,在幻数 50—82 和 82—126两个区域中,核素误差均方根呈明显的规律分布.在50—82的区域中,误差较大的核素呈垂直分布.而在 82—126的区域中,误差较大的核素呈水平分布.并且在超重核的丰中子区域中有着较大计算误差,原因可能是实验数据的不足导致计算结果受到轻核与中核的影响.但从图4(b)可以发现,新提出的区域限定策略与BDNN 的结合发挥了作用,极大地消除了在整体计算中的计算值与实验值的误差,并且在超重核区域也有着很好的改进效果,证明区域限定策略与BDNN 的结合表现出很好的预测稳定性.

为了保证外推预测的稳定性,对模型进行了更加严格的测试,检测轻、中、重核的单、双中子分离能,原因是这两种观测结果可以得到两种不同的结合能之间的差异.在计算了所有核素的单、双中子分离能(Sn,S2n),并与实验值进行比较发现,Sn(S2n)与实验的误差均方根与质量公式所得出的结果一致,两者符合得很好.图5 选取了轻、中、重的Si,Nd 和Hg 原子核及其同位素的单、双中子分离能与实验符合得很好.为更好地体现计算值与实验值的差别,图5 中的插图给出了误差.

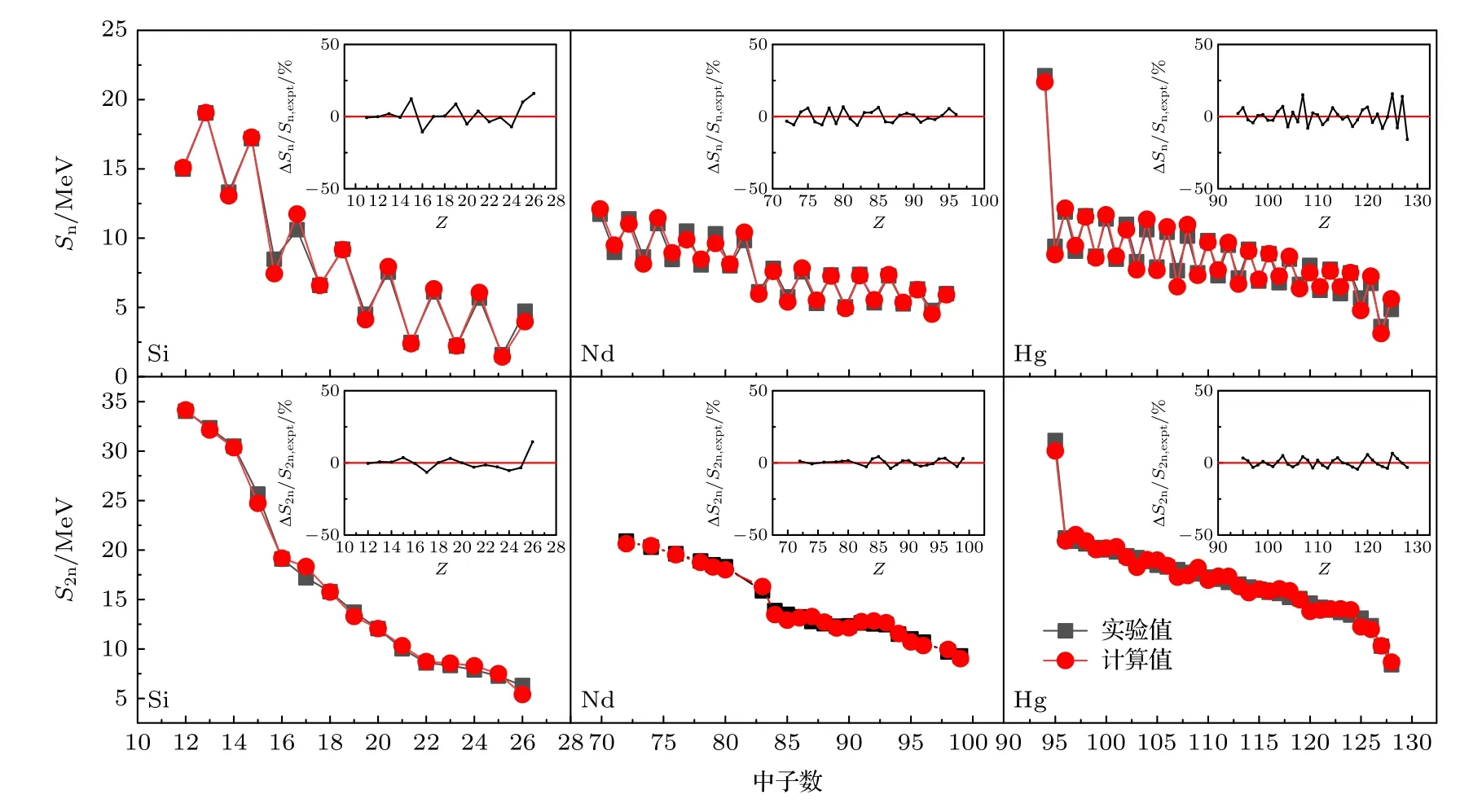
图5 Si,Nd 和 Hg 原子及其同位素的单、双中子分离能随N 的变化,上排为单中子分离能 Sn ,下排为双中子分离能 S2n ,实验值由AME2020 提供(黑色方块),理论计算值由LDM+BDNN 计算得出(红色圆点).插图给出了误差Fig.5.Si,Nd and Hg atoms and their (Sn,S2n) vary with N.The upper row is Sn ,and the lower row is S2n.Experimental values are provided by AME2020 (black squares),and theoretical values are calculated by LDM+BDNN (red dots).The insets are the errors.

核素的奇偶效应也是影响结合能计算的重要参量,从图6 中的结果可以看出,在原有模型的计算结果中,轻核与重核在奇奇核、奇偶核以及偶偶核区域均有较大的偏差,而BDNN 的引入极大地削减了核素的奇偶效应,使得轻、中、重 (8—90,91—180,181—270)核素在不同奇偶组合区域中的偏差近乎拉平.

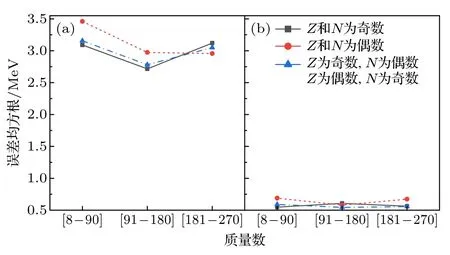
图6 轻、中、重核 (8—90,91—180,181—270) 在奇偶效应区分下的误差均方根示意图 (a) LDM 的计算结果;(b) LDM+BDNN 的计算结果Fig.6.The schematic diagram of root mean square error of light,medium and heavy nuclei (8—90,91—180,181—270) under parity effect differentiation:(a) the calculation result of LDM;(b) the calculation result of LDM+BDNN.

从图4(b)可以看出,区域限定策略与BDNN的结合在预测方面有着很好的表现,因此,为了评估区域限定策略与BDNN 在外推方面的效果,在AME2020 实验数据中选择了训练范围之外Z≥100的核素,将预测值与实验值进行比较,结果如图7所示.可以看出,在训练范围外的重核区域,本文的模型体现了很好的预测结果.只有在Z=112 之后的核素才有些许偏差,其余的核素均贴合得很好,体现出了极强的预测能力,证明区域限定策略与BDNN 极大地提高了模型外推预测的稳定性.原因在于区域限定策略将核素的区域限定保证了区域核素的特殊性,而BDNN 利用概率学的方法提供了模型参量的整体分布(见文献[27] 中的图8),使其可以识别预测中的不确定性,进而得出准确的外推预测值.并且本文计算出了预测原子核结合能的计算误差,如图7(b)所示.在规定好BDNN 的置信区间为95%的条件下,预测计算的平均误差为±2.96%.

有了图7 的验证,本文将外推的区域扩充到未知核的区域中,推断了Z=118—126的超重核,这些超重核的中子数定义为N=Z—2Z.并选取10 个结合能最低的原子核作为确定值,原因是新元素的能量越低相对的稳定性就越强,这样在实验上就更容易发现,结果如图8 所示.

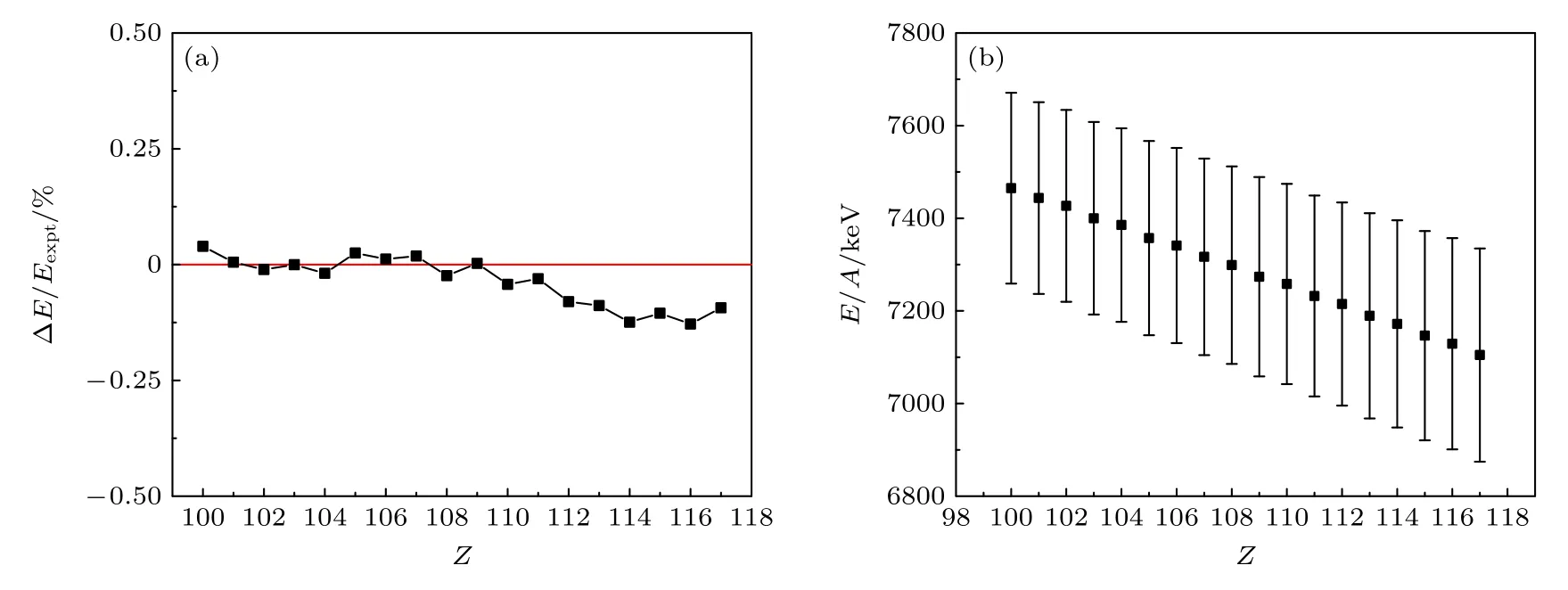
图7 (a)训练范围之外 Z =100—117 的核素结合能最小值的预测值与实验值的误差对比;(b) BDNN 预测值的系统误差Fig.7.(a) Outside the scope of training Z=100–117 nuclide binding energy of the minimum of error comparison of the predicted values and the experimental value;;(b) system error of the BDNN predicted values.

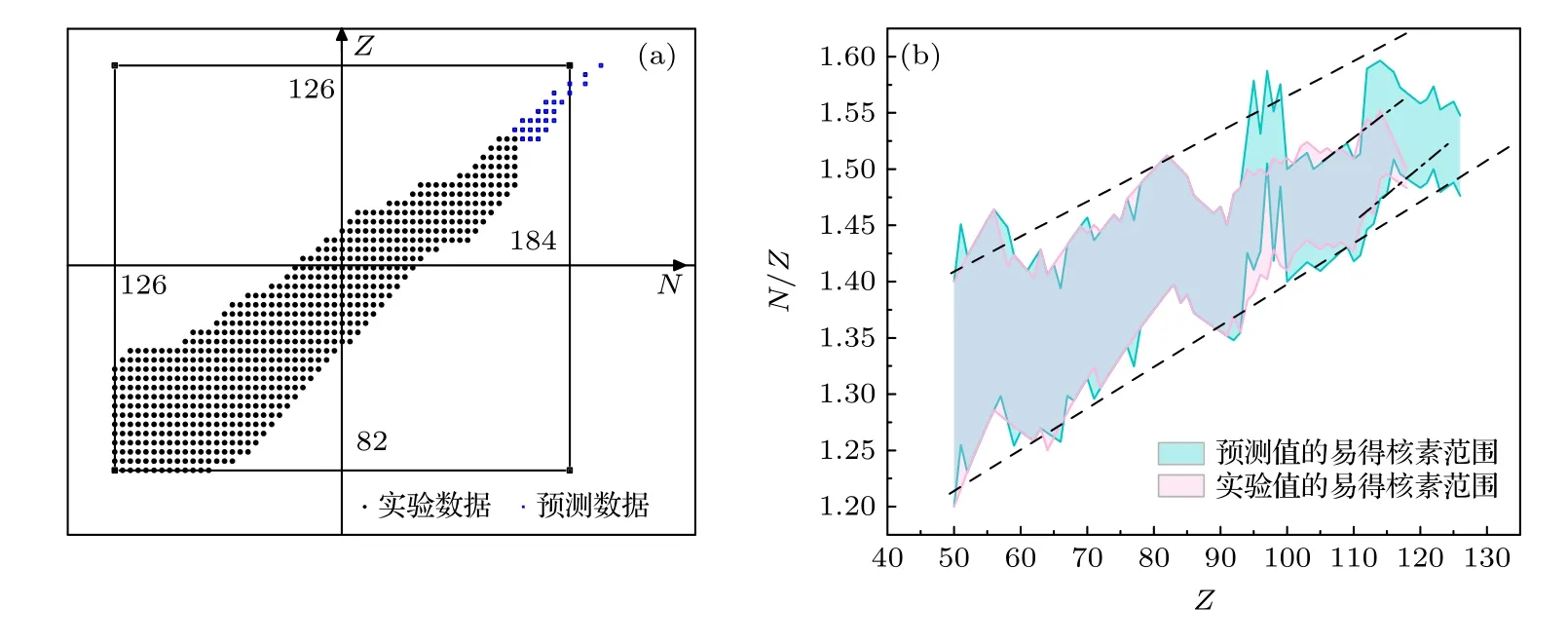
图8 (a)使用区域限定策略与BDNN 的结合,预测在(126,184)区域内未知的超重核,星号为本文预测的未知超重核;(b)外推结果(Z =50—126)与实验结果(Z =50—126)的范围对比,其中红色的阴影为实验值,蓝色为预测值,外部虚线为整体变化趋势,内部虚线为重核变化趋势Fig.8.(a) Predicted the unknown superheavy nuclei in the region (126,184) using the combination of the region limiting strategy and BDNN,the asterisk is the unknown superheavy nuclei predicted;(b) the range comparison between extrapolation results(Z =50—126) and experimental results (Z =50—126).The red shadow is the experimental value and the blue is the predicted value.The outer dotted line shows the overall trend,while the inner dotted line shows the core trend.

从图8 可以看出,与图4(b)相同,在原子核外推预测的能力表现上,LDM+BDNN 模型在区域限定策略与BDNN 的结合下,展现出了极强的预测外推能力.整体核素预测值的变化趋势与实验值基本相同.而且,在超重核区域也依旧保持着相同的变化趋势,证明了在未知超重核预测方面的稳定性,这表明即使在不确定性增加的情况下区域限定策略与BDNN 的结合依旧可以进行合理的预测推断.而如图8(a)所示,本文预测的超重核大多也在规定的限定区域中,进而保证了结果的准确性与稳定性.但是考虑到壳的性质,在超重核区域传统的幻数可能不再适用[35−37].使用文献[35−37]给出的超重核新壳层设定了不同的幻数区域进行预估,结果如图9 所示.可以看出,在不同的壳结构可以得出相似的最低比结合能,但是给出的核素是不同的.表明模型可以得出发现概率最大的核素的比结合能.其次,本文寻找了文献[38−40]中预测的超重核结构,进行了对比验证,结果如图10 所示.可以看出,所有的超重核预测(结合能最低的10 个)都符合得很好.而且,考虑到亚壳对超重核的影响,本文在超重核的预测上重新设计了幻数的限定方法:1)单纯使用亚壳作为区域边界;2)单纯使用主壳层为区域边界;3)将亚壳作为中间区域,使用主壳层作为区域边界.结果发现,在使用亚壳层N=162 作为中间区域时模型表现出了更好的结果,相比其他两种区域边界,预测出的比结合能曲线更加平滑,而且与文献[38−40]符合得更好,也就更有希望被找到,证明本文模型在超重核的预测上有着很好的准确性.

图9 不同幻数的限定区域下,预测超重核的最低结合能Fig.9.The lowest binding energy of superheavy nuclei is predicted under the limited region of different magic numbers.

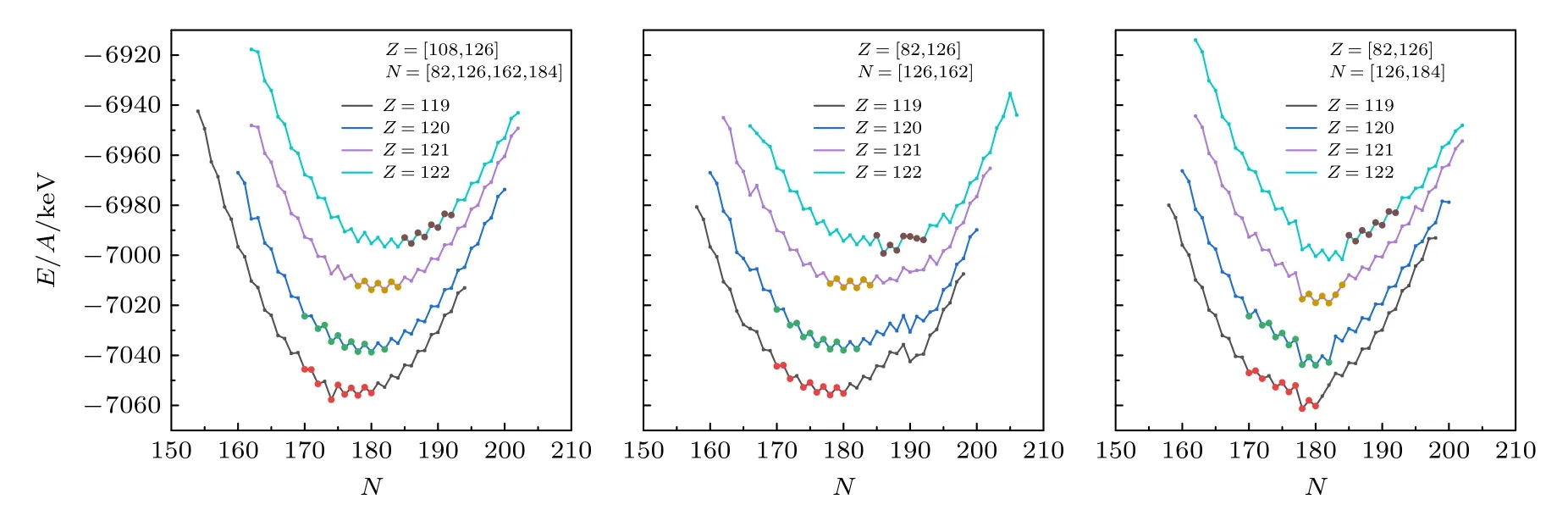
图10 LDM+BDNN 所预测的超重核(线)与文献[38−40]中预测的超重核(点)对比,选取不同的幻数Fig.10.A comparison between the predicted superheavy nuclei (line) and the predicted superheavy nuclei (point) in the Refs.[38−40]),select different magic numbers.

3 结论

综上所述,本文引用了LDM+BDNN 方法与新的区域限定策略来重新定义了一个新的可进行准确预测的理论计算方法.对比AME2012[41],AME2020 的最新数据增加了104 个新核,这降低了各个全局质量模型的计算精度,BDNN 方法以概率的方法处理未知的量,将参数作为一个概率分布而不是一个常量,从而保证在未知的不确定性很大的区域依旧可以得到准确结果,显著地改善了以前的全局模型在预测方面不足的问题.并且,在使用新的区域限定策略的改善下,即使是外推的未知核素,因为被限定在了一个特定的区域内,其稳定性与准确性也得到了很好的保证.因为在限定好固定的区域后各个核素被进行了严格的划分,最大程度地体现了核素的差异性.并且,区域限定策略也可将外推核素近似地转化为内推,体现了很好的稳定性.并且在考虑了形变亚壳的影响下,在不同的壳结构可以得出相似的最低比结合能,虽然给出的核素是不同的.但模型可以得出发现概率最大的核素的比结合能.因此在不超规定范围内进行的外推,都可认为是可靠的.

最终的结果也表明,本文新提出的理论计算方法,不仅显著消除了原有模型在核质量计算时所产生的巨大波动.而且有效地改善了奇偶效应在轻、中、重核素的巨大差异.即使是现有最佳的全局核质量模型,依旧需要进行不断地改进,而且大多数模型在预测未知核的能力上存在不足,最重要的是,一个通用的能量密度泛函也有其建立的困难性.但区域限定策略与BDNN 的结合,为未知核的预测提出了一种新的方案且建立简单,有很大的发展空间.此外,BDNN 方法还可以改进核素的其他性质,如核电荷半径[42]、β-衰变半衰期[43]、裂变产率[44]、总反应截面[45]等.并且,BDNN 经过长时间的发展也有了很多优化近似方法,因此还可以在现有的基础上进行创新.

感谢上海理工大学物理系贾力源教授和张霄吉博士参与讨论,以及西安交通大学郭威博士参与讨论.