基于Boosted-Gold 算法的γ 能谱反演分析*

张双 贺三军 廖峰 罗万 周芷千 高波 刘丽艳 赵修良

(南华大学核科学技术学院,衡阳 421001)

为了利用低能量分辨率探测器γ 能谱分析获取未知放射性核素的特征信息,提高γ 能谱中重峰及弱峰分析的准确性和有效性,本文开展了基于Boosted-Gold 算法的NaI(Tl)探测器γ 能谱分析研究.采用MCNPX建立NaI(Tl)探测器模拟模型,获得了维度201×200 的探测器响应矩阵.基于Boosted-Gold 算法开发了γ 能谱反演程序.实验测量了γ 源22Na,133Ba 和152Eu 的探测器响应能谱,并以不同γ 射线能量、不同能差 (ΔE)、不同相对强度为条件构建了3 组低分辨率模拟γ 能谱,结合响应矩阵及反演程序对实测γ 能谱和模拟γ 能谱进行反演.以IAEA 数据库核素标准特征信息对反演结果进行分析.结果表明:Boosted-Gold 算法对实测γ 能谱特征能量反演误差最大为2.17% (133Ba 源0.276MeV),反演强度与标准强度最大差为0.197(152Eu 源1.408 MeV).对模拟γ 能谱核素特征能量均可准确分析,反演强度与标准强度差值保持在0.01 以内;当增强系数p≤14 时,Boosted-Gold 算法有利于γ 放射性核素的定量分析,对于相对强度大于10%的γ 射线,该算法具有更好的分析准确性.

1 引言

随着γ能谱分析技术在核应急监测、核安全、环境辐射防护等应用领域的深化扩展,对γ能谱分析核素特征信息的准确性和有效性提出更高的要求[1].目前NaI(Tl)探测器因其探测效率高、价格低、易维护等特点,大面积应用于一些实际条件下的γ能谱的测量[2],但受其能量分辨率限制以及测量环境本底等因素的影响,实测γ能谱常常表现为能量相近的射线形成复杂的重峰、强度较弱的核素全能峰完全淹没于本底及康普顿效应当中[3,4],以上不利性态提高了辐射特征信息的分析难度,目前针对低能量分辨率γ能谱的定性定量分析准确性低[5],尤其针对弱峰的定量分析误差可达34%以上[6].因此如何实现重峰及弱峰的分离和识别、提高低分辨率γ能谱分析的准确性和有效性是目前急需解决的问题.

能谱反演技术用于γ能谱分析可有效提高其能量分辨率,增强低分辨率γ能谱核素特征信息的易读性[7,8].现已提出多种γ能谱反演算法,如奇异值分解(singular value decomposition,SVD)算 法[9],最大似然-期望最大化算法(maximum-likeli-hood expectation maximization,ML-EM)[10],Gold 算 法[11],直接解调法(direct demodulate method,DDM)等[12];其中ML-EM 和Gold 算法因具有全局收敛性、解的非负性、收敛速度快等特性,是目前最有效且常用的反演算法[10,11,13];然而Gold 算法相较ML-EM 算法在理解掌握和开发方面更具优势[14,15];在Gold 算法基础上提出的Boosted-Gold 算法[16],进一步提高了收敛速度,解决了前者收敛稳定后无法更进一步提升能谱分辨率的问题.

目前国内外学者分别对多种算法在不同探测器、不同领域下的运用做了验证性研究[9-16],2009 年Rahmand 等[3]将ML-EM 算法用于水下γ放射性核素监测系统的能谱分析,结果表明γ能谱峰总比提高,全能峰计数提高了5.29 倍;2016 年何剑锋等[17]采用Gold 算法,以实测能谱数据验证了采用高斯响应矩阵对γ能谱进行分析的可行性;2019 年,赵日等[18]采用Gold 算法运用于全身计数器γ能谱分析,与Genie2000 软件分析结果比较,表明反演算法优于传统全能峰法;2021 年张双佼等[19]将one-fold Gold 算法用于EJ309 液体闪烁体探测器的响应谱反演,验证了其用于γ能谱分析的可行性以及在n-γ分辨领域的应用潜力.然而更多工作只强调了反演算法用于特定领域γ能谱分析的可行性[17-22],尤其对于Boosted-Gold 算法用于低能量分辨率探测器γ能谱分析的应用研究并未见更多报道.因此,有必要对Boosted-Gold 算法应用于低分辨率探测器γ能谱分析,开展其重峰及弱峰分析的准确性和有效性研究;尽管本研究只针对了较低能量分辨率的NaI(Tl)探测器,但其应用范围与实用性价值较大.

本文为了提高低分辨率探测器γ能谱重峰及弱峰分析的准确性和有效性,开展了基于Boosted-Gold 算法的NaI(Tl)探测器γ能谱反演研究,以期实现对入射γ射线的准确定性定量分析,为利用低分辨率探测器在未知放射性核素的种类及强度分析中提供技术支撑.

2 理论及算法开发

理论上,某一特征能量的γ射线的能谱表现为线状谱[23],即只在特征能量存在幅值,能谱反演的目的是由谱仪测量的脉冲响应谱求解γ射线本征谱,实现γ射线的定性定量分析.入射γ射线与脉冲响应谱之间的关系可如(1)式所示[2,11]:

其中x为入射谱;y为脉冲响应谱;h(ΔE,E) 为探测器的响应函数,表示所测能量为 ΔE的单位能量的γ射线对应于脉冲响应谱中能量E处的相应计数.当h(ΔE,E) 与x(ΔE) 均可积条件下,(1)式可进一步离散化为

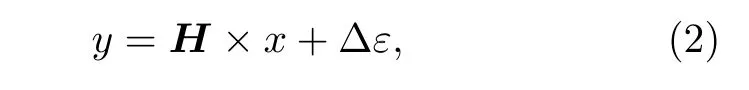
其中 Δε为γ射线测量过程中的误差;H为探测器响应矩阵,如下所示:

维度m,n分别由响应函数离散化程度与步长确定.根据(2)式和(3)式,函数(1)可离散化为

其中误差项 Δε包涵于响应矩阵H中.由于(4)式中误差项的存在以及H中各列之间的强关联性[13],使得该方程组解的问题实际是不适定问题,采用直接求逆方法无法求出有意义的解,通常由特殊反演算法得到待求解.

为了准确求解(4)式,Boosted-Gold 反演算法[16]中以HT左乘(2)式,引入局部松弛系数µ,建立如下迭代过程:

其中n 为构成响应矩阵的响应函数个数,将满足收敛条件解x 的各分量 进行如(7) 式的幂指数非线性增强,并将其作为迭代初值再一次进入(6) 式迭代计算,最终得到满足收敛条件的解.

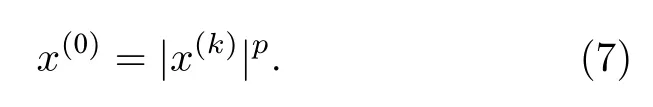
上式中p＞ 1,为幂指数增强系数;根据(6)式和(7)式对算法进行开发,过程如图1 所示:

如图1 所示,算法迭代过程如下:

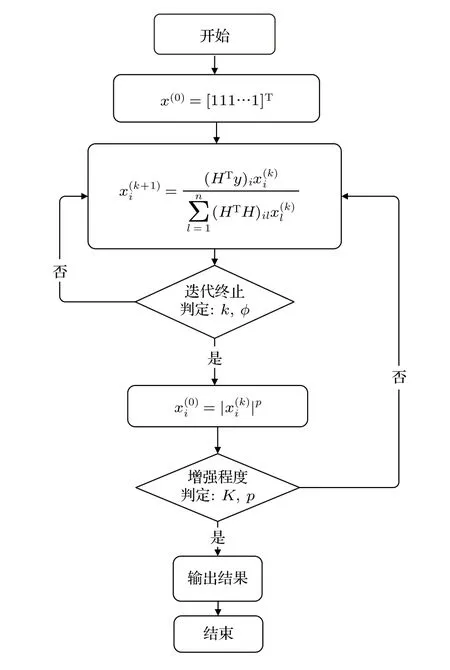
图1 Boosted-Gold 算法计算过程Fig.1.The calculation process of Boosted-Gold Algorithm.

a) 首先,给定初值x(0)、迭代次数k以及迭代终止判定条件φ.

b) 其次,进入迭代过程并进行迭代终止判定.

c) 再次,设定增强次数K及增强系数p进行再一次迭代并进行迭代终止判定.

d) 最后输出结果.

其中初值x(0)中的各分量设定为1;迭代判别条件如(8)式所示:

式中,x(k)为第i次迭代结果,x(k+1)为第i+1 次迭代结果;φ为给定的迭代残差精度.

3 探测器刻度及响应矩阵的获取

3.1 实验系统及γ 能谱测量

γ能谱测量实验系统主要由FJ374 型NaI(TI)闪烁体探测器(40 mm×40 mm),BH1283N 型高压电源,BH1218 型线性放大器(FH0001A 型 机箱),ADC 多道脉冲幅度分析器以及PC 搭建,如图2 所示.实验中γ源到探测器探头的距离为1.5 cm,高压电源电压为420 V,主放放大倍数为20,测量时间120 min,输出信号由4096 道ADC多道脉冲幅度分析器进行数据采集并在PC 端显示;最后对标准γ源22Na,60Co,133Ba,137Cs 和152Eu脉冲响应谱进行了测量,并在相同实验条件下测量了环境本底用于后续数据处理.

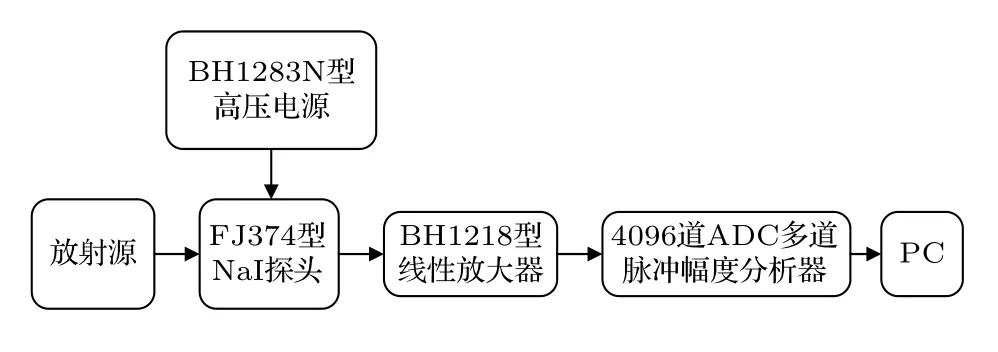
图2 实验平台电子学框图Fig.2.The electronics block diagram of the experimental platform.

3.2 NaI(Tl)探测器能量刻度和分辨率刻度

探测器的能量刻度和分辨率刻度是γ能谱分析的依据,也为NaI(TI)探测器蒙特卡罗建模提供准确参数.能量刻度函数由γ射线的全能峰峰位与对应的特征能量线性拟合获得.为了准确获得标准γ源22Na,60Co,133Ba 和137Cs 全能峰的峰位以及半高宽(FWHM),首先根据实测自然本底对实验能谱进行了本底计数扣除;然后采用Savitzky-Golay 方法对谱数据进行了3 点平滑滤波,消除探测器对γ射线响应统计过程中统计涨落的影响;最后采用一阶导数寻峰方法,获得所测γ源全能峰峰位及半高宽信息;能量刻度如图3 所示.

图3 FJ374 型NaI(Tl)探测器能量刻度Fig.3.Energy calibration of FJ374 NaI(Tl) detector.

图3 中能量刻度函数表征了全能峰峰位(N)与入射γ射线特征能量(Eγ)的线性关系.如(9)式所示:

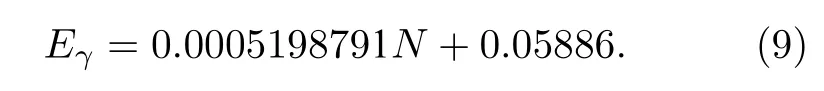
能量分辨率与入射γ射线的能量相关,因此能量分辨率刻度由γ射线特征能量与响应谱对应全能峰半高宽(FWHM)完成,函数表达式如(10)式所示[24]:

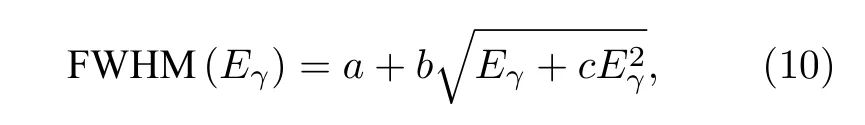
其中a,b,c为待定展宽参数.Eγ为全能峰对应的入射γ射线特征能量,单位为MeV;根据实测标准γ源特征能量及对应全能峰半高宽信息进行非线性待参拟合,获得(10)式待定参数a=0.01607,b=0.02729,c=1.28065,如图4 所示.

图4 能量(Eγ)与半高宽(FWHM)对应关系Fig.4.The correspondence between energy (Eγ) and halfmaximum width (FWHM).

3.3 响应矩阵的计算

响应矩阵的准确性和反演算法的稳定性是进一步降低分析偏差的两方面.为了准确获得NaI(TI)探测器响应矩阵,采用MCNPX 模拟程序构建了探测器模型,建模参数与实验条件保持相同,其中入射γ射线源为点源,与探测器探头距离为15 mm,探测器灵敏体积为厚40 mm、直径40 mm 的柱型,外层铝壳厚度为1.5 mm,反光层MgO 厚度为1.5 mm,如图5 所示.

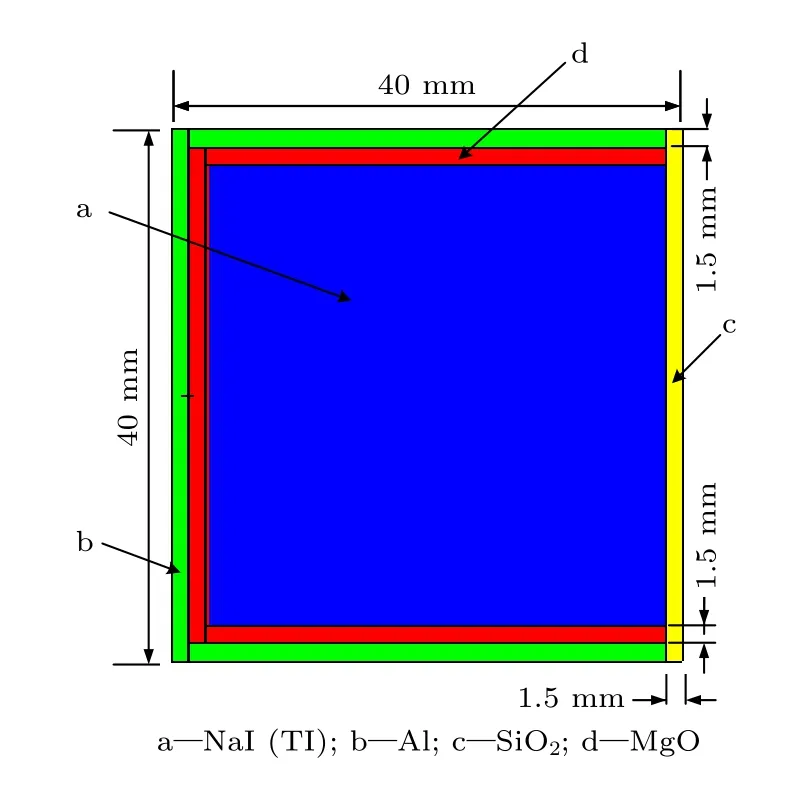
图5 FJ374 型NaI(Tl)探测器仿真模型Fig.5.The simulation model of FJ374 NaI(Tl) detector.

将每个入射单能γ射线响应函数作为构建响应矩阵一个列向量,共由200 个单能γ射线的响应函数列向量构成;模拟过程采用F8 计数卡进行计数抽样为200 道,抽样能量范围为0—2 MeV;各单能γ射线能量随步长0.01 MeV,覆盖能量区间为0.01 至2 MeV;采用(10)式对模拟响应函数进行展宽,最终得到维度为201×200 的响应矩阵,结果如图6 所示.

图6 NaI(TI)探测器响应函数Fig.6.Response matrix for the NaI (TI) detector.

4 γ 能谱反演

4.1 Boosted-Gold 算法反演低能量分辨率γ 能谱的准确性

为了验证Boosted-Gold 算法反演低分辨率γ能谱重峰和弱峰分析的准确性,根据开发的反演算法程序和计算的响应矩阵,对实验测量标准γ源22Na,133Ba 和152Eu 脉冲响应谱进行反演,反演前后结果对比如图7 所示.

由图7 可见,图7(a)中22Na 源只能清晰显现能量为0.511 MeV 的γ射线全能峰,图7(b)中133Ba源特征能量为0.223,0.303,0.384 MeV 的γ射线全能峰被完全淹没,而图7(c)中152Eu 源只有少数全能峰可见,经过反演后γ能谱全谱分辨率均明显提高,全能峰准确显现且峰面积计数可读,对反演结果的准确性进行分析,如表1 所列,其中γ射线特征能量反演结果与标准值误差由(11)式计算:

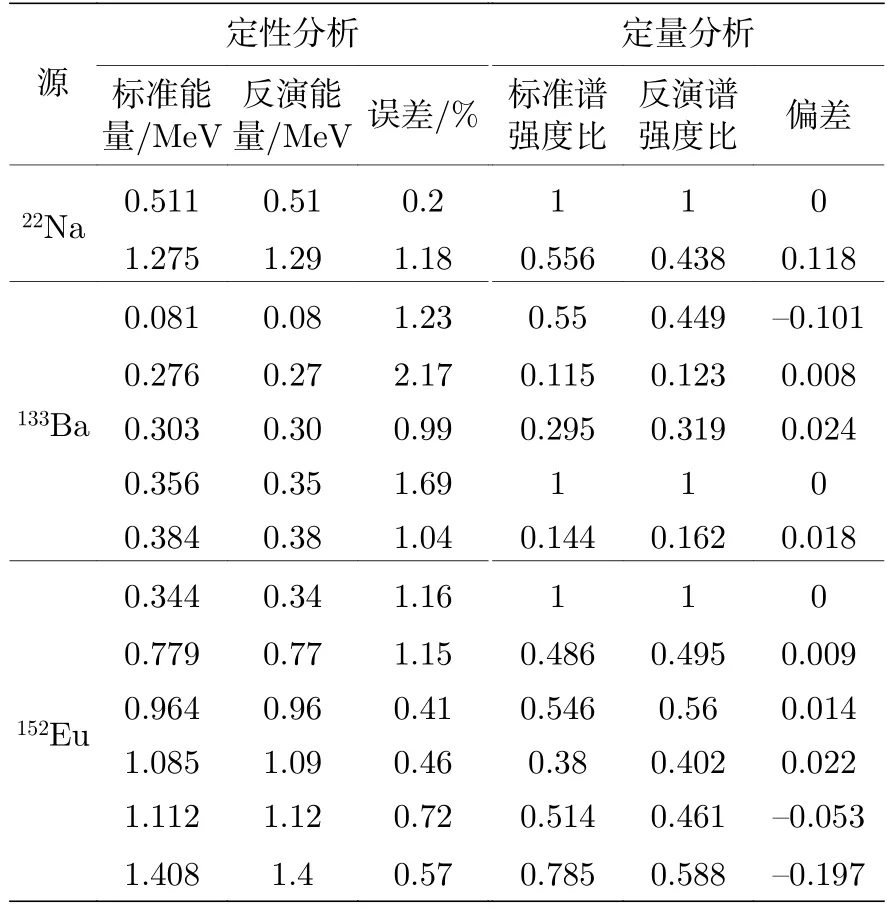
表1 实验谱与反演谱结果分析对比Table 1.Analysis and comparison of the experimental spectrum and the unfolded spectrum results.

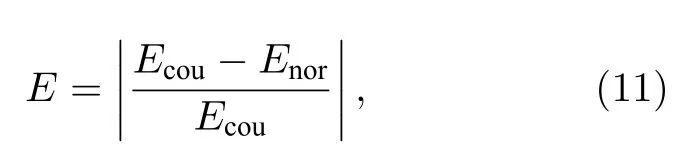
图7 实测γ 能谱与反演能谱的比较 (a) 22Naγ 源能谱反演前后结果对比;(b)133Baγ 源能谱反演前后结果对比;(c)152Eu γ 源能谱反演前后结果对比Fig.7.The comparison between the measured γ energy spectra and the unfolded energy spectrum:(a) Comparison of the results before and after the unfolded of the energy spectrum of the 22Na γ source;(b) comparison of the results before and after the unfolded of the energy spectrum of the 133Baγ source;(c) comparison of the results before and after the algorithm unfolded of the energy spectrum of the 152Eu γ source.

式中,Ecou表示反演后的特征能量,Enor表示标准特征能量,反演强度分析中采用IAEA 核数据库γ放射性核素各特征射线间绝对强度之比作为标准数据,用于验证γ射线全能峰计数收敛结果的准确性.

表1 反演结果表明,γ射线特征能量反演误差最大为2.17%(133Ba 能量为0.276 MeV).反演强度与标准强度最大偏差为0.197,除特征能量为1.275 MeV(22Na),0.081 MeV(133Ba),1.408 MeV(152Eu)的γ射线强度偏差大于0.1 外,其余γ射线反演强度偏差均小于0.06.

反演偏差主要由于以下原因:首先由于反演结果的准确性依赖于响应矩阵的准确性,因此蒙特卡罗模拟响应函数与实际响应函数的差异是造成反演结果偏差的一方面;其次,当低能区全能峰计数收敛不完全时,强度计算过程中认为γ射线特征能量相邻道计数也属于全能峰计数,一定程度上增加了强度计算与标准值的偏差;最后,受限于响应矩阵步长(0.01 MeV),当两种γ射线能差小于响应矩阵步长时,将无法分析该两种特征γ射线,强度反演结果将大于标准值,如对133Ba 的特征能量为0.079 和0.08 MeV 的γ射线分析.

4.2 Boosted-Gold 算法反演低能量分辨率γ 能谱的准确性和有效性

实测γ能谱反演结果验证了Boosted-Gold 算法对低分辨率探测器γ能谱重峰和弱峰分析的准确性,为了进一步研究Boosted-Gold 算法用于低分辨率探测器γ能谱分析的准确性和有效性范围,以MCNPX 建立的NaI(TI)探测器模型,根据γ射线不同相对强度、不同能量(Eγ)、不同能差(ΔE)模拟获得了三组低分辨率探测器γ能谱,其中入射γ射线能量由(12)式确定[25]:

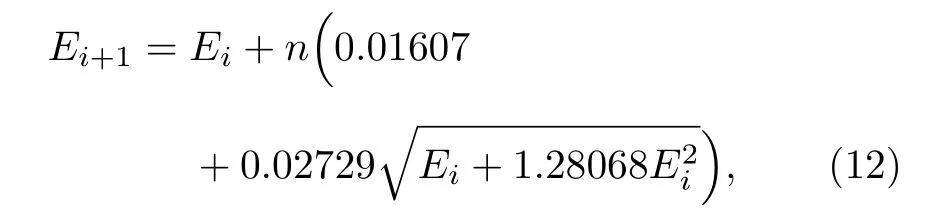
其中n取值为1,Ei为第i种单能射线能量,模拟谱分别有4,6 和8 种不同γ射线能量,获得γ能谱射线最小能差为0.03 MeV,相邻γ射线强度最大比为1:0.3;利用开发的反演算法程序和获取的响应矩阵对模拟γ能谱进行反演;增强因子p=4,进行10 次增强过程,每次进行1000 次迭代,反演前后结果对比如图8 所示.

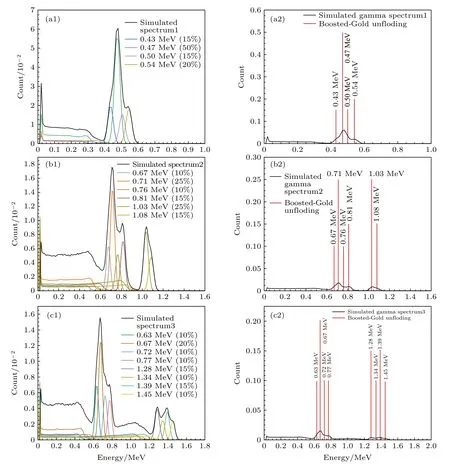
图8 模拟γ 能谱反演前后结果对比 (a1) 4 种能量γ 射线模拟谱;(a2) 4 种能量γ 射线模拟谱反演前后结果对比;(b1)6 种能量γ 射线模拟谱;(b2) 6 种能量γ 射线模拟谱反演前后结果对比;(c1) 8 种能量γ 射线模拟谱;(c2) 8 种能量γ 射线模拟谱反演前后结果对比Fig.8.The comparison of between the results before and after the unfolding of the simulated γ energy spectrum:(a1) The simulation spectrum of gamma-rays of 4 energies;(a2) the comparison between the results before and after the unfolding of the simulated spectrum of energy γ-rays of 4 energies;(b1) the simulation spectrum of gamma-rays of 6 energies;(b2) the comparison between the results before and after the unfolding of the simulated spectrum of energy γ-rays of 6 energies;(c1) the simulation spectrum of gamma-rays of 8 energies;(c2) the comparison between the results before and after the unfolding of the simulated spectrum of energy γ-rays of 8 energies.

如图8(a1)、图8(b1)和图8(c1)三组混合γ能谱中,强度较弱的γ射线全能峰严重重叠甚至被相对强度较高的γ射线全能峰掩盖,反演结果分别如图8(a2)、图8(b2)和图8(c2)所示,各全能峰清晰显现且计数均收敛于一道,入射γ射线能量及全能峰计数均可直接读取,反演谱分析结果如表2 所列.

表2 模拟谱与反演谱结果对比Table 2.Comparison of the simulated spectrum and the unfolded spectrum results.

由表2 可知,γ能谱中被淹没的全能峰均可被准确反演,γ射线反演能量与入射能量一致;反演强度与标准强度最大差为0.014,其余各全能峰反演强度与标准强度偏差均小于0.01.图8(a1)中能量为0.5 MeV 的γ射线反演强度偏差最大为0.007,其余γ射线反演强度偏差均小于0.002.图8(a2)中能量为0.71 MeV 的γ射线强度反演结果偏差最大为0.004,而能量为0.67 和0.76 MeV 的γ射线强度反演偏差为0.003.图8(a3)中能量为1.45 MeV的γ射线强度反演偏差最大为0.014,且能量为1.28,1.34,0.67 和0.72 MeV 全能峰强度与标准强度偏差均大于0.005.可见,随着入射γ射线增多,γ射线强度反演的准确性变小,且反演准确性与γ射线强度成正比.

当γ射线相对强度小于10%时,反演强度均小于标准强度,且相对强度越小,反演强度与准确强度偏差越大,造成这一结果的原因在于,反演过程中非线性幂指数增强系数p使得谱数据中占比较小的分量相对更小,导致迭代过程该分量更快向0 收敛,表现在反演结果中γ射线强度反演结果偏小,且γ射线相对强度越小偏差将越大.

4.3 增强系数p 对弱峰及重峰结构解析能力的影响

Boosted-Gold 反演算法中非线性幂指数增强系数p的引入是为了克服Gold 反演算法收敛稳定后无法进一步提升能量分辨率的问题;然而实验发现,增强系数p在进一步提升γ能谱重峰和弱峰分离的同时,分析结果的准确性随p变化较大,尤其对于相对强度小于10%的γ射线;为了进一步说明增强系数p对弱峰或重峰结构的解析准确性的影响,构建了能量和相对强度分别为0.43 MeV(3%),0.46 MeV(50%),0.5 MeV(5%),0.82 MeV(35%),0.87 MeV(7%)的低分辨率γ能谱,研究在不同p值下相对强度小于10%的γ射线反演结果的准确性,如图9 所示.

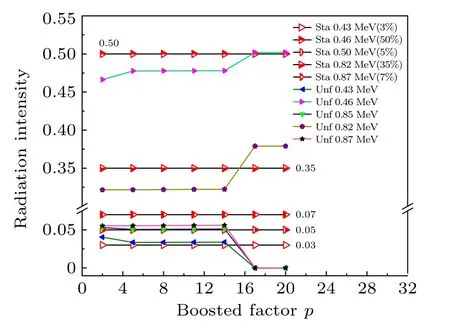
图9 不同p 值下标准相对强度数据与反演数据的对比Fig.9.The comparison of the standard relative intensity data and the unfolded data at different p-values.

反演结果表明,当p≤14 时各γ射线强度的反演结果基本保持恒定,有利于γ能谱的分析,特别是弱峰;当p＞14 时,反演结果准确性降低,相对强度小于10%的γ射线全能峰计数进一步向0 收敛,相对强度较大的γ射线计数进一步增加,最终全谱只有相对强度较大的γ射线全能峰被保留且保持恒定,将无法完成相对强度小于10%的γ射线的分析识别.

5 结论

为了利用低能量分辨率探测器γ能谱分析获取未知放射性核素的特征信息,提高γ能谱中重峰及弱峰分析的准确性和有效性,本文开展了基于Boosted-Gold 算法的NaI(Tl)探测器γ能谱分析研究.首先采用蒙特卡罗方法建立了NaI(TI)探测器模型,以此构建了NaI(TI)探测器响应矩阵;其次根据Boosted-Gold 算法理论开发了能谱反演程序;然后根据响应矩阵和开发的反演算法程序对模拟γ能谱和实测γ能谱进行反演;以实测γ源22Na(0.511 和1.275 MeV),133Ba(0.081,0.276,0.303,0.356 和0.384 MeV)和152Eu(0.344,0.779,0.964,1.085,1.112 和1.408 MeV)脉冲响应谱,验证了Boosted-Gold 算法反演低分辨率探测器γ能谱的准确性;以不同γ射线相对强度、不同入射能量(Eγ)、不同能差(ΔE)构建了三组低分辨率探测器γ能谱,进一步验证了其反演低分辨率探测器γ能谱重峰及弱峰的准确性和有效性;最后进一步明确了非线性增强系数p对重峰及弱峰结构分析准确性的影响.

实测γ能谱反演结果表明:Boosted-Gold 算法对γ射线特征能量反演误差最大为2.17%(133Ba 能量为0.276 MeV);反演强度与标准强度最大偏差为0.197(152Eu 能量为1.408 MeV).能谱中γ射线强度最大比为1:0.115(133Ba 特征能量0.276 和0.356 MeV)、最小能差为0.03 MeV(133Ba 特征能量0.356 和0.384 MeV),表明Boosted-Gold 算法反演低能量分辨率探测器γ能谱可实现较准确的分析结果,尤其具有准确的定性分析能力.

模拟γ能谱反演结果表明:最多8 种γ射线能量、γ射线强度最大比为1∶0.3、能差为1 倍FWHM条件下,Boosted-Gold 算法能够准确分析入射γ射线特征能量,γ射线反演强度与标准强度差值保持在0.01 以内;当γ射线相对强度小于10%时,反演准确性随之降低,且强度反演准确性与γ射线强度成正比,表明Boosted-Gold 算法对于相对强度大于10%的γ射线具有更好的分析准确性,但分析准确性与增强系数p取值相关,在p≤ 14 时γ放射性核素的定量分析更准确,p＞ 14 时将无法完成相对强度小于10%的γ射线的定性定量分析.由于模拟γ能谱过程更接近理想物理过程,模拟γ能谱反演结果优于实测γ能谱反演结果,说明γ能谱测量过程中误差对反演结果的准确性影响较大,γ能谱数据误差校正与反演算法结合,将进一步提升低分辨率γ能谱反演分析精度.