问题情境下建构初中数学思维型课堂的视角

吴陈悦 卜丽华

【摘要】思维型课堂指的是能够激发学生的内在学习动机，调动学生学习的积极性，使其产生强烈的求知欲，保持积极的学习情感与态度的教学课堂。在初中数学的教学过程中，教师要通过设置适当的问题情境，打磨问题的设计角度和深度，引导学生就问题展开思考、分析及探究，以促进学生思维品质与水平的提升。

【关键词】初中数学;问题情境;思维型课堂

在初中数学课堂的教学过程中，基于“相交线与垂线段”的教学内容，教师可通过创设相应的问题情境，聚焦思维品质，引导学生经历观察、猜测、归纳与建构等思维活动，实现课堂的教学目标并促进学生思维能力的提升。从这个思路出发，下面笔者围绕问题情境的引入、反问、对比、建构这几个视角展开具体探讨，真正实现以问题为驱动，建构初中数学思维型课堂。

一、引入视角，激活心理期待

引入视角指的是问题情境的引入环节。对于初中阶段的学生来讲，我们所创设的问题情境既要激活学生的心理期待，充分调动学生在课堂上的参与，也要服务于课堂的教学内容与学习任务，使得学生在思考与探究过程中能有所收获与提升。因此，教师要在引入视角的趣味性、生成性和延伸性方面多加思考，创设出有效的导入情境。

例如，以《相交线——点到直线的距离》的教学内容来讲，为了让学生理解连接直线外一点与直线上各点的所有线段中，垂线段最短。笔者在课堂引入阶段为学生创设了一个生活化的问题情境，如下图所示，“农户要想将小河L里的的水引到A处的农田里灌溉，同学们能否为农户设计一个引水方案，使得引水的路径最短呢？”这样的生活类问题一出现，学生表现出了很大的兴趣。笔者再引导学生将这样的生活情景跟课堂的知识内容对应起来。学生联想到这就是垂直线段最短在生活中的应用。那么，要想满足引水路径最短的设计要求，农田A就是直线外一点，小河L就是直线，只需要过点A作河岸的垂线段即可。这样，相关的生活情境问题还有很多，笔者顺势进行了一定的转化，问题内容不变，但河流L的流向成了西北—东南走向，继续引导学生思考及解答。就这样，学生通过结合生活情境进一步了解与巩固了垂线段的基本定理，教学效果较好。

也就是说，教师在创设问题情境式时多从生活化的视角入手，引导学生从自身熟悉的生活经历或实物中抽象出数学概念及性质，这样不仅能大大降低学习复杂知识内容的抽象性，还可以使学生意识到数学知识与实际生活的关联性，调动起学生数学学习的兴趣与积极性。

二、反问视角，引导举一反三

反问视角指的是教师可以通过“反问”，将学生在一定情境中的问题再抛回给学生，这在一定程度上可以引发学生的认知冲突，使学生能改变原有的认知图式重新建构知识与概念，以此来进一步加深学生对新知识内容的理解与巩固，促进知识点的良性迁移，提升学生举一反三的数学学习能力。

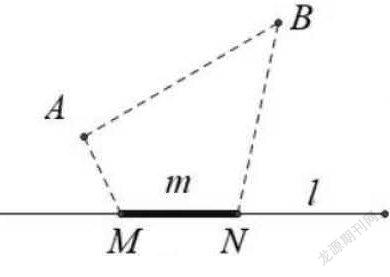
例如，在讲到相交线与垂线段的知识点时，教师可以为学生引入一个经典的问题类型：“将军饮马”求动点最值问题，这是對基础知识点在深度与难度上的延伸。笔者为学生设计的问题情境是：每天早上，将军骑马从A营地出发到河边M处饮马后，再沿着河边遛马固定的路程m到N处，然后再从N点到B营地去。问将军沿着怎样的路线遛马使得总路程最短？学生看到这个问题感到难度很大，找不到切入点。那么，笔者以反问的视角，逐步引导学生思考问题中哪些点是动点？哪些距离是固定的？学生想到两个动点是M、N，但M、N之间的距离是固定的。继续追问：那么，在M、N两点间的距离为定长的情况下，AM+MN+NB的最小值还和MN的长度有关系吗？这时，学生就能意识到只需要满足AM+BN最小即可。那么，如何满足AM、BN两点间的距离最短呢？这就可以对应到轴对称—最短路线问题的解题思路，就这样可以一步步带领学生解决解题过程中的障碍，实现复杂问题的顺利解答。

课堂是师生双方用心对话、平等交流的场所。反问策略的适当运用可以使学生与教师在课堂上建立起平等的对话关系，在交流中生成思考、生成疑问、生成矛盾，并利用更进一步的思考与探究解决矛盾、形成观点，进而有利于促使学生有效地思考、内化、巩固课堂所学知识，深化数学思维品质。

三、对比视角，发现隐性规律

对比视角是指教师可通过创设问题情境让学生比较相关知识内容的异同点，深入探究知识之间的关联性，发现隐含其中的隐形规律，并在此基础上把握知识的本质，以融会贯通的方式去学习知识，理解知识的结构，实现知识的迁移，切实提升学生深度学习的意识与能力。

例如，在教学这块知识内容时，学生会学到几个易混淆的知识点，比如，点到直线的距离与两条平行线之间的距离，以及“垂线段”与“距离”。笔者在教学时就根据对比视角，让学生利用比较异同点的方式来学习这两块知识内容。具体来讲，笔者先让学生回忆这两个基本概念，接着提问学生：点到直线能形成多少条线段？点到直线的距离形成的垂线段有几条？两条平行线之间的距离所得线段有几条？两条平行线之间的距离都相等吗？通过追问的方式让学生深入理解与剖析这两个概念的异同，把握知识点的数学本质。并以同样的方式让学生认识到垂线段是一个图形，距离是线段的长度，是一个量，它们之间不能等同。

在学习一些抽象复杂的数学知识内容时，很多学生对知识概念的理解还是停留在死记硬背的机械式记忆上，并不能深入触及和理解数学知识的本质。因此，对比设问的方式可以帮助学生以比较记忆的方式抓取教学概念中的重难点，真正达到“知其然更知其所以然”，提升初中数学课堂的教学质量。

四、建构视角，形成知识体系

知识建构强调的是学生能够从碎片化信息中建构连贯知识体系的能力，这也是教师可以创设问题情境的一个切入点。具体来讲，教师可有计划、有意识地通过设计问题引导学生将相关知识点进行整合，连点成面，不断对已有知识内容进行更深层次的迭代，促进个人知识结构的建构与完善。

例如，对于相交线的知识点而言，两直线相交所成的四个角中存在几种不同关系。那么，笔者在教学中采用了以问题为主线，将学生对知识点的回答梳理绘成表格的教学策略，以这种形式来帮助学生建构知识体系。具体来讲，笔者设置的问题包括两直线相交会形成哪四个角？是否存在公共顶点？边的关系是什么？角的关系是什么等。学生回答之后，笔者带领学生将这些知识点整理成了表格，角的类型包括对顶角、领补角，系统分析了这两类型角的基本特征，并特别指出了如果∠α与∠β是对顶角，那么一定有∠α=∠β;反之，如果∠α=∠β，那么∠α与∠β不一定是对顶角等学生易混淆的知识点，帮助学生系统梳理了关于相交线的重点知识内容。

也就是说，基于建构视角设计层层递进的问题链条，通过问题让学生展开系统思考，这样可以促使学生在思考问题、分析问题、解决问题的过程中对知识内容进行有序的梳理、归纳及总结，强化学生对知识点的建构与理解，进而促进学生深度学习的发展和核心素养的提升。

总而言之，在初中数学课堂的教学过程中通过创设合适的问题情境，启发学生思考，有利于激发学生学习的内在动力，引导学生把握数学内容的本质，具有积极的教学效用。当然，它在教学中的应用绝不仅限于文中提到的相交线与垂线段的教学内容，以及这几类教学策略，其更多的可行方式还有待教师在具体教学实践中不断进行探索与思考。

参考文献：

[1]章礼彩.串“问”为“链”，让数学问题绽放光彩——初中数学课堂中的“问题链”设置[J].中学数学研究，2020（1）：31-32.

[2]孙金瑞.初中数学问题情境的创设方式探究[J].中学数学研究（华南师范大学版），2014（9）：9-10.

[3]李荣杰.浅谈初中数学课堂问题情境的创设[J].初中数学教与学，2019（3X）：7-8.

[4]陈米华.盘活数学资源 创设问题情境——初中数学课堂教学创设问题情境的策略[J].福建教学研究，2016（2）：29-30.

责任编辑  钟春雪