分时探究：让含参函数问题更直观

陈亚楠

含参数的函数问题往往不给出图像，同学们求解时需要根据题意画出草图，“以形助数”能让探究更加直观并思维可见。下面，老师将2021年南通市中考试卷第26题适当改编后进行演示，与同学们一起深入探究其解法。

例题 定义：若一个函数图像上存在横、纵坐标相等的点，则称该点为这个函数图像的“等值点”。例如，点（1，1）是函数y=[12]x+[12]的图像的“等值点”。

若函数y=x2-2（x≥m）的图像记为W1，将其沿直线x=m翻折后的图像记为W2。试研究W1、W2兩部分组成的图像上“等值点”的个数，并指出相应m的取值范围。

这道代数类的新定义问题不难理解，横、纵坐标都相等的点在直线y=x上，函数的“等值点”就是该函数图像和直线y=x的交点。求解的难点在于直线x=m的位置不确定，导致W1、W2两部分组成的新图像发生变化，交点个数也就发生变化。

我们可以先画出函数y=x2-2和y=x的图像，通过不断地改变直线x=m的位置，直观感受W1、W2两部分组成的新图像的不同形态。不难发现，抛物线的对称轴是一个分界位置，直线x=m在其左侧或右侧都会影响新图像的形状。另外，y=x2-2和y=x图像的交点也是关键位置，它们影响新图像与y=x的交点情况。

接下来我们“分时”研究：

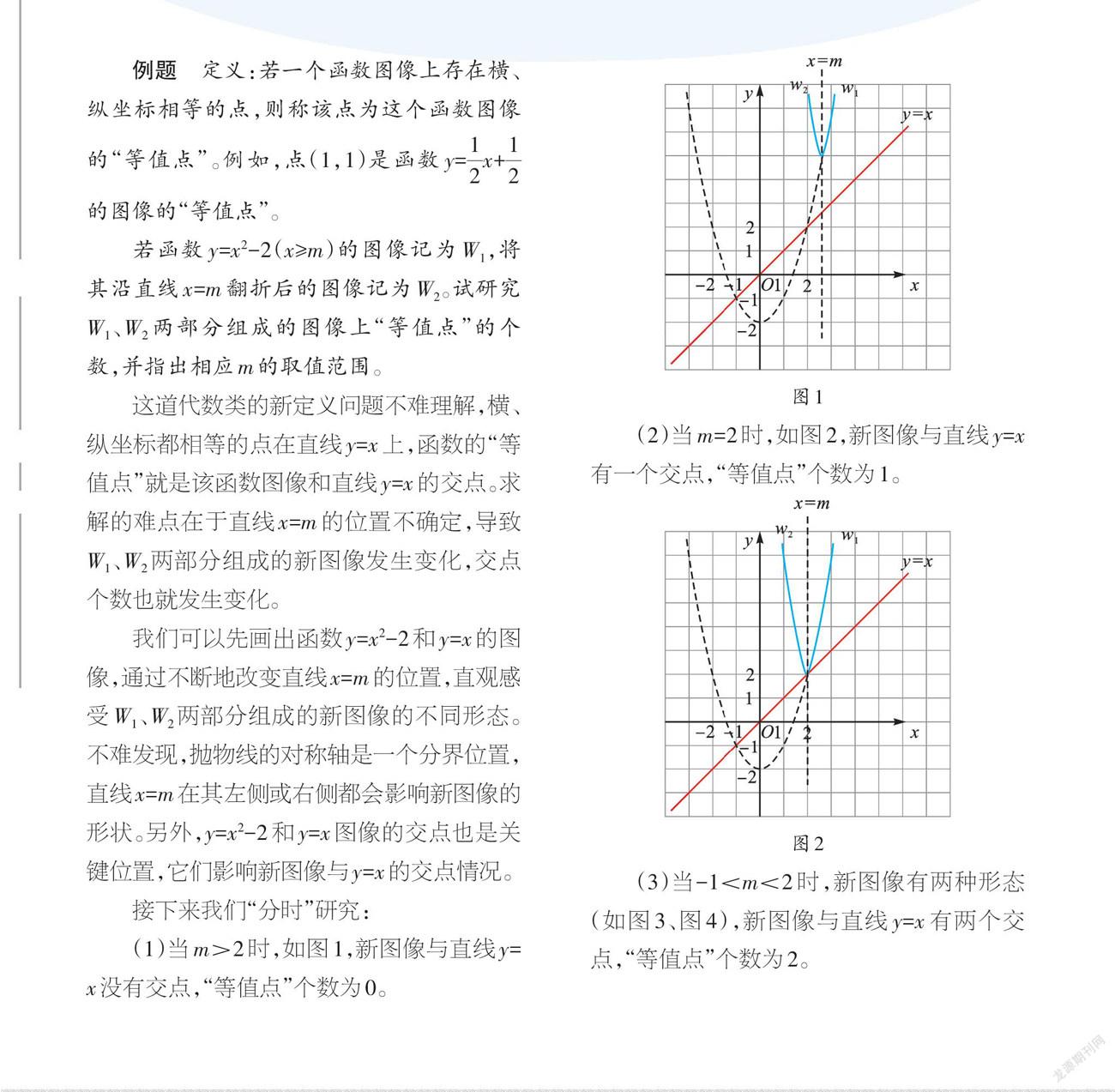
（1）当m>2时，如图1，新图像与直线y=x没有交点，“等值点”个数为0。

（2）当m=2时，如图2，新图像与直线y=x有一个交点，“等值点”个数为1。

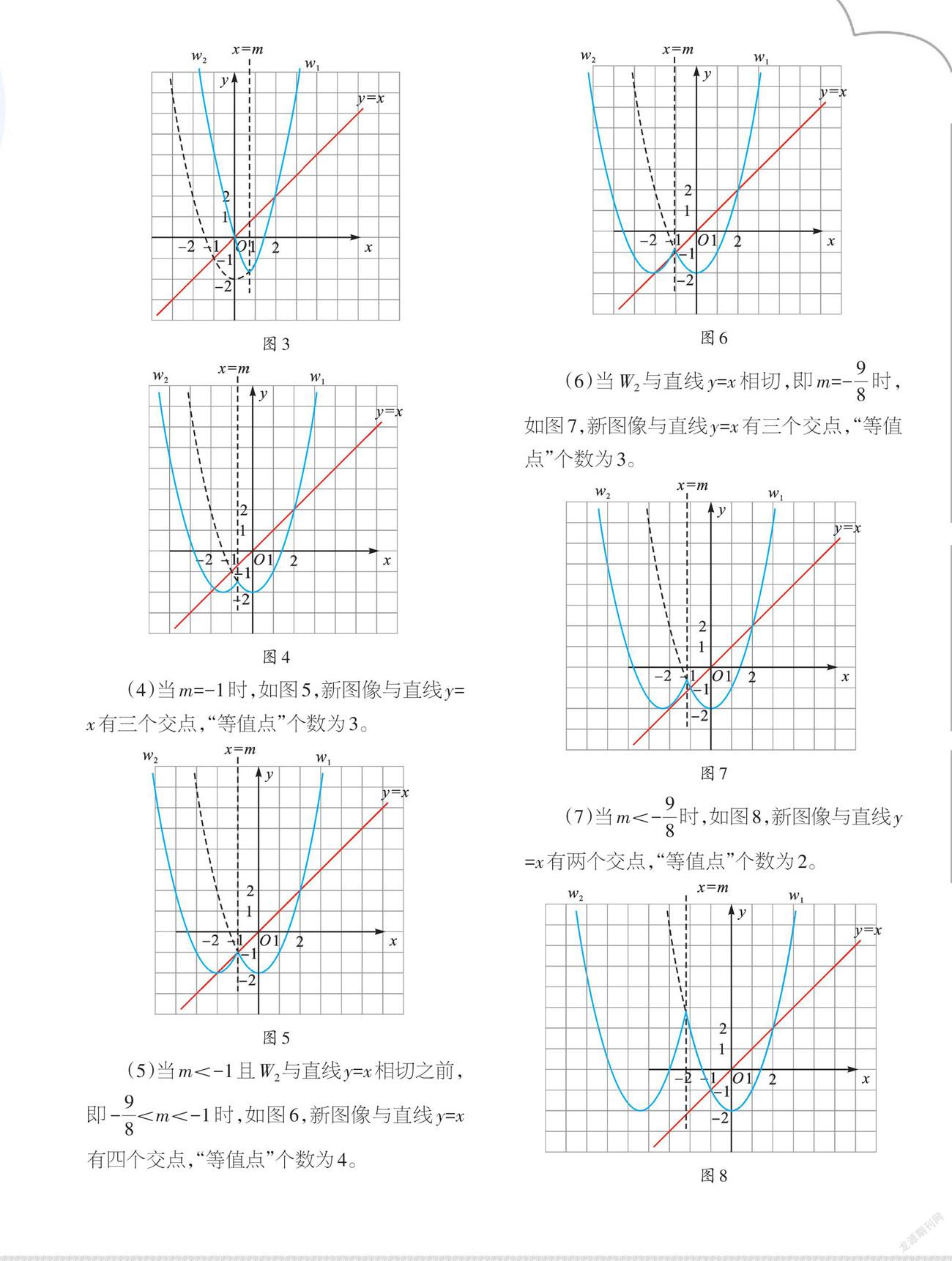
（3）当-1

（4）当m=-1时，如图5，新图像与直线y=x有三个交点，“等值点”个数为3。

（5）当m<-1且W2与直线y=x相切之前，即[-98]

（6）当W2与直线y=x相切，即m=[-98]时，如图7，新图像与直线y=x有三个交点，“等值点”个数为3。

（7）当m<[-98]时，如图8，新图像与直线y=x有两个交点，“等值点”个数为2。

最后，我们列表梳理以上情形：

[m的取值范围 “等值点”个数 m>2 0 m=2 1 -1

【小结】通过寻找临界位置，“分时”研究，我们可看清楚“等值点”变化的情况。看完本文，老师也希望同学们能体会到利用数形结合解决函数图像与直线交点问题的策略。

（作者单位：江苏省海安市城南实验中学）