高中数学教材中数学史内容对比研究的一个框架

【摘 要】 数学史是提升学生数学核心素养的重要依托，以教育目标分类学（修订版）为理论依据，从学习者的认知水平、知识分类以及数学史在教材中的主要渗透特征三个维度构建了高中数学教材中数学史内容对比研究的框架. 基于本框架对新人教A版高中数学必修册和北师版高中数学必修册教材中数学史的相关内容进行了对比研究. 结果显示：二者在总体数量方面相差不大;在认知水平和知识分类两个维度的史实分布特征具有较强的一致性;在主要渗透特征方面二者呈现出一定的差异性. 为教师教学提出以下几点建议：（1）引导学生以史料为背景进行数学写作，提高学生数学元认知水平;（2）前置“数学史学习任务清单”，以兴趣引领学生主动认知;（3）史实材料的选取要兼顾“德育”和“智育”，培养学生数学核心素养.

【关键词】 数学史;高中数学;教材对比

1 问题提出

随着数学课程改革的不断深入，数学文化的育人价值被逐渐挖掘. 2003年，我国首次将数学文化纳入普通高中数学课程标准[1]，这意味着数学文化已经受到数学教育界的广泛关注. 数学史作为数学文化的有机组成部分，是學生了解数学科学发展脉络、体会数学文化属性的重要依托，而教科书作为教师“教”与学生“学”的主要载体，是开展数学史实学习的重要资源. 2019年，我国部分地区开始率先使用依据《普通高中数学课程标准（2017版）》编写的新版高中数学教材，按照教育部“同纲异构”的教材编写原则，各版本教材在数学史内容的选择和编排上存在着一定的差异.

对数学史在各版本教材中的选择和编排进行研究，不仅有利于总结教材编写经验，为今后的教材编写提供借鉴，而且对于教师把握教材、体会教育理念的转变有着重要的指导意义. 通过对文献进行研读，笔者发现已进行的数学史对比研究多从数学史在教科书中的内容类型、内容来源、呈现视角等方面进行探索和比较[2][3][4]，而从学习者的认知水平和知识分类这两个角度的研讨较少. 本研究从数学史在教科书中的主要渗透特征、学生对数学史的认知水平以及知识分类三个维度构建了高中数学教材中数学史内容对比研究的框架，以期为广大数学教育工作者提供参考，对不同版本高中数学教材进行广泛对比研究，为教师的史实教学提供建设性意见. 2 三维框架构建

2.1 理论依据

《布卢姆教育目标分类学（修订版）分类学视野下的学与教及其测评》[5]（以下简称《修订版》）是对Lorin W.Anderson和David R.Krathwohl等人所编写的《教育目标分类学：认知领域》一书的修订和完善. 《修订版》将原认知框架修改为知识和认知过程两个维度，知识维度划分为事实性、概念性、程序性、元认知知识四个类别;认知过程划分为记忆/回忆、理解、应用、分析、评价、创造六个类别，每一类别又划分为2～7个不等的亚类共30个. 应该说《修订版》作为当今完善程度最高、适用范围最广的教育目标分类理论之一，为教育科研人员提供了良好的理论研究框架，同时也为一线教师的教学实践提供了操作指引和理论支撑;但高中数学教材中的数学史内容有限、涉及范围较窄，过细的类别划分对于《修订版》在数学史领域的应用是十分困难的. 布卢姆曾提出：“每个领域都应该有符合该领域实际特征的目标分类系统，它更详细，更接近于该领域的语言符号系统和问题思维方式，因此，在合适的情况下，它可以具有新的类别及类别的合并与删除.”因此，将原分类系统进行整合与删除后，其在数学史领域的可操作性可能会更强. 2.2 框架建构2.2.1 从学习者认知水平的角度

1.了解与记忆史实

对于数学教科书中出现的具有如下特征的数学史实内容了解和记忆即可： 无需通过任何形式和手段（如通过查阅资料对其进行归纳、总结与拓展）对史实材料进行加工，仅以阅读的形式进行认知;不涉及数学技能和数学思想方法的运用. 一般来讲，数学名言、数学家简介和数学符号的由来等史料都属于这一层次.

2.理解与应用史实

对于数学教科书中出现的具有如下特征的数学史实内容需要进行理解和应用：在认知过程中涉及到运算、推理、画图、数据整理等解决数学问题所必需的数学技能的史实材料;以史实材料（即包括数学自身发展历史，也包含数学在其他学科中的应用史）为背景的数学建模活动. 例如新人教A版高中数学教科书必修第一册P39探究中第24届国际数学家大会会标的由来——赵爽弦图，见图1. 虽然学习者在初中已经学习过赵爽弦图的相关史实内容，但由于此处要求从图中“找出一些相等关系和不等关系”，故此处史实内容从认知水平来看要达到理解与应用的层次.

新人教A版教材P39探究活动

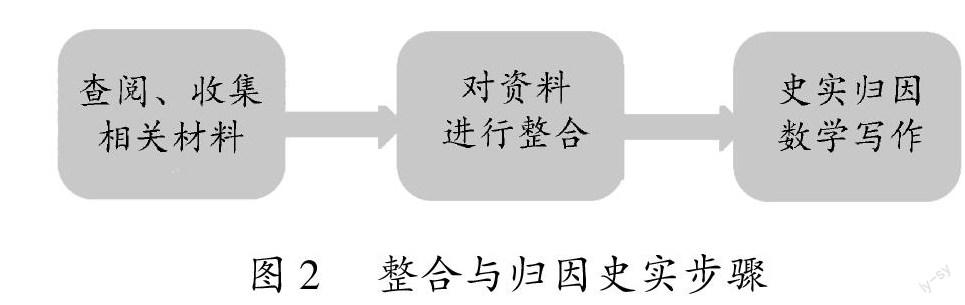
3.整合与归因史实

对于数学教科书中出现的具有如下特征的数学史实内容需要进行整合与归因：需根据已有的史实材料、通过查阅资料等手段对其进行分析、拓展和评价，并最终以数学写作的形式进行汇报的任务.

例如新人教A版选择性必修第一册P89中的“请你查阅有关资料，进一步了解吴文俊的事迹，了解我国数学家在数学机械化方面的卓越贡献”. 要想完成上述学习任务，学习者可以按照如下步骤进行，见图2.

2.2.2 从知识分类的角度1.陈述性史实知识

将数学教科书中出现的具有如下特征的数学史实内容划分为陈述性史实知识：史实内容为数学发展所必须的基本要素：关于语言的或计算的符号、历史事件的地点、人物及其言论等史实;上述基本要素的文字扩展、评价，不同要素间的以文字为主要形式的整合. 例如人教A版高中数学教科书必修第一册P62旁注，“函数符号y=f（x）是由德国数学家莱布尼茨在18世纪引入的”就是一个陈述性史实知识;人教A版高中数学教科书必修第一册P97，以“函数的形成与发展”为主题进行文献阅读和数学写作，这是众多数学基本要素间的整合，属于陈述性史实知识.

2.应用性史实知识

将数学教科书中出现的具有如下特征的数学史实内容划分为应用性史实知识：与数学定理、数学思想方法、数学技能有关的史实内容;以史实（既包括数学科学自身发展历史，也包含数学在其他学科中的应用史）为背景建立数学模型的相关知识. 例如新人教A版必修第二册P81中的“代数基本定理”;P91中的“棣莫佛定理”;P121中的“祖暅原理”等都属于应用性史实知识. 2.2.3 从主要渗透特征的角度1.总体数量：即数学史在数学教材中的出现次数.

2.运用方式：汪晓勤提出了数学教材运用数学史的五种方式[6]，具体内容见表1.

3.呈现位置：数学史在数学教材中的呈现位置主要有三种：前置式、并置式和后置式[3]. 前置式即指数学史出现在数学知识之前，并置式即数学史与数学知识同时出现，后置式是数学史在数学知识之后出现. 例如：北师版高中数学教材每一章都以数学名言引入，这是前置式;人教A版教材在介绍弧度制时，在旁注介绍了弧度制概念的提出，这就是并置式. 三维对比研究框架整体结构见图3.

3 案例分析3.1 研究对象

以新人教A版高中数学必修册教材和北师版高中数学必修册教材为对象进行对比研究. 将数学史的概念界定为：数学教科书中涉及到的有关数学概念、定理、思想方法的发展历程，数学家简介、与数学有关的名言，数学符号的由来，数学在社会政治、经济、文化以及其他领域的应用史. 3.2 研究结果分析3.2.1 二者在认知水平维度和知识分类维度的史实分布特征具有较强的一致性研究发现，新人教A版必修册和北师版必修册在认知水平和知识分类两个维度的史实分布特征具有较强的一致性，即P1、P2层次的史实内容相比较多，P3层次較少，K1、K2两个层次的史实内容数量较接近，且K2层次的史实内容略多于K1层次，见图4. 具体来说，新人教A版必修册在P1、P2、P3层次的史实数量分别为15处、22处和5处，在K1、K2层次的史实数量分别为18处和22处;北师版必修册在P1、P2、P3层次的史实数量分别为20处、25处和4处，在K1、K2层次的史实数量分别为21处和28处.

3.2.2 二者在数学史的运用方式及呈现位置方面具有一定的差异性

在主要渗透特征方面，二者呈现出“一同二异”的表现特征. 具体而言，在总体数量方面，新人教A版和北师版必修册相差不大，分别为42处和49处;在运用方式方面，新人教A版教材在点缀式、附加式、复制式、顺应式、重构式这五种方式的占比分别为0%、47.6%、2.4%、28.6%、21.4%，而北师版的这一数据为0%、20.4%、24.5%、49.0%、6.1%;在呈现位置方面，新人教A版中数学史内容在前置式、并置式、后置式这三个位置的占比分别约为4.8%、57.1%、38.1%，而北师版的这一数据为28.6%、16.3%、55.1%，究其原因是北师版教材中引用了大量的数学名言放置在章首页，这就造成了北师版“前置式”和“复制式”在各自整体内占比较高，见图5.

3.2.3 从三维结构整体来看，二者各具特色

从三维结构整体来看，二者各具特色，既有共同关注的重点，也有不同的渗透理念，见表2. 首先，二者对学生在陈述性史实知识方面的认知水平要求较低，多为P1层次，分别为14处和17处，而对于应用性史实知识的认知水平要求多为P2层次，分别为22处和23处. 其次，二者都是处于（P2，C2，K2）层次的史实内容最多，且这一层次史实内容的渗透特征也较相似，即都是顺应式运用最多、附加式次之. 但是，北师版在这一层次共运用顺应式20次，占比87.0%，而新人教A版在这一层次的主要运用方式也为顺应式，但占比只有54.5%，可见，北师版教材的编写侧重于对史实内容的加工，而新人教A版还关注史实的重构. 此外，二者在（P3，C3，K1）和（P3，C3，K2）层次、（P1，C3，K1）和（P2，C3，K2）层次的呈现位置方面也呈现出了较强的一致性. 由此可见，在整体结构方面，二者各有所长，既有共性，也有差异.

4 启示

教材作为贯彻课程标准和承载课程理念的物质载体，是师生开展史实学习的重要资源. 通过对框架的构建和两个版本教材中数学史内容的对比研究，发现了两个版本教材在数学史内容的选择和编排上的共性与差异，为教师教学提出以下三条建议. 4.1 引导学生以史料为背景进行数学写作，提高学生数学元认知水平

研究表明，数学写作可以有效提高学生的数学元认知水平[7]，而对史实内容进行整合与归因，就是学习者通过收集、归纳、整理等方式，从更高的视角对史料进行意义建构，并最终以数学写作的形式呈现的过程. 这一过程不仅有利于学习者了解数学概念、公式、定理的发生发展脉络，更重要的是对于学生数学元认知水平的提升具有重要意义. 在新人教A版教材和北师版教材中，P3层次的史实数量占比分别为12%和8%，相比P1、P2层次的史实数量占比较低. 因此，在教学过程中，教师要有意识地引导学生对教材中涉及的史料进行拓展与分析，培养学生收集、分析、归纳材料和数学写作方面的能力，提升学生的数学元认知水平. 4.2 前置“数学史学习任务清单”，以兴趣引领学生主动认知

美国数学家魏尔德认为：数学课堂上只强调数学的技术是不够的，要使学生被数学所吸引，一定要运用数学历史知识[8]. 而史料的不同运用方式和呈现位置会给学生带来不同的情感体验. 在运用方式方面，教师要借鉴教材，采取顺应式和重构式的方式，以此来保证史料的时代适用性. 在史料呈现位置方面，教师可以在章开头设置“数学史学习任务清单”. 例如“圆锥曲线的方程”这一章涉及了大量的史实知识，从梅内赫莫斯的“梅氏三线”到欧几里得的《圆锥曲线》，再到阿波罗尼奥斯的《圆锥曲线论》和安提缪斯的“两钉一线”椭圆画法[9]，学生只有了解圆锥曲线的产生发展历程，对知识的建构才会更加深刻. 在学习本章之前，教师可以预先列出每一节涉及的史料，引导学生自主探索，调查圆锥曲线的发展历程，激发学生的学习兴趣，促进学生主动认知. 4.3 史实材料的选取要兼顾“德育”和“智育”，培养学生数学核心素养数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度和价值观的综合体现[10]，即核心素养的培养要兼顾“德育”和“智育”. 数学史在数学与人文之间架起了一座桥梁，因而在德育上可以发挥独特的优势[9]. 因此，教师在史料的选取过程中，在保证趣味性、科学性、可学性、有效性、人文性的史料选取原则下[11]，要重视中国传统文化中的数学元素，兼顾学生的德与智共同发展. 例如，在介绍《赵爽弦图》的过程中，也可以将赵爽“负薪余日，聊观《周髀》”的故事介绍给学生，这样既让学生了解了赵爽弦图，发展了学生的“智”，又让学生感受到赵爽刻苦钻研的精神，培养了学生的“德”.

参考文献

[1] 史宁中，吕世虎，李淑文.改革开放四十年来中国中学数学课程发展的历程及特点分析[J].数学教育学报，2021，30（01）：1-11.

[2] 刘云，朱维宗.高中数学必修教科书中数学史内容的呈现方式探析[J].数学教育学报，2012，21（02）：86-89.

[3] 徐乃楠，孔凡哲，刘鹏飞.高中数学教科书中的数学史呈现研究[J].数学教育学报，2015，24（02）：61-65.

[4] 张盛熔.新人教A版高中数学必修册教科书中数学史内容的研究[D].武汉：华中师范大学，2020.

[5] Lorin W.Anderson等.布卢姆教育目标分类学修订版：分类学视野下的学与教及其测评[M].蒋小平等译.北京：外语教学与研究出版社，2009，21-48.

[6] 蒲淑萍，汪晓勤.数学史怎样融入数学教材：以中、法初中数学教材为例[J].课程·教材·教法，2012，32（08）：63-68.

[7] 胡耀华.数学写作的价值及若干教学建议[J].数学教育学报，2007，56（03）：60-62.

[8] 杨渭清.数学史在数学教育中的教育价值[J].数学教育学报，2009，18（04）：31-33.

[9] 汪晓勤，沈中宇.数学史与高中数学教学——理论、实践与案例[M].上海：华东师范大学出版社，2020：60.

[10] 中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018：4.

[11] 陈晏蓉，汪晓勤.数学史料的选取原则与案例分析[J].教育研究与评论（中学教育教学），2017（12）：37-43.

作者简介 常海斌（1999—），男，吉林公主岭人，硕士生;主要从事数学教育研究.