以操作助理解

程广

十进位值制记数法包括“十进制”与“位值制”两条原则。这种记数法的本质特征是省略记数单位，可以给多位数的认识和计算带来根本性的改进。日常教学中，如何帮助学生更好地理解十进位值制记数法及其价值？如何运用位值制思想帮助学生更好地认识大数，实现算理、算法的深度理解？本期我们来讨论上述问题。

“位值”是一个抽象的概念。能否深刻理解位值制的基本意义，并在此基础上建构位值模型，直接影响学生对数的整体认识和对数的运算原理的理解。笔者结合北师大版数学教材，谈一谈如何引导学生整体建构十进位值制。

一、借助实物操作，初步建构位值概念

教师提供可操作的实物辅助学生认识数，对于学生理解数的概念十分必要。在教学《古人计数》（11～20的认识）时，笔者让学生经历了由借助小棒数数到借助计数器数数的过程，使学生在动手操作中感知位值制，建立初步的位值模型。

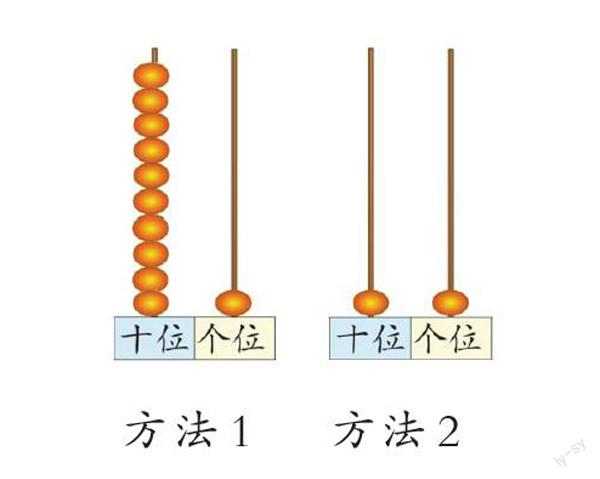
课堂上，笔者首先利用课件播放从羊圈里放出11只羊的情景，引导学生摆出11根小棒，并要求学生尽量让人一眼就能看出摆了多少根。实践中，有的学生在左边均匀地摆出10根，在右边再摆1根;有的学生摆出两组5根，再加1根;还有的学生把10根聚成一堆或捆成一捆，旁边再摆1根。笔者一一展示后提问：你觉得哪种摆法能让人一眼看出是11根？学生回答：把10根捆成一捆、再额外摆1根的方法最容易看出是11根。笔者小结：小棒没有被捆起来的时候表示10个一，“10个一”捆成1捆后就变成了“1个十”，也就是说，10个一即1个十。接着，笔者让学生动手操作，将手中的小棒数一数、捆一捆、摆一摆，再和同桌交流摆小棒的过程。在捆、说的过程中，学生充分认知到10个一是1个十。然后，笔者引导学生用计数器表征11。学生呈现以下两种方法（如下图）。笔者追问：这两种拨法，你觉得哪一种是对的？一名学生回答：我觉得方法1是对的，左边有10颗珠子，右边有1颗珠子，合起来是11颗珠子。另一名学生反驳：我觉得方法2是对的，因为计数器上写着“个位”和“十位”，个位上的1颗珠子代表1个一，十位上用1颗珠子就能代表1个十，而不是用10颗珠子。笔者小结：计数器十位上的1颗珠子表示1个十，相当于1捆小棒;个位上的1颗珠子表示1个一，相当于1根小棒。最后，笔者提问：计数器中，同样是1颗珠子，在不同的数位上表示的意义一样吗？学生回答：不一样，十位上的1颗珠子表示1个十，个位上的1颗珠子表示1个一。学生明白了数的位置不同，其意义也不同的道理。

10及10以内数的学习，学生是运用“一一对应”的思想逐一计数的，但到了20及20以内数的认识，学生开始由逐一计数过渡到按群计数。教师让学生通过直观操作理解“10个一就是1个十”，使学生将1捆小棒与计数器十位上的1颗珠子对应起来，初步体会位值的含义。

二、由具体到抽象，深化理解位值概念

有了认识20以内数的学习基础，在教学100以内数的认识时，笔者让学生再次进行直观操作——拨一拨计数器，旨在深化学生对位值制的理解。

教材通过“数豆子”的活动引导学生先拨出28、22等数，再让学生拨出99。如何拨出99呢？学生提出先在十位上拨9颗珠子表示9个十，再在个位上拨9颗珠子表示9个一，合起来就是99。笔者追问：两个“9”的意思一样吗？学生分析：十位上的9表示9个十，个位上的9表示9个一，两个“9”表示的意思不同。笔者追问：如果再增加1个，该怎样拨？学生不加思索地回答：在个位上再拨1颗珠子。笔者按照学生说的拨出来，并提问：你们有什么发现？学生思考后回答：个位上再拨1颗后，就有了10个一，10个一是1个十，就要将个位上的10颗珠子拨走，换成十位上的1颗珠子。笔者根据学生说的进行操作后追问：你们还有什么发现吗？学生马上发现十位上添上1颗珠子（1个十）后，它与原本的9个十合成了10个十，10个十就是1个百，又要将十位上的10颗珠子拨走，换成百位上的1颗珠子。学生在拨99再加1的过程中弄清了“10个十是100”，进一步体会到“同一个数字在不同的数位上表示的意义不同”，深化了对计数单位及“十进”关系的理解。

后续教学中，笔者给学生布置了两道思考题。第一道题是给出两颗珠子，问学生可以表示哪些数。学生马上想到可以表示11。笔者追问这两颗珠子放在哪里、表示什么。学生回答“1颗珠子放在十位上，表示1个十，另1颗珠子放在个位上，表示1个一，合起来是11”。笔者提示：这两颗珠子只能这样放吗？一名学生说：可以将这两颗珠子都放在个位上，表示2个一，就是2。另一名学生说：可以将这两颗珠子都放在十位上，表示2个十，即20。第二道题是给出5颗珠子，问学生可以表示哪些数。学生有了解决上一题的经验，分别说出可以表示5、14、23、32、41、50这些数，并说出了每个数位上的数字所表示的意思，内化了位值概念。

三、由简及繁，整体建构十进位值制

学生有了上述学习基础，教师在教学“万以及万以内数的认识”时，就可以直接用多媒体呈现计数器、小方块的图像，用抽象的学具引导学生学习新的数位，进而认识十进制数位顺序表，整理出由一（个）、十、百、千、万、十万、百万等计数单位组成的计数系统。

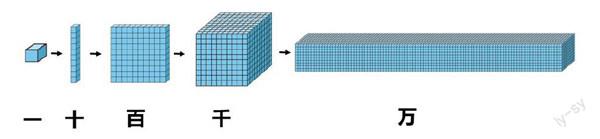
课堂上，笔者借助多媒体一边引导学生快速、有序地数出小方块的个数，一边动态呈现一（个）、十、百、千、万等计数单位的形成过程（如下图）。学生在多次有序数数的过程中，自然而然地明白了10個一是十、10个十是一百、10个一百是一千、10个一千是一万，进一步体会到计数单位之间的十进关系。

在教学更大的数时，笔者借助多媒体呈现计数器，让学生跟随拨珠子的动态过程一万一万地数数。学生数到九万时，笔者追问：九万之后再数一万是多少？有的学生说是十万，有的学生说是一亿。笔者引导：万位上的9颗珠子表示9个一万，9个一万再加一万就是10个一万，10个一万是十万，不是一亿。通过这样的引导，笔者自然地引出计数单位“十万”，并指出计数器上十万位的位置。接下来，笔者引导学生运用类比迁移法找出百万位、千万位、亿位、十亿位、百亿位、千亿位，并与学生一起整理、完善了十进制数位顺序表。学生在操作、分析、整理的过程中将数级从个级扩充到万级、亿级，提升了数感。

这样设计教学，旨在让学生经历从直观到抽象的思维过程，利用知识内在的联系整合教学内容，使前后所学知识呈现出整体性、系统性、结构性，帮助学生实现知识的深层加工、深刻理解，以及长久记忆，达成深度学习。

责任编辑  刘佳