从一个定理的引入方式多视角理解数学教材

刘向权

【摘 要】  “直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质定理.本文通过对初中数学教材现行的十个版本的比较分析，简要归纳这一定理几种不同的引入方式，进而尝试从多视角分析、理解数学教材，以期为广大教师在教学中准确把握教材编写思路、恰当处理有效利用教材提供参考.

【关键词】  教材编写;定理引入;多视角;教材理解

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）对第四学段（7～9年级）的课程内容有如下规定：理解直角三角形的概念，探索并掌握直角三角形的性质定理：直角三角形的两个锐角互余，直角三角形斜边上的中线等于斜边的一半[1].对于“直角三角形的两个锐角互余”这一性质定理，在学生理解直角三角形概念的基础上，结合三角形内角和定理即可顺理成章地推导出;而对另一个性质定理——直角三角形斜边上的中线等于斜边的一半，何时引入，如何呈现，新课标并未给出明确建议或说明.今年暑期，在沪科版八年级下册数学新教材审读视频讨论会上，有编写人员提及与此定理的引入方式有关的话题，不禁引起了笔者的深思，进而促使笔者对初中现行十个版本的数学教材进行比较分析.本文通过系统梳理、简要归纳此定理几种不同的引入方式，尝试从思维生长、知识系统和“特殊关联”三个视角分析、理解数学教材，以求抛砖引玉.  1  定理引入方式梳理呈现

1.1 由“矩形的对角线相等”引入

在初中现行十个版本的数学教材中，以下五个版本均采用了这一引入方式.

1.1.1 沪科版教材八年级下册第19章第3节第1小节“矩形”

在得出“矩形的对角线相等”这一定理后，教材作了如下表述：对于任一个直角三角形 ABC（其中∠ABC=90°），构造一个长为AB和宽为BC的矩形ABCD（如图1）.设矩形对角线AC和BD相交于点O，则AO=OC=BO=OD= 1 2 AC= 1 2 BD.由此，得到直角三角形的一个性质：直角三角形斜边上的中线等于斜边的一半[2].

1.1.2 青岛版教材八年级下册第6章第3节“特殊的平行四边形”

教材在证得“矩形的对角线相等”后，设计了如下问题串：如图2，矩形ABCD的两条对角线交于点O，沿对角线AC将矩形剪开，得到 Rt △ABC.这时，OB是这个直角三角形的一条什么线段？它与斜边AC之间有怎样的数量关系？由此你发现了直角三角形的一个怎样的性质？能证明你得到的命题是真命题吗[3]？

教材再将 Rt △ABC按如图3所示的方式构造成矩形ABCD，证明命题，得到定理.

1.1.3 人教版教材八年级下册第18章第2节第1小节“矩形”

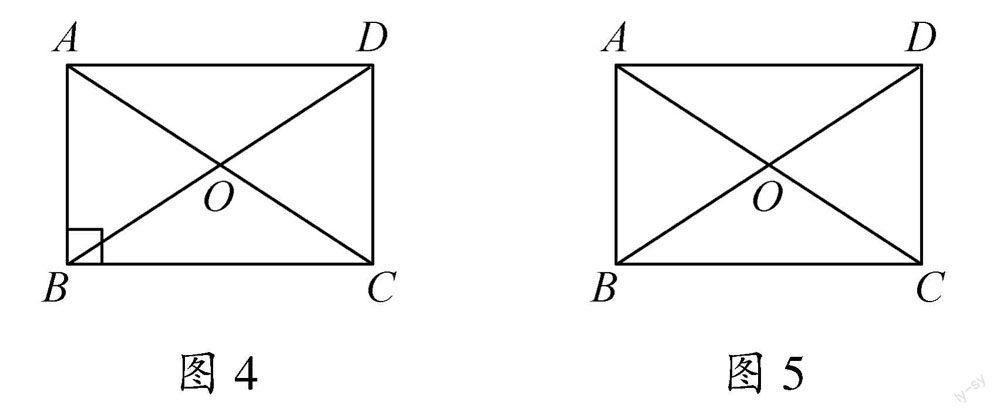
在归纳得到矩形的性质定理（矩形的对角线相等）后，教材呈现了如下“思考”：如图4，矩形ABCD的对角线AC，BD相交于点O.我们观察 Rt △ABC，在 Rt △ABC中，BO是斜边AC上的中线，BO与AC有什么关系[4]？

1.1.4 北京版教材八年级下册第15章第4节第1小节“特殊的平行四边形的性质”

教材在归纳得到“矩形的对角线相等”的基础上，安排了如下例题：如图5，在矩形ABCD中，两条对角线AC，BD相交于点O，AB=OA=4 cm .求BD与AD的长[5] .

待例题求解完毕，教材顺势引导学生作如下“交流”：

1.如图5，矩形ABCD的对角线AC与BD相交于点O，那么BO是 Rt △ABC中一条怎样的特殊线段？它与AC有怎样的大小关系？为什么有这样的大小关系？

2.在这里，我们可以从矩形对角线的性质得到关于直角三角形的一个性质，应当怎样叙述这个性质[5]？

1.1.5 北师大版教材九年级上册第1章第2节“矩形的性质与判定”

在推导出“矩形的对角线相等”這个定理后，教材设置了“议一议”：如图6，矩形ABCD的对角线AC与BD交于点E，那么BE是 Rt △ABC中一条怎样的特殊线段？它与AC有什么大小关系？由此你能得到怎样的结论[6]？

1.2 由直角三角形的其他性质引入

在初中现行十个版本的数学教材中，以下四个版本采取了这一引入方式.

1.2.1 湘教版教材八年级下册第1章第1节“直角三角形的性质和判定（Ⅰ）”

教材通过简要推理得到直角三角形的性质定理（直角三角形的两个锐角互余）及其逆定理，接着安排了如下“探究”：如图7，画一个 Rt △ABC，并作出斜边AB上的中线CD，比较线段CD与线段AB之间的数量关系，你能得出什么结论[7]？

1.2.2 冀教版教材八年级上册第17章第2节“直角三角形”

在归纳得到“直角三角形的两个锐角互余”这一定理及其逆定理后，教材进一步引导学生“观察与思考”：在一张半透明的纸上画出 Rt △ABC，∠C=90°，如图8（1）;将∠B折叠，使点B与点C重合，折痕为EF，沿BE画出虚线CE，如图8（2）;将纸展开，得到图8（3）.

（1）∠ECF与∠B有怎样的关系？线段EC与线段EB有怎样的关系？

（2）由发现的上述关系以及∠A+∠B=∠ACB，∠ACE+∠ECF=∠ACB，你能判断∠ACE与∠A的大小关系吗？线段AE与线段CE呢？从而你发现了什么结论[8]？

1.2.3 浙教版教材八年级上册第2章第6节“直角三角形”

教材在简要推导出“直角三角形的两个锐角互余”这一性质后，设置了如下“做一做”：

1.已知直角三角形两个锐角的度数之比为3 ∶ 2，求这两个锐角的度数.

2.已知：如图9，D是 Rt △ABC斜边AB上的一点，BD=CD.求证：AD=CD.

从本题中，你发现直角三角形斜边上的中线有什么性质[9]？

1.2.4 华东师大版教材九年级上册第24章第2节“直角三角形的性质”

教材在引导学生回顾之前所学的“直角三角形的两个锐角互余”和勾股定理的基础上，为继续探索直角三角形的其他性质，进而引导学生作如下“探索”：如图10，画 Rt △ABC，并画出斜边AB上的中线CD，量一量，看看CD与AB有什么关系[10].

1.3 由“等腰三角形的轴对称性”引入

在初中现行十个版本的数学教材中，唯有苏科版教材“独辟蹊径”，采取了与其他版本数学教材迥异的引入方式.

（八年级上册第2章第5节“等腰三角形的轴对称性”）在学完等腰三角形的性质和判定后，安排了如下“操作”：

剪一张直角三角形纸片，如图11（1）.

把纸片按图11（2）所示的方法折叠，再把纸片展平后按图11（3）所示的方法折叠，你有什么发现[11]？

2  由定理的不同引入方式多视角理解数学教材

2.1 基于思维生长的视角

思维生长和发展是一种极其复杂的现象.一般地，具备了一定条件时思维才能得以生长，思维发展才能得以实现.这里所说的条件，是满足思维生长、发展的动力条件[12].从“矩形的对角线相等”引入对“直角三角形斜边上的中线等于斜边的一半”这一定理的探究，恰恰可以帮助我们从思维生长的视角理解数学教材.那么，引发和推动学生思维生长、发展的动力又从何而来呢？

前文所述前五个版本的初中数学教材，虽然都是由“矩形的对角线相等”引入“直角三角形斜边上的中线等于斜边的一半”这一定理，但引入的基本思路或者说思维生长、发展的具体方向却不尽相同.沪科版和青岛版教材强调用直角三角形“构造”矩形，而人教版、北京版和北师大版教材则倾向于从“矩形的对角线相等”直接过渡得到“直角三角形斜边上的中线等于斜边的一半”.然而，在实际教学中，这两种处理方式都面临着如何才能让学生“想得到”的问题.

对于第一种处理方式（沪科版和青岛版教材），笔者认为，可依次提出如下问题来逐步引导、推动学生的思维生长、发展过程：由本节课所学的矩形，你最容易联想到哪一类特殊三角形（直角三角形 ）？现有一个矩形，你如何才能把它分成两个完全一样（全等）的直角三角形？反过来，如果给你一个直角三角形，用什么方法才能“构造”出矩形？你是如何想到这样“构造”的？怎样证明你所“构造”的四边形是矩形？观察、分析由直角三角形“构造”矩形的过程，结合“矩形的对角线相等”这一定理思考：直角三角形斜边上的中线与斜边之间存在什么关系？

相比之下，第二种处理方式（人教版、北京版和北师大版教材）显得较为直接，甚至有些“突兀”， 尤其是人教版教材的处理方式简洁明快，颇有“快刀斩乱麻”之感. 这种相对简捷的处理方式固然可以让数学结论“来得更快些”，但教师若不注重对教材的“加工”“改造”，便极易挤压学生的思维空间.笔者发现，在学习“直角三角形斜边上的中线等于斜边的一半”这一定理之前，人教版、北京版和北师大版教材均已学过“勾股定理”，学生利用“面积法”，对用外弦图（图12）和图13证明勾股定理已比较熟悉.鉴于此，教师不妨结合如下问题加以引导，通过搭“脚手架”的方式促进学生的思维生长：由这节课所学的矩形，你最容易联想到哪一类特殊的三角形（直角三角形 ）？你还记得与直角三角形的三边有关的一个重要定理吗（勾股定理 ）？你能分别用图12和图13证明勾股定理吗？根据从图12到图13的“演变”过程，你觉得图14可以“演变”成一个什么样的图形（图 15）？结合图14和图15，你发现直角三角形斜边上的中线与斜边之间有什么关系？

学生通过观察这四个图形不难发现，将图12沿虚线剪去“一半”便可得到图13.只要教师引导方法得当，学生便很容易将这一经验迁移到从图14到图15的“演变”中，因为将图14沿AC剪去“一半”恰好也能得到图15.这样的图形“演变”是多么神奇，多么美妙，又是多么相似！

2.2 基于知识系统的视角

对数学学科而言，尤其“应该从系统的角度学习知识，置知识于系统中，着眼于知识之间的联系和规律，从而深入本质”[13].基于这一观点，教师“在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系”[1].

如前文所述，湘教版、冀教版、浙教版、华东师大版教材对“直角三角形斜边上的中线等于斜边的一半”这一定理的引入，均以直角三角形的其他性质为起点.若继续翻阅这四个版本的教材还会发现，湘教版教材八年级下册第1章第1～2节已涵盖了直角三角形性质与判定的全部内容，本章第3节索性将直角三角形全等的判定（HL）也纳入了“直角三角形”的知识系统中;冀教版教材则将“直角三角形”和“等腰三角形”一起融入了八年级上册第17章“特殊三角形”這个更大的知识系统，全章涉及“直角三角形”的部分自然也少不了直角三角形的性质、判定及“HL”定理等内容;浙教版教材仿佛是在织一张更大的“网”，八年级上册第2章（特殊三角形）以“图形的轴对称”为引子，以“特殊三角形”为明线，以“逆命题和逆定理”为暗线，不仅将“等腰三角形的性质与判定”“直角三角形的性质与判定”两个子系统纳入其中，线段垂直平分线性质定理的逆定理、角平分线性质定理的逆定理也被一网打尽;华东师大版教材九年级上册第24章（解直角三角形）第2节（直角三角形的性质）在对“直角三角形斜边上的中线等于斜边的一半”进行探索前，首先回顾了前面（八年级上册第13章，第14章）学过的直角三角形的两个性质，其意图本已不言自明，而接下来探索证明得到“直角三角形斜边上的中线等于斜边的一半”这个新的性质定理后，教材依次对直角三角形的三个性质编上了序号，这个看似微不足道的细节处理，无疑更彰显出教材试图构建结构化的数学知识体系的深刻用意.

2.3 基于“特殊关联”的视角

初中数学教材中某些特殊的几何图形时常“相伴而生”，彼此能通过相互“演变”而得到，此时，往往可由其中一个几何图形的性质或判定推出另一个几何图形的性质或判定，我们不妨称这两个几何图形“特殊关联”.显然，直角三角形和等腰三角形就是这样的“特殊关联”.前文提及苏科版教材八年级上册第2章第5节利用“等腰三角形的轴对称性”探索、证明“直角三角形斜边上的中线等于斜边的一半”，就是一个很好的例证.纵观初中三年数学教材，还能发现不少“特殊关联”的“蛛丝马迹”.比如，平行四边形和梯形、矩形和直角梯形、等腰三角形和等腰梯形等.从这个意义出发，直角三角形和矩形、等腰三角形和菱形、等腰直角三角形和正方形也是“特殊关联”的.

值得一提的是，基于“特殊关联”的视角理解数学教材，不仅能为数学结论的探索与证明带来有益启示，也可以为数学例、习题的拓展延伸教学，乃至为中考数学命题开辟广阔思路.  3  结束语

通过以上论述，我们不难发现，基于思维生长的视角理解数学教材，同一知识系统的课程内容往往会遵循数学知识逻辑、思维生长逻辑和教材编排逻辑分布于不同的章节之中，随着学生对数学知识学习、理解的不断深入，一个个结论才会适时引入并加以呈现.上文所述前五个版本的数学教材均对直角三角形的性质与判定的有关内容作了类似的“分散”处理;多数版本的初中数学教材对一次函数与二次函数、全等三角形和相似三角形等内容的“分散”安排也是基于这样的考虑.

基于知识系统的视角，尤其关注对结构化的数学知识体系的构建.若由此视角审视、理解数学教材，在探索、证明出“直角三角形斜边上的中线等于斜边的一半”这一定理后不应就此止步，实际教学中还可继续启发学生进行如下思考：这个定理的逆命题是什么？此逆命题是真命题吗？如果是真命题，又该如何证明？这是因为，直角三角形的其他两个性质定理（直角三角形的两个锐角互余，勾股定理）以及“在直角三角形中，30°角所对的直角边等于斜边的一半”这一定理的逆命题都是真命题，所以在得到“直角三角形斜边上的中线等于斜边的一半”这一定理后，唯有进一步探讨其逆命题的真假（即便其逆命题未在数学教材中以定理的形式呈现），才算真正构建了完整意义上的“直角三角形的性质和判定”的知识系统，并实现了该系统的“闭环”.同时，我们还会欣喜地发现：随着学习的深入，以后还可根据圆周角定理的推论（90°的圆周角所对的弦是直径，半圆或直径所对的圆周角是直角）对“直角三角形斜边上的中线等于斜边的一半”这一定理及其逆命题作简洁而直观地证明.如此，不仅帮助学生拓宽了命题证明的思路，实现了数学思维的又一次生长，也进一步扩充、完善了“直角三角形”的知识系统，可谓一举三得.

参考文献

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.4：65-66，85.

[2] 吴之季，苏淳.义务教育教科书·数学（八年级下册）[M].上海：上海科学技术出版社，2013.11：87.

[3] 展涛.义务教育教科书·数学（八年级下册）[M].青岛：青岛出版社，2013.6：19.

[4] 人民教育出版社，课程教材研究所，中学数学课程教材研究所开发中心.义务教育教科书·数学（八年级下册）[M].北京：人民教育出版社，2013.9：53.

[5] 北京教育科学研究院.义务教育教科书·数学（八年级下册）[M].北京：北京出版社，2013：63.

[6] 马复.义务教育教科书·数学（九年级上册）[M].北京：北京师范大学出版社，2014.6：12.

[7] 严士健，黄楚芳.义务教育教科书·数学（八年级下册）[M].长沙：湖南教育出版社，2013.11：3.

[8] 杨俊英.义务教育教科書·数学（八年级上册）[M].石家庄：河北教育出版社，2013.7：147.

[9] 范良火.义务教育教科书·数学（八年级上册）[M].杭州：浙江教育出版社，2013：68.

[10] 王建磐.义务教育教科书·数学（九年级上册）[M].上海：华东师范大学出版社，2014.6：102.

[11] 杨裕前，董林伟.义务教育教科书·数学（八年级上册）[M].南京：江苏凤凰科学技术出版社，2013.6：65.

[12] 卜以楼.生长数学教学概论[M].西安：陕西师范大学出版总社，2022.3：259.

[13] 孙维刚.孙维刚初中数学[M].北京：北京大学出版社，2005.1：4.