多解提升思维，改编挖掘价值

梁亮亮

[摘  要] 广东省2021年学业水平考试的数学卷第23题是一道以正方形为背景的几何小综合题，考查的知识较多，包括正方形的性质、三角形全等的判定和性质、相似的证明和性质、勾股定理、等腰三角形的性质等，题目的解法多样，可以从多个角度去研究. 文章从题目的解法入手，并对题目进行改编，力求提升学生的思维，挖掘题目的教学价值.

[关键词] 一题多解;改编创新;教学运用;中考试题

原题呈现

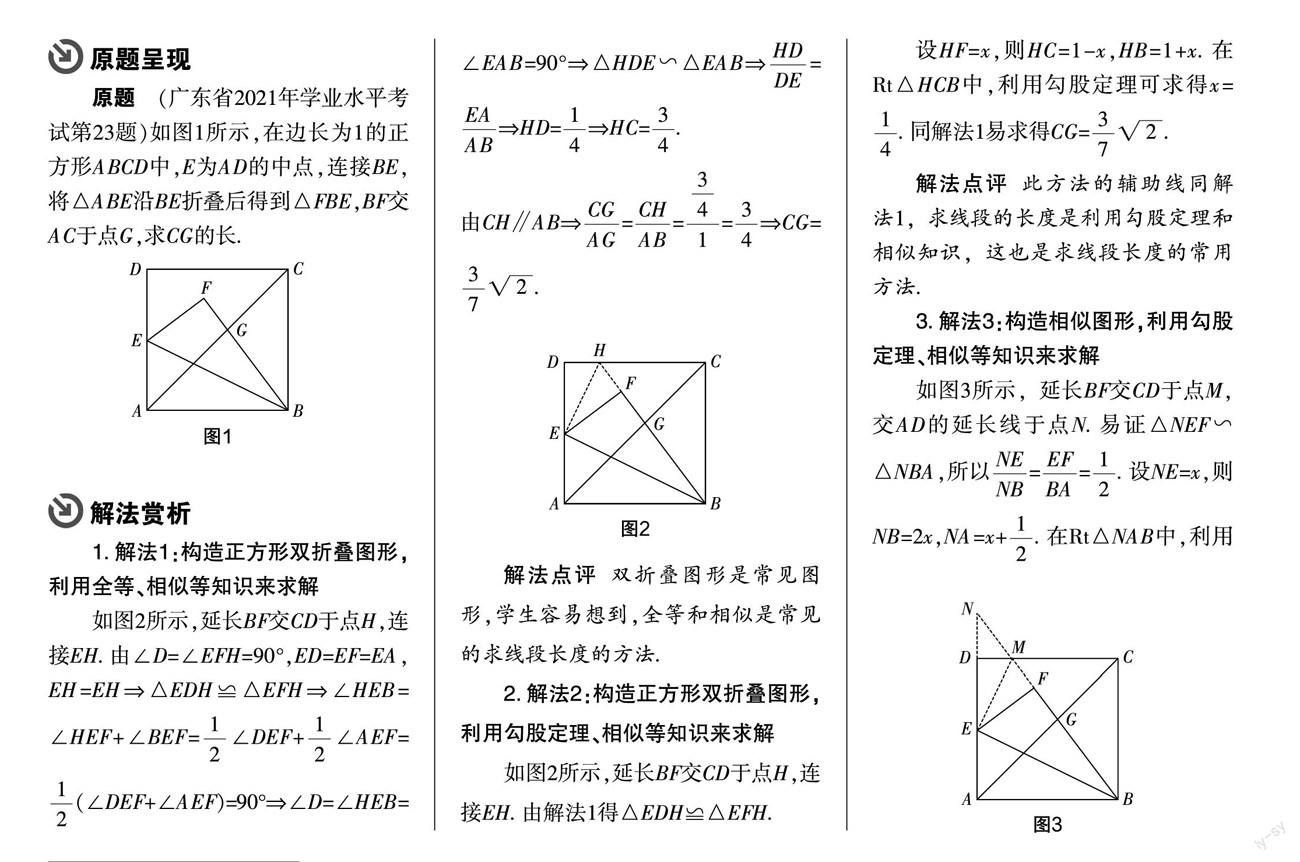
原题（广东省2021年学业水平考试第23题）如图1所示，在边长为1的正方形ABCD中，E为AD的中点，连接BE，将△ABE沿BE折叠后得到△FBE，BF交AC于点G，求CG的长.

解法赏析

1. 解法1：构造正方形双折叠图形，利用全等、相似等知识来求解

如图2所示，延长BF交CD于点H，连接EH. 由∠D=∠EFH=90°，ED=EF=EA，EH=EH?△EDH≌△EFH?∠HEB=∠HEF+∠BEF=∠DEF+∠AEF=（∠DEF+∠AEF）=90°?∠D=∠HEB=∠EAB=90°?△HDE∽△EAB?=?HD=?HC=.

由CH∥AB?===?CG=.

解法点评双折叠图形是常见图形，学生容易想到，全等和相似是常见的求线段长度的方法.

2. 解法2：构造正方形双折叠图形，利用勾股定理、相似等知识来求解

如图2所示，延长BF交CD于点H，连接EH. 由解法1得△EDH≌△EFH.

设HF=x，则HC=1-x，HB=1+x. 在Rt△HCB中，利用勾股定理可求得x=. 同解法1易求得CG=.

解法点评此方法的辅助线同解法1，求线段的长度是利用勾股定理和相似知识，这也是求线段长度的常用方法.

3. 解法3：构造相似图形，利用勾股定理、相似等知识来求解

如图3所示，延长BF交CD于点M，交AD的延长线于点N. 易证△NEF∽△NBA，所以==. 设NE=x，则NB=2x，NA=x+. 在Rt△NAB中，利用勾股定理可求得x=（舍去负值）. 则NA=. 利用△NAG∽△BCG，可求得CG=.

解法点评此解法需要学生能构造出相似图形，再利用勾股定理、相似知识来求线段的长度，辅助线的作法也是常见方法.

4. 解法4：构造直角三角形，利用角平分线的性质、相似、勾股定理等知识来求解

如图4所示，过点G作GH⊥BC，垂足为H，作GN⊥AB，垂足为N，GN交EB于点M. 设NB=x，则GN=AN=1-x，MN=x，GM=1-x. 由=，可求得GB=2-3x. 在Rt△GNB中，利用勾股定理，可求得x=（舍去x=1），所以GH=. 所以CG=.

解法点评此解法需要学生利用角平分线的性质，再利用相似、勾股定理等知识来求线段的长度，解法不容易想到.

5. 解法5：构造“一线三直角”模型，利用矩形性质、相似等知识来求解

如图5所示，过点F作CD的平行线，交AD于点H，交BC于点M，交AC于点N. 易证△EHF∽△FMB，于是有===. 设EH=x，则HA=+x，FM=2x，HF=1-2x，MB=2-4x. 由HA=MB，易求得EH=，MB=，HF=. 于是可得CM=NM=，FN=HM-HF-NM=. 由FN∥AB，易得△FNG∽△BAG， 所以==. 由NC=，AC=，易得NG=，从而求得CG=.

解法点评此解法需要学生构造出“一线三直角”模型，再利用相似知识来求线段的长度，辅助线比较难想到，解法也较难.

6. 解法6：构造全等、相似图形，利用全等的性质、相似等知识来求解

如图6所示，设AC与BE交于点H，连接FH，由△EAH∽△BCH，易得=，进而可推出AH=，HC=. 易证HF=AH=，∠GFH=∠BAH=∠GCB=45°， 从而可推出△GFH∽△GCB，于是得到==， 即==， 可求得CG=.

解法点评此解法需要学生运用两次相似知识，解法不容易想到.

7. 解法7：建立适当的平面直角坐标系，利用两点间的距离公式来求解

如图7所示，以A为原点，构造平面直角坐标系，则A（0，0），B（1，0），C（1，1），E（0，0.5）. 设F（a，b），则由两点间的距离公式可得EF==0.5，FB==1.于是可求得F

，

，直线FB的解析式为y= -x+. 再结合直线AC的解析式y=x，可求出G

，

，于是可求得CG=.

解法点评此解法需要学生建立适当的平面直角坐标系，并会用两点间的距离公式，对学生的能力要求较高.

8. 解法8：建立适当的平面直角坐标系，利用相似、解析法等知识来求解

如图8所示，过点F作CD的平行线，交AD于点H，交BC于点M. 参照解法5，易求得点F的坐标为

，，进一步可求得CG=.

解法点评此解法需要学生建立适当的平面直角坐标系，并会用解析法进行解决，对学生的能力要求较高.

上述解法，解法1到解法6都是构造相似图形，利用相似知识来求解;解法7和解法8则通过建立适当的平面直角坐标系，用解析法来求解. 本题还可以尝试利用三角函数的倍角公式来求解，但超出了初中生的知识范畴，故这里不做解析.

幾点思考

1. 从命题的角度：挖掘题目的价值

本题是几何小综合题，考查的知识较多，包括正方形的性质、三角形全等的判定和性质、相似的证明和性质、勾股定理、等腰三角形的性质等，考查的数学思想方法有转化、数形结合等，综合考查了学生的能力，难度较大.

题目条件较简洁，图形明了，观察图形后发现CG不在特殊的三角形中，图中没有包含CG的相似图形，也难以求出AG的长，所以不能利用现有的图形直接求出CG的长度，需要作辅助线，但辅助线如何作，是本题考查的难点.

从学生的答题情况来看，本题某市的平均分仅为0.5分，难度系数为6.25%，近95%的学生得0分或1分（超60%的学生得0分），可想本题的难度. 学生不能得分的原因主要是本题的入口较难，不会作辅助线，无从下手. 为了便于日常教学，笔者尝试对本题进行如下改编.

改编1如图9所示，在边长为1的正方形ABCD中，E为AD的中点，连接BE，将△ABE沿BE折叠后得到△FBE，BF交AC于点G，BF的延长线交CD于点H，连接EH.

（1）证明：∠HEB=90°;

（2）求CG的长.

改编2如图10所示，四边形ABCD为矩形，E为AD的中点，AD=4，AB=3，连接BE，将△ABE沿BE折叠后得到△FBE，BF交AC于点G，BF的延长线交CD于点H，连接EH.

（1）证明：∠HEB=90°;

（2）求CG的长.

改编意图上述改编不需要学生作辅助线，降低了入口的难度，让学生可以动笔;将一个小问拆成了两个小问，降低了本题的整体难度，便于学生日常训练.

2. 从教学的角度：落实怎么想，注重基础，强化思想

（1）落实怎样想

在几何解题教学中，教师既要教会学生怎样做，又要教会学生怎样想，做到授人以渔. 教学中，教师可选择一些有意义且难度不大的问题，通过一题多解，向学生展示分析问题之道，让学生学会思考和分析，在选择解题方向时不再盲目.

（2）注重基础

在分析和解决原题的过程中，我们发现原题涉及正方形的性质、全等、相似、勾股定理等基本知识. 对历年的中考难题进行分解后我们发现，它们都是由基本问题、基本图形通过变换、组合而形成的，因此，在平时的教学中，教师要高度重视基础知识和基本内容的落实.

（3）强化思想

解决原题用到了转化、数形结合等思想方法，其中转化思想方法是应用最广泛的数学思想方法之一，将未知量转化为已知量是破题之法. 在教学中，教师应有意识地向学生渗透转化思想，这样能提高学生分析问题的能力. 除此之外，模型、化归、类比等思想方法，是附著于数学课程内容而存在的，因此在平时的教学中教师可以有意识地渗透各种数学思想，以培养和提升学生的思维能力.