在数学文化体验中达成教学目标

曾磊磊

[摘  要] 数学文化可以加深学生对数学历史的了解，感受数学的魅力，体会追求真理的科学精神，鼓舞学生在学习数学的道路上不断探索，激发学生坚持长期学习和终生学习.

[关键词] 数学文化;核心素养;教学目标

数学文化是一个人数学核心素养的集中体现，它包括了数学思想、方法以及数学的形成和发展过程. 在中学阶段的教学过程中，教师往往会忽视数学文化，而看重解题训练，实际上这是本末倒置的做法. 新课程改革以来强调以培养学生的核心素养为目标，也就是强调数学文化的影响，通过数学知识和技能的学习，最终要使学生能形成数学思想，感受数学文化，才能真正爱上数学. 数学的魅力远远不在于会解试卷上的一道题，而是在数学文化的体验中能体会到多角度地看待问题，在探索發现中找寻真理的愉悦，达到学习的效果. 本文以“三角形的内角和”为例，谈一谈如何在体验数学文化中实现教学目标.

从基本拼图法，追溯定理起源

在学习了三角形的基本概念及其性质之后需要探讨三角形的内角和是多少，探讨这一问题的方法非常多，最基本的可以采用度量推理的方法，也可以采用剪拼验证的方法证明三角形的内角和为180°. 学生在动手实践的过程中既培养了操作实践的能力，也能发挥自己的创意，调动学习的积极性. 在引导学生探究的过程中，可以结合数学文化的发展过程，加深学生的印象.

案例1  拼图.

师：请大家准备六个全等三角形，试着拼一拼，能不能算出三角形的内角和是多少？

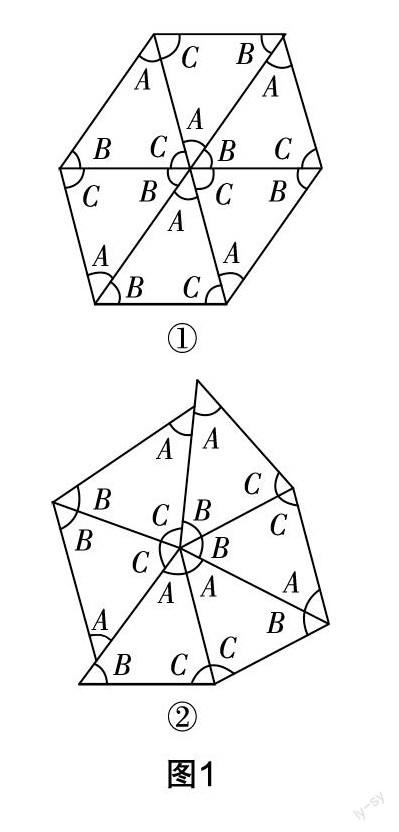
生：我把六个三角形拼在一起，让它们的顶角靠在一起.

师：是不是像图1所示的样子.

生：是的. 这样六个顶角就拼成了一个周角，也就是360°，而每个三角形的顶角出现了2次，也就是2∠A+2∠B+2∠C=360°，那么∠A+∠B+∠C=180°，也就是三角形的内角和.

师：同学们很厉害，这是一个发现三角形内角和定理非常好的方法，而且同学们知道吗？这个方法早在古代就有数学家使用过，他就是古希腊的数学家泰勒斯，他和大家一样就是通过三角形拼图发现了三角形的内角和定理. 看来同学们都是数学家！

本例中教师引导学生通过自己动手拼图的方式发现三角形的内角和，知道三角形的内角和并不难，教师在这里将学生们的方法与古代数学家的方法相比较，让学生感受到数学定理的发现并不是不能想象的，鼓舞了学生学习数学的信心，并且发现数学方法的过程又充满了趣味，激发了学生探究的乐趣.

优化拼图法，掌握定理

学生在感受到初步获得数学成果的成就感之后，可以进一步鼓励学生向古代数学家发起挑战. 天生的竞争意识会让学生马上变得跃跃欲试，希望比数学家更厉害.

案例2  三个全等三角形拼图证明三角形内角和定理.

师：数学家泰勒斯发现三角形内角和定理当然非常了不起，但是在我们今天看来似乎他的方法有些烦琐，用的三角形有点多，同学们能不能挑战一下他的拼图方法，让这个过程更简便呢？

（学生跃跃欲试，积极行动起来. ）

生1：我知道了，刚才拼的图1，如果去掉上面一半，用三个三角形一样能拼出三角形的内角和为180°，看我拼成了这样（如图2所示）.

生2：我也可以用三个三角形拼，但是和生1的图形不一样（如图3所示）.

学生相继展示了如图4、图5所示的拼图效果.

师：你们真是太厉害了. 用三个全等三角形顶角不重合拼在一起，每个三角形的顶角用一次，刚好能拼成一个平角180°. 那你们真是比数学家泰勒斯还要了不起，他用六个全等三角形才拼出来，你们只用了三个全等三角形，过程更简便.

那么我们再继续观察一下图3、图4和图5，这三幅图有什么是相等的呢？

生3：这三幅图中有相等的内错角.

师：很好，观察很仔细，那么根据平行线的判定，我们就能找到图形中的平行线了. DE与BC平行，利用内错角相等，∠B和∠C就可以转移到上面A点的位置，由此就变成了一个平角，同样可以得到三角形的内角和定理.

教师总结：所以我们利用三个全等三角形同样可以找到一种非常简洁的方法，发现三角形的内角和定理，这也告诉我们科学的追求是无止境的，只要我们用科学的方法，坚持不懈，一定能发现其中的奥秘.

本例中教师通过鼓励学生挑战的办法，让学生去发现新的研究方法，培养了学生的创新意识. 并且逐渐渗透了通过作辅助线的办法也可以论证三角形的内角和定理，为之后的几何证明题打下基础. 在教学中教师的引导和突破帮助学生拓宽了视野，更新了学习方法，潜移默化地陶冶了学生的数学思想，可谓一举多得.

拓展思维，难度升级

学生在进行了一轮挑战之后信心满满，此时教师可以趁热打铁，进行难度升级，进一步去发散学生的思维，感受数学追求的乐趣.

案例3  一个三角形证明三角形内角和定理.

师：刚才我们已经尝试了用六个全等三角形和三个全等三角形证明三角形的内角和定理，老师觉得可以难度升级，用一个三角形来证明三角形的内角和为180°. 你们愿意尝试一下吗？

（有的学生有点犹豫，觉得不可能实现，有的学生被激发起挑战的欲望，教师可以进一步鼓励. ）

师：我觉得同学们有巨大的潜力，可以完成这个艰巨的任务.

（学生纷纷开始思考，有的几位同学窃窃私语的讨论，有的同学开始拿出纸进行折叠. 学生发现一个三角形是无法拼图的，那就进行折叠. ）

生1：我发现了一种折叠方法. 我一边画一边说，先把上面的三角形往下折叠，与下面的边相交，再把两边的三角形向内折叠，这样三个三角形拼在了一起，组成了一个平角（如图6所示），可以证明三角形的内角和为180°.

师：非常巧妙的方法，很厉害.

生2：我有另外一种方法. 我通过把三角形的三个角作角平分线的方式，让它们相交于一点，三角形的三个角对准交点进行折叠，三个角和它们的对顶角在一起组成了一个周角，同样可以证明三角形的内角和是180°（如图7所示）.

师：同学们的方法非常厲害，那事实上大家的方法早在历史上被一个12岁的小男孩发现过. 这个小男孩就是法国著名的数学家、哲学家、物理学家帕斯卡，他在12岁时独立地利用对称证明了三角形的内角和定理. （学生发出赞叹. ）他的父亲和同学们一样非常惊喜，此后允许他阅读任何数学书籍，当然他用成就说明了他在数学上的天赋和造诣. 那么，你们还有没有其他的方法呢？

生3：我是用了一个添补的方法，在AB和AC边的中点对BC边作垂线，然后沿垂线把两个三角形剪下来，补到上面成为一个长方形，同样三角形的三个内角组成一个平角，证明了三角形的内角和为180°（如图9所示）.

在教师的引导下学生的思维不断进阶，从三个三角形到一个三角形，从折叠到剪拼，学生的思维得到了发展，视野不断拓宽，不仅提升了学生的数学学习力，而且提升了学生的核心素养.

创新思维，不拼也不折

学生通过从六个全等三角形到三个全等三角形直到一个三角形，难度不断升级，但是学生都找到了突破的方法. 那么上面采用的都是拼和折的方法，能不能在证明方法上有所突破呢？

师：刚才同学们的方法都很好，那么现在我们想用一个更加简便的方法，不拼也不折，用一支笔的旋转能不能有所突破呢？

（学生表示出很困惑. 教师进行指导，师生共同交流得到答案. ）

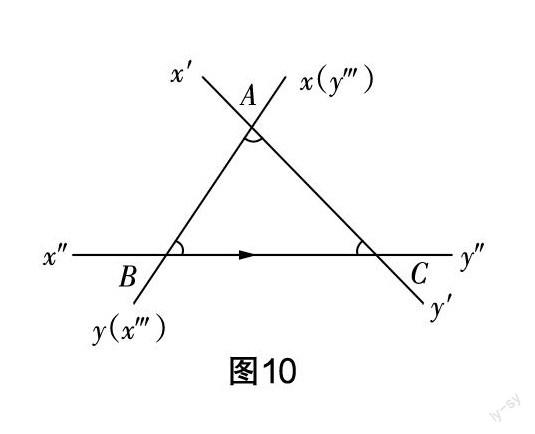
师：同学们看这幅图（如图10所示），一支笔如BC绕点B进行旋转，到达BA，再绕点A逆时针旋转与AC重合，再沿点C逆时针旋转与CB重合，这样笔尖回到原位经历了180°，也证明了三角形的内角和定理.

这是德国数学家提波特1809年发现的证明方法，通过直线旋转的方式，旋转180°，由此证明了三角形的内角和为180°. 通过引导学生不断地深入思考，发现三角形内角和的证明方法，体会数学文化，感受数学魅力. 学生如同数学家一样不断地有创新的发现，激发了学生学习的主动性和积极性.

学生通过自己的操作实践，采用拼、剪、折等方式去论证自己的推理，在过程中感受知识的获得，有效地培养了学生的思维深刻性，也使学生能将情感态度、价值观与知识学习融为一体，不断提升数学核心素养.