反思性学习,让学生“学会学习”

张婷

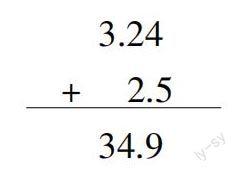
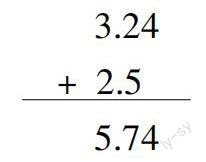
[摘  要] 通过数学反思性学习，能够优化学生思维结构，启发学生数学智慧，让学生学会学习，从而助力学生未来发展。基于教学实践，文章提出在小学数学课堂贯彻落实反思性学习的基本策略，即引发认知冲突，激发反思意识;把握适切问题，提供反思空间;追溯学习过程，提升反思能力。

[关键词] 反思性;意识;小学数学

荷兰数学教育家弗赖登塔尔说：“反思是数学思维的核心和动力。”反思就是通过思考过去的经历，总结成功的经验和失败的教训，简而言之，反思就是对过去经历的再认识。就小学数学的学科特点来看，数学的学习过程不仅是一个思考的过程，更是一个不断反思自己思维活动的过程。通过数学反思性学习，能够优化学生思维结构，启发学生数学智慧，让学生学会学习，从而助力学生未来发展。本文从三个角度论述了在小学数学课堂贯彻落实反思性学习的基本策略，力图为优化学生思维品质，为提升学生思维智慧提供更具针对性的建议。

[?]一、引发认知冲突，激发反思意识

反思的过程实际上就是学生自我意识觉醒的过程，也是学生对自己学习过程的自我否定和再认识。所以，教学中教师要引导学生关注自己的思维过程，促使学生对自己的认知方式和思维结构进行批判性的认识和思考。这就要求教师要从学生的认知水平和生活实际出发，创设情境，引发学生新旧知识之间的冲突，引发学生对学习方法、解题思路和情感体验进行反思，追溯思维路径，发现思维盲点，从而使学生的思维具有深刻性和批判性[1]。

比如“小数的加法”教学节选。

师：请同学们计算3.24+2.5。

生1：这是我的计算结果。

3.24

+  2.5

34.9

生2：我认为他的计算结果不对。小数加法应该把小数点对齐。

3.24

+ 2.5

5.74

生1：我们在整数的加法计算时，都是把数字的末位对齐，为什么现在把末位对齐就不对了呢？

生2：如果把数字的末位对齐，就不是相同数位相加了。比如，你的竖式就是把第一个加数的百分位和第二个加数的十分位相加，把第一个加数的十分位和第二个加数的个位相加，这显然是不对的。

生1：哦，我懂了。如果把末位对齐就不能保证相同数位相加了。看来整数加法的末位对齐和小数加法的小数点对齐并不相同啊！

师：大家如何看待整数加法的末位对齐和小数加法的小数点对齐呢？

生3：我认为这两种对齐方式在本质上并没有差别。

生2：完全不一样嘛，怎么会没有差别呢？（同学间相互议论）

生3：整数加法的末位对齐是为了保证相同数位相加，而小数加法的小数点对齐也是为了保证相同数位相加，这一点上它们不是完全相同的吗？

师：生3的分析非常精彩。尽管对齐的具体形式不同，但是它们的目的都是一样的，就是为了保证相同数位相加。

师：那么，请问生1，你认为自己在思考中有什么不足呢？

生1：我没有注意到相同数位相加这个原则，所以导致计算过程和结果都出现了失误。

生2：尽管我意识到了小数加法要把小数点对齐，但是我认为小数加法的小数点对齐和整数加法的末位对齐完全不同。

师：生3既意识到了小数点对齐和末位对齐在形式上的差别，也意识到了二者在本质上的一致性，可见他对整数加法和小数加法的认识是深刻的，请同学们向他学习！

引发学生认知冲突是促使学生进行反思的有效手段。教学中，生1按照整数加法的方法计算小数加法，导致结算结果错误，由于新知識与旧知识产生了认知上的矛盾，这种思维冲突引发了学生对自己的思维过程进行反思。生1、生2和生3的思维层次具有比较明显的差异，生1的思维层次处在“不知其然”的初级层次，生2的思维处在“知其然，不知其所以然”的中级层次，生3的思维处在“知其然，知其所以然”的高级层次，教师通过引导学生对自己的思考历程进行回顾和反思，不但使学生发现了自己做错的原因，还找到了自己的思维“瓶颈”，优化了自身的思维结构，提升了思维品质。

[?]二、把握适切问题，提供反思空间

教学中，教师要把握适切问题，为学生反思提供更广阔的维度和空间。学生通过反思自己解决问题的过程，找出问题的核心，感悟自己方法的独特之处和不足之处，从而达到优化思维结构的目的[2]。

比如“两三位数的加法与减法”教学节选。

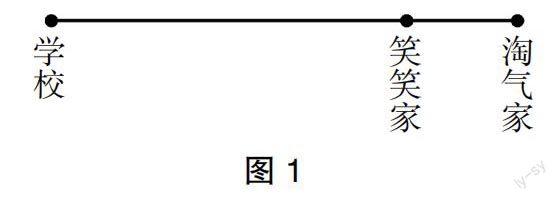
师：淘气家、笑笑家和学校在一条大街上。淘气家到学校的距离是200米，笑笑家到学校的距离是150米，那么，淘气家到笑笑家的距离是多少米？

生4：这个问题不难。200-150=50（米）。

师：你能说一下你的解题思路吗？

生4：200-150表示淘气家到学校的距离减去笑笑家到学校的距离，结果就是淘气家到笑笑家的距离，如图1所示。

生（众）：不错，我也是这么计算的。

师：同学们都是这样想的吗？

生5：我有不同的算法。生4计算的结果没有错，但是只包含了其中的一种情况，还有另一种情况，如图2所示。

生5：当淘气家和笑笑家分别在学校的两侧时，淘气家到笑笑家的距离就应该是200+150=350（米）。

师：同学们是如何看待自己解题过程的呢？

生4：我只考虑了其中的一种情况，想问题不全面，只考虑到淘气家和笑笑家都在学校一侧，没有考虑到淘气家和笑笑家也有可能在学校的两侧。

师：我们只有准确了解了自己在思维上有哪些不足，才能更好地优化我们的思维。

从整体上看，教学中的题目难度并不大，却是考查学生数学思维严密性的生动素材。生5的思维缜密性显然要优于生4，生4通过对自身解答过程的反思，意识到了自己在解答思路的不足之处，从而为进一步优化思维结构提供了方向，由此凸显了反思性学习的重要价值。

[?]三、追溯学习过程，提升反思能力

由于年龄特征和认知特点，小学生对知识的掌握往往呈现出“碎片化”状态，当学生掌握零散的知识后，若教师再引导学生对相关知识进行系统回顾和反思，这些看似“一盘散沙”的知识就会慢慢地聚合起来，形成一个相对完整的认知体系。因此，在数学教学中，当新授课或者某一专题知识宣告结束时，教师要引导学生“回头看”，对新知探究过程或者相关知识之间的内在联系进行回望和反思，追溯学习过程，梳理新旧知识联系，最终形成完整的认知结构[3]。

比如讲到“圆的面积”后，教师引导学生对探究过程进行了系统反思。

师：同学们，我们现在已经推导出了圆的面积公式。那么，谁能说说圆的面积公式是怎样推导出来的呢？

生6：我们把圆转化成了平行四边形，由此推导出了圆的面积公式。

师：圆的面积推导过程，让你想起了我们以前学过的哪些知识呢？

生6：我想起了我们学过的平行四边形面积、三角形面积和梯形面积。这3种图形的面积推导过程跟我们这节课的内容很像。

师：它们有哪些相同点呢？

生7：它们都用到了转化思想。

师：是如何具体用到转化思想的呢？

生7：我们把平行四边形转化成长方形，由此推导出了平行四边形面积公式;我们把三角形转化成平行四边形，由此推导出了三角形面积公式;我们把梯形转化成平行四边形，由此推导出了梯形面积公式;这节课我们把圆转化成平行四边形，又推导出了圆的面积公式。

师：看来我们用到转化思想的地方还真不少呢！除了转化思想，这些知识还有什么关联？

生8：我们推导这几个图形面积公式的过程也都相同。首先完成图形的拼接和转化，其次分析新图形与原图形的关系，最后推导出图形的面积公式。

教学中，教师引导学生对“圆的面积”学习过程进行回顾和反思，主要产生了3个作用：一是加深了对新知识的理解。通过回顾圆的面积公式推导过程，进一步加深了学生对新知识的理解深度，使新知识在学生脑海中的印象更加稳固。二是把新旧知识有效地联系起来，形成完整的认知体系。圆的面积与学生学习过的平行四边形、三角形等图形面積是一脉相承的，把圆的面积纳入学生已有的认知体系，有利于学生形成系统化知识。三是深刻领悟了转化思想，掌握了推导几何图形面积公式的一般步骤和方法。数学思想是数学的灵魂。但是，学生感悟数学思想需要反复体验，教师通过引导学生进行回顾和反思，使学生意识到了转化思想在数学学习中的重要作用，掌握了推导几何图形面积公式的基本方法，为下一步学生推导圆柱体积打下了坚实的理论基础和思想基础。

“思之则活，思活则深，思深则透，思透则明，思明则新，思新则进”，反思教学的最终目的是使学生学会学习，它既关注学生学习的结果也注重学生思考的过程，既着眼学生的当下也兼顾学生的长远发展。因此，教师要在教学中有意识地引导学生对学习过程进行回望和反思，使学生总结成功的经验、吸取失败的教训，学生的思维结构就会不断地得到优化，从而促进学生学习能力的提升。

参考文献：

[1]  王红娟. 反思，让学习更有深度——小学数学教学引导学生进行反思性学习的研究报告[J]. 教育观察，2020，9（15）：8-9+20.

[2]  林慧. 小学课堂反思性学习的应用探寻[J]. 内蒙古教育，2019（23）：84-85.

[3]  胡红. 反思性学习，让数学学习走向深度[J].小学教学参考，2019（08）：90-91.