概率也生长计算有新法

曹小兵 崔恒刘

生活中的事件有许许多多的不确定性。八（下）“认识概率”从概率的统计定义出发，展开了对概率初步知识的研究，得到了计算随机事件的概率的方法，即在一定的条件下，以试验的客观对称性或均衡性为前提，进行概率的计算。这需要解决两个问题：一是如何判断试验结果的等可能性；二是在等可能条件下，用哪些方法计算简单随机事件的概率。为此，九（上）“等可能条件下的概率”安排了3节内容来解决这两个问题。

第1节，以熟悉的实例为问题背景，帮助我们理解随机试验的所有可能结果，进一步理解等可能的意义，学会根据随机试验结果的客观对称性或均衡性判断试验结果是否具有等可能性，归纳出等可能性事件的两个基本特征：一是试验所有可能出现的结果是有限个；二是每一个试验结果出现的可能性相同。

例1 两个正四面体骰子的各个面上分别标明数字1、2、3、4，如果同时抛掷这两个正四面体骰子，则着地面所得的点数之和是2和5，它们是等可能的吗？

【解析】很多同学会觉得，着地面所得的点数之和分别是2、3、4、5、6、7、8，共有7种不同的结果，是等可能结果。不过，着地面点数之和是2、3、4、5、6、7、8不假，但结果不是等可能的。我们可以有序思考（为便于说明，我们将两枚正四面体骰子分别记作骰子A和骰子B）：

如果骰子A抛出1，骰子B可能是1、2、3、4，对应的和分别为2、3、4、5；

如果骰子A抛出2，骰子B可能是1、2、3、4，对应的和分别为3、4、5、6；

如果骰子A抛出3，骰子B可能是1、2、3、4，对应的和分别为4、5、6、7；

如果骰子A抛出4，骰子B可能是1、2、3、4，对应的和分别为5、6、7、8。

由此看出，共有16种情况，着地面所得的点数之和等于2的结果只有一种，等于3的共有2种，等于4的共有3种，等于5的共有4种，等于6的共有3种，等于7的共有2种，等于8的共有1种，它们不是等可能的。

第2节，通过具体的问题情境，在理解等可能事件的两个基本特征的基础上，归纳出等可能条件下概率（古典概率）的计算公式：

P（A）=[事件A发生可能出现的结果数m所有等可能出现的结果数n]。

例2 甲口袋装有编号为1、2的两个球，乙口袋装有编号为1、2、3、4、5的五个球，两个口袋中的球除编号外都相同。小冰先从甲口袋中随机摸出一个球，小雪再从乙口袋中随机摸出一个球，若两球编号之和为奇数，则小冰获胜；若两球编号之和为偶数，则小雪获胜。

请用列表或画树状图的方法，说明这个游戏对双方是否公平。

【解析】列表，所有可能的结果如下：

共有10种等可能的结果，其中两球编号之和为奇數的有5种结果，两球编号之和为偶数的有5种结果， 所以P（小冰获胜）=5/10=1/2，P（小雪获胜）=5/10=1/2。

因为P（小冰获胜）=P（小雪获胜），所以游戏对双方都公平。

【点评】判断游戏的公平性需要先计算每个事件的概率，然后比较概率的大小，概率相等就公平，否则就不公平。

第3节，运用“无限”向“有限”转化的思想，将“等可能条件下的概率（二）——几何概型” 转化为“等可能条件下的概率（一）——古典概型”来研究解决，试验的取值范围从正整数推广到正实数，试验的结果从“有限”推广到“无限”。

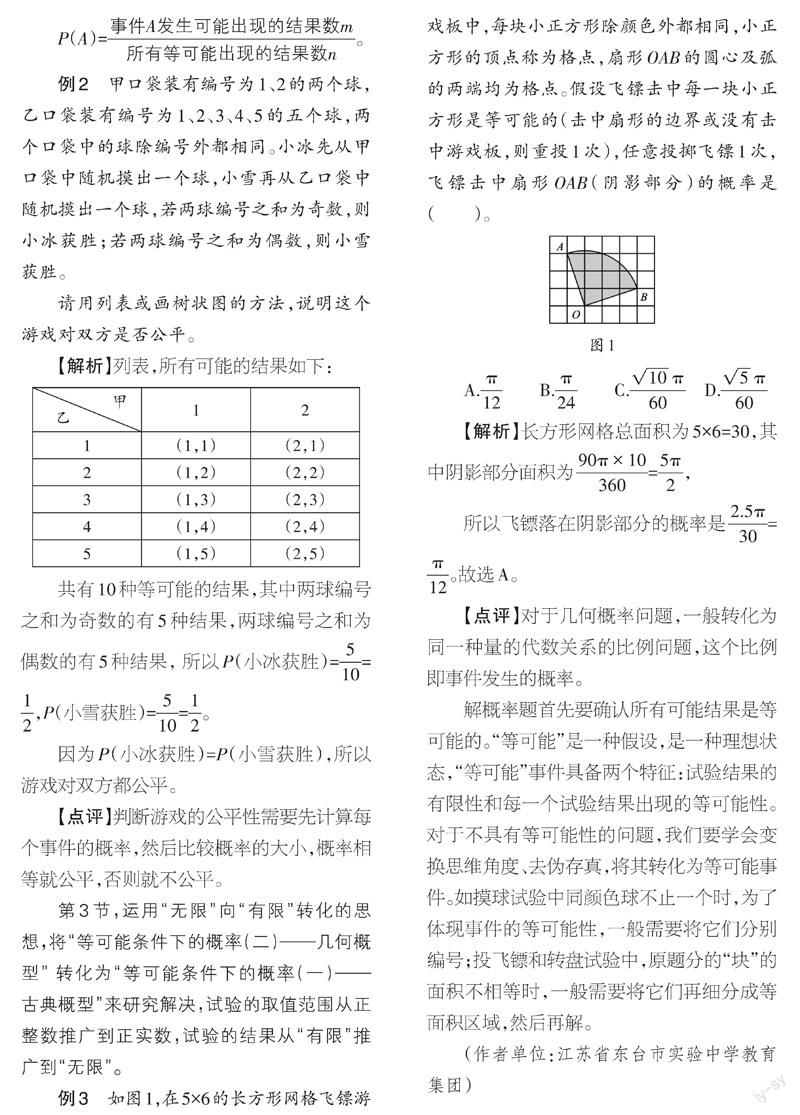
例3 如图1，在5×6的长方形网格飞镖游戏板中，每块小正方形除颜色外都相同，小正方形的顶点称为格点，扇形OAB的圆心及弧的两端均为格点。假设飞镖击中每一块小正方形是等可能的（击中扇形的边界或没有击中游戏板，则重投1次），任意投掷飞镖1次，飞镖击中扇形OAB（阴影部分）的概率是（ ）。

A.π/12 B.π/24 C.10π/60 D.5π/60

【解析】长方形网格总面积为5×6=30，其中阴影部分面积为[90π×10360]=[5π2]，

所以飞镖落在阴影部分的概率是2.5π/30=π/12。故选A。

【点评】对于几何概率问题，一般转化为同一种量的代数关系的比例问题，这个比例即事件发生的概率。

解概率题首先要确认所有可能结果是等可能的。“等可能”是一种假设，是一种理想状态，“等可能”事件具备两个特征：试验结果的有限性和每一个试验结果出现的等可能性。对于不具有等可能性的问题，我们要学会变换思维角度、去伪存真，将其转化为等可能事件。如摸球试验中同颜色球不止一个时，为了体现事件的等可能性，一般需要将它们分别编号；投飞镖和转盘试验中，原题分的“块”的面积不相等时，一般需要将它们再细分成等面积区域，然后再解。

（作者单位：江苏省东台市实验中学教育集团）