初三数学复习课中“微专题”构建策略
2022-05-30郭红如

[摘 要] 初三数学复习课中构建“微专题”教学可以有效提高数学复习课效率,研究者以“反比例函数”专题复习课为例,探讨了初三数学复习课中“微专题”教学的构建策略.
[关键词] 初三数学;复习课;微专题
认知负荷学习理论认为:工作记忆的容量是有限的,每次只能储存5~9条基本知识信息(或称为基本信息块),教育教学学习的知识信息经过工作记忆阶段加工后,主要储存在长时记忆中;如果需要加工的知识信息超过工作记忆的容量,就会造成学习者的认知负荷,学习者的学习多被认为是无用的[1]. “微专题”即小专题,“微”是指模式,“专”是指内容. 初三数学复习课中引入“微专题”复习,学习容量小且问题集中,目标明确容易理解,可以紧密联系相关的数学知识和方法,能有效降低学生的认知负荷,提高复习效率.
“微专题”复习课构建举例
(一)知识点回顾
构建新的活动认知,需要对概念和性质进行回顾,建立联系,抽象出简约的知识网络框架(如图1),发展学生的数学抽象能力.
(二)本节课内容要点
反比例函数y=(x≠0)中k值的求解.
原理:在反比例函数图像上,任意取一点向两坐标轴作垂线段,与两坐标轴所围成的四边形的面积为
k
.
(三)设置热身训练
关于反比例函数的概念、性质,教师带领学生进行回顾之后,再引出关于k值的求解,让学生简单说明为什么四边形的面积为
k
. 然后进行热身训练,学生通过训练更快地进入本节课主题,加强自身对xy=k(k≠0)这一函数形式的理解. “微专题”中热身训练习题的选择一定要体现基础性,让大部分学生能有所收获,使学生掌握利用函数基本概念和基本性质来解决问题的方法.
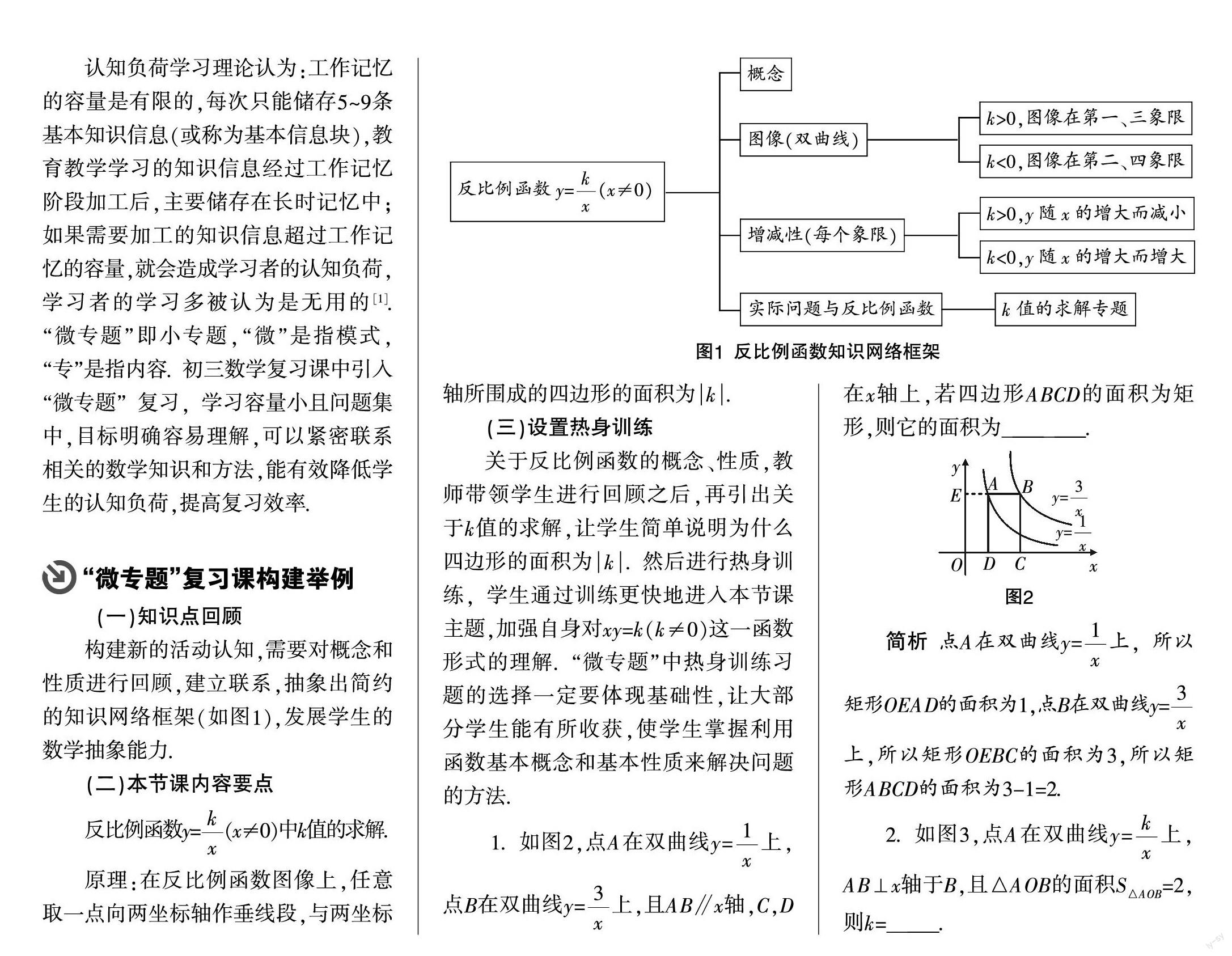
1. 如图2,点A在双曲线y=上,点B在双曲线y=上,且AB∥x轴,C,D在x轴上,若四边形ABCD的面积为矩形,则它的面积为________.
简析 点A在双曲线y=上,所以矩形OEAD的面积为1,点B在双曲线y=上,所以矩形OEBC的面积为3,所以矩形ABCD的面积为3-1=2.
2. 如图3,点A在双曲线y=上, AB⊥x轴于B,且△AOB的面积S=2,则k=_____.
简析 由反比例函数的图像特点可以判断k<0,三角形OAB 的面积等于,所以k=-4.
3. 如图4,点A,B是双曲线y=上的点,分别经过A,B两点向x轴、y轴作垂线段,若S=1,则S+S=________.
简析 点A,B在双曲线y=上 ,所以S+S+S+S=3+3=6,所以S+S=4.
说明 这类利用面积求k值的问题,要先根据反比例函数的图像特点去判定k的正负. 经过热身训练之后,学生对反比例函数k值求解问题有了比较明确的思路,可以掌握基本的解题技巧.
(四)设置拔高训练与变式演练
例1 如图5,已知双曲线 y=(k≠0),经过Rt△OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为______.
A. 12B. 9C. 6 D. 4
简析 由点A的坐标是(-6,4)可知,Rt△OAB的面积为12,点D的坐标为(-3,2),所以k=-6,所以△OBC的面积为3,所以S=S-S=12-3=9.
例2 如图6,反比例函数 y=(k≠0)的图像经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为_________.
简析 首先根据图像去判断k<0, OC=CD可知CE为Rt△ODB的中位线,四边形BDCE的面积等于S=×
k
=2,所以k=-.
说明 例题1与例题2依旧沿用热身训练的思路与方法,但问题中涉及三角形的个数有所增加,用到与三角形相关的一些性质,难度逐步提升.
例3 如图7,Rt△ABC的直角边BC在x轴正半轴上,D斜边AC边上的中点,连接BD并反向延长交y轴负半轴于E,双曲线 y=(x>0)的图像经过点A,若△BEC的面积为6,则k等于_______.
A. 3B. 6C. 12 D. 24
简析 先根据函数图像判断k>0, D是斜边AC边上的中点,BD=DC,进而根据角度关系判断Rt△ABC∽Rt△EOB,BO∶CB=EO∶AB,所以BO·AB=CB·EO,S=CB·EO=BO·AB,而BO·AB=k=6,所以k=12.
变式演练:如图8,Rt△ABC的直角边BC在x轴正半轴上,AC边上有一点使得AD∶DC=1∶2,BD反向延长线交y轴负半轴于E,双曲线 y=(x>0)的图像经过点A,若△BEC的面积为6,则k等于_____.
A. 3B. 6C. 12 D. 24
简析 如图9,由点D向x轴作垂线交x轴于点M,构造与Rt△ABC相似的Rt△DBM,同样利用Rt△EOB∽Rt△DMB可以得出k值.
说明 例题2与变式演练,利用看似跟图像不太相关的三角形的面积来解决问题,跟三角形有关的线段比例问题,很容易让人联想到相似三角形,利用相似三角形边长成比例,容易得到线段长度乘积,使问题得到解决.
关于复习课中“微专题”构建的三点思考
(一)概念引领,设置体现核心知识的基础练习,注重學生基础过关
所谓一般概念(big ideas)指的是与核心概念和理论相关的研究问题的一般套路[2]. 反比例函数这堂课的核心概念就是反比例函数定义,一般套路就是利用函数图像中面积与k值的关系来解决问题. 学生回顾相关理论知识后,需要进行一定的练习来达到知识点重构的目的. 课堂时间是一个不变量,在一定的时间获取更多的知识,需要学生不断探索提高复习效率的方法,所以在这个环节,教师一定要选择难度适中,能够体现本节课核心知识的练习题,使得大部分学生都能够过关.
(二)细节引领,设置难度合理分布的拔高练习,注重发展良好的思维品质
一节好的“微专题”复习课,训练的难度与广度一定是呈阶梯分布,当学生的学习热情逐步提高时,训练的难度可以适时提高,让学生感到一定的挑战性.同时,题后可适当设置一些变式演练.变式教学的使用,能够借助题目的变式照顾优等生和后进生,提高学生课堂互动的参与度[3].
另外,任何数学知识的学习都离不开数学运算,数学运算是数学六大核心素养之一. 重视运算的算理体现在解题的方方面面,运算的过程和结果也同样重要,所以“微专题”复习中,教师一定要重视学生的运算能力的培养. 同时,在涉及函数、方程等代数方面的知识点时,不可避免地会出现许多代数式和几何符号,教师在规范学生解题格式上一定要有所要求.
(三)思想引领,设置题后总结环节,注重学生经验积累
数学思想方法是基于实践经验积累的一种升华,而实践经验又需要不断总结、归纳与提炼[4]. “微专题”复习课的构建,要注重梳理和体现知识脉络,突出本节课的理论依据,牢牢抓住问题的解决原理. 此外,教师还需要及时进行题后的总结与错题的反思,理清典型问题的思路,总结典型问题的方法,抓住典型的错误进行分析,帮助学生积累經验,提高解决问题的能力.
结语
数学学习不应只有枯燥和乏味,在教育学生喜欢数学之前,数学教师首先自己要热爱数学,只有对数学教学充满热爱才能做好数学教学. 初三复习时间紧、任务重、难度大,构建有效的“微专题”复习课,需要广大教师不断探索和研究.
参考文献:
[1] 张慧,张定文,黄荣怀. 智能教育时代认知负荷理论发展、应用与展望——“第十一届国际认知负荷理论大会”综述[J]. 现代远程教育研究,2018(06):37-44.
[2] 吴增生. 整体建构核心素养导向下的总复习教学策略体系[J]. 中国数学教育,2019(Z3):3-11,37.
[3] 蒋炳强. 初中数学课堂师生互动有效性探索的实践研究[J]. 数学教学通讯,2018(35):28-29.
[4] 郭红如. 化碎为整,构建知识体系[J]. 中学数学教学参考,2020(15):68-69.
